感应耦合电能传输系统自持振荡控制

蓝建宇， 唐厚君， 耿欣

(上海交通大学，电力传输与功率变换控制教育部重点实验室，上海200240)

0 引言

无线电能传输技术可以不通过物理接触对电子设备供电。目前无线电能传输的方式有辐射式电能传输，磁谐振式电能传输和磁感应式电能传输3种方式［1］。辐射式电能传输方式传输距离远，但效率很低，传输功率也很小，功率等级为毫瓦级;磁谐振式电能传输为近五年发展起来的传输距离较大的电能传输方式，其技术还不是很成熟［2］。而感应式电能传输由于其传输功率大，效率较高一直是研究的热点。作为一种新型的电能传输技术，感应耦合电能传输(inductively coupled power transfer，ICPT)通过松耦合变压器把电能无接触地传输给负载，克服了传统导线式传输存在的裸露导体、接触火花等不安全因素［3－4］。ICPT系统广泛应用于喷漆车间、井下作业、电动汽车充电及生物医疗领域［5－8］。

松耦合变压器是ICPT系统能量传输的主要部件。与传统变压器不同的是，其初、次级绕组之间存在较大的气隙。因此，松耦合变压器的耦合系数低，漏感大。为了提高松耦合变压器的传输能力，通常在变压器的初级或次级增加补偿电容以构成谐振变换器［9－14］，补偿形式分为单边补偿和双边补偿，单边补偿一般为初级绕组补偿，双边补偿在初、次级绕组都接补偿电容。常见的双边补偿方式有PP、PS、SS和SP等。

ICPT系统双边补偿方式提高了电能的传输效率和功率，但同时引入了两个电容，增加了系统的阶数，这给ICPT系统带来不稳定因素，其中，频率分叉是较常见的问题［15－18］。文献［15］推导了在初级零相位角谐振频率下系统稳定运行时负载电阻的边界条件;文献［16］通过数学计算使谐振电容限定在一定范围而使系统不发生频率分叉。文献［15－16］都是通过参数设计的方法使系统只出现一个谐振频率点，从而不发生频率分叉，没有从根本上解决频率分叉的控制问题。文献［17］运用离散时间建模的方法对ICPT系统的频率分叉的稳定性展开研究。文献［18］针对CLC补偿型拓扑的频率不确定性建立系统的广义状态空间扰动模型并提出了鲁棒控制策略，但广义状态空间模型的建立相对复杂。

本文针对ICPT系统频率分叉现象展开研究，建立了SP补偿ICPT系统的自持振荡控制系统(selfsustain oscillation control，SSOC)。当系统发生频率分叉时，在SSOC控制器的作用下，通过频率自由振荡的方式趋于稳定。基于自持振荡控制的ICPT系统可以不用限定负载的范围，在系统轻载即发生频率分叉时也能保持输出电压的稳定。论文由以下部分组成，首先，建立了SP补偿ICPT系统的互感耦合模型，并分析了频率分叉时系统在变频控制下不稳定的原因。然后，基于描述函数法建立了ICPT系统的非线性模型并对发生频率分叉现象的ICPT系统进行稳定性分析。在此基础上将自持振荡控制器引入ICPT的控制中并与传统的变频控制进行对比分析。最后，实验验证了该方法的可行性。

1 ICPT系统建模

ICPT系统由逆变电路、松耦合变压器、补偿网络及整流电路组成，SP补偿方式的ICPT系统如图1所示。

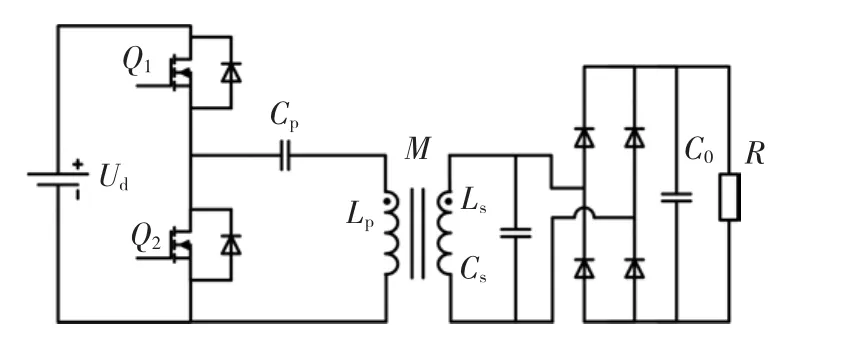
图1 SP补偿ICPT系统Fig.1 SP type compensation ICPT system

如图，半桥逆变电路产生高频方波电压，谐振电容和松耦合变压器构成谐振变换器。由于谐振变换器的滤波作用，当逆变电压频率为副边电路自然谐振频率时，谐振电流为近似正弦波。为方便分析，假设电路中电流、电压只有正弦基波分量并忽略松耦合变压器初、次级绕组内阻及开关管导通电阻，建立ICPT互感耦合模型如图2所示。

图2 ICPT互感等效电路Fig.2 Mutual inductance equivalent circuit of the ICPT system

图2 中，Lp、Ls是变压器初、次级绕组自感;M为互感;Cp、Cs为补偿电容;RL是交流等效负载，RL=2πR/8，R是实际负载;Zr是次级绕组等效到初级的反映阻抗可由式(1)表示为

其中，Zs为

因此，初级绕组的总阻抗可由式(3)表示为

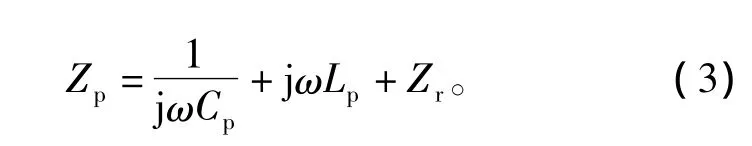
Zr的表达式可由式(2)代入式(1)得到

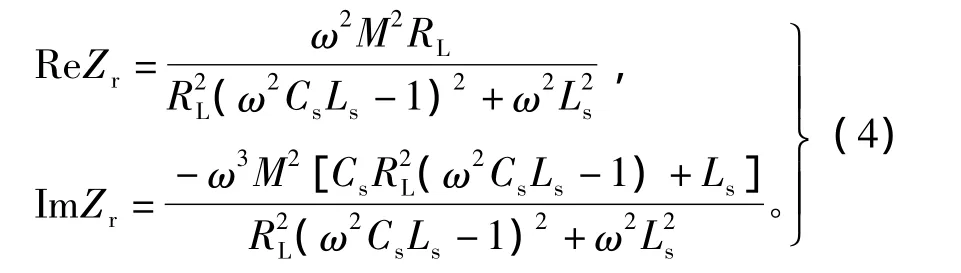
ICPT设计的原则为:松耦合变压器初、次级回路都工作在谐振状态，且具有相同的谐振频率时，系统效率较高。ICPT的谐振频率根据实际应用场合及松耦合变压器的大小、类型确定，谐振频率的设计这里不作讨论。假设系统谐振频率为ω0，由设计原则可知次级绕组补偿电容可由式(5)得到

初级绕组同样也工作在频率ω0的谐振状态，即初级绕组总阻抗虚部要为零。因此，令式(3)虚部为零，可得初级绕组补偿电容为

设计一台便携式设备无线供电系统，输入电压:Uin=24 V，输出电压:Uout=24 V，负载最大功率:P=10 W，负载额定电阻:RL=10 Ω，互感耦合系数为0.45。补偿结构为SP方式，ICPT主要参数如表1所示。

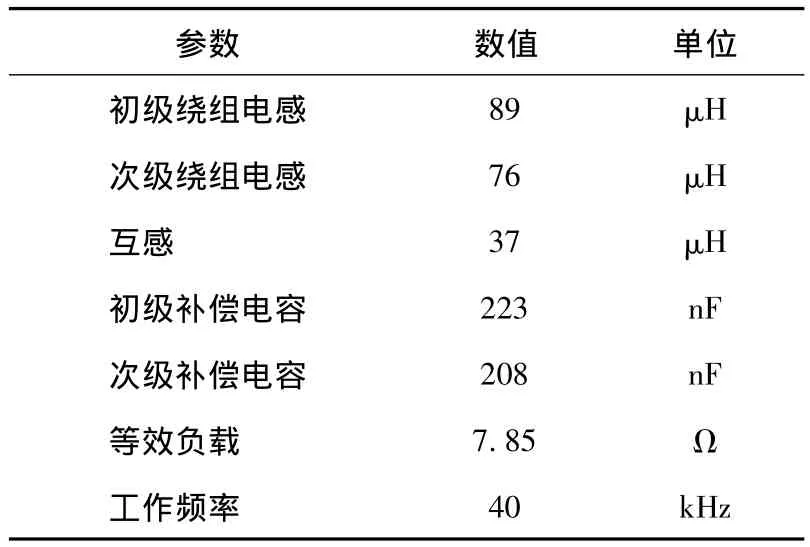
表1 ICPT系统主要参数Table 1 ICPT system main parameter

2 变频控制的频率分叉问题分析

由上述分析可知，选择合适的补偿电容可以使ICPT系统工作在谐振状态，但是，当负载变化时系统会偏离谐振频率点，这样输出电压就会波动。谐振腔电流和电压也会有相位差，系统效率也会降低。为得到稳定的输出电压，可通过调节频率的方式控制输出电压［20］。在频率跟踪模式下，当输出电压与参考电压之差大于零时，增大工作频率，此时负载阻抗随之增大，因而电压降低。反之，则减小频率，提高电压。因此，通过调节频率可得到稳定的输出电压。根据表1数据绘制系统电压增益及阻抗角θ随工作频率变化规律如图3所示，图中f1=40 kHz时为系统的谐振频率。图3(a)为电压增益随频率变化曲线。当RL=10 Ω时，如图3(a)中虚线所示，当工作频率大于谐振频率时，电压增益随着频率的增大而单调减小，因此可以通过调节频率的方式调节输出电压的大小。而当RL=80 Ω时(此时系统发生频率分叉)如图3(a)中实线部分所示，系统的电压增益不是单调变化的，在谐振频率以上调频不能实现电压增益的单调变化，因此不适用于调频控制。图3(b)为总阻抗角随频率变化趋势图，虚线为负载RL=10 Ω时θ的随频率变化的曲线，实线部分为RL=80 Ω(轻载)时θ的变化曲线。

图3 频率分叉现象Fig.3 Bifurcation phenomena

图3 (b)中，当RL=10 Ω时，假设系统当前工作点为A，如果系统受到干扰移动到A1点，由图可知，A1点阻抗角θ大于A点阻抗角，此时系统阻抗增大，输出电压Uout减小，如图3(a)所示，由变频控制规则，此时应减小工作频率，由图可知频率减小，系统回到工作点A。如果工作点A受到干扰运动到A2点，此时θ减小，Uout增大，根据变频控制规则，增大频率，系统由A2回到A。因此，在变频控制下系统稳定运行。

当RL=80 Ω时，假设当前工作点为B点。如果系统受到干扰移动到B1点，由图可知，B1点阻抗角θ大于B点，此时Uout减小，如图3(a)所示。由变频控制规则，此时应减小工作频率，由图可知频率减小，系统朝远离工作点B的方向运动。因此，B点在变频控制下是不稳定的。

RL=10 Ω时的曲线是单调递增函数，而RL=80 Ω时的曲线是非单调曲线。RL=10 Ω时存在3个使θ=0的谐振频率点，即f0、f1和f2。当工作频率处于f0和f2之间时，θ存在单调递增和单调递减两种情况，这时如果采用上述的变频控制策略系统就不能稳定工作。

3 ICPT系统的自持振荡控制

3.1 ICPT系统自持振荡控制稳定性分析

SSOC的理论基础是描述函数法。描述函数是指系统在满足特定条件下，非线性环节的输出可用基波分量来近似，由此可导出非线性环节的近似频率特性，这样就可以用线性系统理论来分析非线性系统［20－21］。根据描述函数理论，将图1所示 ICPT系统的逆变器视为非线性环节，而谐振回路可看作线性环节，谐振变换器初级绕组电流反馈至非线性环节的输入端，可得到图4所示的ICPT系统的描述函数法表示。

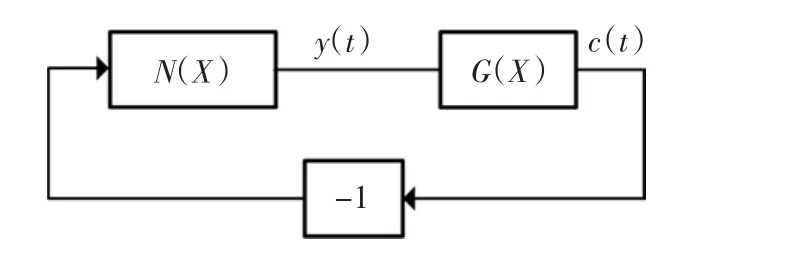
图4 SSOC系统Fig.4 SSOC system

在图4中，逆变器环节N(X)可表示为

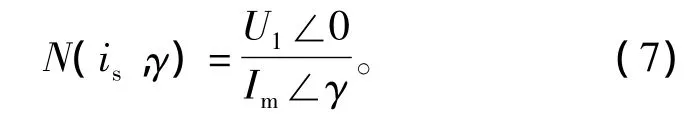
其中:Im为初级绕组电流有效值;γ是初级绕组电流滞后逆变器输出基波电压的相位角。U1为逆变器输出基波电压的有效值，由傅里叶变换可得到U1和直流输入电压Ud的关系为

把式(8)代入式(7)可得到N(·)关于初级绕组电流振幅Im和相位角λ的复数表达式为

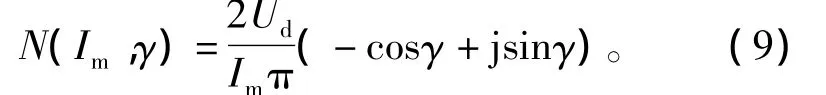
而线性环节即谐振电路传递函数表示为

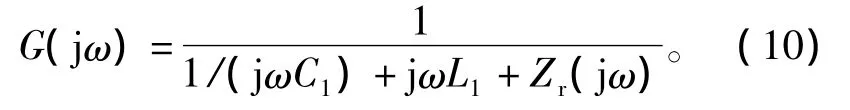
其中Zr(jω)可由式(4)得到。由自持振荡理论［21］可知，若式(11)有解，则其解为系统极限环。

如果极限环是稳定的，则系统工作在自持振荡状态。根据表1参数，绘制式(11)在复平面上，如图5所示。图中实线部分为SSOC系统极限环。

图5 Nyquist曲线Fig.5 Nyquist plot representation

由自持振荡稳定性理论［21］可知，图5中极限环所包围的区域为不稳定区域，极限环以外的区域为稳定区域，G(jω)与 －1/N(Im，γ)的交点为极限环上的点，极限环的稳定性可由李雅普诺夫稳定性理论分析。

图6为在同一复平面内绘制的RL=10 Ω和RL=80 Ω 时的 G(jω)和 N(Im，γ)的图，实线部分为RL=80 Ω，虚线部分为 RL=10 Ω。由图可知虚线部分与γ=0只有一个交点，而实线部分与γ=0有3个交点，说明RL=80 Ω时有3个谐振频率点，表示发生了频率分叉现象，这与第二部分分析结果相同。

图6 Nyquist曲线Fig.6 Nyquist plot representation

ICPT系统在自持振荡控制系统下的稳定性分析如下:当RL=10 Ω的情况，假设系统在A点时受到干扰，则N(X)振幅增大，工作点沿直线方向移动(直线方向为N(X)振幅增大的方向)。最终，工作点会离开G(jω)包围的区域，即系统离开不稳定区域而进入稳定区域，系统稳定则N(X)振幅减小，工作点重新回到A点，所以A点是稳定工作点。从图3中容易得到以下结论，虚线部分的极限环为稳定的极限环，而实线部分内环为不稳定极限环，外环为稳定极限环，即当前工作点在内环时系统不稳定即发生频率分叉，这与论文第二部分结论相同。

以下分析在自持振荡控制下，系统发生频率分叉现象时的稳定性。当RL=80 Ω时，假设系统当前工作点为B点，工作点B正好对应图3中B点，如第二部分所述，变频控制时B点是不稳定点。在图6中，如果B点受到扰动，N(X)振幅增大，工作点沿着直线方向移动直到C点，由上述分析可知C点处于极限环外环是稳定工作点，系统可以通过自持振荡的方式稳定在C。因此，虽然RL=80 Ω时发生了频率分叉现象，但在SSOC控制模式下，系统能工作在稳定状态。

3.2 自持振荡控制器的实现

如图7所示，SSOC控制器由PI调节器、电压比较器、锯齿波发生器和RS触发器4个功能模块组成。PI调节器是调节输出电压Uo跟随参考电压Uref的;误差信号e通过PI调节器，输出信号为γ，γ表征谐振电流滞后逆变器电压的相位角。锯齿波发生器模块不断检测谐振电流过零点并产生两倍谐振电流频率的锯齿波;锯齿波信号和PI调节器的输出信号γ通过电压比较器产生开关导通信号，再通过RS触发器产生互补的两路脉冲信号再驱动开关管。

图7 自持振荡控制系统Fig.7 SSOC system

由图7可知，SSOC控制器上管开关驱动信号总是保持电流滞后电压γ角，因此SSOC控制器在调节电压输出的同时可以实现逆变器的ZVS。另外，与传统VF控制不同的是，SSOC的频率是系统自由振荡得到而不是外界给定。

目前没有现成的芯片可以实现SSOC控制器的功能，可由运算放大器，电阻电容等分立元件构成SSOC控制器，如图8所示。

图8 自持振荡控制器Fig.8 SSOC controller

电流互感器T1检测谐振电流;电压比较器M1不断检测电流过零点并输出与电流同频率的方波，R1，C1组成微分电路对方波信号作微分运算，每半个周期输出一次脉冲信号，波形图如图9(a)所示。运算放大器M4、M5、M6和三极管Q1组成锯齿波发生电路;脉冲电路通过M2、M3、D1、D2组成的绝对值电路后驱动三极管Q1，每半个周期使锯齿波发生电路复位一次，产生如图9(b)所示的两倍于谐振电流的锯齿波。运算放大器M7、电容C2和电阻R2组成的PI控制器的输出与锯齿波信号U3通过电压比较再驱动半桥MOSFET。

图9 自持振荡控制器主要波形Fig.9 Main waveforms of SSOC controller

4 实验验证

按照图1拓扑搭建ICPT实验样机，实验参数采用表1数据。图10是电路稳定工作状态时的相关波形。图10(a)为半桥逆变电压和谐振电流的波形图，图10(b)是开关管Q2漏源极电压UDS和门极驱动电压UGS的波形。

图10 ZVS波形Fig.10 ZVS waveforms

由图10(a)可知，电流相位角γ滞后电压波形，电路工作在感性负载状态，为MOSFET的零电压开通提供了有利条件。由图10(b)可知，当Q2开通后，UDS降为零后，Q2的门极驱动电压UGS才升高，即实现了零电压开关。

图11是VF和SSOC控制下的动态特性图，图11(a)为控制器参考电压为24 V时的阶跃响应，图11(b)为当负载由10 Ω变为80 Ω时，输出电压的动态响应波形图。

图11 动态性能Fig.11 Dynamic performance

由图11可知，SSOC控制器的动态性能优于VF控制。当负载变轻时，此时系统的频率分叉现象发生，VF控制器不能稳定工作，而SSOC控制下，输出电压能够趋于稳定，与论文第4部分分析相符合。

5 结论

将非线性理论的自持振荡控制应用到感应电能传输系统中。当系统负载变轻而发生频率分叉时，系统能在自持振荡控制器的作用下自由振荡而趋于稳定。首先，基于描述函数建立了ICPT系统自持振荡系统，并分析了频率分叉时，系统在自持振荡下是稳定的。最后，实验验证了基于SSOC的ICPT系统具有较好的稳定性和动态性能，并且能始终保持ZVS软开关。

［1］赵争鸣，张艺明，陈凯楠.磁耦合谐振式无线电能传输技术新进展［J］.中国电机工程学报，2013，33(3):1－13.ZHAO Zhengming，ZHANG Yiming，CHEN Kainan.New progress of magnetically-coupled resonant wireless transfer technology［J］.Proceedings of the CSEE，2013，33(3):1－13.

［2］翟渊，孙跃，戴欣，等.磁共振模式无线电能传输系统建模与分析［J］.中国电机工程学报，2012，32(12):155－160.ZHAI Yuan，SUN Yue，DAI Xin，et al.Modeling and analysis of magnetic resonance wireless power trasmission systems［J］.Proceedings of the CSEE，2012，32(12):155－160.

［3］HU A P.Selected resonant converters for IPT power supplies［D］.Auckland:The University of Auckland，2000.

［4］武瑛，严陆光，徐善纲.新型无接触电能传输系统的稳态性能分析［J］.中国电机工程学报，2004，24(5):63－66.WU Ying，YAN Luguang，XU Shangang.Stability analysis of the new contactless power delivery system［J］.Proceedings of the CSEE，2004，24(5):63－66.

［5］曹玲玲，陈乾宏，任小永，等.电动汽车高效率无线充电技术的研究进展［J］.电工技术学报，2012，27(8):1－13.CAO Lingling，CHEN Qianhong，REN Xiaoyong，et al.Review of the efficient wireless power transmission technique for electric vehicles［J］.Transactions of China Electrotechnical Society，2012，27(8):1－13.

［6］白亮宇，唐厚君，徐阳.经表皮能量传输系统电气参数优化设计［J］.电机与控制学报，2011，15(9):12－17.BAI Liangyu，TANG Houjun，XU Yang.Parameter optimization of the transcutaneous energy transmission system［J］.Transactions of China Electrotechnical Society，2011，15(9):12－17.

［7］HIRAI J，KIM TW，KAWAMURA A.Study on intelligent battery charging using inductive transmission of power and information［J］.IEEE Transactions on Power Electronics，2000，2(15):335－345.

［8］王璐，陈敏，徐德鸿.磁悬浮列车非接触紧急供电系统的工程化设计［J］.中国电机工程学报，2007，27(18):67－70.WANG Lu，CHEN Min，XU Dehon.The engineering design of contactless emergency power supply in maglev［J］.Proceedings of the CSEE，2007，27(18):67－70.

［9］LIU X，HUI S Y.Optimal design of a hybrid winding structure for planar Contactless battery charging platform［J］.IEEE Transactions On Power Electronics，2008，23(1):455－463.

［10］马皓，孙轩.原副边串联补偿的电压型耦合电能传输系统设计［J］.中国电机工程学报，2010，30(15):48－52.MA Hao，SUN Xuan.Design of voltage source inductively coupled power system with series compensation on both sides of transformer［J］.Proceedings of the CSEE，2010，30(15):48 －52.

［11］周雯琪，马皓，何湘宁.基于动态方程的电流源感应耦合电能传输电路的频率分析［J］.中国电机工程学报，2008，28(3):119－124.ZHOU Wenqi，MA Hao，HE Xiangning.Frequency analysis of a current source inductively coupled power transfer system based on dynamic circuit equations［J］.Proceeding of the CSEE，2008，28(3):119－124.

［12］杨民生，王耀南，欧阳红林，等.基于可控电抗器的无接触电能传输系统动态补偿［J］.电工技术学报，2009，24(5):183－189.YANG Minsheng，WANG Yaonan，OUYANG Honglin.Dynamic compensation of contact-less power transmission system based on controlled reactor［J］.Transactions of China Electrotechnical Society，2009，24(5):183 －189.

［13］孙跃，杨芳勋.基于移相直通控制策略的IPT系统输出功率调节［J］.电工技术学报，2012，27(10):6－12.SUN Yue，YANG Fangxun.Regulation of inductive power transfer system based on phase shifting-short control strategy［J］.Transactions of China Electrotechnical Society，2012，27(10):6－12.

［14］戴欣，余奎，孙跃.CLC谐振感应电能传输系统的∞控制［J］.中国电机工程学报，2010，30(30):47－54.DAI Xin，YU Kui，SUN Yue.Study on∞ control method for CLC resonant inductive power transfer system［J］.Proceedings of the CSEE，2010，30(30):47－54.

［15］韩腾，卓放，闫军凯，等.非接触电能传输系统频率分叉现象研究［J］.电工电能新技术，2005，24(2):44－76.HAN Teng，ZHUO Fang，YAN Junkai，et al.Study of frequency bifurcation phenomenon of a Contactless power transmission system［J］.Advanced Technology of Electrical Engineering and Energy，2005，20(11):56－59.

［16］CHWEI Sen Wang，GRANT A，COVIC.Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems［J］.IEEE Transactions on Industrial electronics，2004，1(51):148－157.

［17］孙跃，王智慧，戴欣.非接触电能传输系统的频率稳定性研究［J］.电工技术学报，2005，20(11):56－59.SUN Yue，WANG Zhihui，DAI Xin，et al.Study of frequency stability of contactless power transmission［J］.Transactions of China Electro Technical Society，2005，20(11):56 －59.

［18］戴欣，周继昆，孙跃.具有频率不确定性的π型谐振感应电能传输系统∞控制方法［J］.中国电机工程学报，2011，31(30):45－53.DAI Xin，ZHOU JiKun，SUN Yue.∞ control method with frequency uncertainly for π type resonant inductive power transfer system［J］.Proceedings of the CSEE，2011，31(30):45－53.

［19］LE POURHIET AL，CORREGE M，CARCUANA D.Control of self-oscillating systems［J］.IEEE Proceedings Control Theory and Applications，2003，150(6):599－610.

［20］JORGE Luis Sosa，MIGUEL Castilla，JAUME Miret.Modeling and performance analysis of the DC/DC series-parallel resonant converter operating with discrete self sustained phase shift modulation technique［J］.IEEE Transactions on Industrial Electronics，2009，56(3):697 －705.

［21］吴俊娟，孙孝峰，邬伟扬.基于描述函数法的谐振变换器自持振荡研究［J］.电力电子技术，2011，45(2):53－55.WU Junjua，SUN Xiaofeng，WU Weiyang.Study of the self-sustained oscillation of resonant converter based on describing function method［J］.Power Electronics，2011，45(2):53 －55.