大功率直线感应电动机推力脉动研究

聂世雄， 孙兆龙， 马伟明， 马名中， 许金， 鲁军勇， 张育兴

(海军工程大学舰船综合电力技术国防科技重点实验室，湖北武汉430033)

0 引言

直线感应电动机(linear induction motor，LIM)在汽车加速碰撞试验、电磁发射等大载荷运输场合的应用受到越来越高的关注［1－3］，且随着负载质量及出口速度的增加，直线电机的功率日益增大。为了满足高速度要求，直线电机设计为双边长初级短次级结构且次级不含铁心仅为一块铝板，磁路在双边初级铁心形成闭合回路。边端效应是直线电机初级铁心和次级开断所致的固有效应［4－5］，该效应会引起电机电磁推力不同频率的脉动。静态纵向边端效应是由直线电机初级铁心的开断所致，表现出来为电机各相互感不对称，即通入各相对称电压，各相电流不平衡［6－8］，其中负序电流会引起推力工作频率两倍频的脉动。动态纵向边端效应是由次级的开断所致，即在次级运动过程中，次级进入端的表面磁场是从空载气隙值减小到气隙合成值，次级滑出端是从气隙合成值增大到空载气隙值［9］。表现出来的即为次级边端感应涡流局部增加，且产生一个转差频率两倍频的推力脉动。推力脉动的存在增加了电机高平稳控制的困难，因此很多文献对如何在控制过程中消除边端效应的影响进行了较为详细的研究，其方法主要是对等效电路和参数进行修正［10－17］。虽然这些边端效应补偿方法在仿真和试验验证中起到了一定的效果，但没有文献对上述双边长初级短次级直线感应电动机的静态和动态纵向边端效应对电磁推力的影响机理、推力脉动频率和推力脉动幅值进行过系统、详细的研究。

本文首先根据直线感应电动机电磁推力表达式推导得到了静态和动态纵向边端效应所引起推力脉动频率。然后建立直线电机电磁分析模型，基于电磁场方程对动态纵向边端效应的影响机理进行了解析计算，得到了计及动态纵向边端效应时次级感应涡流的分布规律，据此计算得到了动态纵向边端效应所引起的推力脉动幅值及其和电机参数的关系。上述分析计算结论的正确性通过峰值功率20MW，最大出力900kN的大功率直线感应电动机实验系统静态推力测试进行了验证。

1 推力脉动频率分析

假设直线感应电动机为三相电机，且沿次级运动方向的绕组分布为 A+C－B+A－C+B－。，由于静态纵向边端效应的影响，电机三相互感不相等［8］，在施加对称电压的情况下，直线电机初级三相电流不平衡，经对称分量变换后分别存在正序、负序和零序分量;同理由于动态纵向边端效应的影响，直线电机次级三相电流也不平衡，经对称分量变换后分别存在正序、负序和零序分量。零序电流产生的脉振磁场对电磁推力没有影响，因此在后续的分析中不予考虑，于是可以得到直线电机初级和次级电流分别如式(1)、(2)所示。

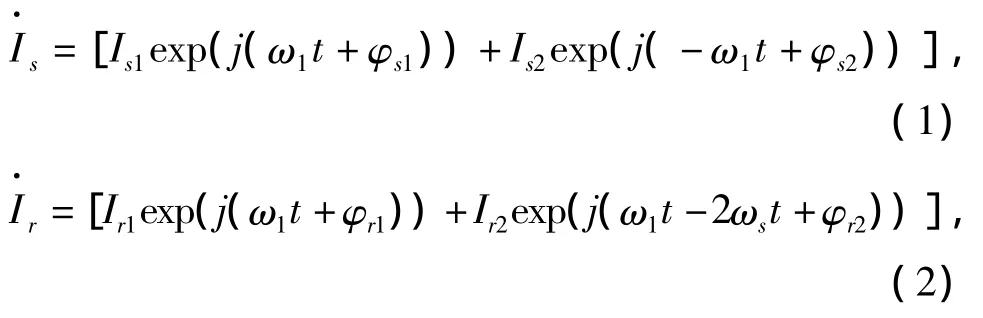
其中:I为电流幅值，ψ为相位角，ω为电角频率，下标s，r分别代表初级量和次级量，下标1，2分别代表正序和负序分量，ωs为转差电角速度。

电磁推力的表达式如式(3)所示。

其中:F为电磁推力，β为线速度角速度转换系数，且有 βg=π/τ，Lm为激磁电感。

分别将初级和次级电流带入到推力表达式可以得到:

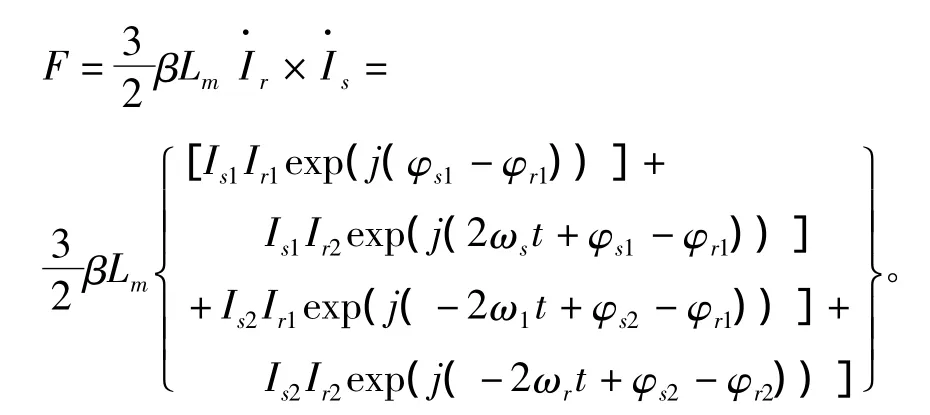
电磁推力公式共包括四项表达式，其中第一项为初级和次级电流正序分量产生的做有用功的电磁推力，在电机参数和电流确定的情况下，该推力为一恒定值;第二项为初级电流的正序分量和次级电流的负序分量产生的推力脉动，脉动频率为转差频率的两倍;第三项为初级电流的负序分量和次级电流的正序分量产生的推力脉动，脉动频率为工作频率的两倍;第四项为初级和次级电流的负序分量产生的推力脉动，由于初级电流的负序分量和次级电流的负序分量和正序分量相比差近一个数量级，因此二者的乘积基本可以忽略不计。

综上，由于直线感应电动机固有的静态纵向边端效应和动态纵向边端效应的影响，电机电磁推力存在两个频率的脉动:静态纵向边端效应引起工作频率两倍频的脉动，动态纵向边端效应引起转差频率两倍频的脉动。其中工作频率两倍频的脉动大小取决于初级电流的负序分量和次级电流的正序分量，转差频率两倍频的脉动大小取决于初级电流的正序分量和次级电流的负序分量。文献［8］对电机静态纵向边端效应的影响机理进行过详细的研究，并得到了其影响规律和电机极数及边端铁心的关系。这里将重点分析由动态纵向边端效应所致的转差频率两倍频推力脉动的影响规律。

2 动态纵向边端效应解析分析

2.1 电机模型及假设条件

电机分析模型包括一个充满整个气隙g的次级铝板，这种结构和铝板只占气隙的一部分是等价的，只是此时次级的等效导电率为σ(w/g)，其中σ为次级铝板材料的体导电率，w为次级板厚度的一半。为便于分析，以次级作为参考坐标系，且沿长度方向定义为变量x，初始位置(x=0)为次级板的最左侧，次级的长度等于电机极距的m倍，即mπ/β，其中β=π/τ。模型示意图如图1所示。

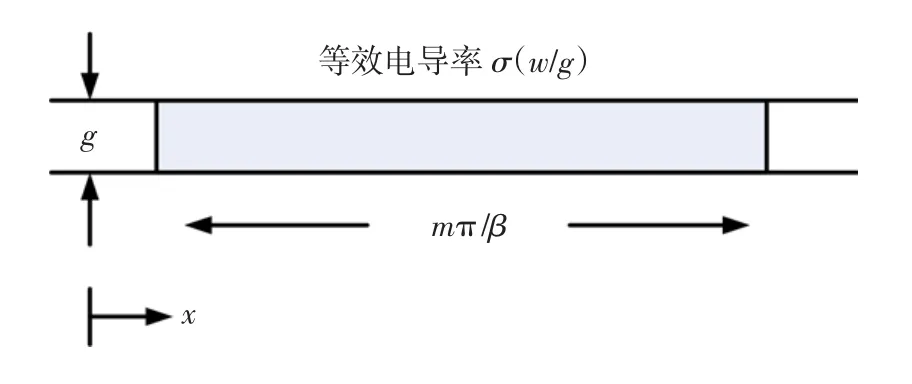
图1 直线电机分析模型Fig.1 Model of LIM

为了便于分析，需要对模型进行简化，因此做如下假设:

1)气隙为常数，即定子表面到次级的中心线距离为常数;

2)定子绕组为正弦分布，即忽略绕组谐波效应;

3)忽略横向边端效应;

4)和极距相比，气隙足够小，即可以利用一维磁路法来求解;

5)假设电机铁心不饱和。

2.2 电磁场方程

2.2.1 电机激励

次级感应涡流的激励源是定子电流产生的磁场。磁场强度定义为Hs，该激励相对于次级以转差角速度ωs在运动，于是激励源可以表达为:

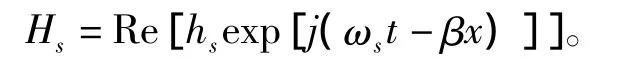
其中:hs为激励源的幅值，为常数，和定子电流层的幅值K有关:

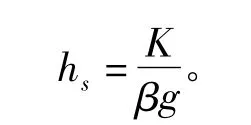
K取决于绕组布置方案，且和线圈的电流密度幅值相关。

2.2.2 电磁场方程

次级铝板感应涡流产生的磁场强度定义为T，则根据麦克斯韦方程组的安培定律，可以得到次级铝板的感应涡流J如下式所示。

气隙磁场的磁场强度等于定子绕组电流产生的磁场强度和次级感应涡流产生的磁场强度之和，如下式所示。

其中:H为气隙磁场强度，Hs为定子绕组电流产生的磁场强度。

可以继续写出Faradays电磁感应定律的积分形式:

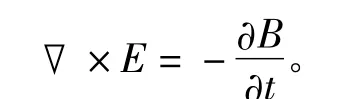
考虑到次级板和气隙的相对磁导率为μ0，我们可以将Faradays电磁感应定律的积分形式依据之前定义的变量得到其稳态形式:

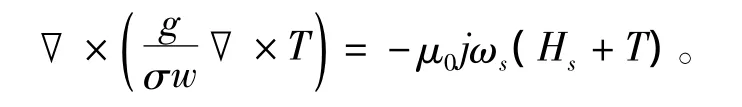
将系数提出，根据T的散度为零可以得到:

为了简化方程描述，调用一个“边端系数”:

根据该系数，可以得到次级板上的感应涡流分布方程:

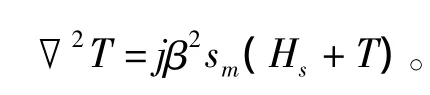
根据该方程可以求解得到考虑边端效应时的次级感应涡流，从该方程同样可以得到推力的修正系数，这是一个关于空间变量x的二阶微分方程。

2.3.3 边界条件:

为了解决上述二阶微分方程，必须在次级板边端设置边界条件，边界条件如下:

1)电流分布在次级板内部;

2)当x趋于无穷时，与次级相关的干扰可以忽略。

这些标准和下列数学式等价:

次级板上的净电流等于次级边端电矢位T的微分，只要次级边端值相同，电流守恒即满足(基尔霍夫电流定律)。设置T=0，则次级电流在次级外的区域没有影响，令无穷远处的磁场为源磁场。

2.3.4 方程求解

对次级内部的T进行求解可以分成两个部分:

1)考虑次级板对场源反应时/将次级板视为无穷大的解法/在次级的边端不满足/T=0的条件/，将该部分定义为T1;

2)因补偿边界条件产生的次级边端局部扰动，定义该部分为T2。

因为T1部分的解法类似于将次级视为无穷长，故具体求解过程不再赘述，结果如下:

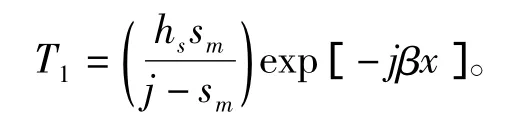
注意到次级边端(x=0，mπ/β)存在如下条件:

现在，T2解法满足如下边界条件的解法的一部分:

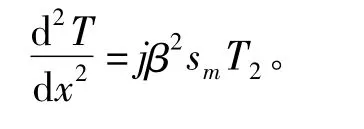
且满足如下边界条件:

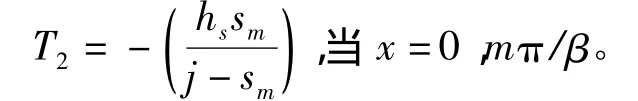
利用常规的微分方程求解方法，可以得到:

这种形式的求解结果并不直观，如果次级极数足够多，边端效应基本没有影响，上述解法和考虑边端效应的指数衰减扰动较为接近:

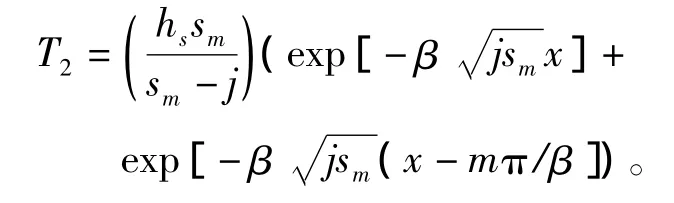
那么，次级板的总电流分布式如下(利用T2的近似表达式):

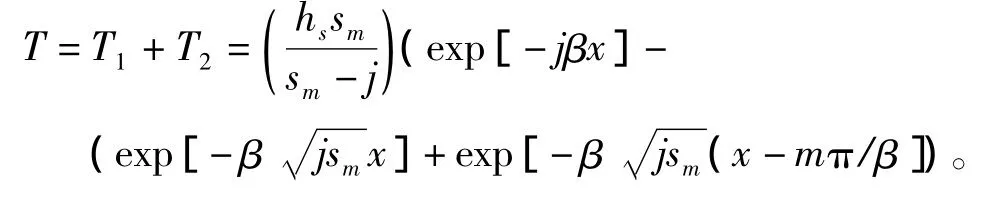
所以次级板的电流密度为:

其中g/w系数为实际的次级宽度和总的气隙比，将上式展开即可得到电流密度的表达式:

根据上述解析表达式不难得到动态纵向边端效应所引起的次级感应涡流脉动及其随参数变化规律:

1)次级边端存在较大电流脉动，会引起次级局部过热;

2)当sm增加时边端效应脉动增加;

3)sm增加时，边端效应脉动在短距离内削弱。

3 电磁推力计算

既然已经得到次级板感应涡流的解答方法，该方法同样适用于推导出相对于无限长次级板模型的电磁推力。电磁推力通过在整个次级板内的区域对JxB积分得到，对于一半厚度的次级板，单位定子长度产生的推力为:

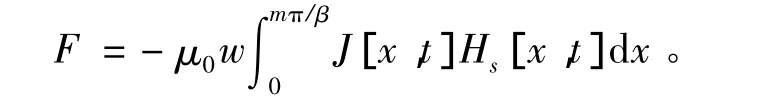
注意到既然次级板边端效应表现出(等效三相电流)不平衡性，因此其推力应该会出现转差频率两倍频的波动(定子侧的三相电流不平衡会出现推力的供电频率两倍频的波动)，为了正确的得到该分量，积分中利用的J和Hs均是时间的函数。

电磁推力的综合表达式非常复杂和繁琐，电磁推力的稳态部分(sm＞0)为

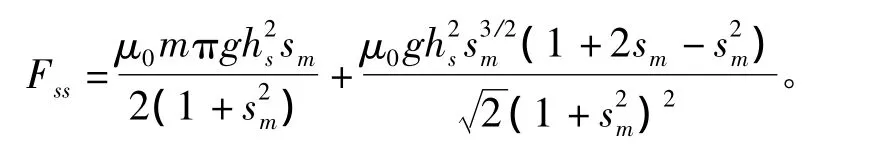
其中上述表达式的第一部分为忽略边端效应时m极次级的推力，第二个部分则为边端效应引起的电磁推力。有趣的是，边端效应所引起的推力在转差频率为 1 +时为正向推力，过了该点后则为反向推力。该电磁推力的震荡频率为转差频率的两倍，其幅值为:

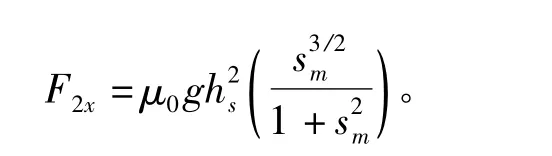
将电机参数带入，利用Matlab绘图可以得到两个推力随转差频率的变化关系分别如图2和图3所示。

图2 不考虑边端效应的电磁推力随转差频率变化曲线Fig.2 Curve of thrust vs.slip frequency

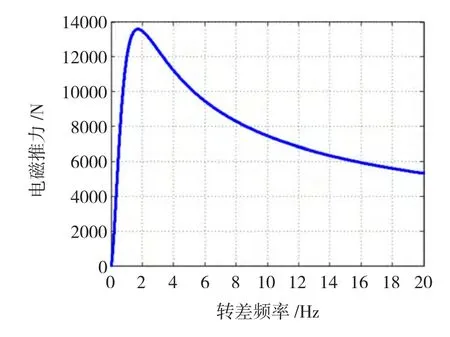
图3 推力脉动峰值随转差频率变化曲线Fig.3 Curve of thrust ripple vs.slip frequency

在电流和转差频率一定的情况下，不考虑边端效应时的推力为一恒定值，而边端效应引起的推力脉动幅值和频率也是固定的，假设不考虑电流上升过程，电流维持3 s内的计算推力波形如图4所示。

图4 固定电流和转差频率时的推力曲线Fig.4 Curve of thrust at fixed slip frequency and current

以15极次级为例，设计转差频率约为1 Hz，对于该情况，脉动系数约为3.6%。由于推导该公式时坐标定位在次级上，且忽略定子和次级的速度差，故该公式适用于低转差频率的工况，即次级速度约为同步速度。

4 试验验证

本文试验数据来自大功率直线感应电动机，最大出力900 kN，峰值功率20 MW。性能测试主要是堵转工况时的电磁推力测试。试验系统以储能电机作为试验电源，经过整流器和逆变器转换成所需的频率和幅值的三相电压给直线感应电动机供电，利用高精度LEM电流霍尔传感器、高压探头以及高采样频率数据采集系统采集电机端口电压、电流波形。电磁推力采用拉力计测量(量程100吨，精度0.1吨)。直线感应电动机及其试验设备如图5所示。

图5 大功率直线感应电动机试验装置Fig.5 Experimental facility of LIM

6 000 A、4 Hz的静态推力测试工况下的实测电流曲线如图6所示，实测推力曲线如图7所示。

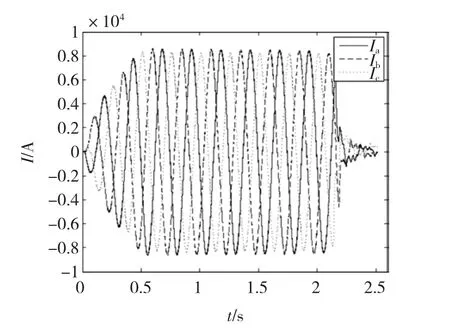
图6 实测三相电流波形Fig.6 Experimental current waveform

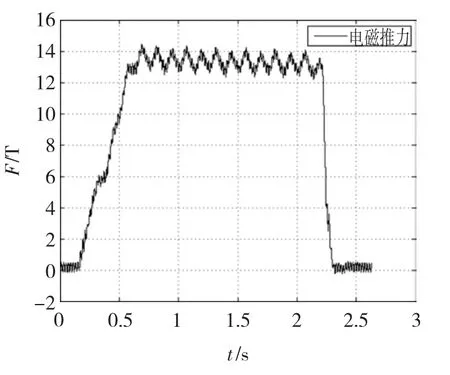
图7 实测推力波形Fig.7 Experimental thrust waveform

由于电流闭环控制克服了静态纵向边端效应，据图6可看出三相电流对称性较好，可忽略静态纵向边端效应引起的工作频率两倍频的脉动。观察图7所示的推力曲线不难看出存在一个转差频率两倍频(8Hz)的脉动，脉动系数约为5.9%，该脉动即为动态纵向边端效应引起，根据脉动系数计算公式可以得到脉动系数为7.2%，和实测值吻合较好。

另外，根据图6和图7可以看出在通电时间内电流和推力在逐渐减小，这主要是因为瞬时大电流导致电机铁心和绕组发热从而引起电机阻抗增加，在电压不变的情况下，电流会逐渐减小。由于转差频率没有变化，因此电流的减小会导致推力逐渐降低。

5 结论

本文对直线电机固有的边端效应引起的推力脉动进行了研究，其中重点利用简化模型推导得到动态纵向边端效应对电机次级铝板感应涡流及推力性能的影响，并得到如下结论:

1)直线电机电磁推力存在两个频率的脉动:静态纵向边端效应引起工作频率两倍频的脉动，动态纵向边端效应引起转差频率两倍频的脉动。

2)动态纵向边端效应导致次级铝板边缘产生较大电流脉动，从而导致次级边端局部过热。

3)动态纵向边端效应导致次级等效三相电流不均衡，故产生的电磁推力存在一个两倍转差频率的脉动，脉动系数约为3.6%;

4)在低转差频率的前提下可以利用分析所得的公式计算由动态纵向边端效应引起的推力脉动。

如何利用上述分析结论并通过控制算法消除边端效应对电机电磁推力的影响，从而达到对负载平稳加速的目的，尚需进一步研究。

［1］DOYLE M R，SAMUEL D J，CONWAY T.Electromagnetic aircraft launch system-EMALS［J］.IEEE Transactions on Magnetics，1995，31(1):528 －533.

［2］DOYLE M，SULISH G，LEBRON L.The benefits of electromagnetically launching aircraft［J］.Naval Engineering Journal，2000，112(3):77－82.

［3］WOLCOT B.Induction for the birds［J］.Mechanical Engineering，2000，122(2):66 －70.

［4］龙瑕令.直线感应电动机的理论和电磁设计方法［M］.北京:科学出版社，2006:38.

［5］叶云岳.直线电机原理与应用［M］.北京:机械工业出版社，2000:41－45.

［6］鲁军勇，马伟明，李朗如.高速长初级直线感应电动机纵向边端效应研究［J］.中国电机工程学报，2008，28(30):73 －78.LU Junyong，MA Weiming，LI Langru.Research on longitudinal end effect of high speed long primary double-sided linear induction motor［J］.Proceedings of the CSEE，2008，28(30):73 －78.

［7］鲁军勇，马伟明，孙兆龙，等.多段初级直线感应电动机静态纵向边端效应研究［J］.中国电机工程学报，2009，29(33):95－101.LU Junyong，MA Weiming，SUN Zhaolong，et al.Research on static longitudinal end effect of linear induction motor with multisegment primary［J］.Proceedings of the CSEE，2009，29(33):95－101.

［8］孙兆龙，马伟明，鲁军勇，等.长初级双边直线感应电动机静态纵向边端效应及阻抗矩阵研究［J］.中国电机工程学报，2010，30(18):72 －77.SUN Zhaolong，MA Weiming，LU Junyong，et al.Research of static longitudinal end effect and impedance matrix for long primary double-sided linear induction motors［J］.Proceedings of the CSEE，2010，30(18):72 －77.

［9］鲁军勇，马伟明，许金.高速长初级直线感应电动机纵向边端效应研究［J］.中国电机工程学报，2008，28(30):73 －78.LU Junyong，MA Weiming，XU Jin.Longitudinal end effect research of high speed long primary linear induction motors［J］.Proceedings of the CSEE，2008，28(30):73 －78.

［10］FUJII N，HOSHI T，TANABE Y.Methods for improving efficiency of linear induction motor for urban transit［J］.Mechanical Systems，Machine Elements and Manufacturing，2004，47(6):512－517.

［11］KIM Daekyong，KWON Byungil.A novel equivalent circuit model of linear inductionmotor based on finite element analysis and its coupling with external circuits［J］.IEEE Trans Magn，2006，42(10):3407－3409.

［12］DOLINAR D，STUMBERGER G，GRCAR B.Calculation of the linear induction motor model parameters using finite element［J］.IEEE Trans Magn，1998，34(5):3640－3643.

［13］AHN Sungchan Jr，LEE Jungho，HYUN Dongseok.Dynamic characteristic analysis of LIM using coupled FEM and control algorithm［J］.IEEE Trans Magn，2000，36(4):1876 －1880.

［14］IM D H，KWON B I，LEE J H.Dynamic characteristics analysis of LIM’s vector control using FEM［J］.Proceedings of LDIA’95，1995:307－310.

［15］IM D H，KIM C E.Finite element force calculation of a linear induction motor taking account of the movement［J］.IEEE Trans on Magnetics，1994:30(5):3495 －3498.

［16］DUNCAN J，ENG C.Linear induction motor-equivalent-circuit model［J］.Proc Inst Electr Eng，1983，130(1):51 －57.

［17］PAI R M，BOLDEA I，NASAR S A.A complete equivalent circuit of a linear inducion motor with sheet secondary［J］.IEEE Trans Magn，1988，24(1):639－654.