提高电磁平衡头运动平稳性的驱动参数优选方法

杨婷婷， 景敏卿， 樊红卫， 刘恒

(西安交通大学机械工程学院，陕西西安710049)

0 引言

对于旋转机械，转子不平衡是最常见故障之一。特别是，高速和超高速磨削中，转子不平衡会使高速旋转的砂轮产生极大的惯性离心力，从而引发支撑系统的强烈振动，导致刀具——主轴单元的使用寿命和工件的表面质量迅速下降。因此，机床主轴需要进行在线自动动平衡以降低同步振动的影响。

自动平衡装置是不停机状态下转子进行在线动平衡的执行机构、也是最核心部件。已有的自动平衡装置主要有机械式［1－2］、注液式［3－4］和仿电机式［5－6］。新型的电磁式自动平衡装置因其具有非接触、响应快、结构紧凑、设计灵活、平衡转速高等特点，已成为自动平衡装置的主要发展方向［7］。

本课题组针对国产170MD12Y16磨削电主轴自主设计了一款电磁－永磁混合驱动的平衡头装置［8－9］。该平衡头由动环和静环两个部分组成，平衡头的作动主要依赖于线圈通电将齿状磁性盘磁化后与永磁体之间产生的磁力来推动配重盘转动。配重盘受到的电磁力矩的变化是影响电磁平衡头作动平稳性的主要因素。电磁驱动力矩的变化主要受磁性齿盘结构和驱动电流两方面的影响，因此如何优化磁性盘的结构及如何优选驱动电压的波形参数是电磁平衡头运动平稳性优化的最主要思路。其中，从结构角度来抑制电机的电磁转矩脉动的研究已经较多［10－12］，为了避免使平衡头结构复杂化，本文主要从驱动角度来讨论如何抑制电磁平衡头的转矩脉动。

1 电磁平衡头结构原理及仿真模型

1.1 配重与平衡原理

本文所研究的电磁平衡头实物［8－9］如图 1所示。

图1 电磁平衡头实物图Fig.1 Prototype machine of electromagnetic balancer

图1 中，平衡头产生配重的核心结构是配重盘，配重盘具体如图2所示，其上开有一定数量配重孔，通过这些配重孔配重盘就能产生一定的平衡质量，两个配重盘的平衡矢量和用于抵消初始不平衡，即平衡原理如图3所示。

图2 配重盘结构示意图Fig.2 Structural diagram of counterweight disc

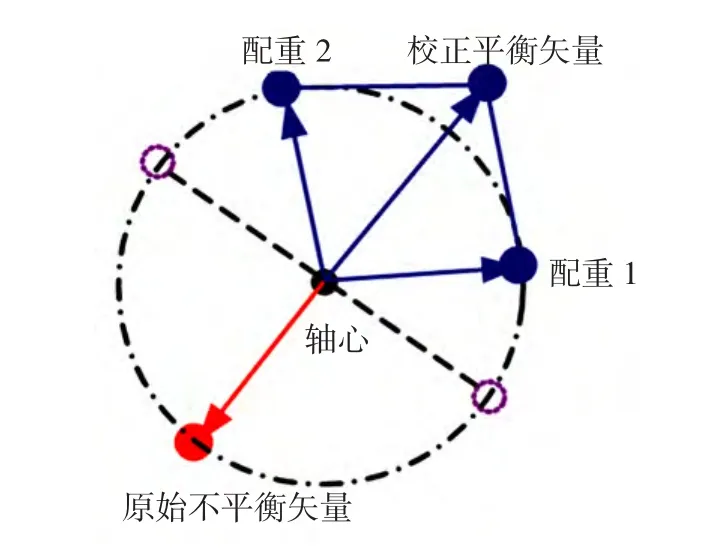
图3 平衡原理示意图Fig.3 Balancing schematic diagram

1.2 作动原理［8－9］

本文研究的平衡头的磁性盘齿数为10，永磁体个数为20且相邻两个永磁体极性相反，配重盘转动一步即转过一个齿厚的距离为配重盘一个“步距”，配重盘转动一圈共20个步距。

为阐述平衡头作动原理，选择配重盘上相邻三个永磁体a、b、c及与配重盘轴向相对的一对齿状磁极凸缘A、B作为研究对象，永磁体a、b、c充磁方向及齿状磁极凸缘A、B相对位置如图4所示。

当配重盘处于不通电的稳定自锁位置(a)时，线圈不通电、齿状磁极凸缘A、B未磁化，此时与凸缘A、B相对的两个充磁方向相反的永磁体a、b与两个凸缘组成的磁路满足磁阻最小原理。当需要配重盘转动时，线圈通电、齿状磁极被磁化，磁极凸缘A、B的磁化方向如(b)所示，通过“同性相斥、异性相吸”原理，凸缘A、B与永磁体a、b产生作用力，凸缘A、B对永磁体a产生斥力FAa和FBa，其合力为Fa;凸缘A、B对永磁体b产生吸力FAb和FBb，其合力为Fb;配重盘在Fa与Fb沿周向的合力F作用下转动。当永磁体b运动到凸缘中心位置时，配重盘沿周向驱动力几乎为0，但由于配重盘已具有一定速度，依靠惯性继续沿原运动方向转动，如(d)所示;将永磁体b从凸缘中心位置转动到下一稳定自锁位置的过程定义为下半程，此时永磁体a逐渐远离凸缘A、B，与凸缘A、B的作用力下降，永磁体c逐渐靠近凸缘A、B，与凸缘A、B的作用力上升，但由于此时线圈通电方向、大小未改变，凸缘A、B对应的磁化方向也未改变，由于永磁体充磁方向恰好相反，永磁体b受到与运动方向相反的吸力，配重盘在驱动力作用下减速运动，如(e)所示;当配重盘运动到下一稳定自锁位置时，线圈断电、外加电磁场消失，永磁体b、c与凸缘A、B组成的磁路满足磁阻最小原理，重新自锁在新的平衡位置，如(f)所示。这就是配重盘转动一个步距的作动过程。当转过一个步距后，同一齿状磁性盘的齿对应的永磁体充磁方向恰好相反，因此要使配重盘沿同一圆周方向连续转动，就要改变电磁场的磁化方向，因此就需要改变电压或电流的方向。

图4 作动原理示意图Fig.4 Actuating schematic diagram

1.3 平衡头三维仿真简化模型

由于磁场分析中存在不可避免的漏磁和饱和问题，这里采用有限元法对平衡头齿槽转矩和驱动力矩进行仿真计算。为减小计算量、缩短计算时间，采用1/20模型(即单盘的1/10模型)。简化的有限元模型及边界条件等如图5所示。

图5 电磁平衡头有限元分析简化模型和边界条件Fig.5 Simplified model and boundary conditions for electromagnetic balancer＇s finite element analysis

2 电磁平衡头驱动优化研究

平衡头的驱动优化主要是选择合理的驱动参数，包括驱动波形、驱动电流大小和电流作用时间。以下基于配重盘运动过程仿真对平衡头在不同驱动参数下的运动平稳性进行理论分析，根据仿真结果选择最佳的驱动参数。

2.1 驱动波形选择

从作动原理可知，要使配重盘连续转动需给线圈施加正、负极性交替的电压，根据欧姆定律，可以确定相应的电流形式。这里，采用“场路耦合”分析方法，在仿真过程中对线圈施加如图6所示的电流形式，主要有三角形、锯齿形和方波三种。

仿真基于ANSOFT Maxwell－3D瞬态磁场求解器进行。首先，定义材料属性，对铁磁材料施加线性磁导率，对永磁体材料施加矫顽力和剩磁。然后，在Maxwell Circuit Editor模块中建立线圈的等效模型，导入主模块后施加于线圈，如图6所示。需要说明的是，图6所示的驱动电流正好可以让配重盘连续转动2步，这里电流施加的时间和断电的时间设计为相同。最后，定义配重盘为运动体。在给定材料和激励后，还需对模型进行网格划分及定义运动机械属性，待检查模型无误后即可进行瞬态求解。在所选的三种驱动电流激励下，平衡头配重盘的运动过程如图7所示。

从图7可以看出:驱动电流为三角波时，配重盘虽然完成了连续2步转动，但是根据曲线形状可知配重盘没有获得稳定自锁状态;驱动电流为锯齿波时，配重盘显然没有实现连续2步运动，在转过1步后出现了振荡现象。因此，这两种波形都不能使平衡头实现预期的运动，如果不能转动到动平衡所需要的位置并可靠地保持住平衡位置，那么平衡头也就丧失了平衡功能。当驱动电流为方波时，配重盘很好地实现了连续2步转动，单步运动平稳且稳定位置能够保持，因此选择方波作为驱动电压的理想波形。

图6 驱动电流波形Fig.6 Drive current waveform

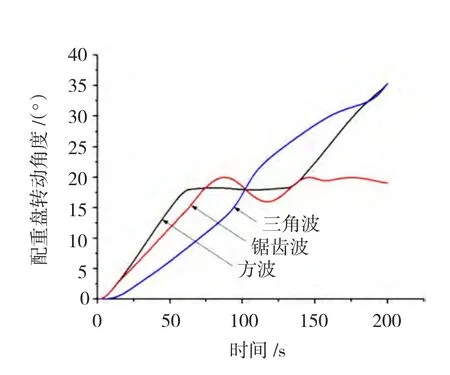
图7 不同驱动波形下配重盘运动角度Fig.7 Movement angles of counterweight disc under different drive waveforms

选定驱动电流波形为方波后，需要选择其中的参数，如电流大小、驱动电流持续时间、断电时间。为了说明参数，方波示意图如图8所示。

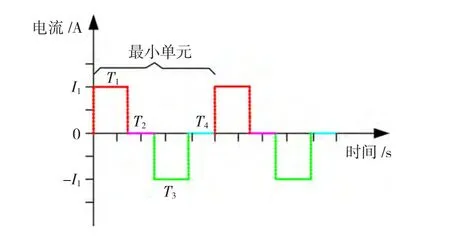
图8 驱动电流示意图Fig.8 Schematic diagram of drive current

图中I1表示方波驱动电流的大小，方波驱动电流的一个周期分为四个时间段:T为通正电流时间，配重盘沿一个方向转动并最终自锁在下一个稳定位置;时间段T2、T4为不通电时间，这段时间线圈充分放电，配重盘不运动;T3为通负电流时间，配重盘沿同一方向继续转动一步并自锁在下一个稳定位置。基于以上描述，可以看出驱动电流的大小和通电的时间都会对平衡头运动状态造成影响。

2.2 驱动电流大小确定

驱动电流大小的仿真采用和波形仿真相同的模型，线圈匝数设计为324匝，通过改变单匝线圈电流的大小来改变线圈的总电流。计算得到在不同驱动电流大小下，配重盘转动一个步距即18°对应的驱动力矩变化趋势，如图9所示。

图9 配重盘驱动力矩－位置关系图Fig.9 Relationship between drive torque and position of counterweight disc

从图9可以看出:当单匝线圈电流较小如2.5 A、2.8 A、3 A时，配重盘在9°前及后的转动过程中，驱动力矩方向都发生了反向，使配重盘作动过程平稳性较差。当线圈电流较大如3.5 A、3.8 A、4 A、4.5 A时，配重盘在9°前及后的转动过程中驱动力矩方向没有发生反向，运动较为平稳。但是，考虑到大的驱动电流带来的大的反向感应电动势和对驱动电路可靠性的严峻考验，这里选择3.5 A作为理想的驱动电流值。

2.3 驱动电流时间确定

驱动电流大小确定之后，再对电流的作用时间进行分析。首先，采用直流输入来确定驱动电流持续时间:当线圈通以持续时间较长的直流电流时，在不考虑机械阻尼力矩情况下，配重盘理论上应该在一个转动步距范围内往复运动，由此往复时间可以确定配重盘转动一个步距所用的时间，进而得到驱动电流的持续时间。仿真所用的电路模型如图10所示，设置直流3.5 A，线圈电阻通过计算或测试均可得到，为2.7 Ω，线圈静态电感为37 mH，在电路上串联电流表，在线圈两端并联电压表。

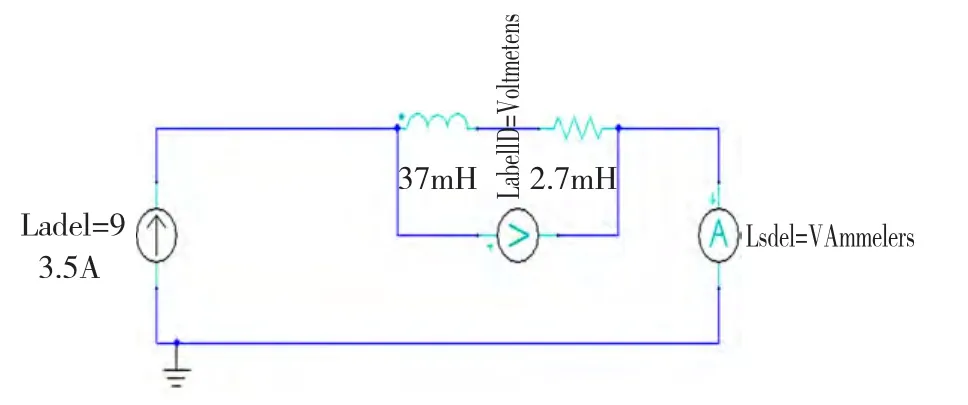
图10 直流驱动输入外电路Fig.10 External circuit of DC drive input

仿真所得配重盘位置随时间变化曲线如图11所示。

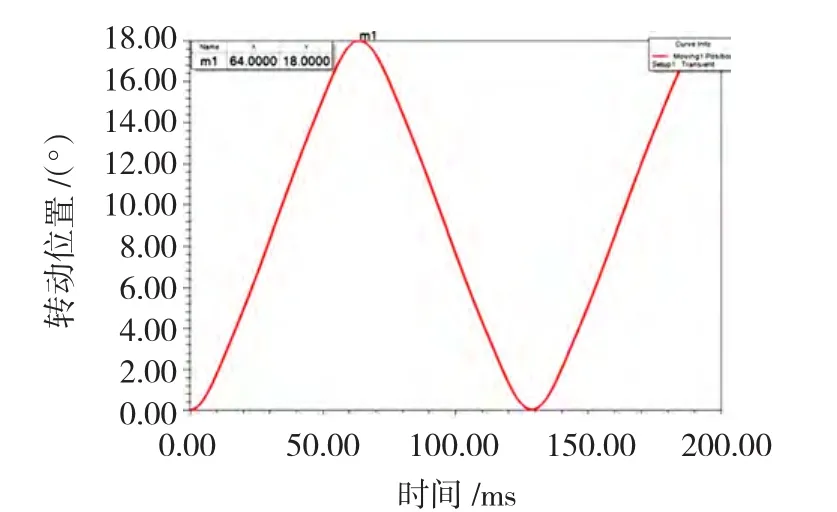
图11 配重盘位置－时间关系图Fig.11 Position vs time relationship of counterweight disc

通过以上仿真，可知配重盘转动一个步距所需的电流持续时间为64 ms。为进一步研究通电时间对平衡头作动过程的影响，分别对驱动电流时间为40 ms(如图12(a))和80 ms(如图12(c))两种情况下配重盘作动过程进行瞬态仿真。配重盘位置变化曲线如图12所示。从图12可以看出，当驱动电流时间较短即40 ms时(断电时间也为40 ms)，配重盘由于线圈放电不充分而出现“跳步”现象，稳定的自锁位置无法获得;当驱动电流时间较长即80 ms时(断电时间也为80 ms)，由于驱动电流时间过长，出现了类似直流驱动的结果即配重盘在转过一个步距后又反向运动使平衡头不能实现朝一个方向连续转动。因此，理想的驱动电流持续时间为64 ms(如图12(b))，此时配重盘既能实现平稳的单步转动、稳定位置的保持，又能实现朝一个方向的连续多步转动。当然，即使电流参数选取在合理范围内，反向感应电动势带来的积累效应也会在多步转动过程中显现出来，只要该效应不影响平衡头的平稳运行，工程上均是可以接受的。

3 实验验证

在实验室建立了如图13所示的实验测试系统，包括平衡头驱动控制模块、平衡头本体实验平台、CoCo80振动测试仪和EDM数据处理软件。实验过程是:平衡头驱动控制系统发出指令使平衡头运动，安装在实验台上的电涡流位移传感器测取转轴的位移信号，然后将信号传给CoCo80信号分析仪进行采集与分析，最后通过EDM软件对数据进行特征提取和查看。所用的电涡流位移传感器为广州精信公司JX20L系列，灵敏度为4 V/mm。需要说明的是，驱动电流大小根据以上分析在实验中设定为3.5 A。实验结果如表1。

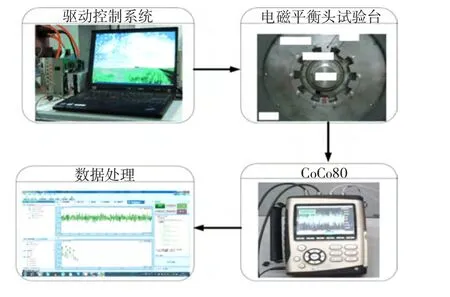
图13 实验系统Fig.13 Experimental system

表1 轴不转时平衡头运动过程Table 1 Operation process of balancer when spindle is stationary

图14进一步依据电涡流传感器的信号分析结果给出了不同驱动参数下的具体位移数值。

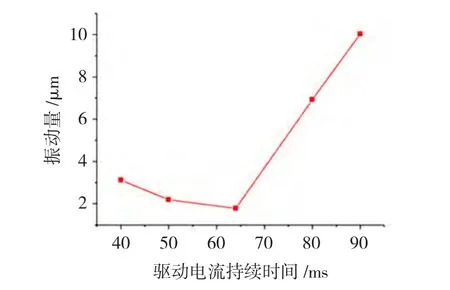
图14 不同驱动电流时间时转轴振动情况Fig.14 Vibration of shaft for different drive times

从表1和图14可以看出:电流持续时间很短或较长时如40 ms、80 ms、90 ms，平衡头不能实现单步或连续转动;电流持续时间选取如50 ms时，配重盘虽能够实现单步和连续转动，但配重盘在转动一个步距后轴的振动比64 ms更大。因此，电流持续时间大约为64 ms时，配重盘能够实现平稳的单步和连续转动，且配重盘转动一个步距后振动很小即对轴的动态特性影响很小。

4 结论

1)阐述了一种新原理电磁平衡头的结构、配重、平衡原理和作动过程，在此基础上引出了平衡头运动平稳性的问题。

2)根据对自主设计的电磁平衡头力分析，提出了三种备选驱动波形，采用电磁场瞬态有限元分析得到了各个波形对应的运动曲线。结果表明，简单的方波驱动可以实现平衡头连续转动。

3)基于方波方案，采用电磁场有限元稳态分析得到了单步转动过程中平衡头力矩－位置关系，据此选定3.5 A(总电流1 134 A)作为线圈单匝激励电流。

4)基于方波和3.5 A电流方案，进一步研究了驱动电流持续时间对平衡头运动过程的影响。在电流占空比为1:1前提下，首先采用直流仿真确定了平衡头电流持续时间的合理取值，然后对多个持续时间进行对比研究。仿真和振动实验均表明电流持续时间取64 ms时可使平衡头获得平稳的运动，此时平衡头转动对轴振动的影响极小。这就保证了平衡头的安装不会对轴带来负面影响，从而为平衡头完成平衡动作提供了技术保障。

5)本文的创新性在于针对一种新原理的电磁平衡头从其驱动能量匹配的角度提出了运动过程的优化方法。通过一个实例研究，证实了该方法的可行性和有效性，为该类电磁平衡头的设计与开发提供了必要支撑;同时，也为电机齿槽转矩的抑制提供参考。

［1］顾超华，曾胜，罗迪威，等.一种机械式在线平衡头的设计与实验研究［J］.振动与冲击，2014，33(12):151－155.GU Chaohua，ZENG Seng，LUO Diwei，et al.Design and experimental study of an on-line balance head mechanical［J］.Vibration and Shock，2014，33(12):151 －155.

［2］张加庆.纯机械式在线动平衡系统的研究［D］.浙江:浙江大学，2006:18－28.

［3］贺世正.释放液体式自动平衡头的研究［J］.浙江大学学报:工学版，2001，35(4):70－74.HE Shizheng.Study of liquid release auto-balancing head［J］.Journal of Zhejiang University:Engineering Science，2001，35(4):70－74.

［4］章云，梅雪松，胡振邦，等.注液式高速切削主轴动平衡装置设计及其性能研究［J］.西安交通大学学报，2013，47(3):13－17，23.ZHANG Yun，MEI Xuesong，HU Zhenbang，et al.Design and performance analysis of hydrojet-typed balancing device for highspeed machine tool spindle［J］.Journal of Xi＇an Jiaotong University，2013，47(3):13－17，23.

［5］陶利民.转子高精度动平衡测试与自动平衡技术研究［D］.湖南:国防科学技术大学，2006:122－123.

［6］杨庆坤.高速主轴在线动平衡装置的设计与研究［D］.北京:北京工业大学，2006:21－26.

［7］樊红卫，景敏卿，刘恒.主动混合式砂轮——电主轴系统自动平衡装置研究综述［J］.振动与冲击，2012，31(5):26－30，41.FAN Hongwei，JING Minqing，LIU Heng.Review of studying on active hybrid auto-balancer of grinding wheel and motor spindle［J］.Journal of Vibration and Shock，2012，31(5):26 －50，41.

［8］樊红卫，景敏卿，王仁超，等.磁力配重型在线自动平衡头的作动原理研究［J］.西安交通大学学报，2013，47(2):97－102.FAN Hongwei，JING Minqing，WANG Renchao，et al.Actuating principle of online automatic balancer with counter weight driven by magnetic force［J］.Journal of Xi＇an Jiaotong University，2013，47(2):97－102.

［9］王仁超.砂轮——电主轴用电磁平衡头本体设计、仿真与实验研究［D］.陕西:西安交通大学，2013:15－35.

［10］张晓宇，王晓远.减少齿槽转矩的无刷直流电机优化设计［J］.微电机，2013，46(1):24 －27，40.ZHANG Xiaoyu，WANG Xiaoyuan.Optimization of design to reduce cogging torque in permanent magnet brushless DC motor［J］.Micromotors，2013，46(1):24 －27，40.

［11］柴凤，李小鹏，程树康.永磁电动机齿槽转矩的抑制方法［J］.微电机，2001，34(6):52－54.CAI Feng，LI Xiaopeng，CHENG Shukang.Methods of restrain cogging torque of permanent magnet motor［J］.Micromotors，2001，34(6):52－54.

［12］黄克峰，李槐树，周羽.利用辅助槽削弱齿槽力的方法研究［J］.电机与控制学报，2014，18(3):54－59，66.HUANG Kefeng，LI Huaishu，ZHOU Yu.Method research for reducing the cogging force by auxiliary slots［J］.Electric machines and Control，2014，18(3):54－59，66.