大型航天器再入陨落时太阳翼气动力/热模拟分析

梁 杰，李志辉，杜波强，方 明

(中国空气动力研究与发展中心超高速所，绵阳621000)

0 引言

大型航天器如空间站或卫星在寿命即将结束时，地面控制中心利用剩余的推进剂进行多次刹车离轨控制，将其轨道高度逐渐减低，然后在无控状态下再入大气层。当再入到120～100 km左右高度时，在大气的作用下开始气动加热。100 km高度左右，太阳翼电池帆板、大型天线等设备在气动热和气动力的双重作用下开始撕裂，并与航天器本体分离。随着航天器表面温度持续升高，航天器局部材料出现软化、结构失效，舱体内外部设备陆续与航天器发生分离。解体后的部件在坠落过程中熔化或燃烧，质量逐渐减小，一些较大的部件则会残留一部分，直到撞击地面。所有的碎片沿航天器的轨迹方向散布在一个狭长的区域［1］。如果解体后的碎片散落在人口密集区，则会对人类的安全造成破坏［2］。这类危险目标的陨落跟踪与落点预报均会引起世界各国的重视，如过去的美国天空实验室、原苏联宇宙1402号核动力卫星、我国失控卫星以及俄罗斯“和平”号空间站的陨落，均受到世界各国的重视，提前进行了再入风险评估［3］。国外开展空间碎片再入预测及地面风险评估的研究已有十多年的历史，并利用工程预测方法形成了相对成熟的软件系统，如美国的碎片评估软件(Debris Assessment Software，DAS)［4］和目标再入存活分析工具(Object Reentry Survival Analysis Tool，ORSAT)［5］，欧洲的航天器大气再入与气动加热解体(Spacecraft Atmosphere Reentry and Aerothermal Breakup，SCARAB)［6］等。国内的清华大学利用工程预测手段初步建立了空间碎片再入分析方法和评估软件［7］。我国的天宫一号目标飞行器由实验舱和资源舱组成，长约7．8 m的太阳翼电池帆板位于资源舱的两侧，两个舱体的总长约10．5 m，舱体最大直径约3．4 m，设计在轨寿命2年。自2011年发射升空后，已经超期服役即将坠入大气层损毁，需要预先对其陨落的风险进行详细的评估，同时还要不断完善这种大型航天器的再入解体和地面风险评估手段，为后续的货运飞船、空间站、大型卫星的陨落风险预报做准备。

关于太阳翼在轨运行的热分析，已有一些文献开展过相关研究［8－9］，但对于大型航天器离轨陨落解体过程中太阳翼帆板的力热分析国内尚属空白。而在航天器再入陨落的初期，流动处于稀薄过渡流区域，求解N－S方程的连续流计算方法已经失效，需要采用基于分子碰撞理论的直接模拟蒙特卡洛(Direct Simulation Monte Carlo，DSMC)方法［10］。文献［11］采用DSMC方法对钝体返回舱外形在稀薄流域的高温真实气体效应进行了计算分析，文献［12］则采用并行DSMC技术开展了过渡流区复杂喷流干扰流动的模拟，尚未针对带太阳翼帆板的大型航天器存在复杂激波干扰环境下的气动特性开展相关研究，因此本文在构建模拟大型复杂航天器高温气体热化学非平衡特性的DSMC数值方法的基础上，对寿命末期离轨陨落的低轨航天器再入稀薄流域120～90 km高度的气动力、热特性进行了模拟分析，重点分析了作用在水平和垂直放置的单侧太阳翼帆板上的力、力矩和峰值压力、热流，为下一步的飞行器结构解体分析提供数据支撑。

1 DSMC数值模拟方法

DSMC方法是通过模拟仿真分子的运动、与边界的碰撞以及分子之间的碰撞随时间的变化，并存贮仿真分子的位置坐标、速度分量以及内能，最后通过统计网格内仿真分子的运动状态实现对真实气体流动问题的模拟。每个仿真分子代表1012～1014个真实气体的分子，该方法的关键是在时间步长Δt内将分子的运动与碰撞解耦。在Δt时间内让所有分子运动一定的距离并考虑在边界的反射，然后计算此Δt内具有代表性的分子间的碰撞。

1．1计算网格及网格自适应

在DSMC方法中，流场中的网格是用来选取可能的碰撞分子对以及对宏观流动参数取样。“天宫一号”目标飞行器结构复杂，涉及到局部凸起物、薄壁和细支架等需要精细描述的复杂壁面，同时计算区域需要覆盖飞行器本体、展开的太阳翼帆板以及激波干扰引起的复杂流动区域，因此网格的计算效率和高可靠性至关重要。在早期的研究中作者采用两级直角网格结构对美国“猎户座”飞船在稀薄流域的气动力系数进行了计算，并与国际知名软件DS3V和DAC的计算结果一致［13］。针对“天宫一号”复杂外形，本文采用计算效率高的流场直角网格和对飞行器几何外形描述精确的表面三角形非结构网格(如图1)，建立了混合网格结构的DSMC数值模拟方法。在描述物面几何形状的非结构网格建立以后，直接将其嵌入到直角网格的流场中，使DSMC计算对流场网格的依赖程度大大降低。同时通过判断分子运动轨迹方程和物面三角形面元上任一点的位置方程，唯一确定出分子与物面的碰撞点坐标，解决了这种混合网格流场分子运动与物面碰撞的难题。对分子在物体三角形面元上碰撞、反射前后的流场参数进行统计取样就可以获得飞行器的整体气动力特性以及表面力、热载荷分布。

图1 计算网格及网格自适应Fig．1 Computational grid and self-adaption

为了解决流场中因激波压缩、激波干扰以及气体膨胀后出现的密度梯度急剧变化的流动特征，计算中采用了网格自适应的策略［14］。即在背景网格的基础上，根据流场中密度梯度的变化分别对碰撞网格和取样网格进行细化(如图1)。由于流场的梯度沿各个方向的变化是不同的，梯度变化大的方向网格细分的更密一些，因此沿三个坐标方向是各自独立地进行自适应，碰撞分子则是在自适应后最小的亚网格内选取，保证了计算的空间精度。

1．2分子转动和振动松弛模型

天宫飞行器再入陨落的速度达到7．6 km/s，需要考虑气体分子的转动和振动激发以及化学反应。连续流气体分子的转动松弛碰撞数和振动松弛碰撞数需要经过内自由度的修正才可用于DSMC的模拟［15］，修正如下:

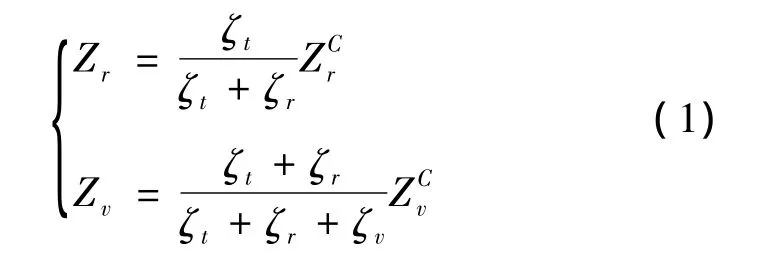
式中:ζt、ζr和ζv分别是分子平动、转动和振动自由度。Parker［16］给出了连续流转动松弛碰撞数ZCr的表达式

式中:T*是气体分子作用势的特征温度，(Zr)∞是实验测定的极限值。

连续流的振动松弛碰撞数定义为

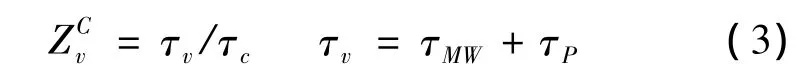
式中:τc为分子平均碰撞时间，τMW为振动松驰时间，τP为高温修正项。

由Landau-Teller理论结果给出

Millikan和White［17］在高温激波管内通过干涉仪观测了气体分子振动松驰过程，在104K的温度范围内，给出了如下拟合参数

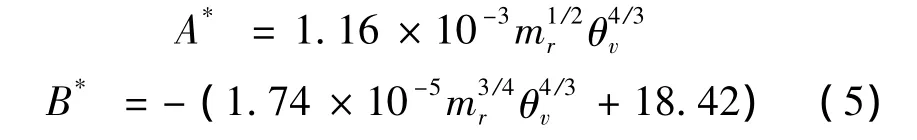
式中:mr为分子折合质量，θv是振动特征温度。Park［18］给出了高温修正的 τP为

式中:n是数密度，σv是分子振动碰撞截面(=10－20m2)，¯c是分子平均热运动速度。

1．3化学反应模型及非弹性碰撞模拟策略

通常反应速率常数可以写成下面的方程形式:

式中:Ea是反应中需要的活化能，k是Boltzmann常数，Λ和η是常数，由实验定出。

化学反应几率可以推导为下面的表达式［10］

式中:ε是对称因子，对于不同类分子ε=1，对同类分子ε=2。¯ξ为碰撞分子的平均内自由度，ωAB为碰撞对的粘性温度指数。当碰撞中的总碰撞能量Ec＞Ea时，反应截面σR与总碰撞截面σT的比值就是反应发生的概率，这种化学反应模型也称为TCE(Total Collision Energy)模型。

在DSMC模拟过程中为简化碰撞算法，假设非弹性碰撞的化学反应过程和内能交换是相互独立的事件。由于碰撞分子发生化学反应的几率在所有非弹性碰撞事件中是最低的，所以首先判断其是否发生化学反应。离解反应、交换反应等不同的化学反应过程在满足反应几率的条件下都有可能发生。在无法获知反应分子遵循何种反应轨迹生成新的反应生成物时，可以假定每种反应过程都是独立的。对所有可能发生化学反应的几率求和得到总的反应几率，如果Pr＞Rf，碰撞分子发生化学反应［19］。具体发生的是何种反应类型，则同样根据几率/Pr与随机数Rf的比较来选取，然后按照相应的化学反应类型产生新的生成物(分子或原子)。

对于不发生化学反应的碰撞分子，即Rf＞Pr时，则根据分子振动抽样概率，判断是否发生振动自由度的激发;对于未发生振动激发的分子，再根据分子转动抽样概率，判断是否发生转动自由度的激发;对于发生内自由度激发的分子，按相应的能量交换模型进行能量的再分配，否则分子按弹性碰撞处理。

由于本文模拟的高度较高，仅考虑五组元空气(O2，N2，O，N，NO)的离解反应和交换反应，烧蚀的影响暂不作考虑。

1．4 DSMC并行算法

DSMC并行算法采用区域分解的策略，根据计算的处理器数(或CPU核心数)的多少将计算区域划分为等量的子区域，每个处理器在其分配的子区域内部独立地计算模拟分子的碰撞和迁移，离开子区域的模拟分子把携带的信息传递给对应子区域的处理器。并行计算总的时间包括每个处理器计算碰撞、迁移的时间、处理器之间的通讯时间以及各处理器之间为同步而等待的时间。提高并行计算的效率主要是通过减少通讯和同步等待的时间来实现。

为了减少不同处理器计算时间的差别，通常采用负载平衡技术［20－22］，本文采用静态随机负载平衡方法用于解决不同处理器之间的计算时间同步问题［12］，该方法基于概率近似原理，将计算区域的全部网格平均分配给指定的所有处理器。由于采用相同的概率随机选取流场网格，按照均分后的数量分配给每个处理器，因此当计算区域的网格数量较多时，每个处理器包含近似相等的物体边界、高密度流动区域和稀薄气体区域的网格数，这样每个处理器的计算负载也非常接近。

2 计算结果分析

本文选取天宫一号目标飞行器的简化模型作为研究对象，飞行器上的太阳翼帆板朝向考虑两种情况，分别是板面平行于和垂直于飞行器中心轴线。计算的来流速度为7．6 km/s，高度范围为120 km～90 km，每隔10 km一个状态，攻角(Angle of Attack，AOA)为0°和20°，壁面温度设置为500 K、壁面反射模型为Maxwell模型(80%的漫反射、20%镜面反射)，仅计算对称的半个流场，计算中考虑了分子的转动、振动能量激发，90 km高度时还考虑了五组元空气的离解反应和交换反应。

2．1太阳翼帆板平行于目标飞行器

图2给出了太阳翼帆板平行于天宫一号目标飞行器情况下，0°攻角下不同再入高度时的压力等值线分布云图。从图中可以看出120 km、110 km高度的大气密度相对较低，尽管飞行速度达到了7．6 km/s，但飞行器的头部并未形成明显的脱体激波，而是逐渐增强的压缩过程，气体在整个太阳翼帆板的侧面也产生明显的压缩。图中也显示出，飞行器头部简化的对接机构形状对飞行器前方压缩气流的扰动影响，而随着飞行高度的降低，这种影响不断减弱，直至形成较强的头部脱体激波。100 km和90 km的头部激波作用在太阳翼帆板上产生了比驻点值高几倍的峰值压力和峰值热流。

图2 太阳翼水平放置时0°攻角不同高度压力分布Fig．2 Pressure distribution of 0°AOA in different altitude with horizontal solar array

图3给出了120 km和90 km在20°攻角下的压力分布云图。图中显示出，由于攻角的存在，除了在飞行器的头部产生压缩以外，整个飞行器舱体的迎风面也会产生较强的压缩，使舱体和太阳翼帆板的迎风受力面增大，作用在太阳翼帆板上的力和力矩都有较大增加。

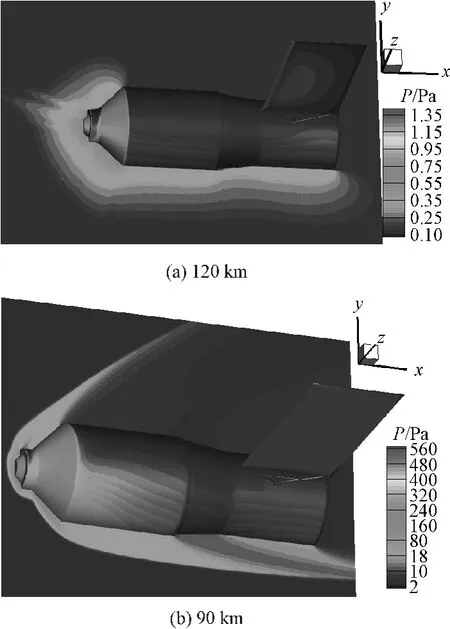
图3 太阳翼水平放置时20°攻角不同高度压力分布Fig．3 Pressure distribution of 20°AOA in different altitude with horizontal solar array

表1、表2分别给出了0°攻角和20°攻角不同高度情况下，作用在单侧太阳翼帆板上的轴向力、偏航力矩和峰值压力、峰值热流。由于太阳翼帆板平行于轴向方向，0°攻角时只有帆板的侧面为主要受力面，因此作用在帆板上面的轴向力和偏航力矩(力矩作用点取帆板与舱体的连接处)相对较小，但在100 km和90 km由于头部激波的干扰作用，使干扰区域的峰值热流非常高，100 km时的峰值热流为150 kW/m2左右，而到90 km时则达到了1．2 MW/m2。20°攻角时，尽管作用在帆板上的峰值压力和峰值热流与0°攻角时相差不大，但作用的轴向力和偏航力矩明显增大。因此，当太阳翼帆板平行放置时，激波干扰引起较强的气动加热可能最先破坏太阳翼帆板的结构，然后才是在气动力的作用下将其撕毁并脱离飞行器舱体。

表1 作用在水平太阳翼上的气动力和热流峰值(0°攻角)Table 1 Aerodynamics and peak heat flux acting on horizontal solar array at 0°AOA

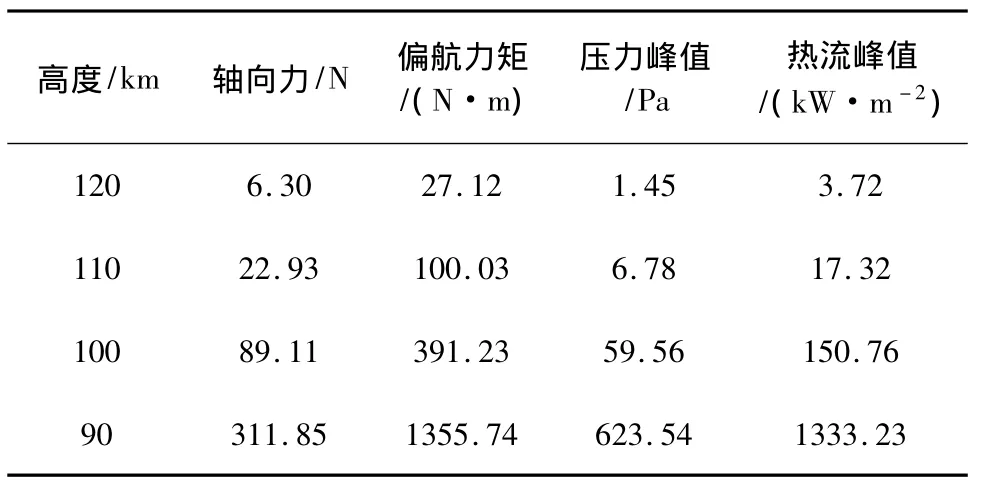
表2 作用在水平太阳翼上的气动力和热流峰值(20°攻角)Table 2 Aerodynamics and peak heat flux acting on horizontal solar array at 20°AOA

2．2太阳翼帆板垂直于目标飞行器

图4给出了太阳翼帆板垂直于目标飞行器0°攻角、不同再入高度时的压力等值线分布云图。图中显示出的流场结构与图2相似，只是此时太阳翼帆板有较大的迎风面，其前方的压缩层更厚(120 km、110 km)，激波/激波、激波/边界层的干扰更强、更复杂(100 km、90 km)，同时也与舱体产生了较强的相互作用，该区域的激波干扰使资源舱表面的压力和热流上升，尤其是在太阳翼帆板与舱体的连接处附近，更容易使太阳翼帆板遭到破坏，另外作用在帆板上的力和力矩明显比水平放置时大得多，因此垂直放置的太阳翼帆板会比水平放置的太阳翼帆板更早地在气动力、气动热的作用下被撕裂并脱离飞行器舱体。

图5给出了90 km高度、0°攻角下的压力等值线分布，可以更加详细地分析复杂激波干扰下的流动特征。头部脱体激波与太阳翼帆板的脱体激波相互作用并产生一道正激波对帆板表面形成非常强烈的压缩，使压力急剧上升。而在舱体表面附近区域，由于气体的膨胀，压力迅速下降，因此在头部脱体激波、舱体和太阳翼帆板表面之间的空域形成较大的逆压梯度，引起流动分离，同时产生的分离激波也与头部脱体激波相互干扰。图中还可以看出，从形成的正激波作用在帆板表面的位置开始，沿帆板左右各形成一股“喷流”，朝向舱体的“喷流”在较大的压力梯度下加速至超声速并直接撞击在资源舱的表面，形成局部的脱体激波。由于在较大的区域存在着逆压梯度，形成一个大的分离涡，而在帆板脱体激波影响的区域仅有微弱的流动分离，如图6所示。

图4 太阳翼垂直放置时0°攻角不同高度压力分布Fig．4 Pressure distribution of 0°AOA in different altitude with perpendicular solar array

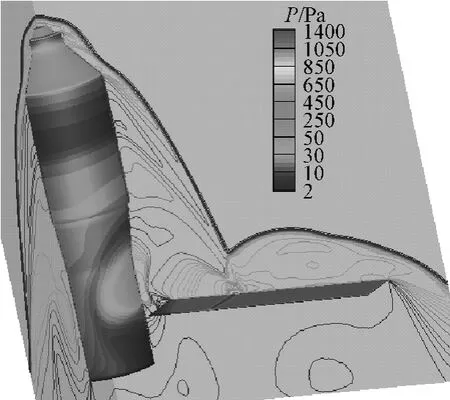
图5 90 km、0°攻角的压力等值线分布Fig．5 Pressure contours distribution of 90 km at 0°AOA

图7、图8分别给出了90 km高度、0°和20°攻角下的太阳翼帆板表面的压力和热流分布的对比，0°攻角作用在帆板表面的高压力和高热流区域近似为条状，而20°攻角时则近似为弧形，并且0°攻角时作用在帆板上的压力和热流强度高于20°攻角情况。从表3和表4给出的作用在帆板上的力和力矩表明，两种攻角下的力和力矩相差并不明显。在相同高度，作用在帆板的力和力矩要比水平放置时大一个量级。尽管100 km高度帆板表面的峰值热流比帆板水平放置时有较大降低，但由于100 km高度时太阳翼帆板所受的力和力矩是帆板水平放置时在90 km高度时的近3倍，超过了600 N和2700 N·m，到90 km时更是达到了3950 N和17000 N·m。因此太阳翼帆板垂直放置时，在100 km高度就有可能在气动力、气动热的双重作用下被撕裂并脱离飞行器本体。

图6 90 km、0°攻角的流线分布Fig．6 Stream lines distribution of 90 km at 0°AOA

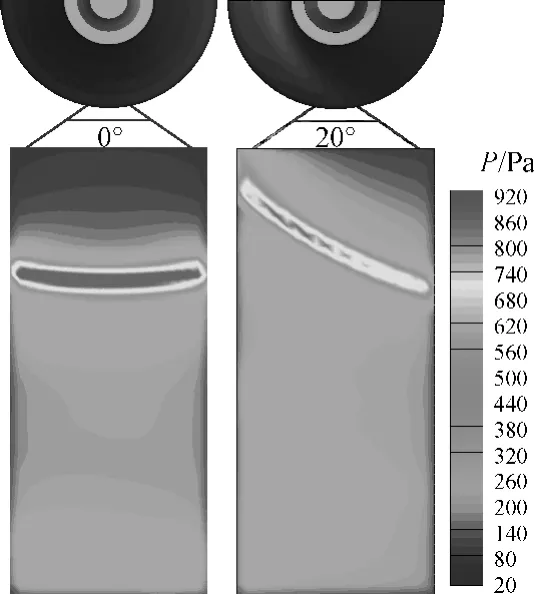
图7 太阳翼帆板表面压力分布Fig．7 Pressure distribution of solar panels surface

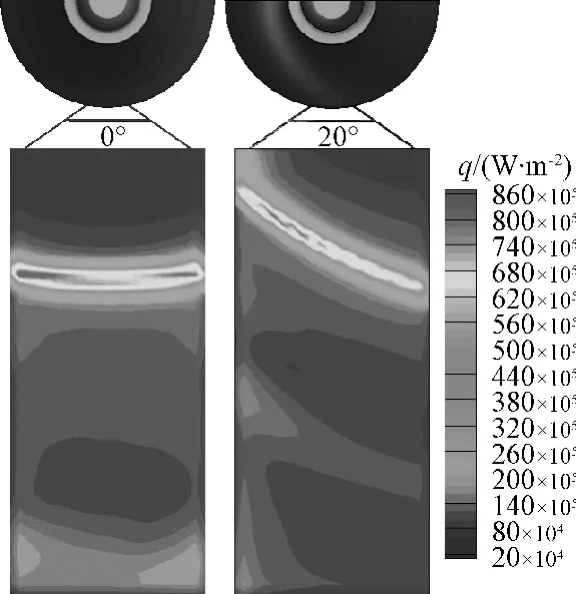
图8 太阳翼帆板表面热流分布Fig．8 Heat flux distribution of solar panels surface

表3 作用在垂直太阳翼上的气动力和热流峰值(0°攻角)Table 3 Aerodynamics and peak heat flux acting on perpendicular solar array at 0°AOA

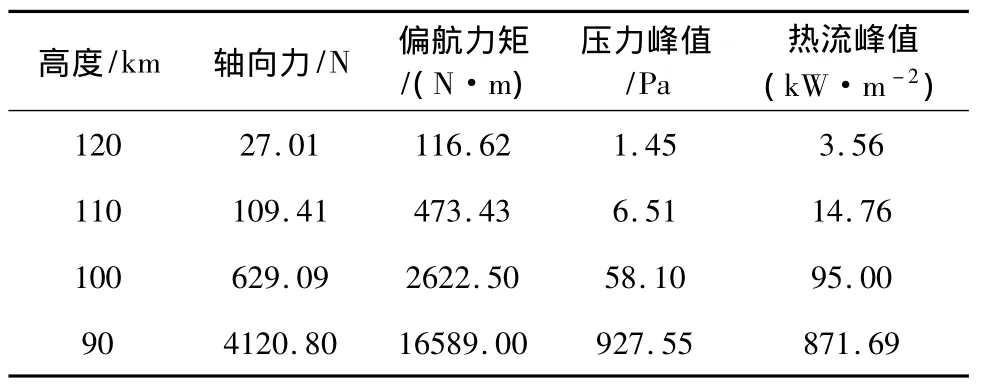
表4 作用在垂直太阳翼上的气动力和热流峰值(20°攻角)Table 4 Aerodynamics and peak heat flux acting on perpendicular solar array at 20°AOA

3 结论

通过上面的计算分析，得出以下几点初步结论:

1)100 km以上高度，来流气体对目标飞行器及太阳翼帆板是渐进的压缩过程，作用在太阳翼帆板上的力和力矩、峰值压力和热流相对较低。

2)100 km及以下高度，由于飞行器头部脱体激波与太阳翼帆板产生比较强的干扰，帆板所受的气动力、力矩以及表面上的峰值压力、热流随高度降低明显增大，且增大的速率加快。

3)太阳翼帆板水平放置时，激波干扰引起的侧缘峰值热流达到了兆瓦量级，较高的气动加热可能最先引起帆板结构的破坏，然后在气动力的共同作用下将其撕毁并脱离飞行器本体。

4)太阳翼帆板垂直放置时，飞行器头部脱体激波与帆板脱体激波产生更强烈、更复杂的激波/激波、激波/边界层的干扰。在相同高度，作用在帆板上的气动力和力矩要比水平放置时大一个量级，因此太阳翼帆板垂直放置时要比水平放置时更快地在气动力、气动热的双重作用下被撕裂并脱离目标飞行器。

［1］ 朱鲁青．美国“高层大气研究卫星”陨落事件分析［J］．国际太空，2011，11:27－33．［Zhu Lu-qing．Analysis of UARS reentry event［J］．Space International，2011，11:27－33．］

［2］ 都亨，张文祥，庞宝军，等．空间碎片［M］．北京:中国宇航出版社，2007:1－128．

［3］ 吴连大，王昌彬．危险目标再入跟踪预报研究［J］．紫金山天文台台刊，2000，19(2):100－105．［Wu Lian-da，Wang Chang-bin．Research on tracking and prediction of risk object reentry［J］．Publications of Purple Mountain Observatory，2000，19(2):100－105．］

［4］Opiela JN，Hillary E，Whitlock D O，et al．DASuser's guide［R］．Houston:Orbital Debris Program Office in NASA Johnson Space Center，TX，2007

［5］Bouslog SA，Ross B P，Madden C B．Space debris reentry risk analysis［R］．AIAA 1994－591，1994．

［6］Fritsche B，Klinkrad H，Kashkovsky A，et al．Spacecraft disintegration during uncontrolled atmospheric re-entry［J］．Acta Astronaut，2000，47(2－9):513－522．

［7］Wu Z N，Hu R F，Qu X，et al．Space debris reentry analysis method and tools［J］．Chin J．Aeronaut，2011，24:387－395．

［8］Li JL，Yan SZ．Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit［J］．Applied Thermal Engineering，2014，71:419－432．

［9］Li JL，Yan SZ，Cai R Y．Thermal analysis of composite solar array subjected to space heat flux［J］．Aerospace Science and Technology，2013，27(1):84－94．

［10］Bird G A．Molecular gas dynamics and the direct simulation of gas flows［M］．Oxford:Clarendon Press，1994．

［11］ 黄飞，赵波，程晓丽，等．返回器高空稀薄气动特性的真实气体效应研究［J］．宇航学报，2014，35(3):283－290．［Huang Fei，Zhao Bo，Cheng Xiao-li，et al．Real gas effects of reentry vehicle aerodynamics under hypersonic［J］．Journal of Astronautics，2014，35(3):283－290．］

［12］ 梁杰，阎超，杨彦广，等．过渡区侧向喷流干扰的并行DSMC数值模拟研究［J］．宇航学报，2011，32(5):1012－1018．［Liang Jie，Yan Chao，Yang Yan-guang，et al．Parallel DSMC simulation of lateral jet interaction in rarefied transitional region［J］．Journal of Astronautics，2011，32(5):1012－1018．］

［13］ 梁杰，阎超，杜波强．基于两级直角网格结构的三维DSMC算法研究［J］．空气动力学学报，2010，28(4):466－471．［Liang Jie，Yan Chao，Du Bo-qiang．An algorithm study of three-dimensional DSMC simulation based on two-level Cartesian coordinates grid structure［J］．Acta Aerodynamica Sinica，2010，28(4):466－471．］

［14］ 梁杰，阎超，李志辉，等．稀薄过渡流区横向喷流干扰效应数值模拟研究［J］．空气动力学学报，2013，31(1):27－33．［Liang Jie，Yan Chao，Li Zhi-hui，et al．Numerical investigation of lateral jet interaction effects in rarefied transition flow regime［J］．Acta Aerodynamica Sinica，2013，31(1):27－33．］

［15］Lumpkin F E，Hass B L，Boyd I D．Resolution of differences between collision number definition in particle and continuum simulations［J］．Physics of Fluids，1991，A3:2282－2284．

［16］Parker J G．Rotational and vibrational relaxation in diatomic gases［J］．Physics of Fluids，1959，2(4):449－462．

［17］Millikan R C，White D R．Systematics of vibrational relaxation［J］．The Journal of Chemical Physics，1963，39(12):3209－3213．

［18］Park C．Problems of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles［C］．Progress in Astronautics and Aeronautics，AIAA，New York，USA，Jule9－14，1985:511－537．

［19］Gimelshein N E，Gimelshein S F，Levin D A，et al．Reconsideration of DSMC models for internal energy transfer and chemical reactions［C］．23rd International Symposium of Rarefied Gas Dynamics，Whistler，Canada，July 20－25，2002:349－357．

［20］Ivanov M，Markelov G，Taylor S，et al．Parallel DSMCstrategies for 3D computation［C］．Proc．Parallel CFD’96，Capri，Italy，July 13－16，1996:485－492．

［21］LeBeau G J．A parallel implementation of the direct simulation Monte Carlo method［J］．Comput．Methods Appl．Mech．Engrg．1999，174:319－337．

［22］Wu J S，Tseng K C．Parallel DSMC method using dynamic domain decomposition［J］．Int．J．Numer．Meth．Engng．2005，63:37–76．