考虑重力影响的柔性关节空间机械臂任务空间神经网络控制
刘福才,高静方,贾晓菁
(燕山大学工业计算机控制工程河北省重点实验室,秦皇岛066004)
0 引言
空间机械臂作为太空的重要工具,是我国进一步发展空间技术,实现空间站建造、运营、维修及拓展过程中不可或缺的关键设备之一。实际系统的机械臂关节处在外界载荷作用下产生复杂的微观力学现象,导致关节机构的力学表现出强烈的非线性特征。空间机器人模型中存在关节柔性,这种现象在具有谐波传动装置的空间机械臂中尤其明显,即使采用行星齿轮驱动部件的空间机械臂,仍会表现出相当大的关节柔性影响。柔性关节会给控制系统带来滞后、非线性耦合和高频谐振等问题[1];Good等[2]通过实验发现关节柔性是设计机器人高精度轨迹跟踪控制器的障碍;Cetinkunt等[3]通过实验证明,忽略柔性关节影响设计的控制器在实际应用时存在问题,可能导致系统失稳。
目前很多文献针对柔性关节机器人进行了控制研究,主要的控制方法有奇异摄动方法、反馈线性化方法、无源性设计方法、级联系统法和反步法等,采用的是关节空间控制器设计的方案[4-6]。文献[4]对柔性关节控制提出了非线性解耦方法,给出了全局线性化的变换方程;文献[5]基于反步法设计了自适应模糊控制器,并通过实验证实具有良好的跟踪效果。这些控制器中需要计算动力学模型中惯性矩阵的逆,计算复杂;文献[6]基于无源性理论为柔性关节机器人设计了控制器,具有算法简单、有效减小力矩抖动和稳态精度高的优点,但加减速过程中跟踪误差较大。
机器人末端位置定义在任务空间,而关节空间的控制方案并不反馈末端执行器在任务空间中的位置和速度,实质上是一种开环控制。并且关节空间控制器局限于必须通过运动学逆解获得关节空间的控制量。一些学者对机器人任务空间控制进行了研究[7-9],文献[7]为自由漂浮空间机器人设计了基于神经网络的鲁棒智能控制器;文献[8]为机器人设计了任务空间自适应神经网络控制器。这些控制方法有良好的控制效果,但忽略了柔性关节影响。文献[9]对柔性关节模型进行了深入研究,采用基于奇异摄动的控制方法,为任务空间的柔性关节空间机器人设计了改进的简单自适应控制器(MSAC),但是并没有考虑重力对空间机械臂控制的影响。
应用于空间作业的柔性关节机器人首先要经历地面装调的阶段,文献[10]提到,虽然地面装调可在人为模拟的微重力环境下进行,但目前的技术仍无法进行长时有效的微重力环境模拟。利用自由落体及飞机抛物线飞行只能进行短时微重力环境模拟,水槽、悬吊、气浮等手段模拟的真实性较差,因此提出了采用运动行为模拟代替环境模拟的概念。考虑重力变化影响的空间机械臂控制已有一定的研究,文献[11]针对这种环境变化因素采取了神经网络自适应控制算法,使控制器能够适应环境的变化,采用神经网络的算法避免了一般自适应算法中回归矩阵的计算;文献[12]在此基础上考虑了系统的外部扰动问题,并设计了自抗扰控制器能够获得良好的跟踪效果;文献[13]针对系统扰动设计了滑模控制器,抖动抑制能力强,具有很强的鲁棒性。但是这些文献并没有考虑柔性关节的影响,模型过于理想;而且在控制上都采用了基于关节空间的控制方案,理论上没有任务空间控制效果好。因此,本文将重力项视为系统的不确定项,并考虑柔性关节影响,针对空间机械臂提出一种基于奇异摄动的任务空间神经网络自适应控制算法,用神经网络自适应算法对不确定项进行逼近。本文对于慢子系统采用基于任务空间控制的设计方法,即先将降阶系统转换到任务空间进行自适应神经网络控制器的设计,然后在设计好的控制器基础上左乘雅克比矩阵的转置,将力矩转换到关节空间,完成对慢子系统的设计。对于快子系统采用力矩反馈保证系统的稳定。
1 预备知识
1.1 RBF神经网络
RBF神经网络可以表示为:
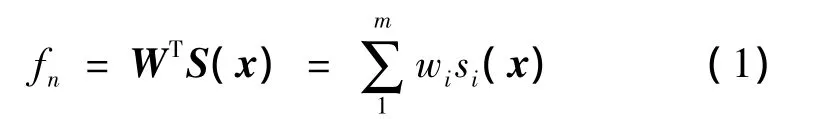
式中:m是节点数,x∈Ωx⊂Rn是网络的输入信号,si(x)(i=1,2,…,m)是径向基函数,W=[w1,…,wm]T∈Rm为神经网络权值。通常径向基函数选择为高斯函数:
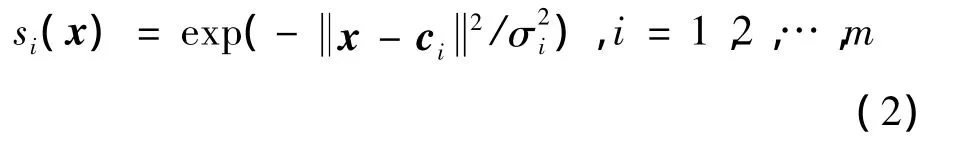
式中:ci为中心点,σi为基宽度。文中出现的向量范数均为2范数。
对于一个连续函数f(x),如果径向基函数确定,选取足够多的节点并适当构建基宽度和节点中心,RBF神经网络可以任意精度逼近该函数:
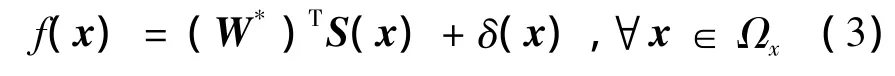
式中:W*表示对f(x)最佳逼近的权值矩阵,δ(x)为逼近误差。
RBF神经网络的局部特性表明,对于紧集Ωx中任意有界轨迹xξ(t),位于其局部区域内神经元仍可以以有限的数目逼近连续函数f(x)。
1.2动力学模型
第i个柔性关节示意图如图1所示。根据Spong的假设[14],柔性关节看作由电机和连杆及连接它们的弹簧阻尼系统组成,每个关节被看作是具有常值刚度的线性扭转弹簧,由此得到的柔性关节机械臂动力学包含两个二阶微分方程。qm∈Rn为电机轴角位移矢量,qr∈Rn是关节角位移矢量,弹性连接轴振动矢量定义为qr-qm。考虑关节柔性影响时,在动能项中加入转子的动能,并考虑柔性关节具有的弹性势能。
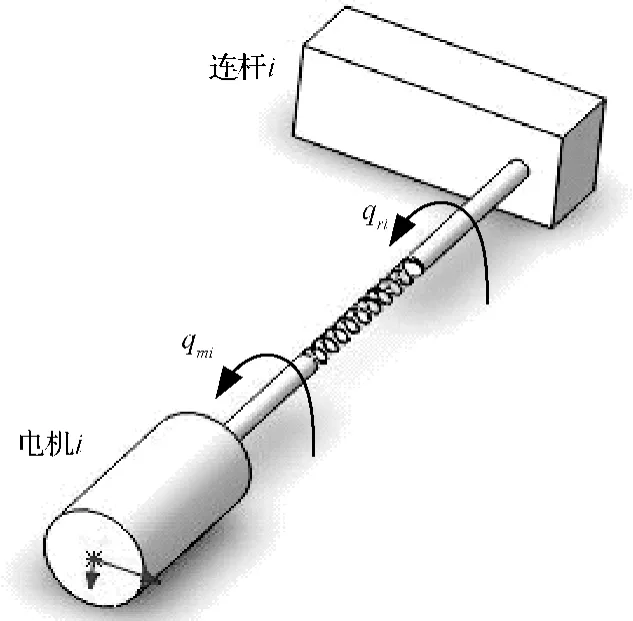
图1 柔性关节简化模型Fig.1 The map of the simplified flexible-joint model
在空间处于自由漂浮状态,依据拉格朗日方程对系统建模,可以得到载体位置、姿态均不受控时柔性关节空间机器人欠驱动形式的动力学方程如下:
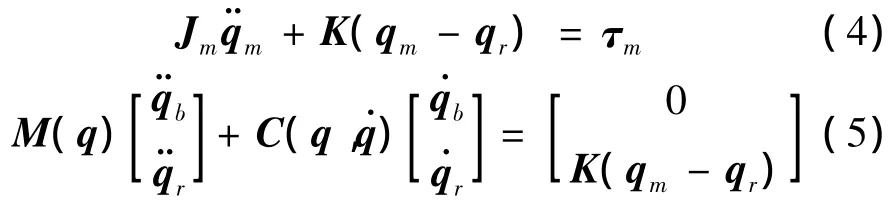
式中:Jm为电机转动惯量矩阵,具有正定对称性质,K为关节刚度系数矩阵,M(q)∈R(n+6)×(n+6)为系统的惯性矩阵为离心力和哥氏力矩阵,qb∈R6表示载体的位置和姿态,τm为电机输出的驱动力矩。利用动量守恒原理[15],可以推出完全驱动形式的动力学方程:
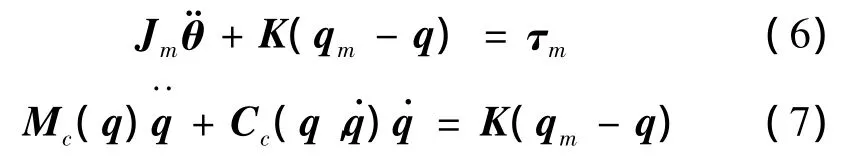
式中:Mc∈Rn×n,Cc∈Rn×n,q=qr∈Rn。空间机器人在地面进行模拟实验时,考虑重力的影响,柔性关节空间机器人从地面实验到空间阶段,动力学方程可以表示为如下形式:
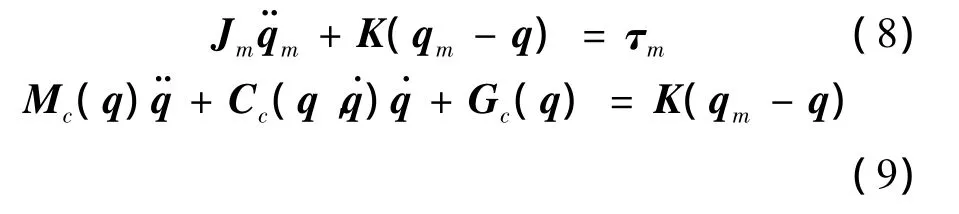
Gc因重力环境变化而变化,在这里视为不确定干扰量。在该模型中,杆的动力学和执行机构动力学通过弹性力矩项K(qm-q)耦合。
2 控制器设计与分析
2.1奇异摄动降阶处理
奇异摄动控制的思想是,将系统按时间尺度分解成快慢两个子系统,一般形式的非线性奇异摄动系统状态方程如式(10)所示,
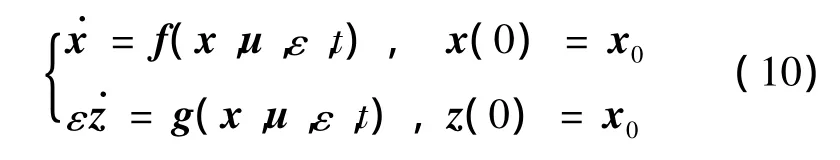
式中:ε为摄动参数。快子系统控制器设计时假设系统慢变量为常数;慢子系统设计时,令ε=0,忽略快子系统。如果慢、快子系统均是稳定的,则摄动参数比存在一个稳定上界,在此范围内,奇异摄动系统是稳定的。
基于奇异摄动方法,将柔性关节空间机器人进行快慢系统划分,分解为降阶系统和边界层系统。控制器分成两部分设计:

式中:τs是慢子系统控制量,τf是边界层系统控制量。
令
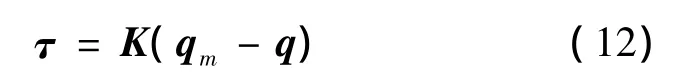
则τ实际为作用在机器人臂杆上的扭簧扭矩,由式(12)得到
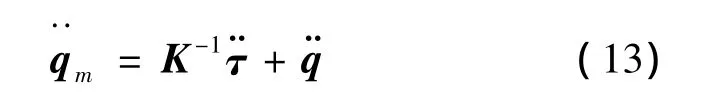
将式(11)~(13)代入式(8)中,得到
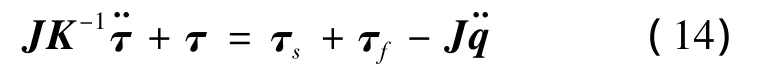
引入摄动参数 ε,取K=Kε/ε2,并选取 τf=,正定阵Kv为力矩反馈系数矩阵,代入上式的力矩方程中,得到边界层子系统为
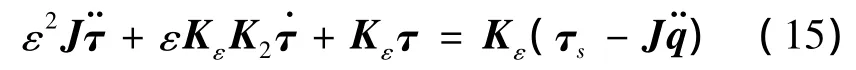
合理选取Kv的值以保证边界层系统的稳定。
令ε=0,将式(12)和(15)代入式(9)可以得到降阶后的子系统为:

式中:Dc(q)=Mc(q)+Jm(q)。
将降阶后的系统转换到任务空间,得到
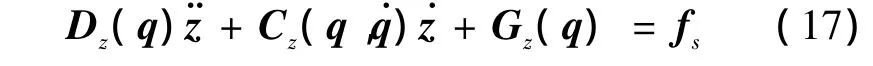
式中:Dz(q)=J-TDcJ-1,Gz(q)=J-TG,fs=J-Tτs,=J-TCcJ-1-Dz(q)˙JJ-1,z∈Rn为机器人工作空间的位置矢量,J∈Rn×n为雅克比矩阵。
动力学方程(17)满足下面性质:
性质1.矩阵Dz(q)对称正定且有界。
2.2神经网络控制器设计
定义滤波跟踪误差

根据式(17),将系统动力学方程写成如下形式
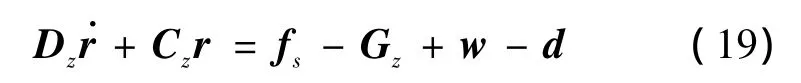
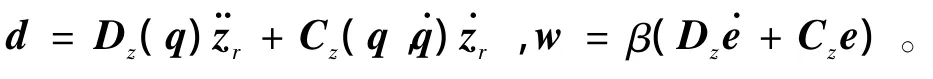
设计神经网络自适应控制器为
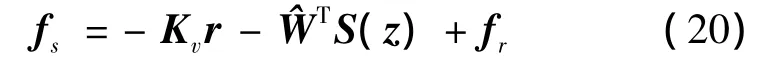
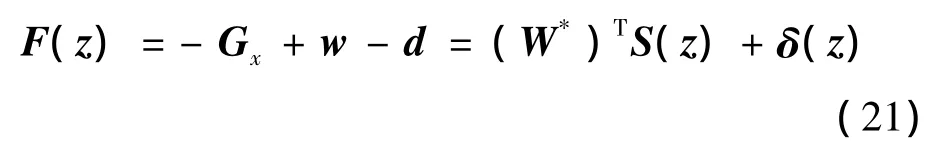
设 δ(z)≤ρ,fr是对神经网络建模误差的鲁棒补偿项
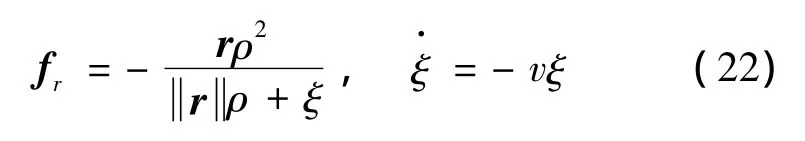
式中:v>0,ξ>0。
将式(20)和(21)代入式(19)中,得到
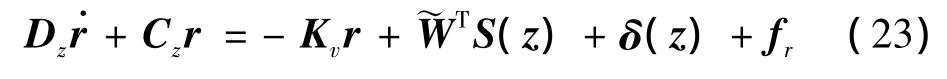
设计自适应律为

选取李亚普诺夫函数
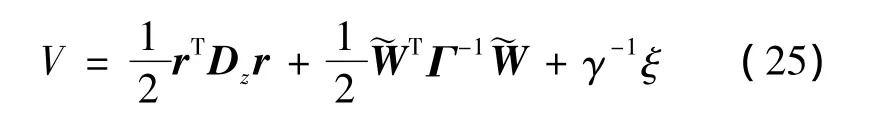
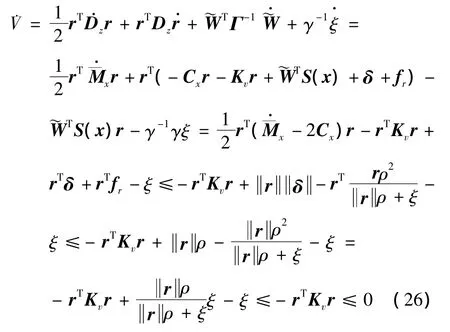
收敛性分析:
(1)由于Kv是正定矩阵,当且仅当即,根据LaSalle不变集定理,系统渐近稳定,当t→∞ 时
(2)由于V˙≤-rTKvr≤0,对于∀t≥0可得到0≤V(t)≤V(0)。当V(t)∈L∞时即
将控制力矩转换到关节空间,最终得到
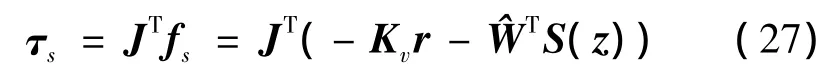
总的控制器为
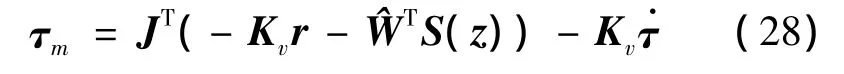
控制框图见图2。
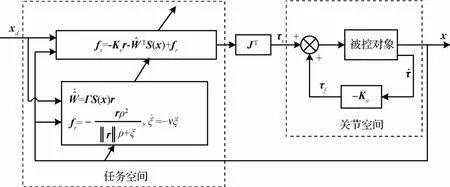
图2 柔性关节空间机器人系统任务空间控制框图Fig.2 The control block diagram of flexible-joint space robot in task space
3 仿真研究
对本文提出的两个阶段的模型进行了仿真研究,选择跟踪5 m×5 m的正方形轨迹。与其他类型的轨迹相比,如圆或直线,正方形轨迹跟踪对控制器要求更高,选择正方形轨迹可以观察在轨迹突变处的跟踪情况。表1为模型两个杆的仿真参数。

表1 平面二连杆柔性关节空间机械臂仿真参数Table 1 The parameters of two-link space manipulator
柔性关节模型参数:K=[500 0;0 500],Jm=[1 0;0 1]。控制器参数选择:Kv=diag(8,8),Γ=diag(8,8),β=2。
神经网络节点数N=7×7×7×7,分布区间分别为[-1.5 1.5]×[-1.5 1.5]×[-1.5 1.5]×[-1.5 1.5]。
为显示出神经网络自适应控制器的优良性能,与基于奇异摄动的任务空间PD控制进行了比较。图3和图4分别是PD控制在微重力和重力环境下的末端跟踪情况。
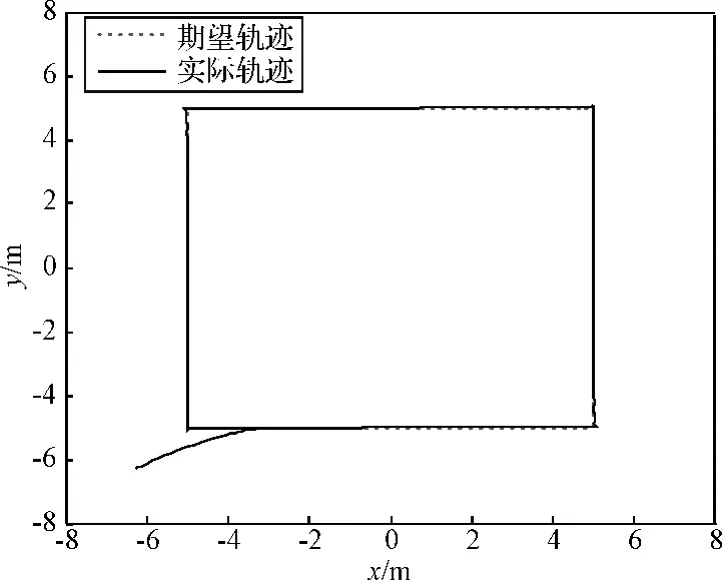
图3 微重力环境下的末端跟踪Fig.3 The tracking of the end in the micro-gravity environment
仿真结果表明,在微重力情况下机械臂实际轨迹可以跟踪上期望轨迹,但如果有重力影响,将达不到跟踪控制要求。并且,如果控制器中加入了重力补偿项,重力环境下虽然可以跟踪很好,但微重力环境下又无法准确跟踪,对于要实现轨迹跟踪高精度要求的空间机械臂来说,PD控制器无法满足要求。考虑重力影响的柔性空间机器人的轨迹跟踪对控制器有更强的性能要求。
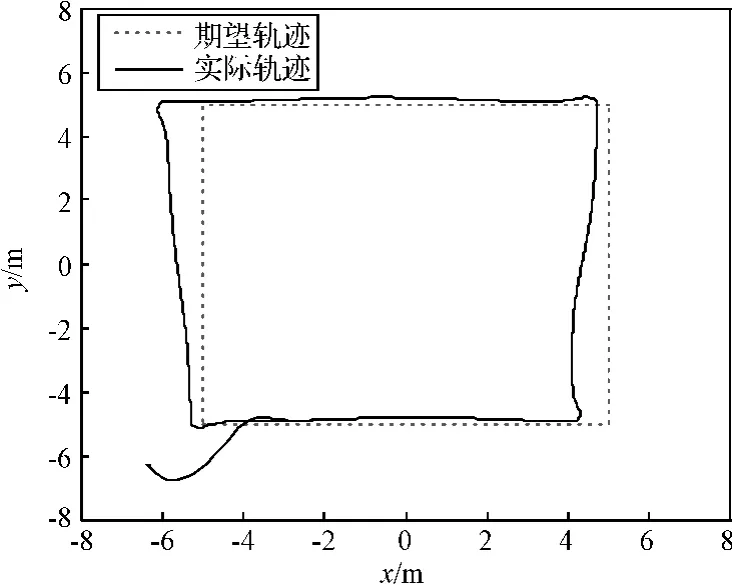
图4 重力环境下PD控制的末端跟踪Fig.4 The tracking of the end in the ground-gravity environment
采用任务空间神经网络自适应控制的仿真结果如下:
(1)地面重力情况下的仿真
重力加速度取g=9.8 m/s2,不确定函数的逼近结果采用f(·)范数表示。由图5(a)看出,柔性关节空间机器人在任务空间跟踪良好,可以很快跟踪上期望轨迹;由图5(c)可以看出,在每个正方形拐角处电机力矩突变,快速追踪改变方向轨迹;由图5(d)可以看出,神经网络对系统的不确定非线性项有较好的逼近结果。
(2)空间应用时的仿真
假设微重力情况下g=0 m/s2。由图6(a)看出,所提控制策略能够保证柔性关节机械臂末端执行器的实际轨迹快速地跟踪期望轨迹,由图6(b)可知,忽略拐角处的突变,跟踪误差可以快速收敛到0。
由图6(b)和图6(c)可知,在正方形每个拐角处轨迹发生突变,误差在瞬间增大,控制电机能够迅速调整输出力矩,使误差快速回到0;由图6(d)看出,微重力情况下神经网络对系统的不确定项仍有很好的逼近结果。由图5(c)和图6(c),通过对空间和地面电机驱动力的比较,可知在地面和在空间相同的轨迹跟踪所需的关节驱动力不同,在有重力的影响下,关节所需的控制力矩较大。并且由电机曲线可以看出系统在拐角处有轻微振荡,这是柔性关节带来的影响,而通过力矩反馈,振荡甚至不稳定现象已得到很强程度的抑制。
综上,通过以上两组仿真曲线可得,将重力等视为系统不确定项,所设计的神经网络自适应控制器可以很好地逼近,解决微重力环境下应用与重力环境调试的矛盾问题。

图5 地面重力影响下的仿真结果Fig.5 The Simulation results in gravity environment on ground
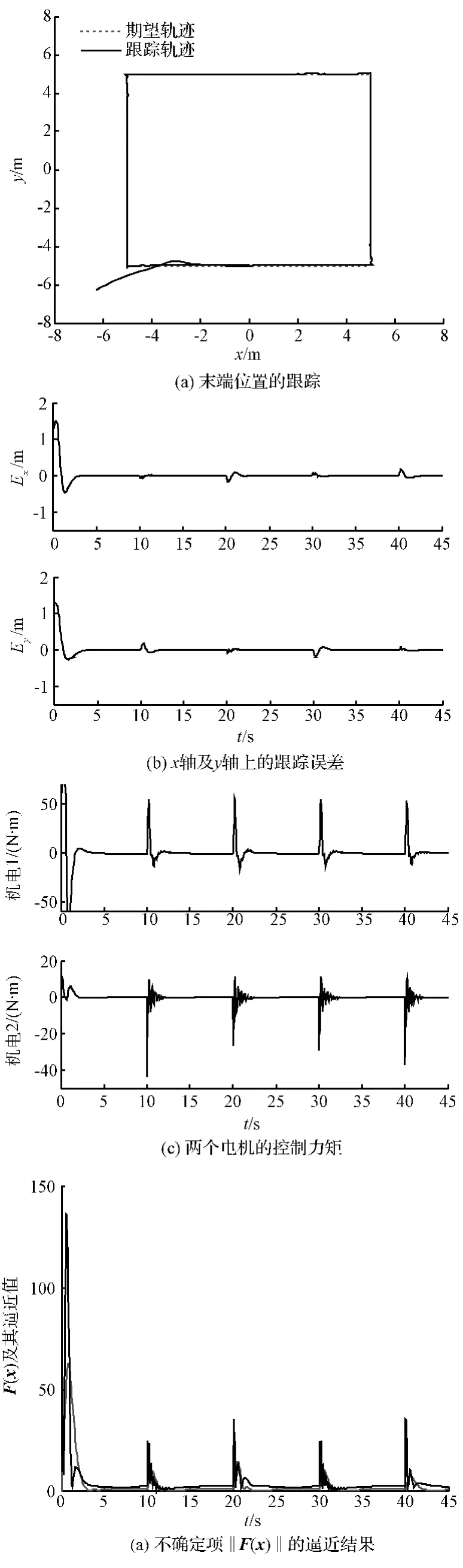
图6 微重力环境下的仿真结果Fig.6 The Simulation results in the micro-gravity environment
4 结论
本文建立了考虑重力影响的柔性关节空间机器人动力学模型,采用基于奇异摄动PD控制对两个阶段的轨迹跟踪进行了仿真研究,得出由于重力环境的不同,地面上适用的控制器到空间不一定可以跟踪上期望轨迹的结论,反之相同。提出一种基于奇异摄动的柔性关节空间机器人任务空间神经网络自适应控制策略,首先利用奇异摄动方法将系统分解为边界层系统和降阶系统,针对降阶系统,将重力视为系统的不确定项之一,采用RBF神经网络算法对不确定项进行逼近,对控制系统进行了收敛性分析。对有重力和微重力两种情况下柔性关节空间机器人的轨迹跟踪进行了仿真,结果表明,通过力矩反馈可以保证边界层系统的稳定,而降阶子系统不确定项也能够通过神经网络自适应算法得到准确估计,使控制系统不受环境变化的影响,能够获得高精度的轨迹跟踪。
[1] 邱志成,谈大龙.基于加速度反馈的柔性关节机械臂接触力控制[J].机械工程学报,2002,38(10):37-41.[Qiu Zhi-cheng,Tan Da-long.On acceleration sensor-based feedback control for contact force of the flexible joint manipulator[J].Chinese Journal of Mechanical Engineering,2002,38(10):37-41.]
[2]Good M,Sweet L,Strobel K.Dynamic models for control system design of integrated robot and drive system[J].Journal of Dynamic Systems,Measurement,and Control,1987,107(1):53-59.
[3]Cetinkunt S,Book W J.Flexibility effects on the control system performance of large scale robotic manipulators[J].Journal of the Astronautical Sciences,1990,3(4):531-556.
[4] 胡建元,王敏,黄心汉.柔性关节机器人非线性解耦控制[J].控制理论与应用,1996,13(3):366-370.[Hu Jian-yuan,Wang Min,Huang Xin-han.Nonlinear decoupling control for elastic-joint robot[J].Control Theory and Applications,1996,13(3):366-370.]
[5] 张晓东,贾庆轩,孙汉旭,等.空间机器人柔性关节轨迹控制研究[J].宇航学报,2008,29(6):1865-1870.[Zhang Xiao-dong,Jia Qing-xuan,Sun Han-xu,et al.The research of space robot flexible joint trajectory control[J].Journal of Astronautics,2008,29(6):1865-1870.]
[6] 张奇,谢宗武,刘宏,等.基于无源性理论的柔性关节控制器设计[J].机器人,2013,35(1):23-31.[Zhang Qi,Xie Zong-wu,Liu Hong,et al.Flexible joint controller design based on passivity theory[J].Robot,2013,35(1):23-31.]
[7] 丰保民,马广程,温奇咏,等.任务空间内空间机器人鲁棒智能控制器设计[J].宇航学报,2007,28(4):914-919.[Feng Bao-min,Ma Guang-cheng,Wen Qi-yong,et al.Design of robust intelligent controller for space robot in task space[J].Journal of Astronautics,2007,28(4):914-919.]
[8] 吴玉香,王聪.基于确定学习的机器人任务空间自适应神经网络控制[J].自动化学报,2013,39(6):806-815.[Wu Yu-xiang,Wang Cong.Deterministic learning based adaptive network control of robot in task space[J].Acta Automatica Sinica,2013,39(6):806-815.]
[9]Ulrich S,Jurek Z.Modeling and direct adaptive control of a flexible-joint manipulator[J].Journal of Guidance,Control,and Dynamics,2012,35(1):25-39.
[10] 王文魁.空间机构运动行为模拟概念研究[J].载人航天,2013,19(5):59-66.[Wang Wen-kui.Simulation study on motion behavior of spacecraft mechanisms[J].Manned Spaceflight,2013,19(5):59-66.]
[11] 刘福才,高娟娟,王芳.不同重力环境下空间机械臂神经自适应鲁棒控制[J].宇航学报,2013,34(4):503-510.[Liu Fu-cai,Gao Juan-juan,Wang Fang.Neural adaptiverobust control of space manipulator under different gravity environment[J].Journal of Astronautics,2013,34(4):503-510.]
[12] 刘福才,梁利环,高娟娟,等.不同重力环境的空间机械臂自抗扰轨迹跟踪控制[J].控制理论与应用,2014,31(3):352-360.[Liu Fu-cai,Liang Li-huan,Gao Juan-juan,et al.Trajectory tracking control with active disturbance rejection for space manipulator in different gravity environments[J].Control Theory and Applications,2014,31(3):352-360.]
[13] 刘福才,梁利环,秦利,等.考虑重力影响的空间机械臂轨迹跟踪滑模控制[J].控制与决策,2014,29(10):1856-1860.[Liu Fu-cai,Liang Li-huan,Qin Li,et al.Sliding mode control for space manipulator trajectory tracking considering effects of gravity[J].Control and Decision,2014,29(10):1856-1860.]
[14]Spong M W.Modeling and control of elastic joint robots[J].Journal of Dynamic Systems,Measurement,and Control,1987,109(4):310-319.
[15] 陈志勇,陈力.漂浮基带柔性铰空间机器人的动力学建模及奇异摄动控制研究[J].中国机械工程,2011,22(18):2151-2155.[Chen Zhi-yong,Chen Li.Study on dynamics modeling and singular perturbation control of free-floating space robot with flexible joints[J].China Mechanical Engineering,2011,22(18):2151-2155.]

