精密定轨中三类经验加速度的有效建模方法

王文彬，高 扬

(中国科学院空间应用工程与技术中心，北京100094)

0 引言

受太阳活动、地磁活动、季风等复杂因素影响以及大气密度、辐射光压、重力场等模型误差影响，很难建立地球低轨卫星高精度确定性动力学模型。目前确定性动力学模型还无法匹配GPS载波相位的测量精度(毫米级)［1－2］，所以地球低轨卫星若只采用确定性动力学定轨方法较难获得高精度的定轨结果。简化动力学定轨方法在确定性动力学模型的基础上引入经验加速度模型吸收未模型化动力学误差，使得简化动力学模型(包括确定性动力学模型和经验加速度模型)精度能够匹配GPS载波相位的测量精度，同时能够保持动力学模型对卫星轨道的约束作用，保证轨道解的稳定性。

目前存在三类典型的经验加速度模型:瞬时速度脉冲(Instantaneous Velocity Pulses，IVP)［2－5］、逐段常量经验加速度(Piecewise Empirical Accelerations，PEA)［1，6－8］以及周期性摄动加速度(Once－Per－Revolution Perturbations，OPRP)［9－10］。

1)瞬时速度脉冲定义在预先划分的时间历元上，只在有限个离散的历元上存在速度的突变，用于改变卫星速度状态，其他历元上速度是连续的。

2)逐段常量经验加速度定义在预先划分的时间段上，在任意时间段内经验加速度保持常量。方向分别为轨道径向、切向和法向，切向主要吸收大气阻力模型误差，法向吸收未模型化的地球反照光压误差、太阳辐射光压误差等［1］。

3)周期性摄动加速度模型利用轨道的周期性，假设未模型化动力学误差可用傅立叶级数的形式描述，每个轨道周期包括一组傅立叶级数系数。

利用瞬时速度脉冲来对动力学模型误差进行补偿，它的优点是模型简单，无需对含有瞬时速度脉冲参数的微分方程进行数值积分，但速度脉冲使卫星轨道速度精度下降，且在有限离散历元上不再连续。

瞬时速度脉冲和逐段常量经验加速度都称为伪随机参数模型，模型本身没有约束性，其值受GPS测量值的影响较大。优点是模型可以很好地匹配GPS测量值，当测量值的质量和精度较高时定轨精度和稳定性较高;缺点是当GPS测量值出现间断或频繁出现周跳时，定轨精度则较差(文献［1］对CHAMP和GRACE星载GPS数据存在间断的时段定轨表明精度为米级)。

周期性摄动加速度模型采用周期为一个轨道周期的傅立叶级数对未模型化动力学误差进行建模。该模型本身具有约束性，理论上受GPS测量值质量和精度的影响相对于伪随机参数模型要小，且待估参数较少。但有些误差明显不具有周期性，无法用该模型来描述，比如姿态误差引起的面质比变化等［2］。

经验加速度模型已在简化动力学最小二乘批处理中得到了广泛的应用［1，5－7，10－11］。在批处理过程中，伪随机参数模型的参数达到400～800个，敏感矩阵求解规模和数据存储量较大，同时由于GPS观测量多，法方程的构建时间较长。设计矩阵中包含大量敏感矩阵，若都通过数值积分得到，则计算量非常大。同时设计矩阵大致呈下三角形式，存在大量零元素，传统建模方法会使法方程构建过程增加大量重复或无效计算，且占用大量数据存储空间。

本文首先对三类经验加速度模型建模。根据不同模型的特点，分别给出敏感矩阵求解的有效方法，并定性比较该方法和传统方法的数值积分规模以及存储量。同时根据敏感矩阵求解式的特点，将参数改正方程组表示为分块子矩阵的形式，从而得到构建法方程的有效方法。然后将该方法扩展到基于GPS观测模型的最小二乘批处理定轨过程中。最后应用GRACE－A星载GPS观测数据对三种经验加速度模型的法方程构建效率进行测试与分析。

1 轨道动力学模型

卫星状态yT(t)=(rT(t)，vT(t))包括位置矢量r(t)和速度矢量v(t)，动力学方程表示为

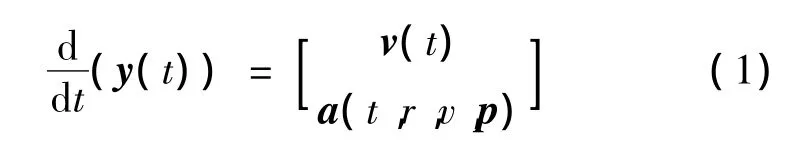
式中，a为地球卫星加速度矢量和，p为动力学参数。

y(t)关于初始状态y0(t)(y0=y(t0))的偏导数阵记为状态转移矩阵Φ(t，t0)，y(t)关于p的偏导数阵为敏感矩阵Sp(t)。它们的一阶微分方程分别为［12］:

和

式中:

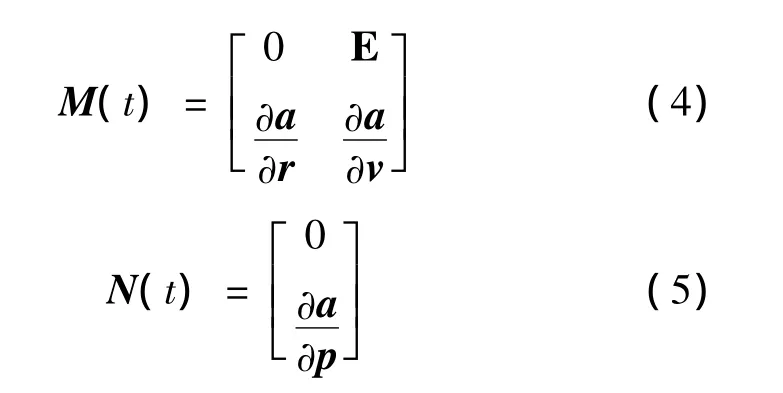
其中，E为单位矩阵。若设Φ(t，t0)为齐次微分方程组(2)的解，根据非齐次微分方程组解结构的一般理论［13］，式(3)的解可表示为

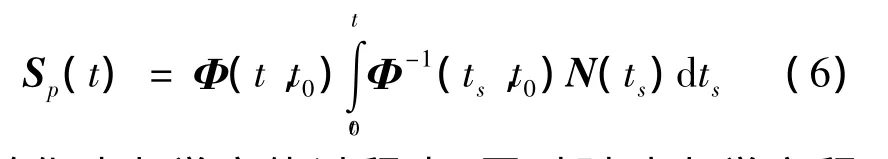
简化动力学定轨过程中，同时对动力学方程(2)和(3)微分方程和进行数值积分，可以得到任意时刻的卫星状态、状态转移矩阵和敏感矩阵，用于计算GPS测量值与模型值的残差、组成最小二乘参数估计法方程。

2 经验加速度建模

2．1瞬时速度脉冲

瞬时速度脉冲通过瞬时改变卫星速度的大小和方向来补偿确定性动力学模型误差，作用等同于在加速度上施加一个单位脉冲函数。设定子区间长度为τ，整个定轨时间区间［t0，tn］划分为nv段，瞬时速度脉冲vi=(viR，viT，viN)T作用在离散历元ti上(ti=t0+i·τ，i=1，…，nv－1)，viR viT和viN对应的方向分别为轨道径向eR(t)、切向eT(t)和法向eN(t)。

动力学方程需在确定性加速度模型a(t)的基础上增加瞬时速度脉冲项［8］:

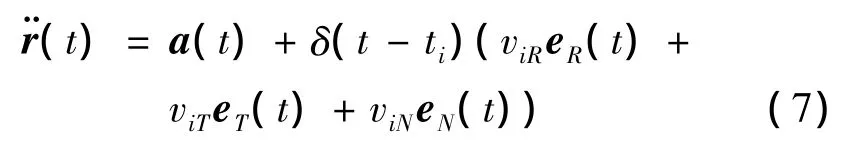
式中，δ(t)为单位脉冲函数。vi的敏感矩阵记为Svi(t)，根据式(6)，其可由下式计算

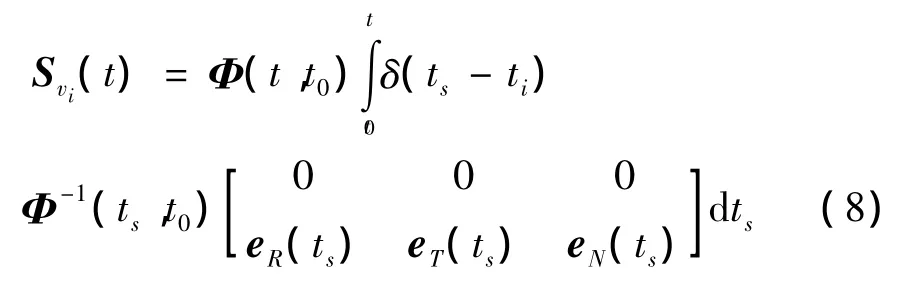
当t≥ti时，利用脉冲函数的性质，式(8)右端的积分项为常值矩阵，记为Pi，利用边值条件得到

此时Svi(t)表示为Φ(t，t0)和常值矩阵Pi(与i相关)的乘积。最终敏感矩阵的解为

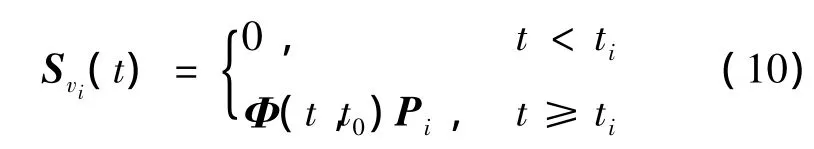
速度脉冲参数敏感矩阵的微分方程在除有限个点外是齐次的，敏感矩阵的计算无需数值积分。

图1给出的是与瞬时速度脉冲参数相关的敏感矩阵作用区域，“灰色”为非零区域，敏感矩阵可表示为状态转移矩阵和常值矩阵的乘积。传统方法需存储所有敏感矩阵，存储规模为O(nv2)，而对于敏感矩阵的有效计算方法，只需存储矩阵Pi(i=1，…，nv－1)即可，存储规模为O(nv)，该方法有效降低敏感矩阵的存储规模。

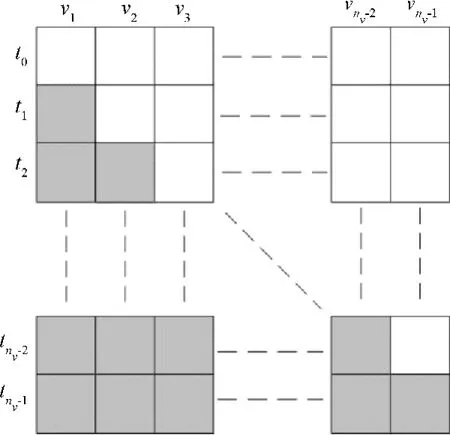
图1 与瞬时速度脉冲参数相关的敏感矩阵作用区域Fig．1 Activity areas of sensitive matrices related to instantaneous velocity pulses

下面给出瞬时速度脉冲模型的参数改正方程和法方程的矩阵分块建模方法。记zl、hl和εl分别为tl时刻的测量值、模型值和残差值，其中tl∈［ti，ti+1)，i=0，1，…，nv－1。假设动力学参数只包括初值状态和经验加速度参数(下同)，参数改正方程为

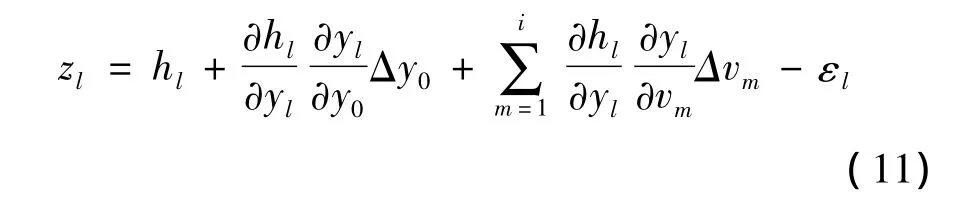
根据式(10)，上式进一步展开为

其中，bl=zl－hl，Pm由式计算。

若考虑［ti，ti+1)内所有观测量hi，参数改正方程组可表示为子矩阵的形式

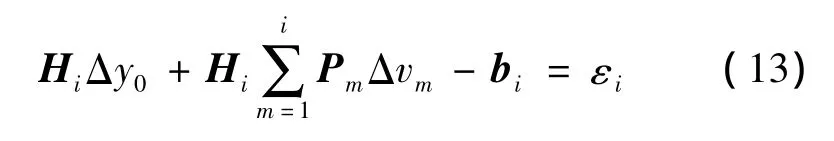
其中

若考虑［t0，tn)内所有观测量，参数改正方程组AvΔxv=bv可表示为分块子矩阵的形式，设计矩阵Av、Δxv和右端项bv分别为

和

最小二乘批处理法方程为

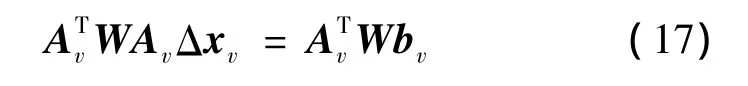
利用矩阵分块结构，法方程矩阵表示为

和

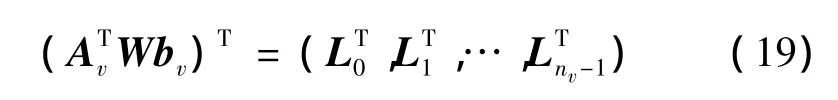
用矩阵分块方法构建法方程非常有效，且矩阵结构非常清晰:

1)法方程矩阵由Pi(与敏感矩阵相关)以及和(与状态转移矩阵相关)组成，i

3)Nmn由左乘，右乘Pn得到;Lm由左乘得到，m，n=0，1，…，n－1。v

2．2逐段常量经验加速度

整个区间［t0，tn］等间隔划分为na段，逐段常量经验加速度ai=(aiR，aiT，aiN)T在子区间［t0，tna］上保持常量(ti=t0+iτ，i=0，…，na－1)。ai的方向和瞬时速度脉冲模型一致。

同理，动力学方程表示为［8］:

其中

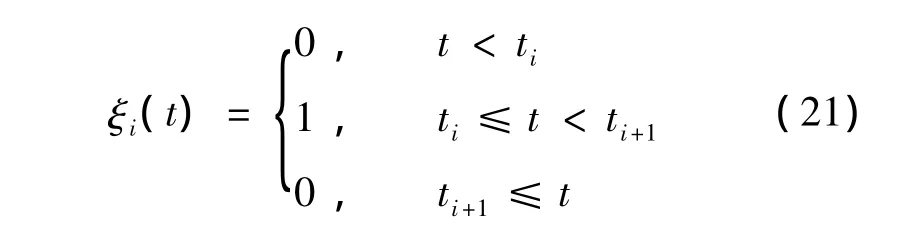
根据式(6)，敏感矩阵Sai(t)可表示为

当t≥ti+1时，式(22)右端的积分项为常值矩阵，记为Pi+1，其值由式(24)给出。即当微分方程为齐次时，Sai(t)可表示为和常值矩阵Pi+1(与i相关)的乘积。当ti≤t＜ti+1时，则按照微分方程

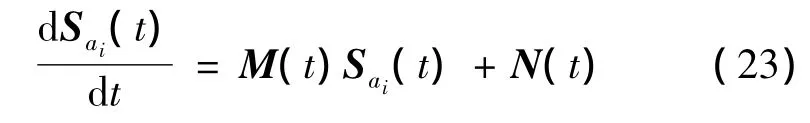
积分计算，初值条件Sai(ti)=0。因Sai(t)在整个区间上是连续的，故数值积分得到的Sai(ti+1)在ti+1时刻也可表示为Φ(ti+1，t0)与Pi+1的乘积，于是得到常值矩阵

综上所述，Sai(t)为

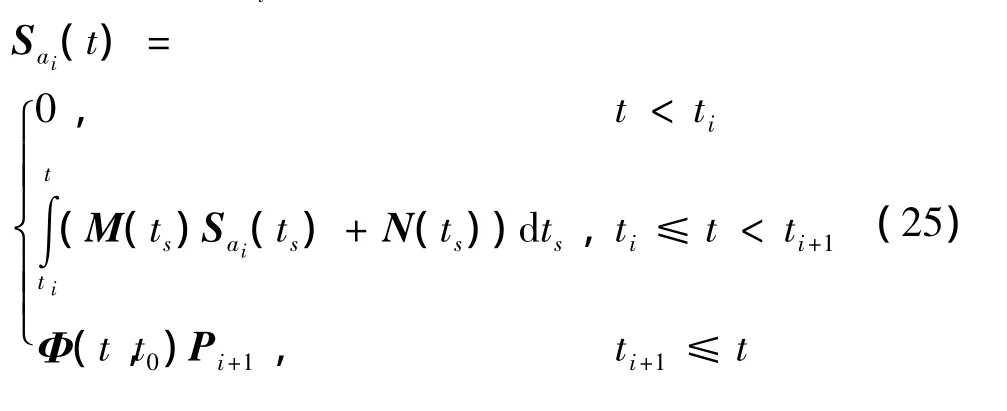
逐段常量经验加速度的敏感矩阵求解式相比瞬时速度脉冲式，多了数值积分项，这是导致敏感矩阵有效区域，参数改正方程以及法方程结构与瞬时速度脉冲参数模型存在区别的根本原因。

图2给出的是与逐段常量经验加速度相关的敏感矩阵有效区域。“灰色”区域的敏感矩阵可以表示为状态转移矩阵和常值矩阵的乘积，无需数值积分，“×”区域需进行数值积分，积分和存储规模为O(na)。而传统方法的数值积分区域包括所有“×”和灰色区域，积分和存储规模为O(na2)。

图2 与逐段常量经验加速度相关的敏感矩阵作用区域Fig．2 Activity areas of sensitive matrices related to piecewise empirical accelerations

逐段常量经验加速度的参数改正方程组也可表示为分块矩阵的形式

其中，i=0，1，…，na－1，Hi和Pm+1分别见式(14)和(24)。与瞬时速度脉冲不同，该式多出一项:

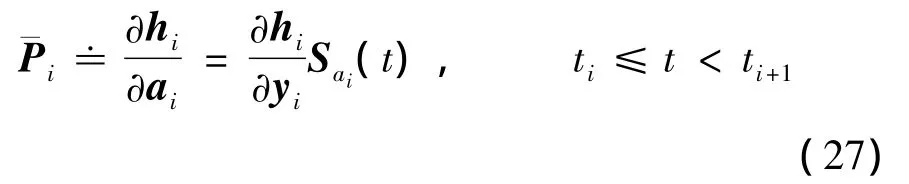
该项需要数值积分计算。

对于所有观测量，参数改正方程AaΔxa=ba表示为分块矩阵的形式，设计矩阵Aa和右端项ba分别为

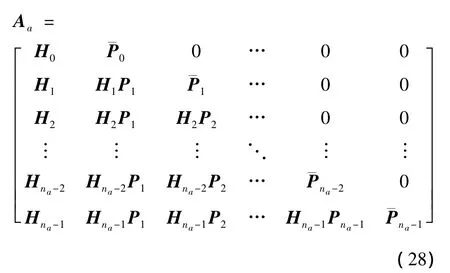
和

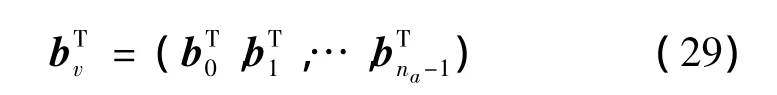
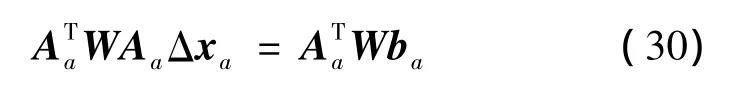
法方程为该矩阵表示为两个矩阵之和，第一个矩阵结构与瞬时速度脉冲模型一致，第二个矩阵与相关。设

其中

子矩阵Nmn和右端项Lm的定义分别与式(18)和(19)相同，m，n=0，1，…，na－1。

矩阵M2a和右端项b2a分别为

和

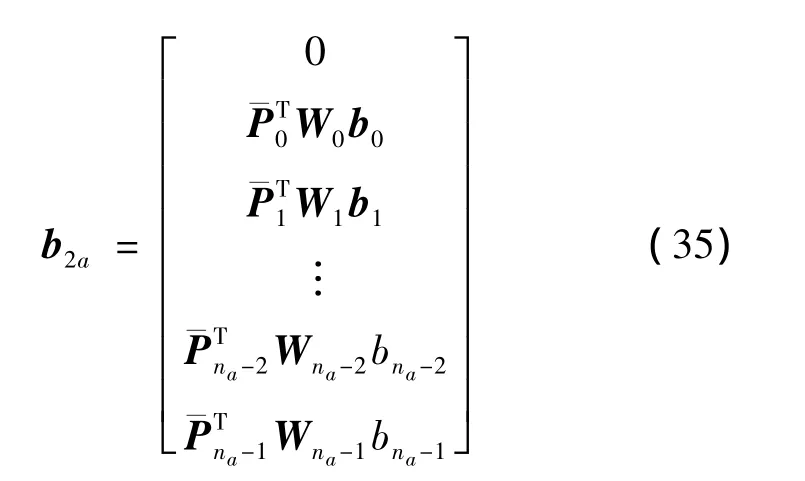
瞬时速度脉冲模型的法方程矩阵结构是逐段常量经验加速度模型的简化形式，程序设计中可考虑二者间的继承性。关于法方程构建效率的算例分析见第4节。

2．3周期性摄动加速度

周期性摄动加速度模型假设未模型化力具有周期性，可用傅立叶级数描述，相当于对未模型化力做了一种约束，自变量也从时间(t)变为升交角距(u(t))。

周期性摄动加速度模型参数(ciR，siR，ciT，siT，ciN，siN)T在预先定义的区间［ti，ti+1)保持常量(ti=t0+iT，i=0，…，ncpr－1)，T为一个轨道周期，方向与伪随机参数模型一致。动力学方程为

式中:

周期性摄动加速度模型的敏感矩阵计算方法、设计矩阵和法方程矩阵的分块结构与逐段常量经验加速度完全一致，不再赘述。一般周期性摄动加速度模型参数个数要明显少于伪随机参数模型，法方程构建效率的算例分析见第4节。

3 简化动力学最小二乘批处理

简化动力学最小二乘批处理方法(Batch Leastsquares，Batch LSQ)利用GPS非差消电离组合观测量定轨，测量模型包含接收机钟差以及模糊度参数，除了初始状态和经验加速度外，动力学参数还包括大气阻力系数(CD)和太阳辐射光压系数(CR)。

最小二乘批处理的法方程结构可见文献［7］，其中法方程中与动力学参数对应的矩阵计算量最大。对比上节，虽然动力学参数多了CD和CR两项，但矩阵分块的建模方法仍是有效的。只需形式上将这两个参数组合到式(13)和(26)的子矩阵Hi中［8］，记作

相应地，记

那么式(15)和(28)的分块矩阵中，Hi和Pi将分别被和所替代，法方程矩阵的结构没有发生改变。

4 经验加速度有效建模方法的计算效率分析

利用GRACE－A星载GPS载波相位和伪距观测数据，对应用在最小二乘参数估计过程中的三类经验加速度的建模效率进行测试。我们只分析矩阵分块建模方法与传统建模方法的计算效率，关于定轨精度分析由另文给出。

GRACE－A为低轨近圆轨道卫星，平均轨道高度460公里。GPS观测数据来自于美国宇航局JPL实验室物理海洋学数据分发存档中心(PO．DAAC)［14］，选取的日期为2006年1月3日;GPS精密星历以及钟差来自于欧洲轨道确定中心(CODE)［15］。解算设置为:批处理时长为一天(24小时)，数据采样间隔30秒。设置典型的区间长度τ:瞬时速度脉冲和逐段常量经验加速度模型为600秒(模型参数总数432个)，周期性摄动加速度模型为一个轨道周期(5662秒，参数总数94个)。选取两组实验数据，第一组只含有伪距观测量，第二组包含伪距和载波相位观测量。因为两类观测量的累加，使得观测量增加一倍的同时还引入了模糊度参数。

测试的笔记本电脑型号为Lenovo T430S，主频2．9 GHz，内存4Gbytes。

4．1伪距观测量

前文给出了关于经验加速度敏感矩阵的有效计算方法，已从数值积分计算规模和敏感矩阵存储规模的角度上做了定性分析。下面从法方程的构建上分析传统方法和矩阵分块方法的计算效率，不包括法方程逆矩阵求解。传统计算方法指不对参数改正方程(式和式)进行分块，直接利用设计矩阵相乘得到法方程矩阵。

2006年1月3日的消电离伪距观测量经预处理后的数目为21690个。因最小二乘批处理过程为数值迭代过程，每次迭代过程的计算量几乎相同，为简明起见只比较一次迭代的计算时间。

图3给出的是三种经验加速度模型的法方程构建计算时间对比，纵轴为CPU计算时间。同属于伪随机参数模型的瞬时速度脉冲和逐段常量经验加速度模型的计算时间比较接近，且明显高于周期性摄动加速度。伪随机参数模型的矩阵分块计算方法将计算效率提高了1倍，而周期性摄动加速度模型几乎没有提高。事实上，伪随机参数模型数目是周期性摄动加速度的4．6倍，待估参数越多，利用法方程子矩阵的递归关系减少重复计算的效果越明显，而周期性摄动加速度的参数少，计算效率的提升并不明显。

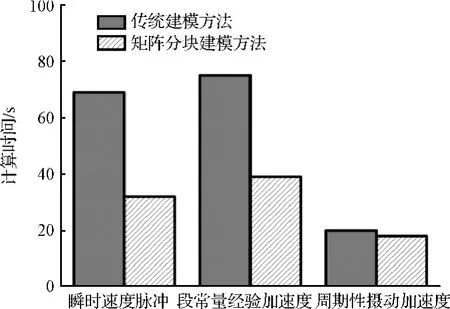
图3 三类经验加速度模型的法方程构建计算时间对比，观测量为GPS伪距消电离组合Fig．3 The computing time comparisons of setting up normal equations(without inversion)for three empirical acceleration models using pseudorange observations

4．2伪距加载波相位观测量

低轨卫星若实现厘米级精密定轨需求，一般采用伪距加载波相位作为观测量。预处理后的观测量数目为43380个，比只考虑伪距观测量多了一倍，且待估参数增加了模糊度参数(428个)，必然加大了法方程的构建时间。

图4为利用伪距加载波相位消电离组合观测量的法方程构建计算时间对比。相比于只利用伪距观测量(图3)，无论传统方法还是矩阵分块方法，计算时间增加约2～3倍。对于伪随机脉冲模型，矩阵分块建模方法将效率提高3．5倍，同样周期性摄动加速度建模的效率没有明显提高。

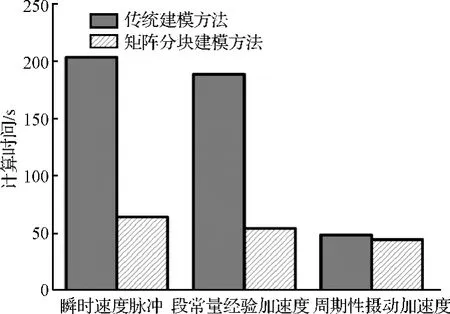
图4 三类经验加速度模型的法方程构建计算时间对比，观测量为伪距加载波相位消电离组合Fig．4 The processing time comparison of setting up normal equation(without inversion)for three empirical acceleration models

5 结论

本文介绍了地球低轨卫星精密定轨的三类常用经验加速度模型的有效建模方法，包括瞬时速度脉冲、逐段常量经验加速度以及周期性摄动加速度。因经验加速度模型参数一般较多，传统建模方法的敏感矩阵数值积分规模较大，且构建法方程的效率较低。

当经验加速度敏感矩阵的微分方程是齐次方程时(除有限历元或有限区间外)，敏感矩阵可表示为状态转移矩阵和某一常量矩阵的乘积(式(10)和式(25))。瞬时速度脉冲参数敏感矩阵无需通过数值积分计算，另外两类模型的敏感矩阵计算规模是O(n)(n为参数个数)，而传统方法的计算规模是O(n2)。在敏感矩阵的有效求解方法基础上，用分块子矩阵构建法方程效率会有明显提高。

利用GRACE－A星载GPS观测数据测试，在典型的精密定轨设置下，定量分析矩阵分块建模方法的法方程构建效率。观测量为伪距时，伪随机参数模型的效率提高1倍;观测量为伪距加载波时，效率提高3．5倍。观测量越多，待估参数越多，矩阵分块的建模方法越有效。周期性摄动加速度模型的构建效率没有明显提高，其参数数目明显小于伪随机参数模型。此外，逐段常量经验加速度和周期性摄动加速度模型的法方程是在瞬时速度脉冲模型的基础上增加了一个方程，建模方法具有继承性。

［1］Kroes R．Preciserelative positioning of formation flying spacecraft using GPS［D］．Delft:Delft University of Technology，2006．

［2］Beutler G，Jäggi A，Hugentobler U，et al．Efficient satellite orbit modelling using pseudo－stochastic parameters［J］．J．Geod．，2006，80(7):353－372．

［3］Beutler G，Brockmann E，Gurtner W，et al．Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics(IGS):theory and initial results［J］．Manuscr Geod，1994，19:367－386．

［4］Jäggi A，Hugentobler U，Beutler G．Pseudo－stochastic orbitmodelingtechniques for low earth orbiters［J］．J．Geod．，2006，80(1):47–60．

［5］ 赵春梅，程鹏飞，益鹏举．基于伪随机脉冲估计的简化动力学卫星定轨方法［J］．宇航学报，2011，32(4):762－766．［Zhao Chun－mei，Cheng Peng－fei，Yi Peng－ju．Reduced－dynamics satellite orbit determination based on pseudo－stochastic pulse estimation［J］．Journal of Astronautics，2011，32(4):762－766．］

［6］Visser P，Van den Ijssel J．Aiming at a 1cm orbit for low Earth orbiters:reduced－dynamic and kinematic precise orbit determination［J］．Space Science Reviews，2003，108:27－36．

［7］Montenbruck O，Van Helleputte T，Kroes R，et al．Reduced dynamic orbit determination using GPS code and carrier measurements［J］．Aerosp．Sci．Tech．，2005，9(3):261－271．

［8］Swatschina P．Dynamic and reduced－dynamic precise orbit determination of satellites in low earth orbits［D］．Vienna:Vienna University of Technology，2009．

［9］Colombo O L．The dynamics of global positioning orbits and the determination of precise ephemerides［J］．J．Geophys．Res:Solid Earth(1978－2012)．1989，94(B7):9167－9182．

［10］ 朱骏，王家松，陈建荣，等．HY－2卫星DORIS厘米级精密定轨［J］．宇航学报，2013，34(2):163－169．［Zhu Jun，Wang Jia－song，Chen Jian－rong，et al．Centimeter precise orbit determination for HY－2 via DORIS［J］．Journal of Astronautics，2013，34(2):163－169．］

［11］ 王文彬，刘荣芳．基于双频GPS观测的简化动力学最小二乘批处理精密定轨［J］．空间科学学报，2014，34(4):460－467．［Wang Wen－bin，Liu Rong－fang．Precise orbit determination based on reduced dynamic batch LSQ estimation method using dual－frequency GPS observations［J］．Chin．J．Space Sci．，2014，34(4):460－467．］

［12］Montenbruck O，Gill E．Satellite orbits:models，methods and applications［M］．Heidelberg:Springer Verlag，2000．

［13］ 王高雄，周之铭，等．常微分方程(第二版)［M］．北京:高等教育出版社，1982:185－196．

［14］NASA Jet Propulsion Laboratory PO．DAAC．GRACE Level 1B products［OL］．［2013－11－21］．ftp://podaac．jpl．nasa．gov/allData/grace/．

［15］Center for Orbit Determination in Europe(CODE)．High rate clocks and orbits［OL］．［2014－01－08］．ftp://ftp．unibe．ch/aiub/CODE．