电动帆航天器谷神星探测任务轨迹优化

霍明英，彭福军，赵 钧，谢少彪，3，齐乃明

(1．哈尔滨工业大学航天学院，哈尔滨150006;2．上海宇航系统工程研究所，上海201108;3．上海航天技术研究院，上海201109)

0 引言

谷神星(Ceres)是太阳系内的一颗矮行星，同时也是位于小行星带内最大的天体。目前，谷神星被很多学者认为是尚存的原行星(萌芽期的行星)之一，于45．7亿年前在小行星带中形成［1］。虽然太阳系内大多数的原行星不是和其他的原行星合并成为类地行星，就是被木星弹射到太阳系外，但是谷神星被认为是留存下来较为完整的一颗原行星［2］。因此，对谷神星的探测将非常有助于了解太阳系的起源。不仅如此，欧洲航天局已于2014年1月确认谷神星上有水蒸气冒出。谷神星的红外线光谱也显示水合矿物非常广泛的存在于谷神星上，这都证明在其内部可能存在着大量的水。甚至有天体生物学方面的科学家认为谷神星有可能是潜在的宜居性星球，因为其表面存在着生命需要的三个基本条件:液态水、能量来源和某些化学成分［3］。因此，对谷神星的探测不仅能够对太阳系形成理论提供佐证，也可以对其地表是否存在水甚至是原始生命一探究竟。鉴于谷神星探测具有很大的科学意义和现实意义，美国航空航天局(NASA)于2007年9月发射了“黎明”号太空飞船，于2011年7月抵达灶神星(Vesta)，2015年3月抵达谷神星［4］。为了将来能更快更廉价地对谷神星进行探测甚至取样返回，本文提出将电动太阳风帆(简称电动帆)推进技术应用于谷神星的探测任务中。

电动帆是由芬兰航天专家Janhunen于2004年在磁帆［5］的基础上提出的一种新兴的无推进剂消耗的推进方式［6］。与更为人熟知的太阳帆相同，电动帆可以在不消耗任何推进剂的情况下产生连续的推力，因此非常适用于长期的空间探测任务;与太阳帆不同的是，电动帆的动力来源为太阳风中带电粒子的动能冲力，而不是太阳光压。电动帆原理示意图如图1所示，电动帆由许多根长而细的金属链所组成，这些金属链通过航天器自旋进行初始展开和形状保持。航天器上的太阳能电子枪通过向外喷射电子使金属链始终保持在高度的正电位。这些带电金属链会排斥太阳风中的正电粒子，从而最终利用太阳风的动能冲力为航天器产生连续的推力，并使航天器在飞行过程中不消耗任何推进剂。Janhunen对电动帆的推进效率与目前常规推进技术进行了对比分析。分析结果表明由于电动帆在工作过程中不损耗任何推进剂，因此能够为飞行器提供持续不断的推力，工作寿命很长。通过理论计算表明，在为期10年的任务中，同样质量的电动帆所能产生的速度增量是同样质量化学火箭发动机所能产生增量的1000倍左右，同样质量电火箭发动机(SEP)所能产生增量的100倍左右［7］。同太阳帆对比方面，由于太阳帆产生的推力与相对太阳距离平方成反比关系，而电动帆产生的推力与相对太阳距离一次方成反比［8］。因此，在星际远航任务中，电动帆的推力衰减速度相对于太阳帆的推力衰减速度较慢。而且由于电动帆利用正电场对太阳风质子流进行反射，减少了反射材料质量。在同等特征加速度要求下，电动帆比太阳帆质量更轻;在同等载荷比例的情况下，电动帆产生的加速度更大。

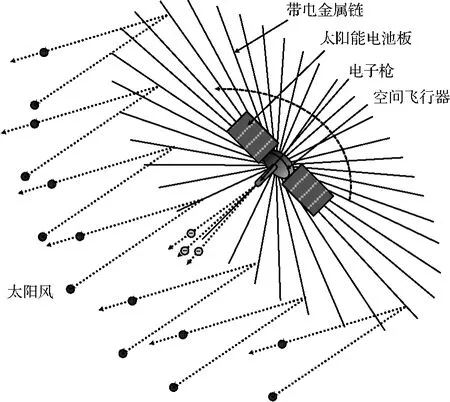
图1 电动帆原理示意图Fig．1 Conceptual sketch of an electric sail

鉴于电动帆在深空探测中的巨大潜力，欧盟于2010年12月组织召开了电动帆项目(项目编号:ESAIL EU FP7)启动会议，资助“电动帆推进技术研究项目”170万欧元资金。在“欧洲第七框架计划”的资助下，欧洲各国相关学者对电动帆开展了一系列理论及实验研究。Mengali和Quarta基于火星探测任务为背景采用间接优化算法对电动帆和太阳帆的运动轨迹进行了优化，并对比了电动帆与太阳帆的性能。通过对比可以看出，太阳帆产生的推力与相对太阳距离平方成反比关系，而电动帆产生的推力与相对太阳距离7/6次方成反比(Janhunen已通过实验更正为电动帆产生的推力与相对太阳距离一次方成反比［8］)。因此，在星际远航任务中，电动帆的推力衰减速度相对于太阳帆的推力衰减速度较慢［9］。他们还将电动帆应用于太阳系外探测任务，并通过间接优化算法对不同特征加速度电动帆的太阳系外探测轨迹进行了优化设计。轨迹优化结果表明，一个中等性能的电动帆完成太阳系外探测所用的时间为15年［10］，是旅行者1号的1/3左右。他们基于间接优化方法还对电动帆的各种空间飞行任务进行了轨迹优化，结果均表明电动帆在深空探测领域方面有很大的潜力［11－13］。

本文作者在前期的研究工作中，采用高斯伪谱法对电动帆自地球至火星的二维轨迹优化问题进行了研究［14］。在研究中忽略了火星轨道面与地球轨道面之间的倾角以及星历约束，将实际的三维轨迹优化问题简化为二维轨迹优化问题。由于谷神星公转轨道的轨道倾角较大(10．585°)，所以这种简化假设将不适用于谷神星探测任务分析中。本文在考虑星历约束的情况下，对电动帆自地球至谷神星的三维轨迹优化问题开展研究。并提出一种基于高斯伪谱法和遗传算法的混合优化算法，这种优化算法采用遗传算法生成高斯伪谱法中所需的状态变量及控制变量初值，既避免了单纯高斯伪谱法初值猜测繁琐的问题，也克服了Mengali和Quarta所采用的间接优化算法对协态变量初值敏感的问题。基于此优化算法，在不同特征推力加速度和发射时间的情况下，对电动帆航天器自地球至谷神星的过渡轨迹进行了优化，并分析了上述因素对飞行任务的影响。

1 转移轨迹优化问题描述

由于太阳风粒子流在行星引力球内受到行星磁场的影响而变得较为复杂，所以本文中电动帆轨迹优化问题主要集中于以太阳为引力中心的二体问题。为了提高数值计算效率，引入参考距离和参考时间对整个轨迹优化问题进行无量纲化处理。参考距离为一个天文单位(1au)，参考时间为地球相对太阳的公转周期。

图2 参考坐标系及推进加速度特征角Fig．2 Reference frames and propulsive acceleration's characteristic angles

1．1优化性能指标

传统航天器轨迹优化问题的性能指标大致可以分成三种，即燃料最优、时间最优和时间燃料混合最优。由于电动帆航天器在飞行过程中利用太阳风中带电粒子的动能产生推力而不消耗任何推进剂，因此电动帆航天器轨迹优化问题中的优化性能指标通常选为时间最优［9－10］，优化性能指标如下:

其中，t0为任务初始时刻，tf为任务终端时刻。在电动帆轨迹优化问题中，终端时刻tf通常为一个未知变量，而初始时刻t0可以是一个已知变量，也可以当做一个未知变量来处理。当初始时刻t0为未知变量时，轨迹优化问题不仅要得出最优的过渡轨迹，还要得出使性能指标最优的任务开始时间。

1．2动力学微分约束

在描述电动帆动力学方程时主要涉及到两个参考系，即日心黄道参考系T⊙(x，y，z)和轨道参考系TO(xo，yo，zo)。如图2所示，日心黄道参考系的原点为太阳中心，正x轴指向历元J2000．0时刻平春分点方向，正z轴垂直于J2000．0时刻黄道面并指向黄道北极方向，y轴与x轴和z轴构成右手系。轨道参考系的原点位于电动帆航天器质心，正zo轴为太阳－电动帆航天器的矢量方向，yo轴与zo轴和日心黄道参考系中的z轴垂直，方向指向飞行运动方向，xo轴与yo轴和zo轴构成右手系。电动帆航天器在日心黄道参考系下的动力学方程为:

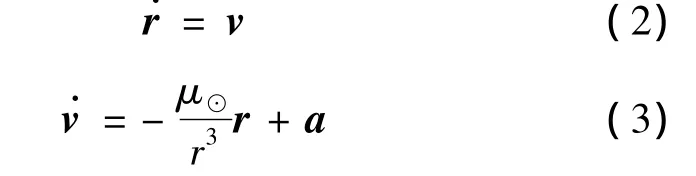
式中:μ⊙为太阳的引力常数;r=［rx，ry，rz］T为航天器在日心黄道参考系下描述的位置矢量;r=r为航天器与太阳的相对距离;v=［vx，vy，vz］T为航天器在日心黄道参考系下描述的速度矢量;a为电动帆的推进加速度矢量。

电动帆的推力是由太阳风粒子的速度、密度以及带电金属链的电压、长度和根数所决定。当电动帆远离(接近)太阳时，所能利用的太阳风粒子速度和密度将减小(增大)，Janhunen通过理论推导及实验发现电动帆产生的推力与相对太阳距离一次方成反比［8］。另外，当电动帆金属链长度和根数一定时，电动帆可以通过太阳能电子枪向外喷射电子调整金属链的电压，进而实现对推力的调整。参考Janhunen通过实验获得的电动帆推力模型［8，15］以及图2，电动帆推力加速度矢量在日心黄道参考系下可以写作:

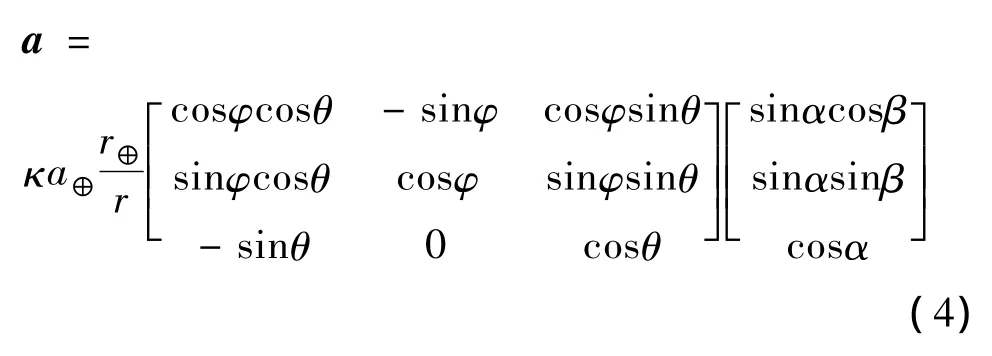
式中:a⊕为电动帆的特征加速度，即电动帆距离太阳r⊕=1au处所能产生的最大加速度值;κ∈［0，1］为电动帆推力开关系数，可以通过电子枪调整金属链的电压来调整电动帆整体的推力，这一特性与太阳帆有很大的不同;当κ=0时，电子枪处于关闭状态，电动帆无推力输出;当κ=1时，电动帆以最大特征加速度进行工作;α∈［0，αmax］为推进锥角，即电动帆推进加速度矢量与zo轴之间的夹角，Janhunen通过实验表明，电动帆航天器的推进锥角不能超过一个安全稳定阈值αmax，否则会造成电动帆航天器构型的不稳定;β∈［－π，π］为推进钟角，即电动帆推进加速度矢量在xoyo平面投影分量与xo轴之间的夹角，逆时针为正;θ∈［0，π］和φ∈［－π，π］为电动帆的极角和方位角，与电动帆位置矢量在日心黄道系下坐标［r］T⊙≜［rx，ry，rz］T的关系为

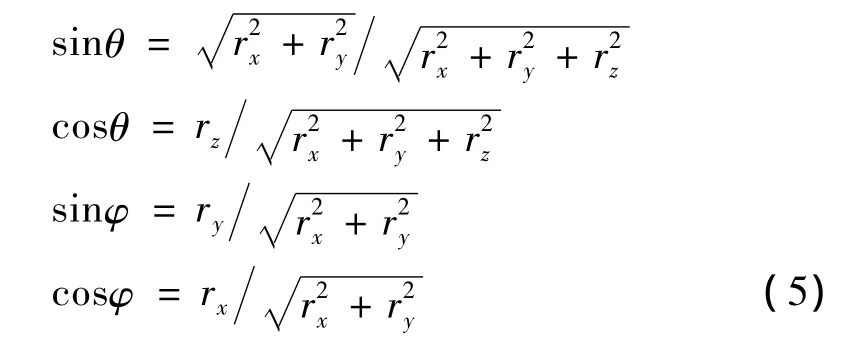
将式(3)和式(4)代入式(1)和式(2)，便可获得电动帆航天器的动力学方程:

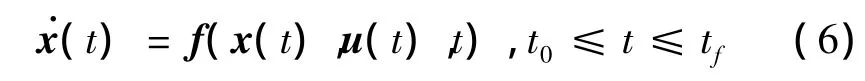
式中:状态变量为电动帆的位置及速度，即x≜［rx，ry，rz，vx，vy，vz］T;控制变量为影响电动帆推进加速度矢量的两个推进角α，β和推力开关系数κ，即u≜［α，β，κ］T;状态微分函数f(x(t)，u(t)，t)简记为［f1，f2，f3，f4，f5，f6］T。

1．3边界约束

电动帆航天器轨迹优化问题中的边界条件约束主要包括初始状态约束和终端状态约束。假设电动帆航天器在初始时刻位于地球逃逸抛物线轨迹上，且逃逸剩余能量为零，初始状态约束可写作:

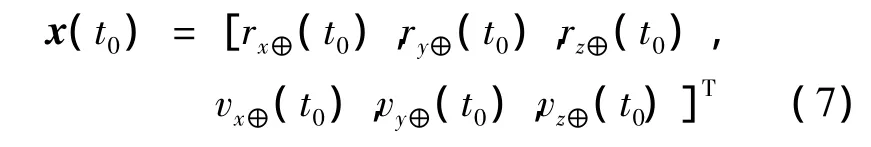
其中rx⊕(t0)，ry⊕(t0)，rz⊕(t0)和vx⊕(t0)，vy⊕(t0)，vz⊕(t0)为地球t0时刻在日心黄道参考系下的位置和速度，可通过美国喷气推进实验室(JPL)发布的DE405星历计算得出［16］。

为了完成电动帆自地球至谷神星的过渡，须在终点时刻tf时的状态变量与谷神星状态变量一致，所以终端约束条件可写作:

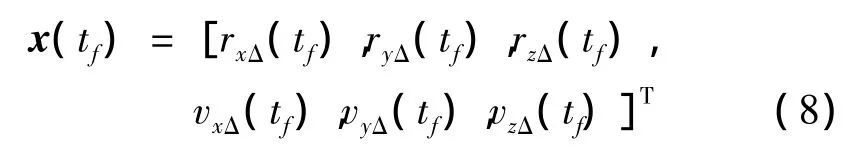
式 中:rxΔ(tf)，ryΔ(tf)，rzΔ(tf)和vxΔ(tf)，vyΔ(tf)，vzΔ(tf)为谷神星tf时刻在日心黄道参考系下的位置和速度，可通过谷神星的轨道根数计算得出。

1．4路径约束

由于航天器距离太阳越近，电动帆带电金属链所接触到太阳风高能粒子的温度、速度和密度都会变得越大，电动帆的使用寿命会越短，所以为了保证电动帆中的金属链能够长期稳定地工作，要求电动帆在飞行过程中相对太阳的距离应大于电动帆航天器允许的最小距离rmin。若电动帆金属链材质为铝合金，一般假设rmin=0．5au。综上所述，电动帆航天器在飞行过程中的路径约束可写作:

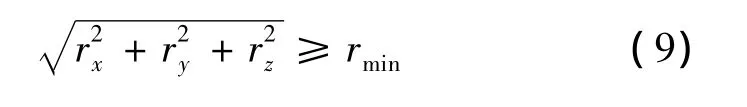
2 基于高斯伪谱法和遗传算法的轨迹优化策略

针对单纯高斯伪谱法［17］初值赋值繁琐的问题，本文提出一种结合高斯伪谱法和遗传算法的混合优化方法。混合优化算法的优化策略如下:首先以较少离散点进行高斯伪谱法离散化，并通过罚函数将有约束优化问题转化成无约束优化问题，应用遗传算法对此优化问题进行全局寻优，并对遗传算法获得的结果进行三次样条插值;然后以较多离散点进行高斯伪谱法离散化，并以可行解插值结果作为最优解计算的初值，最后采用序列二次规划算法在此初值基础上计算得出最优解，基于混合优化算法的电动帆轨迹优化流程图如图3所示。

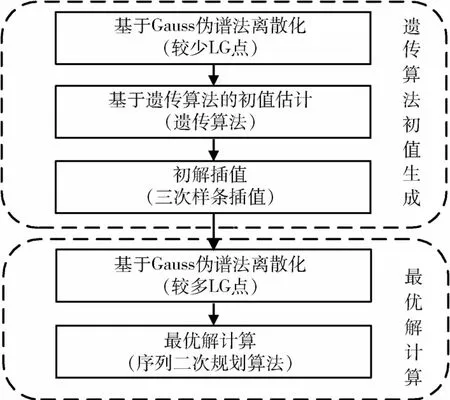
图3 混合优化算法计算流程Fig．3 The flow chart of the hybrid optimization method

2．1基于高斯伪谱法离散化

最优控制问题的时间区间为［t0，tf］，而高斯伪谱法的离散点分布在区间［－1，1］之间［18］。所以需要通过引入一个新的时间变量τ，将上述定义在［t0，tf］区间上的最优控制问题转化成定义在［－1，1］区间内，时间变换关系为:

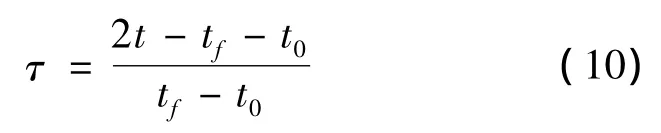
由于电动帆航天器轨迹优化问题中的性能指标函数不包含积分项，所以在离散化后的非线性规划问题中仍可以写成非常简单的形式:

为了将原无限维的连续非线性最优控制问题转化成有限维的非线性规划问题，需要用N阶Lagrange插值多项式对原问题中连续的状态变量和控制变量进行插值:

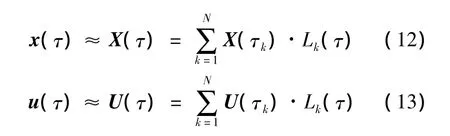
式中:X(τ)和U(τ)分别为状态变量和控制变量的N阶近似多项式;Lk(τ)，k=1，2，…，N，为N阶Lagrange插值多项式:

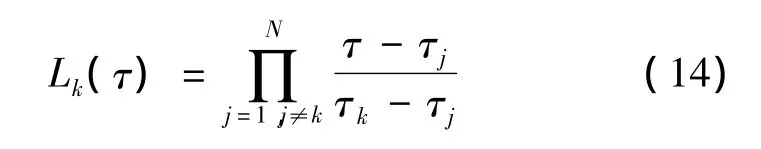
式中:τk，k=1，2，…，N为N个Legendre-Gauss(LG)点，状态变量和控制变量是在这些非均匀分布的LG点上进行离散化的。这N个LG点是N次Legendre多项式的零点，N次Legendre多项式的表达式如下:

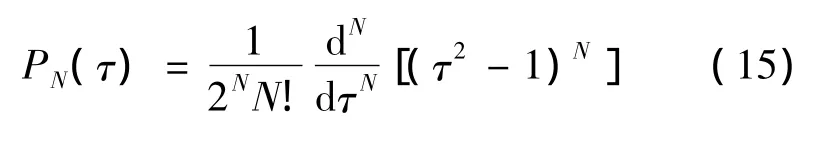
但是这些离散点未包括初始时刻及终端时刻所对应的点，所以定义τ0=－1和τN+1=1分别对应初始时刻和终端时刻。为了表达的方便，简记状态变量在离散点 τi，i=0，．．．，N+1上的值X(τi)为Xi，控制变量在离散点 τi，i=0，…，N+1上的值U(τi)为Ui，时间在离散点 τi，i=0，…，N+1上的值t(τi)为ti。

为了将连续的非线性最优控制问题转化成非线性规划问题，需要把状态变量的微分约束转化成等式约束。对式(11)求导可得:

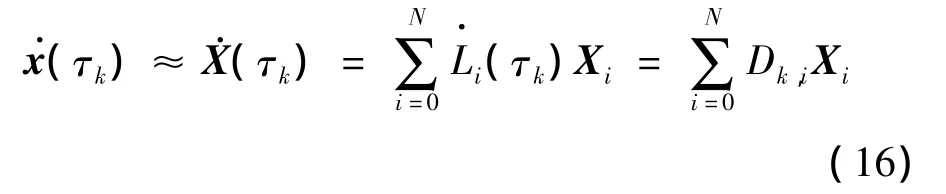
式中:Dk，i，i=0，1，…，N，k=1，2，…，N是状态微分矩阵D中的一个元素，可通过下式进行计算:

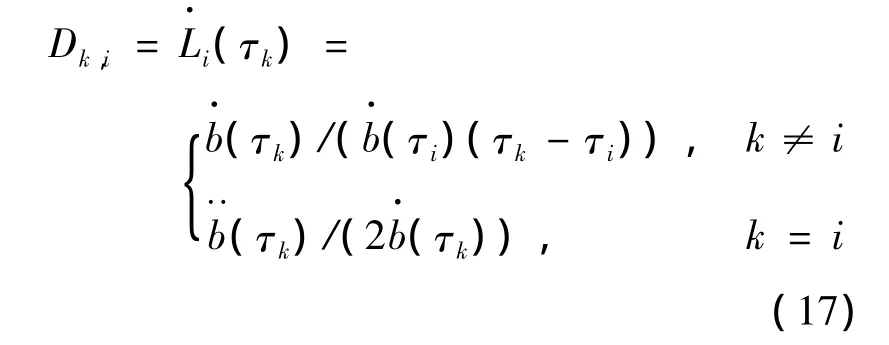
至此，便可将式(5)中描述的6个状态变量微分约束转化成下面所示的6N代数等式约束:

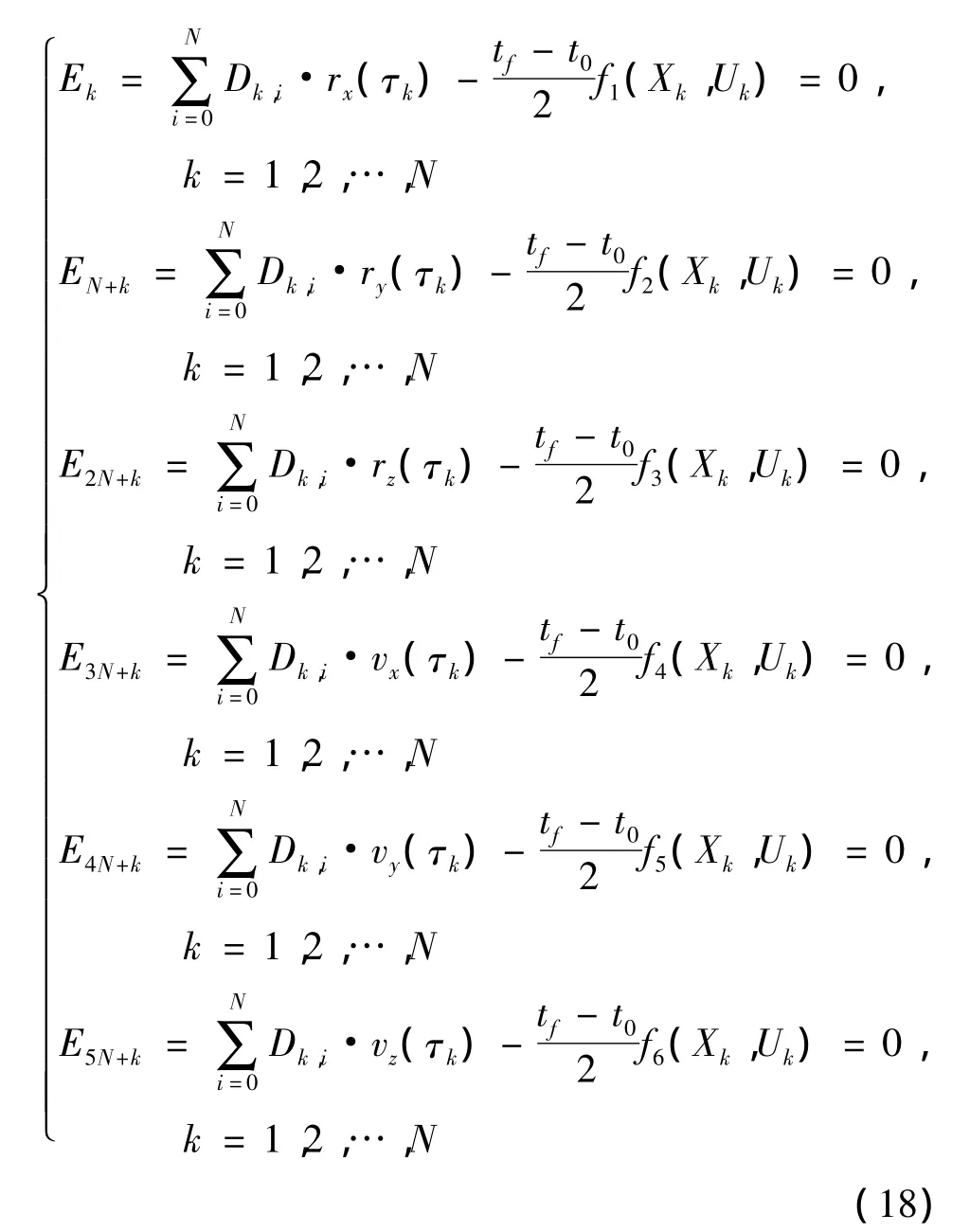
通过高斯积分可获得电动帆航天器在终点时刻tf的状态，进而将式(7)描述的边界条件约束转化为6个等式约束:

式中:wk，k=1，2，…，N，为高斯积分中的积分权重。

将路径约束式(8)在LG点上进行离散化，便可得到离散化的路径约束:

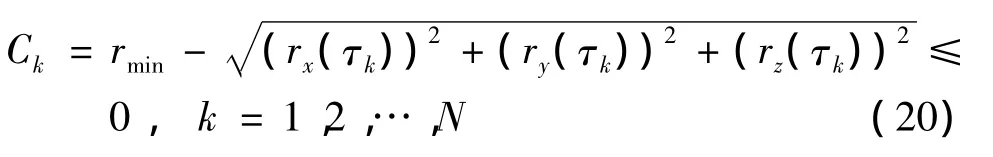
综合式(10)和式(17)～(19)，便可将式(5)～(8)描述的连续最优控制问题转化成下述的非线性规划问题:

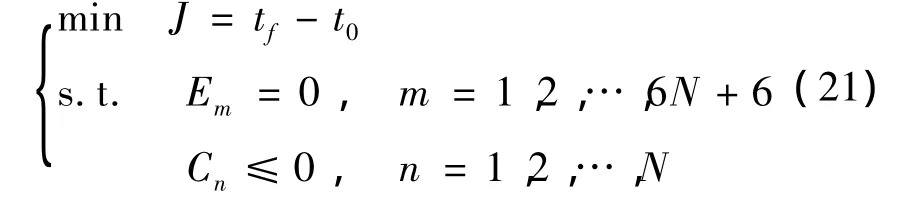
对于初始时间t0不固定的电动帆航天器轨迹优化问题，通过高斯伪谱法离散化所得到的非线性规划问题中共有9N+2个设计变量，分别是6N个状态变量，3N个控制变量，以及初始时间t0和终端时间tf。等式约束个数为6N+6个，不等式约束个数为N个。

2．2基于遗传算法的初值生成

对于式(20)所描述的非线性规划问题，序列二次规划算法是最常用的参数化寻优方法，但是在实际应用中却存在一定困难。当选取LG点个数N较多时，设计变量数目会比较庞大，为序列二次规划算法给定设计变量初值会十分繁琐，且在无先验知识情况下有一定难度。假设LG点个数N=60，根据上一节讨论的内容可知设计变量个数为542。对于如此多的设计变量，在序列二次规划算法应用中给定设计变量初值的工作会比较繁琐，且不恰当的初值会使问题收敛到不可行解。不仅如此，序列二次规划算法不具备全局寻优的能力，所得到的解主要决定于所猜测的设计变量初值，所以多是靠近初值最近的局部最优解。

因此，本文提出采用遗传算法全局寻优获得高斯伪谱法中非线性规划问题状态变量及控制变量的初值。通常来说遗传算法只能用于处理无约束的参数优化问题，然而本节中的非线性规划问题是有等式约束及不等式约束的。因此，优化问题的目标函数将不只包括时间最优问题，也应该通过增加罚函数将等式约束考虑在内。基于遗传算法优化问题的性能指标函数(适应度函数)可写成:

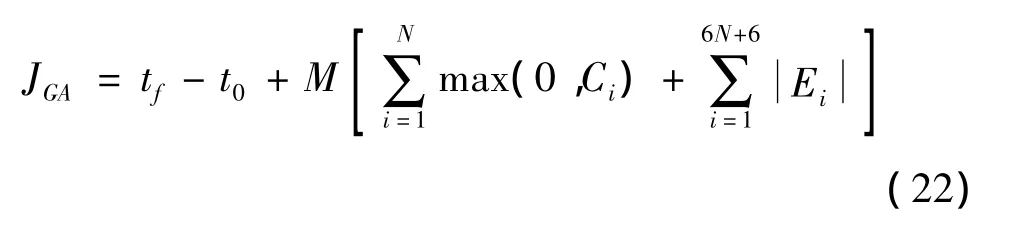
式中:M为惩罚系数。

2．3基于序列二次规划的最优解计算

序列二次规划算法是目前应用最广泛且适用性最好的一种基于梯度的非线性规划问题求解方法。序列二次规划法的优点是计算效率高、收敛速度快且所得解精度较高，缺点是需要提供初值猜测，且所得的解对设计变量初值猜测具有一定依赖性，非常容易得到局部最优解。因此，本文通过遗传算法在无任何初值猜测的情况下通过全局搜索生成较少LG离散点的初解，然后通过插值得到序列二次规划算法所需的初值猜测。这样就实现了在无任何初始输入的情况下，完成对电动帆航天器轨迹优化问题最优解的求解。避免了在无先验知识的情况下，对初值进行猜测十分繁琐且困难的情况。而且由于所使用的设计变量初值是通过全局搜索而生成的，所以所获得的解更接近于全局最优解。本文中序列二次规划算法所要处理的非线性规划问题如式(15)所示，这类非线性规划问题可通过非线性规划求解器SNOPT［19－20］进行求解。

3 计算结果分析

3．1仿真算例

本节在电动帆航天器自地球至谷神星转移轨迹优化中，假设电动帆航天器在初始时刻位于地球逃逸抛物线轨迹上，且逃逸剩余能量C3=0 km2/s2。谷神星的位置和速度通过轨道根数(如表1所示)计算得出，计算中忽略了谷神星轨道的章动影响。电动帆航天器的特征加速度为a⊕=1 mm/s2，最大推进锥角αmax=35°，最小允许相对太阳距离rmin=0．5au。飞行初始时刻的选择范围为2020年1月1日(JD2458849．5)到2030年12月31日(JD2462866．5)。在基于遗传算法的初值计算中，LG离散点个数为10，种群大小为200，迭代次数为50，惩罚系数为100。在基于序列二次规划算法的最优解计算中，LG离散点个数为60，约束允许误差为10－7。

基于上述参数对电动帆航天器自地球－谷神星飞行轨迹进行了优化，数学仿真运行的环境为MATLAB(R2010a)，运行平台为双核2．7GHz主频的个人计算机，初值生成所用时间为22分45秒，得出最优解所用时间为14分22秒。由于所采用的轨迹优化方法利用遗传算法进行初值生成，其优化计算效率比单纯的高斯伪谱法略低，但是对于离线轨迹优化来说仍在可接收的范围之内。电动帆航天器自地球－火星飞行轨迹如图4所示，若电动帆航天器于2030年8月3日离开地球影响球，将历时879天于2032年12月29日抵达谷神星引力影响范围。由电动帆航天器自地球至谷神星的控制变量－时间曲线(图5)可以看出，混合优化算法得出的控制变量能够满足控制变量约束，且变化相对平缓，利于工程实现。

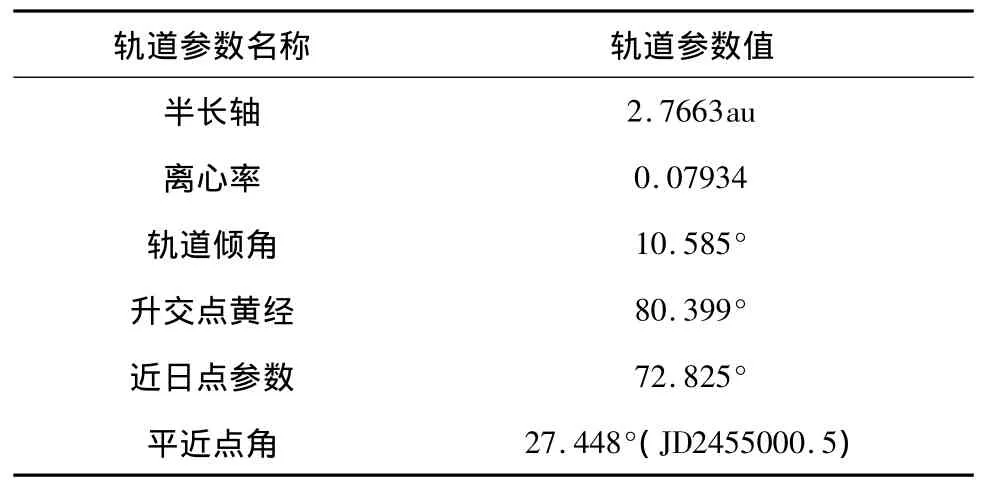
表1 谷神星轨道参数Table 1 Orbital parameters of Ceres

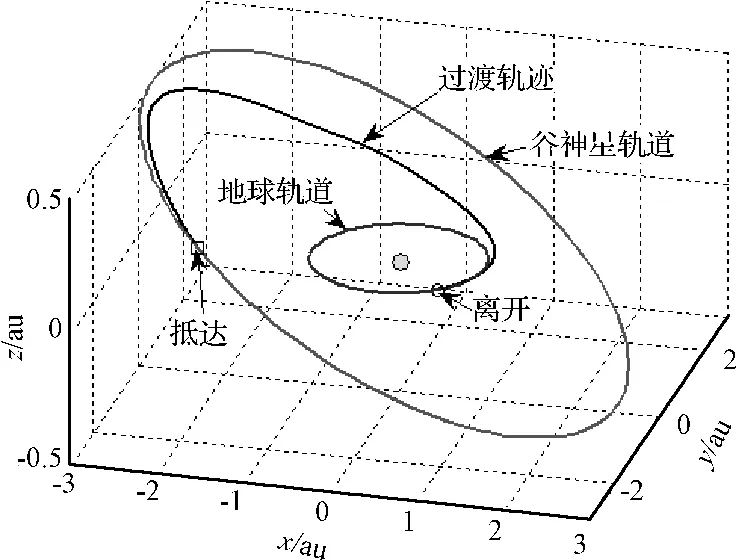
图4 地球－谷神星过渡轨迹(a⊕=1 mm/s2)Fig．4 Earth－Ceres optimal transfer trajectory(a⊕=1 mm/s2)

为了验证轨迹优化算法的精度，将所得到的控制变量插值后代入到控制模型中进行积分。积分公式为四阶－五阶龙哥库塔积分公式，积分函数为ode45，积分相对精度为10－9，积分得出的状态变量结果绘制于图6和图7。由这两个图可以看出，混合优化算法得到的轨迹与相同控制变量积分得到的轨迹差别较小(在图6和图7中两条轨迹都已画出，积分轨迹为实线，优化得出的原轨迹为虚线，但是两者在图中过于接近已经基本重合)。这是由于高斯伪谱法所采用的高斯积分公式具有较高的精度，这也正是高斯伪谱法近年来得到相关学者重视的一个原因。通过积分结果对交会处的相对位置和相对速度进行分析，位置终端误差为35616 km，小于谷神星的引力球半径(约为47000 km);速度终端误差为23．526 m/s，相对谷神星的逃逸能量小于零，能够实现与谷神星的交会。在真实的任务轨迹优化中，可通过增加高斯伪谱法的LG点个数来进一步提高交会精度。

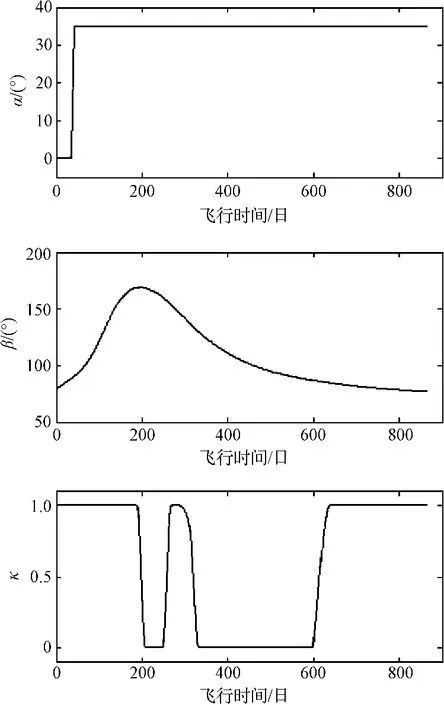
图5 控制变量－时间曲线(a⊕=1 mm/s2)Fig．5 Time histories of the control variables(a⊕=1 mm/s2)

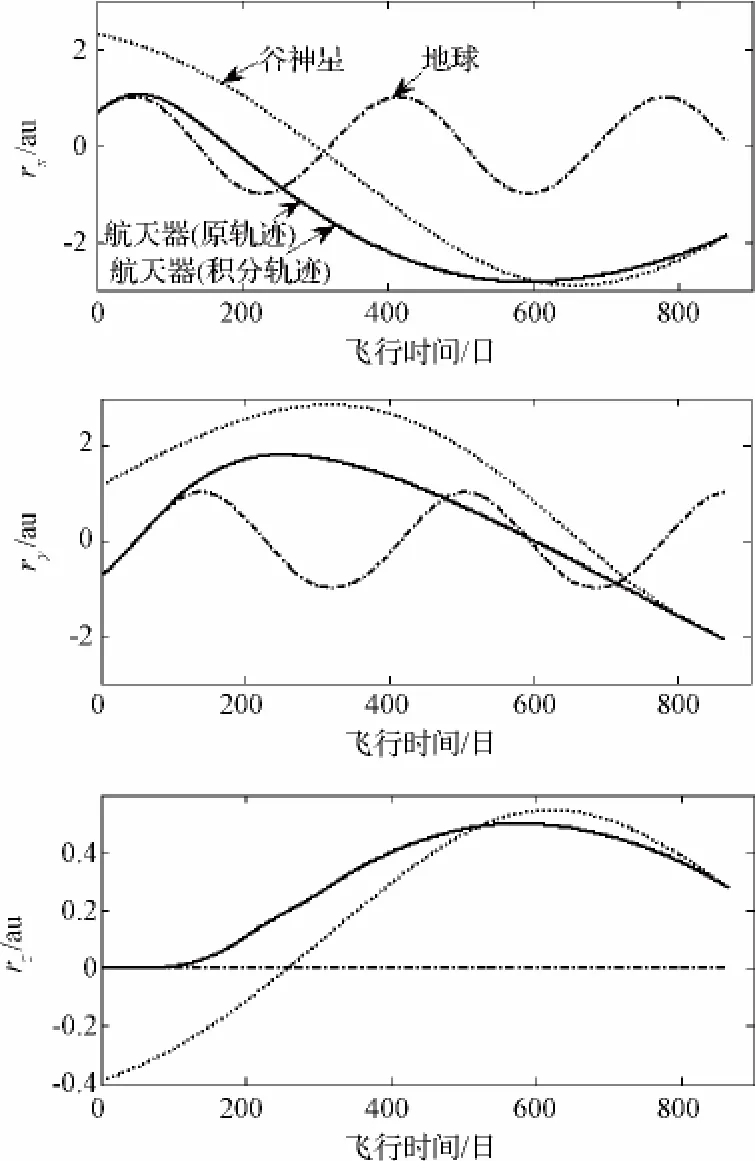
图6 位置矢量－时间曲线(a⊕=1 mm/s2)Fig．6 Time histories of the position vector(a⊕=1 mm/s2)

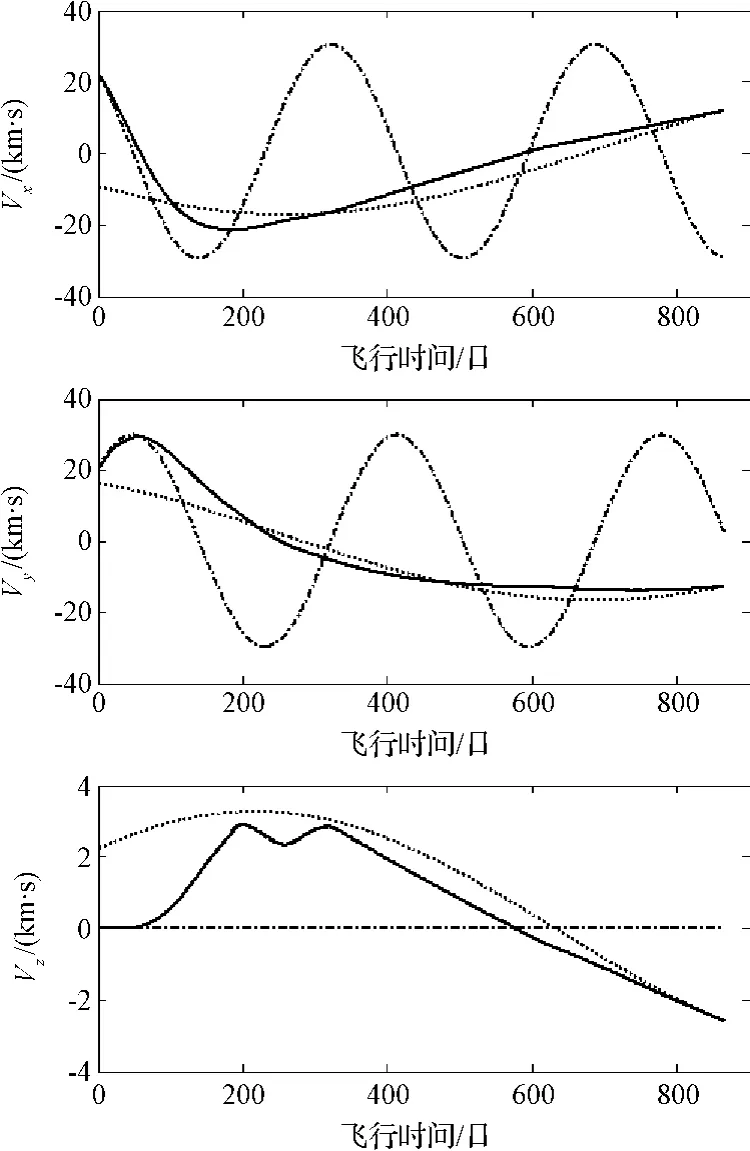
图7 速度矢量－时间曲线(a⊕=1 mm/s2)Fig．7 Time histories of the velocity vector(a⊕=1 mm/s2)

3．2起始时间对探测任务的影响

为了进一步验证混合优化算法的有效性以及考察起始时间t0对探测任务的影响，本节对不同起始时间情况下电动帆航天器自地球至谷神星的飞行轨迹进行优化。本节中起始时间t0不作为设计变量，而是自2020年1月1日(JD2458849．5)到2030年12月31日(JD2462866．5)每30天为两个仿真的时间间隔进行指定起始时间的轨迹优化，共计134个轨迹优化算例，其余仿真参数均与上一节一致，飞行时间(tf－t0)总结在图8中。

由图8可以看出，电动帆航天器自地球至谷神星的飞行时间随着起始时间的变化呈周期性波动，在3720天内共波动8次，平均变化周期为465天，这一数值与谷神星和地球的会合周期466．7天十分接近。出现这种现象的原因是当电动帆航天器从地球轨道到达谷神星轨道时，谷神星也必须同时达到，才能使航天器与谷神星实现交会。所以航天器发射时地球与谷神星的相对位置将直接影响飞行所需时间，而两者相对位置近似成周期性变化，变化周期既是谷神星和地球的会合周期。这就是电动帆航天器自地球至谷神星飞行时间变化周期与交会周期相近的原因。另外，由于谷神星轨道倾角及偏心率等因素的影响，相邻波动段内的飞行时间并不完全相等，而是存在一定差异。

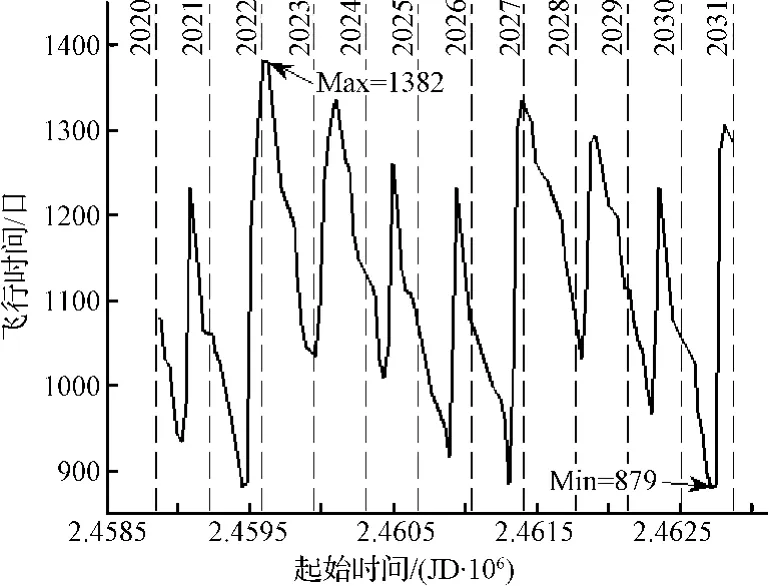
图8 不同起始时间情况下的最小飞行时间(a⊕=1 mm/s2)Fig．8 Minimum transfer time as a function of the starting date(a⊕=1 mm/s2)

3．3特征加速度对探测任务的影响

为了考察电动帆航天器特征加速度a⊕对所需飞行时间的影响，以不同特征加速度下电动帆自地球至谷神星的过渡轨迹进行了优化计算。考虑的特征加速度范围为0．4 mm/s2～2 mm/s2，每个仿真之间的特征加速度间隔为0．1 mm/s2，其余仿真参数与第3．1节中一致。不同电动帆特征加速度下地球－谷神星过渡时间如图9所示，电动帆航天器的特征加速度越小，完成过渡所需要的飞行时间越长。当特征加速度小于0．6 mm/s2时，飞行时间有显著的增加。通过对轨迹的分析可知，航天器在自地球至谷神星的过渡过程中可粗略的划分成两个调整任务，即轨道半长轴的增大和轨道倾角的调整。电动帆特征加速度的大小对轨道半长轴调整所用时间影响较大，而对轨道倾角调整时间影响相对较小。当电动帆加速度大于0．6 mm/s2时，轨道半长轴调整任务先完成，影响任务完成时间的主要限制为轨道倾角的调整，所以过渡所用时间变化相对平缓。当电动帆加速度小于0．6 mm/s2时，轨道倾角调整任务先完成，影响任务完成时间的主要限制为轨道半长轴的增长，所以过渡所用时间变化相对较大。

考虑一个依据现有技术比较合理的电动帆特征加速度a⊕=0．6 mm/s2，电动帆航天器将历时1014天完成自地球至谷神星的过渡，比采用电推进技术的黎明号空间探测器(历时1388天完成自地球至灶神星的过渡，之后又历时约920天完成自灶神星至谷神星的过渡)所用时间较短。不仅如此，由于电动帆在飞行过程中不消耗任何推进剂，所以在完成上述任务后仍可继续进行其他飞行任务，如取样返回和其他天体探测，甚至太阳系边界探测等，减少飞行任务成本。

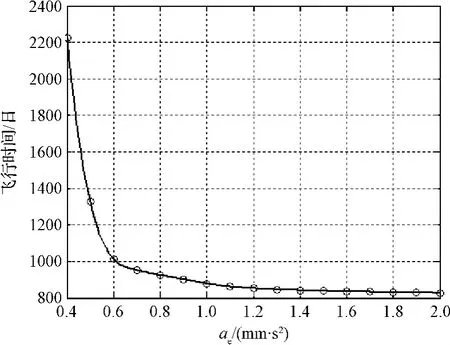
图9 不同特征加速度情况下的最小飞行时间Fig．9 Minimum transfer time as a function of the characteristic acceleration

通过以上的轨迹优化算例可知，所提出的混合优化算法是有效的，能够在无任何初值猜测的情况下完成电动帆航天器飞行轨迹的优化。另外，一个具有中等特征加速度的电动帆航天器便能在可接受的时间内完成自地球至谷神星的过渡，所以电动帆航天器是适用于谷神星探测任务的。

4 结论

为了将来能更快更廉价地对谷神星进行探测，提出将电动帆推进技术应用于谷神星探测任务中。并提出一种结合高斯伪谱法和遗传算法的混合优化算法对电动帆自地球至谷神星的轨迹进行了优化。数学仿真结果表明:1)电动帆航天器自地球至谷神星的飞行时间随着起始时间的变化成周期性波动，波动周期基本与地球－谷神星会合周期基本一致;2)电动帆航天器的特征加速度越小，完成过渡所需要的飞行时间越长，且一个具有中等特征加速度的电动帆航天器便能在可接受的时间内完成自地球至谷神星的过渡;3)所提出的混合优化算法是有效的，能够在无任何初值猜测的情况下完成电动帆航天器飞行轨迹的优化，避免了单纯高斯伪谱法初值赋值繁琐的问题。

［1］Petit J，Morbidelli A．The primordial excitation and clearing of the asteroid belt［J］．Icarus，2001，153(2):338–347．

［2］McCord T B，Sotin C．Ceres:evolution and current state［J］．Journal of Geophysical Research，2005，110(E5):1－14．

［3］ZOL新闻中心．太阳系第二大“蓄水池”谷神星或存在外星生命［EB/OL］．2015－01－02［2015－01－02］．http://news．zol．com．cn/article/368722．html．

［4］Rayman M D，Mase R A．Dawn's operations in cruise from Vesta to Ceres［J］．Acta Astronautica，2014，103:113－118．

［5］Zubrin M，Andrews G．Magnetic sails and interplanetary travel［J］．Journal of Spacecraft and Rockets，1991，28(2):197–203．

［6］Janhunen P．Electric sail for spacecraft propulsion［J］．Journal of Propulsion and Power，2004，20(4):763–764．

［7］Janhunen P．Status report of the electric sail in 2009［J］．Acta Astronautica，2011，68(5－6):567－571．

［8］Janhunen P．The electric solar wind sail status report［C］．European Planetary Science Congress，Rome，Italy，Sep 19－24，2010．

［9］Mengali G，Quarta A A，Janhunen P．Electric sail performance analysis［J］．Journal of Spacecraft and Rockets，2008，45(1):122－129．

［10］Quarta A A，Mengali G．Electric sail mission analysis for outer solar system exploration［J］．Journal of Guidance Control and Dynamics，2010，33(3):740－755．

［11］Quarta A A，Mengali G，Janhunen P．Optimal interplanetary rendezvous combining electric sail and high thrust propulsion system［J］．Acta Astronautica，2011，68(5－6):603－621．

［12］Mengali G，Quarta A A，Janhunen P．Considerations of electric sailcraft trajectory design［J］．Journal of British Interplanetary Society，2008，61(8):326－329．

［13］Mengali G，Quarta A A．Escape from elliptic orbit using constant radial thrust［J］．Journal of Guidance Control and Dynamics，2009，32(3):1018–1022．

［14］ 齐乃明，霍明英，袁秋帆．电动帆轨迹优化及其性能分析［J］．宇航学报，2013，34(5):634－641．［Qi Nai-ming，Huo Ming-ying，Yuan Qiu-fan．The electric sail trajectory optimization and performance analysis［J］．Journal of Astronautics，2013，34(5):634－641．］

［15］Janhunen P．Increased electric sail thrust through removal of trapped shielding electrons by orbit chaotisation due to spacecraft body［J］．Annales Geophysica，2009，27(8):3089－3100．

［16］Standish E M．JPL planetary and lunar ephemerides，DE405/LE405［EB/OL］．2008［2008］．http://iau-com m4．jpl．nasa．gov/de405iom/de405iom．pdf．

［17］David B．A Gauss pseudospectral transcription for optimal control［D］．Cambridge:Massachusetts Institute of Technology，2005．

［18］ 唐国金，罗亚中，雍恩米．航天器轨迹优化理论、方法及应用［M］．北京:科学出版社，2011:149－151．

［19］Gill P E，Murray W，Saunders M A．User’s guide for SNOPT V7:software for large-scale nonlinear programming［EB/OL］．2008［2008］．http://ccom．ucsd．edu/～peg．

［20］Gill P E，Murray W．SNOPT:an SQP algorithm for large-scale constrained optimization［J］．SIAM Journal on Optimization，2002，12(4):979–1006．