考虑跟踪制导的小天体着陆轨迹闭环优化方法

胡海静，高 艾，朱圣英，崔平远

(1．北京理工大学宇航学院，北京100081;2．深空自主导航与控制工信部重点实验室，北京100081;3．飞行器动力学与控制教育部重点实验室，北京100081)

0 引言

小天体探测作为人类了解太阳系形成与演化、生命起源与进化以及防御外来天体撞击的重要途径，是深空探测的重要内容之一。对小天体的近距离探测始于20世纪90年代，伴随着空间技术水平的快速提高，探测方式也由飞越探测向绕飞、着陆和采样返回发展。小天体着陆探测任务的开展有助于对目标星进行实地、长期考察，获得更多精确可靠的数据;同时，小天体着陆技术是小天体采样返回任务成功实施的基础，有助于将小天体的土壤和岩石带回地球进行深入研究［1－2］。

目前，人类已成功实施两次小天体着陆探测任务。2001年，美国宇航局(NASA)的近地小行星交会任务(Near Earth Asteroid Rendezvous，NEAR)成功在Eros433着陆［3］。2005年，日本宇航局(JAXA)的隼鸟号成功在Itokawa小天体着陆，并首次实现从小天体采样并返回地球［4］。另外，2014年，罗塞塔任务实现在彗星67P/Churyumov-Gerasimenko表面着陆。然而，由于锚定系统故障，着陆器Philae号与小天体表面碰撞，由于小天体引力非常弱，Philae号碰撞后发生弹跳，并最终稳定在阴影区，导致其太阳能电池板无法充电，从而处于休眠状态。其着陆与弹跳过程如图1所示，该过程显示，仅仅1 m/s的速度误差导致Philae号碰撞后两个小时处于弹跳状态，并引发无法正常启动的严重后果，表明小天体着陆精度，尤其是着陆速度误差对任务设计非常关键，需要尽可能提高小天体着陆精度。

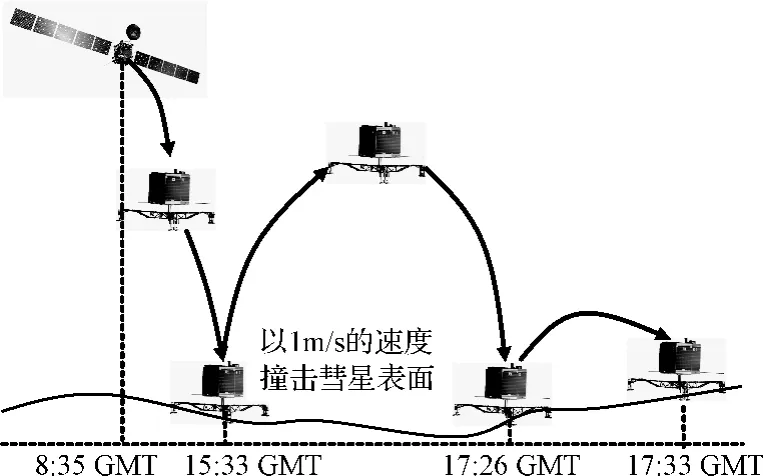
图1 Philae号附着过程示意图Fig．1 Illustration of the landing process of Philae

然而，着陆小天体动力学存在的参数不确定性(小天体自旋角速度及推力大小和方向偏差等)和探测器的初始状态偏差对着陆误差有不可忽视的影响。另外，小天体形状不规则导致小天体附近的引力场也非常不规则，导致探测器运动规律较为复杂。以上两方面因素导致在小天体表面成功实现精确着陆非常困难。Broschart等学者针对小天体着陆开环控制策略进行了研究，结果表明，在能对小天体进行精确建模以及对探测器状态进行精确估计的基础上，开环控制策略能够用于小天体着陆任务［5－6］。然而，在任务设计阶段往往无法完全确知目标天体参数及初始状态存在的偏差，实施小天体着陆开环控制策略会引起较大的着陆误差，存在较大任务风险。针对无法获得精确动力学模型问题，文献［7］给出一种利用Gauss-Markov过程的小天体着陆导航与制导算法，该方法采用一阶Gauss-Markov过程近似着陆探测器轨道动力学中的无模型加速度，利用扩展卡尔曼滤波估计探测器的位置、速度及无模型加速度。另外，文献［8］提出一种光学导航方案，利用光学相机实现特征点的提取和跟踪，并采用激光测距仪实现矢量测量，达到提高探测器状态估计精度的目标。在此基础上，学者通过设计反馈制导律能够降低跟踪误差［9－11］。然而，该过程忽略了着陆轨迹对跟踪效果的影响，跟踪不同着陆轨迹对着陆误差有一定影响。研究表明，燃料最优着陆轨迹的推力呈现bang-bang形式［12－14］。在存在参数不确定性和初始状态偏差的情况下，跟踪bang-bang推力形式的最优着陆轨迹极易引起控制系统的饱和，从而影响着陆精度的提高。

针对参数不确定性和初始状态偏差的影响，学者对航天器轨迹不确定性的非线性递推方法进行了研究［15－16］，该方法有助于分析参数不确定性随非线性动力学的变化过程，但因计算量大而难以在着陆轨迹优化中直接应用。文献［17］针对星际转移任务中初始状态偏差的影响，在轨迹优化的过程中递推了动力学模型的开环线性协方差，并作为优化问题的性能指标求解了最优轨迹，能够降低初始状态偏差的影响。文献［18－19］分别从最优控制、轨迹优化角度推导研究了如何降低参数的敏感度。

本文以小天体着陆任务为背景，首先，建立了小天体着陆动力学模型，并分析了燃料最优着陆问题。为了更好跟踪着陆轨迹，首先采用线性二次型调节器(Linear Quadratic Regulator，LQR)技术设计了反馈制导律，并在此基础上推导了对不确定参数和初始状态的闭环敏感度矩阵方程。该敏感度矩阵方程反映了闭环情况下动力学模型对参数和初始状态的敏感程度。最后，构造了包含燃料消耗和敏感度的性能指标，并采用高斯伪谱法进行了求解。该方法综合考虑了小天体着陆的燃料消耗和动力学模型对参数和状态不确定性的敏感度，因而获得的最优轨迹既能节省燃料，又能对参数和状态偏差不敏感。

1 小天体着陆动力学与最优问题描述

1．1坐标系定义与着陆动力学

定义小天体固连坐标系Σa:坐标原点oa位于小天体的质心，za轴沿小天体自旋轴方向，xa轴沿小天体最小惯量轴方向，ya轴满足右手系法则，如图2所示。

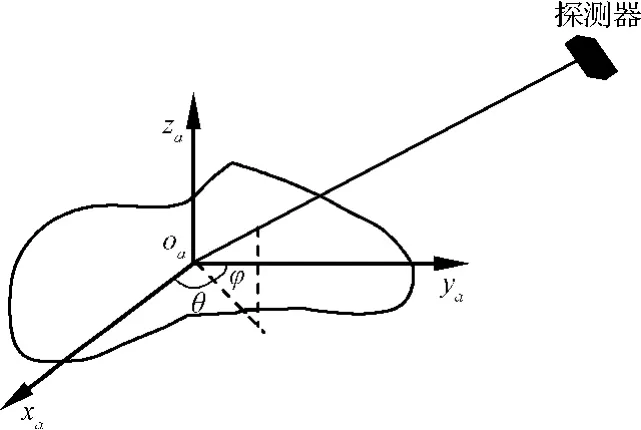
图2 小天体固连坐标系示意图Fig．2 Sketch map of the body-fixed coordinate frame

在小天体固连坐标系下，探测器着陆动力学方程可以表达为:

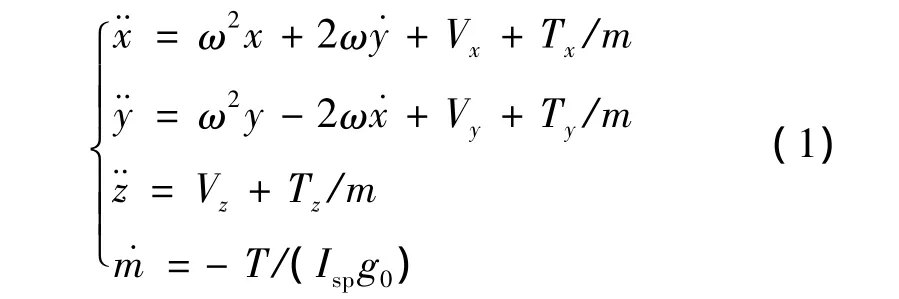
式中:x，y，z分别为探测器的三轴位置，m为探测器质量，ω为小天体的自旋角速度。Tx，Ty，Tz分别为三轴方向的控制力，其中，Tx=T cosφTcosθT，Tx=T cosφTsinθT，Tz=T sinφT，T为推力大小(Tmin≤T≤Tmax)，Tmin、Tmax分别为发动机最小和最大推力，φT和θT为推力方向角。Isp为发动机比冲，g0为地球海平面引力加速度。Vx，Vy和Vz分别为小天体引力势函数的一阶偏导数，V为小天体的引力势函数，其四阶球谐函数表达式为如下形式:

式中:μA=GM为小天体引力常数，a为小天体名义半径，θ，φ，r分别为探测器所处经度、纬度和半径。C20，C22，C40，C42和C44分别为引力势函数的系数。

为了便于表达，可以将上述动力学方程写成如下简化形式:

式中:X=［x y z˙x˙y˙z］T，T=［TxTyTz］T。

1．2小天体着陆优化问题描述

小天体软着陆是探测器从初始探测轨道上某处，经一段时间减速以速度接近零到达目标点，从而实现成功着陆。小天体着陆轨迹优化是在满足动力学约束、初始状态约束、末端状态约束以及路径约束前提下，对探测器的控制力进行优化以满足某项性能指标。其中，燃料消耗与探测任务成本直接相关，降低燃料消耗对对星际着陆任务有重要意义。

探测器的动力学约束即为式(1)。假设初始状态为初始轨道的某一点，约束可表达为:

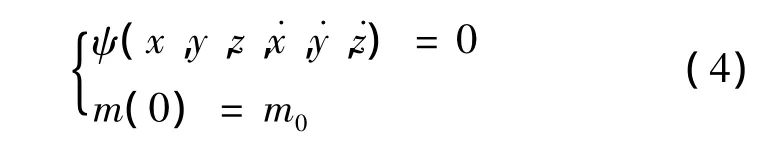
探测器终端约束为探测器终端状态约束和终端质量约束。其中，终端状态约束为探测器以接近为零的速度着陆到目标着陆点;终端质量约束为探测器的最终质量要超过其干重。

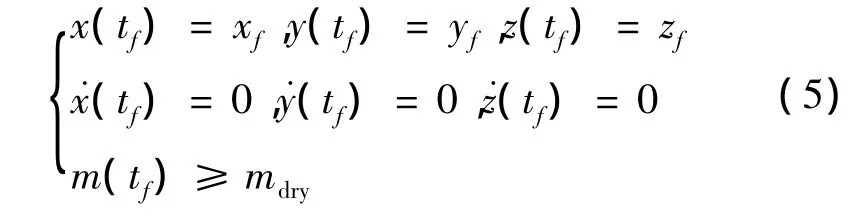
式中:tf为到达目标附着点的时刻，mdry为探测器干重，即全部燃料耗尽后的质量。

在探测器附着到小天体表面的过程中，探测器应避免与其发生碰撞，其路径通过定义如图3所示滑翔面约束能够避免与小天体发生碰撞。

在满足以上约束基础上，对如下性能指标函数进行求解能够获得燃料最优着陆轨迹:

从小天体着陆动力学方程可以看出，探测器t时刻的状态变量X(t)与其初始状态、发动机推力加速度、小天体自转角速度有关，即

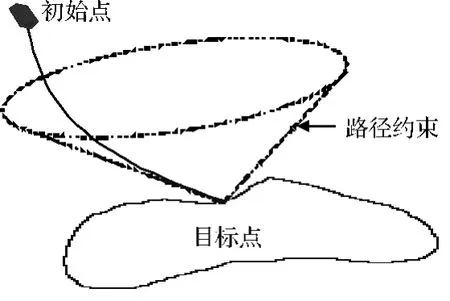
图3 小天体着陆路径约束Fig．3 Path constraint for landing on small bodies

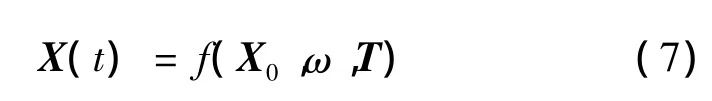
式中:X0为探测器初始状态。然而在任务设计阶段无法完全获知小天体的动力学参数，另外，探测器实施着陆任务时的初始状态及推力器的大小和方向均存在一定程度的偏差。如果忽略这些参数不确定性会对着陆误差产生一定影响，其影响的大小取决于着陆轨迹对参数的敏感度及参数误差的大小。为了提高着陆精度，需要在优化过程中通过设计闭环制导律抑制误差的影响。

2 小天体着陆闭环优化方法

采用标称模型能够较为方便的求解燃料最优轨迹，然而，动力学的参数不确定性及探测器初始状态的偏差对着陆误差有一定影响。对此，本节提出了一种考虑跟踪制导的小天体着陆闭环优化方法。首先，在设计的反馈制导律基础上推导了闭环敏感度矩阵方程，并能根据该方程求解末端状态对不确定参数的敏感度，反映了存在反馈制导律的情况下动力学对参数和初始状态偏差的敏感程度。通过在构造性能指标时加权考虑燃料消耗与敏感度，有望实现在节省燃料的同时对参数和状态偏差不敏感。

2．1反馈制导律设计

为了在优化过程中求解闭环的敏感度矩阵，首先需要设计跟踪制导律。由于优化过程需要大量调用敏感度矩阵及制导律的求解函数，为了提高效率，此处采用LQR技术设计了反馈增益。

对于LQR制导策略，性能指标取如下形式:

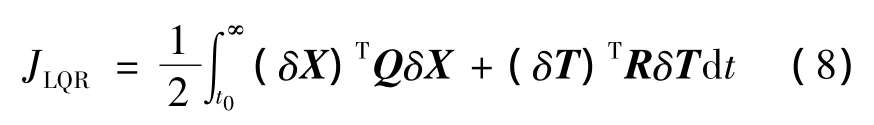
式中:δX=X－XN，δT=T－TN，下标N表示轨迹优化过程生成的标称量。Q和R分别为正定的权重矩阵，根据Bryson原则可以取如下形式:

式中:δx1max，…，δxnmax和 δT1max，…，δTnmax分别为n维状态和m维控制量的最大期望偏差。

沿标称轨迹，可以将小天体着陆动力学做线性化处理:

式中:A和B分别为动力学的雅克比矩阵。

通过设计反馈制导律δT=－KδX可以使性能指标JLQR最小，其中，反馈控制矩阵K为:

式中P可通过求解代数黎卡提方程获得:

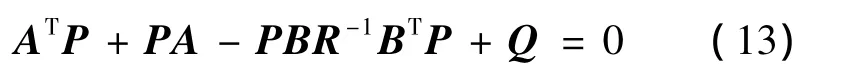
通过上述推导，反馈控制增益则可通过高效求解线性优化问题获得。

2．2燃料/敏感度加权性能指标

在小天体着陆过程中，探测器的初始状态、小天体的自旋角速度和推力的大小和方向的不确定性对着陆误差有重要影响，因而，在优化过程中需要能够降低动力学对这些参数的敏感度。

假设推力大小和方向的误差为正态分布，则可根据随机变量的性质将推力大小和方向的误差转化到三个轴方向:

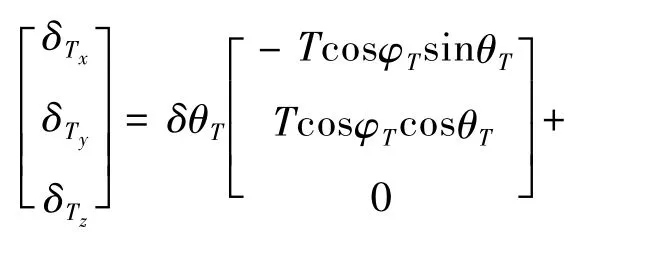
因而，小天体着陆动力学对推力偏差的敏感度向量可以表示为如下形式:

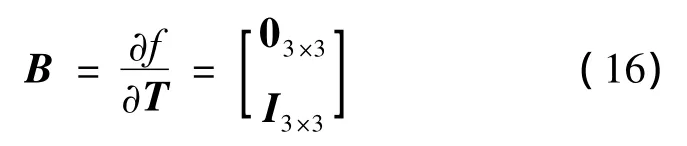
式(14)中:K为设计的反馈控制增益矩阵，η为调节系数，为实现优化过程中生成的推力避免处于最大和最小值。令T为推力向量T的大小，则η可定义为如下形式:

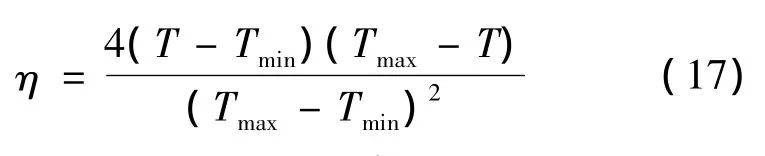
小天体着陆动力学对自旋角速度的敏感度向量如下所示:

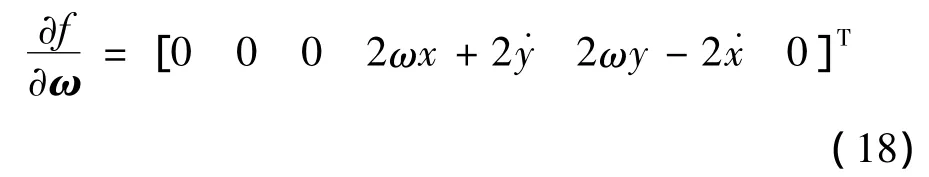
为了在优化过程中降低对参数的敏感度，需要建立含有敏感度的性能指标。本文选取如下形式的性能指标:

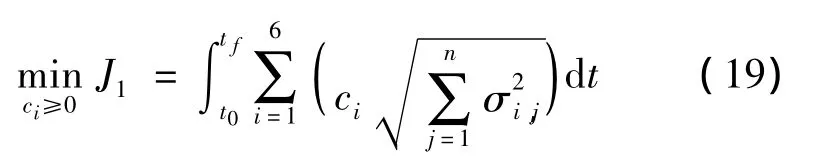
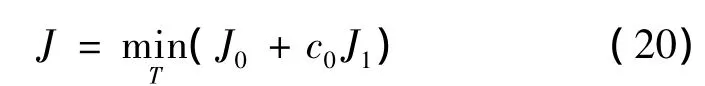
式中:c0≥0为调节敏感度和燃料的加权系数。至此，以J为性能指标进行优化，能在节省燃料的同时实现对参数不确定性不敏感。

3 仿真结果及分析

通过高斯伪谱法可以将上述轨迹优化问题转化为非线性规划问题，并采用SNOPT算法求解。仿真条件以Eros433小行星为目标着陆天体，其名义半径为16 km，引力常数为4．4621×105m3/s2，密度为2．67 g/cm3，标称自旋角速度为3．31 rad/s。选取探测器质量为300 kg，推力发动机的最大推力为

式中:n为敏感度矩阵的维数，σi，j为矩阵的第(i，j)个元素。ci，i=1，…，6为权重系数，用于平衡位置和速度的权重。

通过构建性能指标J1，则可将原燃料最优问题转化基于燃料/敏感度加权的闭环优化问题:20 N，比冲为300 s。探测器的初始和末端条件分别如表1所示。给定条件下，采用高斯伪谱法求得小天体着陆的燃料最优轨迹如图4所示，可以看出着陆轨迹能够满足初始和末端状态以及路径约束，其三轴速度变化过程如图5所示，在无参数摄动情况下，着陆器能够平稳着陆到小天体表面，到达目标点。在着陆过程中，着陆器三轴推力及其合理大小如图6所示。从中可以看出，燃料最优着陆轨迹的合力大小为bang－bang形式。由于推力长时间处于最大边界，在存在参数不确定性及初始状态偏差的情况下，控制系统极易饱和，难以达到抑制偏差的目的。

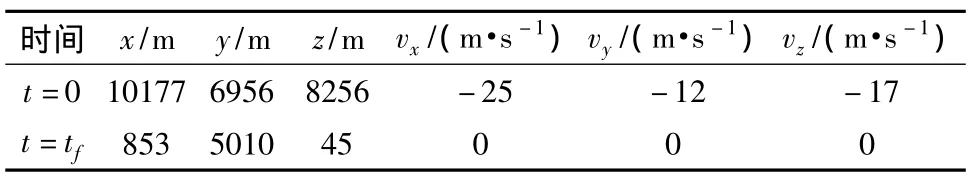
表1 边界条件Table 1 Boundary conditions

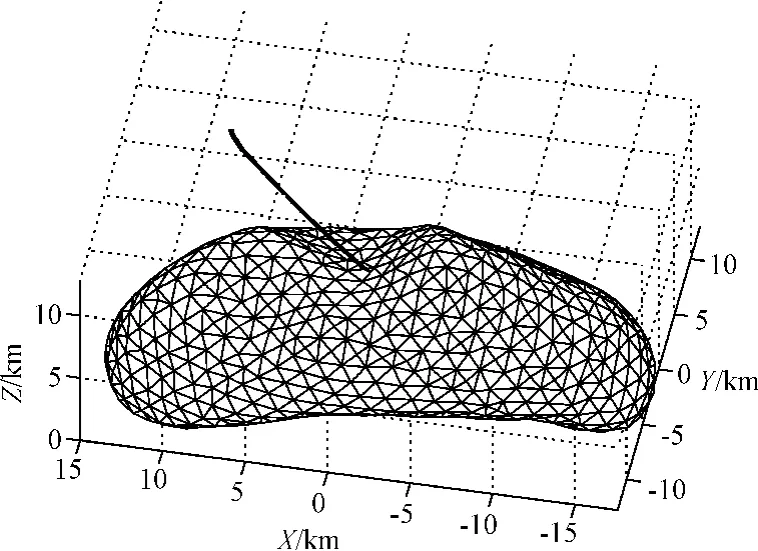
图4 燃料最优着陆轨迹Fig．4 Fuel optimal landing trajectory

图5 最优着陆轨迹的三轴速度Fig．5 Velocities of optimal trajectory in three axes direction

小天体着陆轨迹受参数不确定性及初始状态偏差的影响在文献［5］中进行了研究，着陆误差受探测器状态确定精度及推力器模型误差影响较大。因而，在无法确切获知目标天体参数及探测器状态信息的情况下，执行开环着陆会引起非常大的着陆误差，可能导致着陆任务的失败。

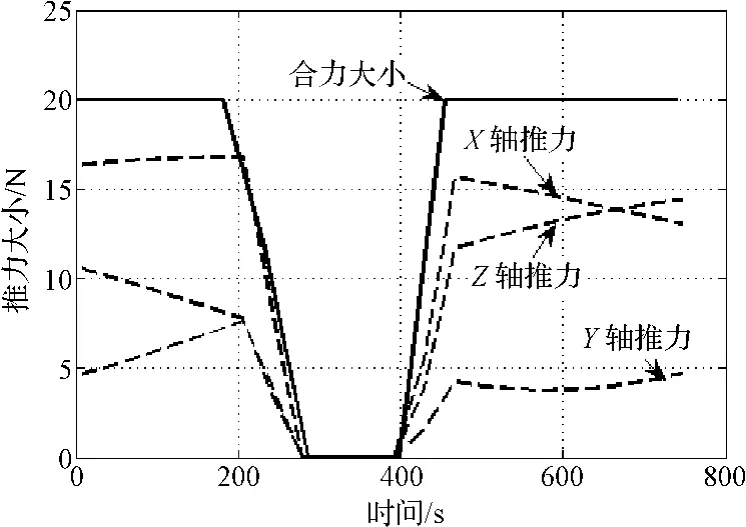
图6 三轴推力及合力大小Fig．6 Thrust in three axes and its net thrust

引入闭环敏感度性能指标J1，则通过优化推力大小和方向能够降低燃料消耗和敏感度，获得的推力曲线如图7所示，通过调节加权系数c0能够调节敏感度性能指标J1的比重。当c0逐渐增大时，推力曲线逐渐接近远离最大最小边界，从而留有一定的控制余量用于抑制参数不确定性和初始状态偏差的影响，能够有效避免控制系统饱和，达到提高着陆精度的目标。在实际着陆任务中，需根据目标天体参数不确定性和初始状态偏差范围合理选取c0，达到既能节省燃料又能实现提高着陆精度的目标。

表2 状态和参数不确定性范围Table 2 Dispersions in states and parameters

为了校验基于燃料/敏感度加权的闭环优化方法对参数不确定性和初始状态偏差的抑制效果，另外进行了一组2000次Monte Carlo仿真。其中，小天体着陆动力学存在的参数不确定性及探测器初始状态偏差范围如表2所示。

在给定参数范围下，最终着陆位置和速度误差分别如图8和图9所示。其中，图8为着陆位置误差结果，其3σ 误差椭圆为0．21 m×0．68 m，能够满足小天体精确着陆的位置精度要求。另外，小天体引力非常小，较大的速度与小天体表面碰撞可能使得达到小天体的逃逸速度，因而小天体着陆任务对着陆速度误差有非常高的要求。图9所示的着陆速度显示最终的着陆速度均小于0．1 m/s，能够满足在小天体表面着陆的速度要求。

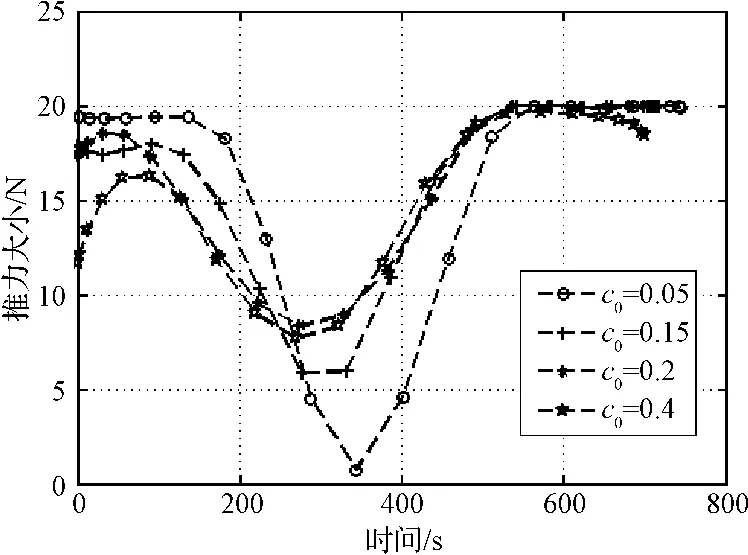
图7 着陆轨迹的推力大小Fig．7 Thrust magnitude of optimal trajectory

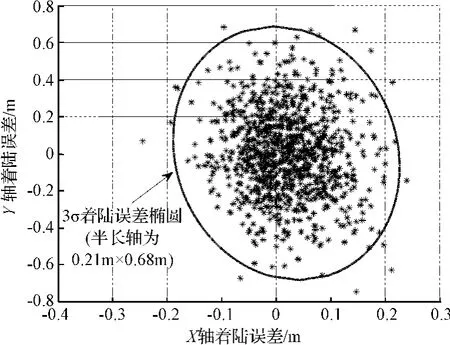
图8 着陆位置误差及误差椭圆Fig．8 Position error and its error ellipse

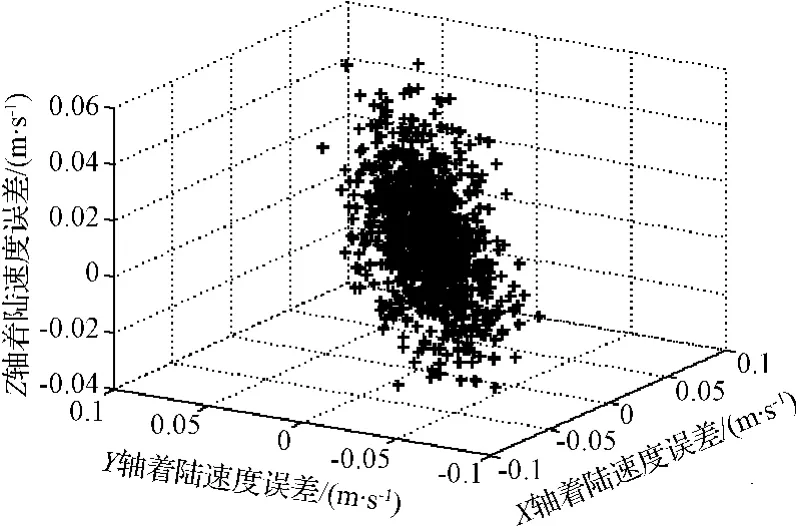
图9 三轴着陆速度误差Fig．9 Velocity error in three axes

4 结束语

本文针对小天体着陆动力学存在的参数不确定性及探测器初始状态的偏差对着陆误差的影响，提出了一种考虑跟踪制导的小天体着陆闭环优化方法。该方法综合考虑了小天体着陆的燃料消耗和动力学模型对参数和状态不确定性的敏感度，能够实现着陆过程既节省燃料，又降低参数和状态不确定性的敏感度。仿真结果显示，在给定参数不确定性和初始状态偏差条件下，跟踪着陆轨迹的3σ位置误差椭圆为0．21 m×0．68 m，速度误差均小于0．1 m/s，能够满足小天体精确着陆的任务要求。

［1］ 崔平远，乔栋，朱圣英，等．行星着陆探测中的动力学与控制研究进展［J］．航天器环境工程，2014，31(1):1－8．［Cui Ping-yuan，Qiao Dong，Zhu Sheng-ying，et al．Research progress of dynamics and control for planetary landing［J］．Spacecraft Environment Engineering，2014，31(1):1－8．］

［2］ 乔栋，黄江川，崔平远，等．嫦娥二号卫星飞越探测小行星的目标选择［J］．中国科学:技术科学，2013，43(6):602－608．［Qiao Dong，Huang Jiang-chuan，Cui Ping-yuan，et al．Target selection to fly by asteroid exploration for Chang’E－2 mission［J］．Science China Technological Sciences，2013，43(6):602–608．］

［3］Cheng A F，Santo A G，Heeres K J．Near-Earth Asteroid Rendezvous:mission overview［J］．Journal of Geophysical Research:Planets，1997，102(10):23695–23708．

［4］Yoshimitsua T，Kawaguchia J，Hashimotoa T．Hayabusa-final autonomous descent and landing based on target marker tracking［J］．Acta Astronautica，2009，65(5):657－665．

［5］Broschart SB，Scheeres D J．Spacecraft descent and translation in the small-body fixed frame［C］．AIAA/AAS Astrodynamics Specialist Conference，Rhode Island，August 16－19，2004．

［6］ 袁旭，朱圣英，乔栋，等．小天体着陆动力学参数不确定性影响分析［J］．深空探测学报，2014，1(2):134－139．［Yuan Xu，Zhu Sheng-ying，Qiao Dong，et al．Impact analysis of dynamic parameters uncertainty on small celestial body landing［J］．Journal of Deep Space Exploration，2014，1(2):134－139．］

［7］ 黄翔宇，崔平远，崔祜涛，等．利用Gauss-Markov过程的着陆小天体导航与制导方法［J］．宇航学报，2004，25(3):338-342．［Huang Xiang-yu，Cui Ping-yuan，Cui Hu-tao，et al．A navigation and guidance method for small celestial body landing using Gauss-Markov process［J］．Journal of Astronautics，2004，25(3):338－342．］

［8］ 崔平远，朱圣英，崔祜涛．小天体软着陆自主光学导航与制导方法研究［J］．宇航学报，2009，30(6):2159－2164．［Cui Ping-yuan，Zhu Sheng-ying，Cui Hu-tao．Autonomous optical navigation and guide method for soft landing on small bodies［J］．Journal of Astronautics，2009，30(6):2159－2164．］

［9］Furfaro R，Cersosimo D，Wibben D R．Asteroid precision landing via multiple sliding surfaces guidance techniques［J］．Journal of Guidance，Control，and Dynamics，2013，36(4):1075－1092．

［10］ 崔平远，朱圣英，崔祜涛．小天体自主软着陆脉冲机动控制方法研究［J］．宇航学报，2008，29(2):511－516．［Cui Ping-yuan，Zhu Sheng-ying，Cui Hu-tao．Autonomous impulse maneuver control method for soft landing on small bodies［J］．Journal of Astronautics，2008，29(2):511－516．］

［11］Carson J M，Acikmese B，Murray R M，et al．A robust model predictive control algorithm augmented with a reactive safety mode［J］．Automatica，2013，49(5):1251－1260．

［12］Lantoine G．Optimal trajectories for soft landing on asteroids［R］．MS Special Problems Report，Georgia Institute of Technology，Atlanta，2006．

［13］ 江秀强，陶婷，杨威，等．附着小天体的最优制导控制方法［J］．深空探测学报，2015，2(1):53－60．［Jiang Xiu-qiang，Tao Ting，Yang Wei，et al．Optimal guidance control strategies for spacecraft attaches to a small body［J］．Journal of Deep Space Exploration，2015，2(1):53－60．］

［14］ 任高峰，高艾，崔平远，等．一种燃料最省的火星精确着陆动力下降段快速轨迹优化方法［J］．宇航学报，2014，35(12):1350－1358．［Ren Gao-feng，Gao Ai，Cui Ping-yuan，et al．A rapid power descent phase trajectory optimization method with minimum fuel consumption for Mars pinpoint landing［J］．Journal of Astronautics，2014，35(12):1350－1358．］

［15］Avinash P，James F，Raktim B．Polynomial chaos-based analysis of probabilistic uncertainty in hypersonic flight dynamics［J］．Journal of Guidance，Control，and Dynamics，2010，33(1):222－234．

［16］Park R S，Scheeres D J．Nonlinear mapping of Gaussian statistics:theory and applications to spacecraft trajectory design［J］．Journal of Guidance，Control，and Dynamics，2006，29(6):1367－1375．

［17］Zimmer SJ．Reducing spacecraft state uncertainty through indirect trajectory optimization［D］．Austin:The University of Texas at Austin，2005．

［18］Kreindler E．Formulation of minimum trajectory sensitivity problem［J］．IEEE Transactions on Automatic Control，1969，14(2):206–207．

［19］Seywald H，Kumar R R．Desensitized optimal trajectories［J］．Advances in the Astronautical Sciences，1996，93(1):103－116．