非线性H∞导引律设计与分析

刘利军，余 臻，沈 毅

(1．厦门大学自动化系，厦门361005;2．哈尔滨工业大学控制工程系，哈尔滨150001)

0 引言

导引律是反导导弹拦截系统制导子系统中非常重要的核心环节。随着反导导弹拦截系统的日益成熟，常规攻击导弹的威胁正在逐步降低，所以现阶段来袭攻击导弹向着高隐身性和强机动性的方向发展［1］。为了应对挑战，反导系统除了发展更好的测量手段外，也急需发展能够处理强测量噪声干扰和目标强机动的末端导引律，并且需要对此导引律的末端导引机理进行深入分析［2］。

比例导引律及其变种(纯比例导引律、真比例导引律、扩展比例导引律等)［3－4］是被广泛使用的、较为简洁的一类导引律，但是它们缺乏应对强噪声干扰和目标强机动的理论基础和实际效果［2－4］。因此，各种现代控制理论被应用于导引律的设计，例如分数阶修正比例导引律［5］、滑模变结构导引律［6－8］、鲁棒导引律［9－11］，最优导引律［12］，反馈线性化［13］，有限时间收敛导引律［14－15］，目标估计导引律［16］等。特别地，文献［6］利用高阶滑模控制器和观测器设计了能够处理强机动目标的导引律，具有较强鲁棒性;文献［9］考虑导弹控制系统动态特性及其不确定性，利用分块反步设计思想，结合输入——状态稳定性理论，设计了一种三维非线性鲁棒导引律;文献［16］采用高增益观测器估计目标的机动，并且将估计信息补偿到导引律设计中;文献［14］利用非线性控制系统有限时间稳定性理论得到了有限时间收敛变结构导引律，证明了在弹目相对速度为常数、目标在一定机动条件下，该导引律保证视线角速率在末制导结束前收敛到零;文献［11］和我们的工作［10］针对未知目标机动，设计了非线性H∞导引律，但是没有充分考虑测量噪声的影响。在已有的大量研究资料中，缺乏将测量噪声和目标机动放置于统一框架和系统下的讨论和设计工作，往往顾此失彼，而且参数的变化与导引品质的关系不明确，不利于针对不同的目标和场景优化导引律。这两个问题是本文将要研究的主要内容。

本文的主要工作是建立了考虑测量噪声和目标机动的简单的三维弹目相对运动系统方程;进而利用非线性H∞控制理论构造相应的Hamilton-Jacobi-Isaacs(HJI)偏微分方程不等式，并且给出了求解方法，得到了一组解析解和正定的储能函数，成功设计了非线性H∞导引律;在此基础上分析了导引律设计参数与几项制导拦截关键因素的定性关系;最后仿真研究验证了非线性H∞导引律的有效性和定性分析的有效性。

1 改进极坐标下三维弹目相对运动方程

导弹与目标的相对运动如图1所示，弹目相对位置矢量为r，方向沿视线方向由导弹指向目标为正，rT，rM分别是目标与导弹在惯性坐标系的位置矢量，于是有

式中:r是弹目之间的距离，er是视线方向的单位矢量。对式(1)求导可得弹目相对速度方程与相对加速度方程如下:

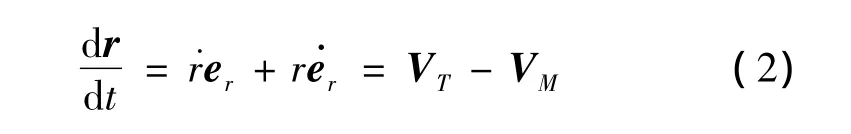
图1 三维弹目相对运动示意图Fig．1 Illustration of three-dimensional relative motion between a missile and a target

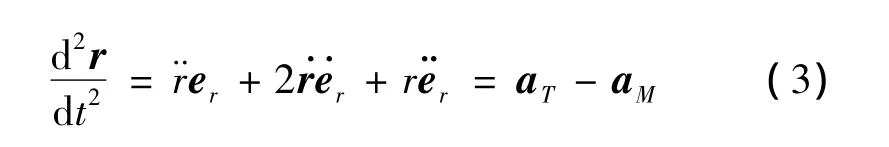
式中:VT，aT，VM，aM分别是目标与导弹的速度与加速度矢量。

设视线的旋转角速度矢量为Ω，Ω的方向与视线方向垂直。利用运动学相关知识，可得e

r及定义如下单位向量:

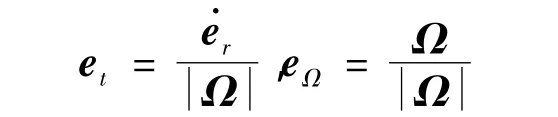
这样(er，et，eΩ)就构成改进的极坐标系(Modified Polar Coordinate，MPC)，是正交坐标系，且满足右手定则。显然MPC坐标系是活动坐标系。

将目标与导弹的加速度矢量aT与aM在MPC坐标系(er，et，eΩ)下分解:

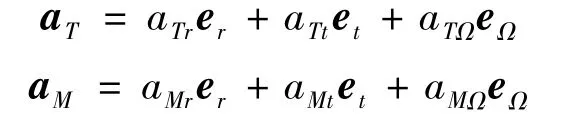
计算式(3)，可得如下三维非线性弹目相对运动方程:

在MPC坐标系下，上述非线性常微分方程组描述了三维弹目相对运动，将传统的极坐标下的6个非线性常微分方程组简化为3个较简单的常微分方程组，更加易于分析和设计。在MPC坐标系下求得的导引律(主要是aMt)，可以通过视线的角速度矢量直接转换为固定坐标系下的三维导引律［17］。

2 非线性H∞导引律设计

由于视线转率是否收敛决定了反导导弹能否命中目标，所以导引律的设计原则主要是零化视线转率，所以只需要关注式(4)中有关视线转率动态过程的第二个方程，即这是一个理想的视线转率动态方程，但在实际的制导回路中都会有测量误差。

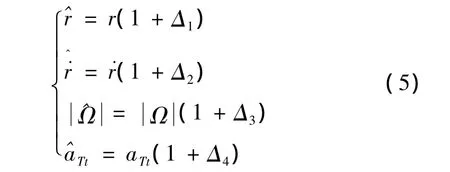
式中:i=1，2，3，4。令 α 为测量噪声 Δ2+Δ3的统计期望且，并且进一步可化解可得:

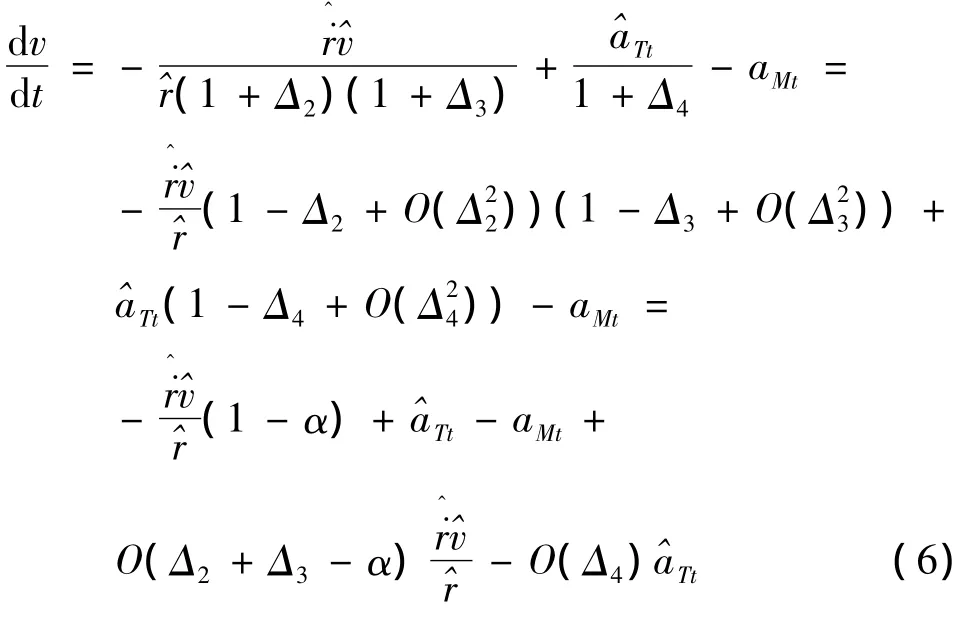
在此基础上，设计非线性三维H∞导引律，构造评价法向速度和导弹控制的代价函数如下:z=，其中k和ρ是给定常数。

应用非线性H∞控制理论，可构造如下的Hamilton-Jacobi-Isaacs(HJI)偏微分方程不等式:

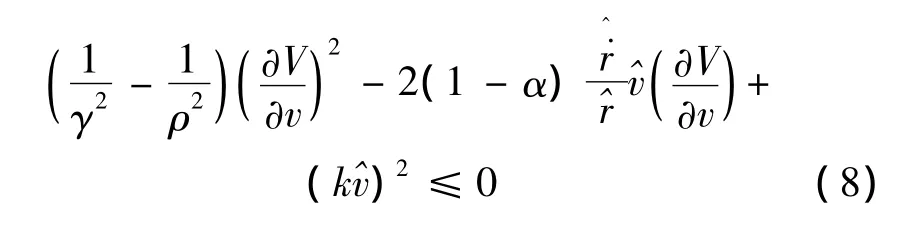
式中:γ＞0表示w到z的系统L2增益的上界。将式(8)看作的普通二次不等式，等号成立有两根:

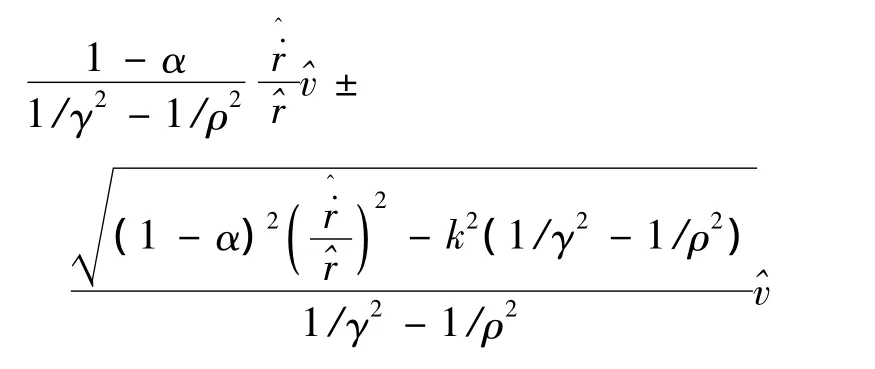
显然，要使式(8)全局成立并且保证两根为实数，要求γ＞ρ。故使得式(8)全局成立的为:

因为要求储能函数V(v)是一个正定函数，所以要求β＜－1。通过以上设计和分析过程，我们给出了式(8)的一个解集，那么系统(7)的非线性三维H∞导引律可以构造如下:

3 非线性H∞导引律拦截目标分析与讨论

假设导弹的拦截能力和其他拦截条件已经确定，我们讨论导引律(10)的参数与导引品质的一些定性关系。

我们主要讨论制约导引品质的几项关键要素:1)测量噪声、干扰;2)目标机动能量和形式;3)导引初始条件。

2)目标机动能量和机动形式是目标突防的主要指标和手段。由于现有技术手段对目标的加速度估计往往误差较大，所以目标机动能量体现在，通过设计评价函数能量和调节γ，在导弹过载未饱和条件下，保证在导引律(10)的控制下，目标机动能量不会引起拦截失败。目标在相同能量条件下，不同的机动形式对拦截有非常大的影响，两种常见强机动形式为:a)目标的机动显著改变弹道，例如常值机动、微分对策机动;b)目标的机动造成目标在某个小范围内改变运动轨迹，例如正弦机动，螺旋机动，正反向开关机动等周期机动。第一种情况因为弹道变化显著，攻击任务可变，甚至反向逃走，所以不宜拦截，但是导弹一般不会进行这类大范围机动(常见于飞机)，不是我们讨论的重点。第二种情况是正在发展的导弹末端欺骗机动，主要作用是拦截末端造成视线转率的剧变，甚至发散，主要影响是在拦截末端显著增大式(7)中的未知干扰w，这就要求导引律具有很强的鲁棒性。在导引律设计过程中，可以通过增加评价函数中k的值提高法向速度的权重，增强视线转率收敛的权重;另外，β若等于 －1，则代表HJI不等式等号成立，为最优非线性H∞导引律，减小β的值可以平衡系统的最优性和鲁棒性的设计侧重点。所以，增加k和减小β都可以显著提高系统的鲁棒性，有效对抗目标的末端机动。

3)导引的初始条件是导弹拦截性能和导弹发射时间窗口的重要指标，往往用捕获区域刻画，但是捕获区域与导引律和三维相对运动方程密切相关，很难直接推导获得。而根据非线性耗散性理论和非线性H∞控制理论，在非零初始状态下，导引律(10)保证系统能量满足关系式V(v(t))－V(v(0))≤，由于拦截成功意味着v(t)→0，即V(v(t))→0，所以能量关系式主要是 －V(v(0))，根据导弹自身的能力可以估算出，进而估算出使能量关系式成立的v(0)的范围，或者给定初始条件v(0)，判断能量关系式是否成立或成立的概率，可以简单直观地确定导弹成功拦截的初始导引条件。

4 仿真研究与验证

将导弹的动态环节近似为一个时间常数为T=0．1 s的一阶环节，测量状态的误差 Δ1，Δ2，Δ3同为均值－0．05、方差0．03的有色噪声，目标的加速度估计误差Δ4为均值0．1、方差0．05的有色噪声。采用FIR-Equiripple低通滤波器对噪声进行处理，通带频率为200π(rad/s)，阻带频率为400π(rad/s)，处理后的数据被提供给制导环节中的以及。

拦截的初始条件为:导弹位置原点(0，0，0)，导弹初速度600 m/s，导弹发射的方位角为π/4 rad，高低角为0．7 rad，导弹的法向过载限制为300 m/s2;目标位置(10000 m，10000 m，10000 m)，目标的来袭速度为1500 m/s，目标来袭的方位角为5π/4 rad，高低角为 －2．44 rad，向着原点附近攻击。当弹目最小距离小于0．15 m时，表示拦截成功，否则拦截失败。

给定导引律(10)中的参数为:α=－0．1，β=－1．5，k=0．5，ρ=0．8，γ=1，则导引律为:

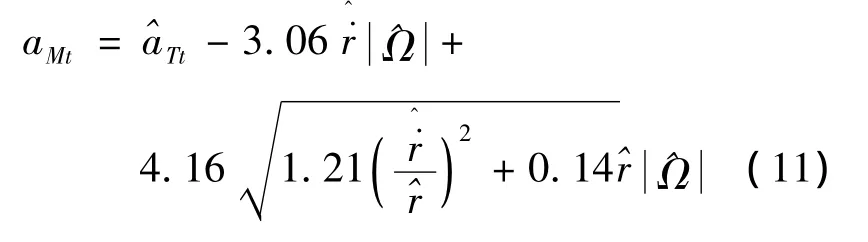
我们采用PN(Proportional Navigation)导引律进行对比，PN导引律在MPC坐标系下的解析形式为:

式中:c＞2为可调节参数，经过多次仿真试验优化，我们选取c=5。

仿真1:目标在垂直视线方向做大小为180 m/s2、周期为3 s、占比50%的方波机动，如图2中的细实线所示。分别采用非线性H∞导引律(11)和PN导引律(12)进行制导控制拦截，脱靶量分别为0．13 m和36 m，即非线性H∞导引律成功拦截目标，而PN导引律(12)脱靶。

其他拦截信息如图2和图3所示:图2中的粗实线(NH)显示了非线性H∞导引律的导弹实际加速度，充分利用了导弹的过载能力，而且对目标的机动做出了快速响应;图2中的粗虚线(PN)显示了PN导引律的导弹实际加速度，其峰值严重滞后于目标机动，造成脱靶;图3显示了两张导引律的视线转率变化，粗实线(NH)代表非线性H∞导引律控制下的弹目视线转率变化，其收敛迅速，能够稳定跟踪目标的机动;而图3中的粗虚线(PN)代表PN导引律控制下的弹目视线转率变化，最终发散。

图2 仿真1:两种导引律下导弹和目标的加速度Fig．2 Simulation 1:accelerations of the missile and the target for two different guidance laws

仿真2:改变目标机动的形式:目标在垂直视线方向做大小为180 m/s2、周期为4 s、占比50%的方波机动，如图4中的细实线所示。仿真结果如图4和图5所示。虽然这次目标的机动能量与仿真1中的机动能量大致相同，但是导弹在非线性H∞导引律(11)的控制下已经无法命中目标，视线转率发散，当然PN导引律也无法命中目标，视线转率发散。两者的脱靶量都在2000 m以上。

图3 仿真1:两种导引律下视线转率的变化Fig．3 Simulation 1:the turning rate of line of sight for two different guidance laws

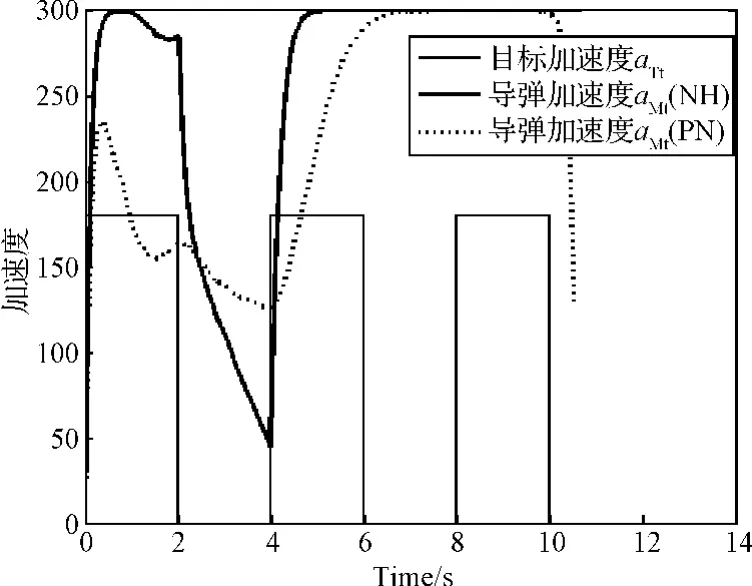
图4 仿真2:两种导引律下导弹和目标的加速度Fig．4 Simulation 2:accelerations of the missile and the target for two different guidance laws

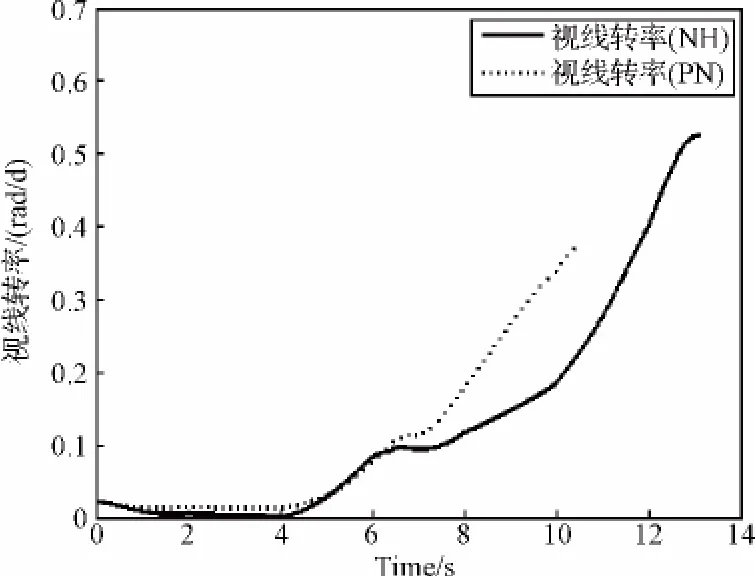
图5 仿真2:视线转率的变化Fig．5 Simulation 2:the turning rate of line of sight

仿真3:仍然采用仿真2的目标机动环境。分析仿真2失败的原因可知，虽然目标的加速度能量相同，但是引起了目标弹道的较大未知变化，需要提高导引律的鲁棒性来拦截目标。因此，将β和K的值相对调高，β=－6，k=1，计算得非线性H∞导引律为:

同样，为了提高PN导引律拦截强机动目标的能力和鲁棒性，进一步调整优化PN导引律的参数，经反复测试，令c=10，即

利用以上PN导引律和非线性H∞导引律(13)，我们分别对仿真1和仿真2中的目标机动情况进行了拦截，PN导引律都拦截失败，而非线性H∞导引律(13)都拦截成功。对仿真1目标的拦截结果与图2和图3所示结果相似，主要区别是导弹的加速度更大、变化更剧烈一些。对仿真2目标机动的拦截脱靶量分别为0．11 m和490 m，非线性H∞导引律(13)拦截成功，而PN导引律拦截失败。导弹加速度和视线转率变化如图6和图7所示，可见本文提出的非线性H∞导引律设计方法能充分跟踪处理目标强机动，抑制视线转率发散，具有一定的优越性。

图6 仿真3:两种导引律调整参数后的导弹和目标的加速度Fig．6 Simulation 3:accelerations of the missile and the target for two different guidance laws with adjusted parameters

5 结束语

图7 仿真3:两种导引律调整参数后的视线转率的变化Fig．7 Simulation 3:the turning rate of line of sight for two different guidance laws with adjusted parameters

本文采用非线性H∞控制理论对存在测量误差和干扰的三维导弹拦截系统设计了具有严格解析形式的非线性H∞导引律。首先，构建基于改进极坐标系下的三维弹目相对运动方程，极大了简化了传统三维弹目相对运动方程的复杂性;其次，建立了存在多种测量噪声和干扰下的弹目相对运动方程，紧紧抓住导弹拦截的本质(v→0)，进而归纳出简洁的导弹拦截目标的系统方程;然后，利用非线性H∞控制理论构造了HJI偏微分方程不等式，一般情况下HJI偏微分方程不等式是很难求解的，特别是得到一个解析解，但是由于我们合理简化了导弹拦截系统方程，所以我们能够求得一组HJI偏微分方程不等式的解析解，同时构造了相应的正定储能函数，进而构造了非线性H∞导引律;接着，通过分析导弹拦截目标的几个关键因素，以及分析这些因素与非线性H∞导引律设计参数的关系，定性指出了如何调整参数能够有效对抗各种不利因素，提高制导性能;最后，通过仿真进一步研究验证了非线性H∞导引律的有效性和定性分析的有效性。

本文的非线性H∞导引律设计可以处理制导过程中测量噪声与干扰、目标机动、导弹机动与目标机动能量比限制、导弹过载限制、初始导引条件限制等多方面的问题，但是很多关系仍然是定性形式或者不够精确，所以需要进一步研究确切的解析形式的严格数学关系，提高导引律设计和调整参数的效率，提高导引品质。

［1］Gutman S．Applied min-max approach to missile guidance and control［R］．AIAA:Progress in Astronautics and Aeronautics，Vol．209，2005．

［2］Shneydor N A．Missile guidance and pursuit:kinematics，dynamics and control［M］．Cambridge:Wood Publishing Limited，1998．

［3］Yang C D，Yang C C．A Unified approach to proportional navigation［J］．IEEE Transactions on Aerospace and Electronic Systems，1997，33(2):557－567．

［4］Tyan F．Unified approach to missile guidance laws a 3D extension［J］．IEEE Transactions on Aerospace and Electronic Systems，2005，41(4):1178－1199．

［5］ 朱竹婷，廖增，彭程，等．一种分数阶修正比例导引律［J］．控制理论与应用，2012，29(7):945－948．［Zhu Zhu-ting，Liao Zeng，Peng Cheng，et al．A fractional-order modified proportional navigation law［J］．Control Theory＆Applications，2012，29(7):945－948．］

［6］Kada B．Arbitrary-order sliding-mode-based homing-missile guidance for intercepting highly maneuverable targets［J］．Journal of Guidance，Control，and Dynamics，2014，37(6):1－15．

［7］ 周狄．寻的导弹新型导引规律［M］．北京:国防工业出版社，2002．

［8］Liang Y W，Chen C C，Liaw D C，et al．Robust guidance law via integral-sliding-mode scheme［J］．Journal of Guidance，Control，and Dynamics，2014，37(3):1038－1042．

［9］ 严晗，季海波．弹道坐标中三维鲁棒非线性导引律［J］．控制理论与应用，2013，30(9):1079－1085．［Yan Han，Ji Haibo．Three-dimensional robust nonlinear guidance law in trajectory coordinates［J］．Control Theory＆Applications，2013，30(9):1079－1085．］

［10］Liu L J，Shen Y．Three-dimension H∞guidance law and capture region analysis［J］．IEEE Transactions on Aerospace and Electronic Systems，2012，48(1):419－429．

［11］Chen H Y，Yang CD．Three-dimensional H∞nonlinear guidance law［J］．International Journal of Robust and Nonlinear Control，2001，11(2):109－129．

［12］ 刘利军，沈毅，赵振昊．基于多项式拟合SDRE的三维导引律设计［J］．宇航学报，2010，31(1):87－92．［Liu Li-jun，Shen Yi，Zhao Zhen-hao．Three-dimensional missile guidance law design based on polynomial fitting of SDRE［J］．Journal of Astronautic，2010，31(1):87－92．］

［13］Alkaher D，Amiram M，Yizhar O．Guidance laws based on optimal feedback linearization pseudocontrol with time-to-go estimation［J］．Journal of Guidance，Control，and Dynamics，2014:37(4):1－7．

［14］ 孙胜，周荻．有限时间收敛变结构导引律［J］．宇航学报，2008，29(4):1258－1262．［Sun Sheng，Zhou Di．A finite time convergent variable structure guidance law［J］．Journal of Astronautics，2008，29(4):1258－1262．］

［15］ 丁世宏，李世华，罗生．基于连续有限时间控制技术的导引律设计［J］．宇航学报，2011，32(4):727－733．［Ding Shihong，Li Shi-hua，Luo Sheng．Guidance law design based on continuous finite-time control technique［J］．Journal of Astronautic，2011，32(4):727－733．］

［16］ 马克茂，贺风华，姚郁．目标机动加速度的估计与导引律实现［J］．宇航学报，2009，30(6):2213－2219．［Ma Ke-mao，He Feng-hua，Yao Yu．Estimation of target maneuver acceleration and guidance law implementation in homing terminal guidance［J］．Journal of Astronautics，2009，30(6):2213－2219．］

［17］ 刘利军．导弹末端导引机理及信号滤波研究［D］．哈尔滨:哈尔滨工业大学，2009．［Liu Li-jun．Research on missile terminal guidance law and signal filtering［D］．Harbin:Harbin Institute of Technology，2009．］