谈三视图的教学

王浩

把三视图列为初中数学教学中的必学内容也是这一轮课改中一个突出的亮点.由于教师自身的知识结构（多数教师没有学过机械制图）和缺乏教学经验等原因，如何落实好课标中规定的关于三视图教学的各项目标，很多教师都感到困难.本文就三视图教学的意义，三视图的概念、画法及应用等方面的教学，谈谈个人的一些经验和体会.

一、正确认识三视图教学的意义

三视图作为“图形与几何”领域的内容之一，它与其他“图形与几何”的内容一样，在培养学生的空间观念和发展空间想象能力方面有着重要的作用.且三视图教学中这方面的作用表现为这样的一种特性：让学生逐步适应、并学会三维与二维的空间形式的转换.

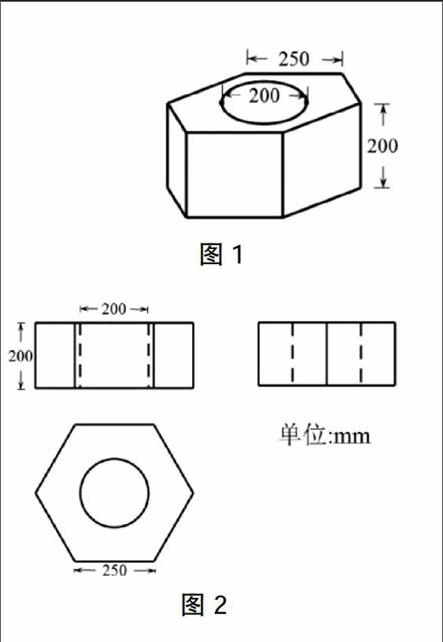
三视图是设计者与制作者之间相互沟通交流的一种不可替代的语言.如设计人员要把他设计的一个螺帽毛坯形状、尺寸要求告诉工人，把螺帽毛坯画成如图1那样的立体图. 此图虽然很有立体感，但仍然无法把螺帽毛坯的底面、侧面是怎样的几何图形、中间的圆孔与整个毛坯有怎样的位置关系等说清楚. 只有用图2那样的三视图，才能清楚地说明螺帽外形是一个正六棱柱，正中位置有一个上下穿透的圆柱形的孔.也正因为三视图的这种独特功能，使它在人们生产、生活实践中有着广泛的应用.

也许有人认为三视图的内容太专业化，质疑作为基础教育的数学教学的必学内容是否合适？对此我们还需从我国教育事业的发展来认识，近几年来我国职业教育有了迅速的发展，升入职业高中的学生与普通高中学生比例已经达45.06∶54.94（2013年数据）.三视图这部分内容对升入职业高中的许多学生来说则是十分重要的基础课程，从这个角度来看，把三视图列为初中数学的必学内容也是我国教育事业发展新格局的需要.

我们在教学中应努力使学生认识学习三视图的重要性，这样就能调动学生学习三视图的积极性.

二、正确解读三视图的概念

在这轮课程改革的初期，不少教材把三视图解释成人们观察物体时，从正面、上面、左面三个不同方向看到的图形，这种说法是不正确的. 这种模糊解释给学生画三视图、识读三视图带来许多困难.

用正投影来定义三视图才是唯一正确的方法. 同样都从同一个方向去观察一个圆柱体，不同的人观察到的图形可能是不同的，而当圆柱体与投影面的相对位置确定的情况下，圆柱体在投影面上的正投影则是唯一确定的，这可以通过实验来验证，如图3.

同样也只有用物体在正投影面、侧投影面、水平投影面上的正投影，并在把三个投影面旋转展平（如图4）后所得的平面图形来定义三视图，才能得到. 使学生理解画三视图的基本法则：长对正，高平齐，宽相等.在这轮课改的初期不少教材连这条画三视图的基本法则都没有给出.

在讲解三视图概念时必须讲清楚以下三点：

（1）每一个视图分别是物体在哪一个投影面上的正投影.

（2）三个视图的相对位置，如图4.值得注意的是有些教辅读物、甚至是中考题把三个视图画在同一水平线上（如图5），这会对学生正确理解三视图的概念造成负面的影响.

（3）图4中三个视图的相对位置是要符合“长对正，高平齐，宽相等”的画法法则.

讲视图的概念必然要涉及空间点、线、面的位置关系，对这些关系应采用实验、实例等合情推理的方法使学生认同. 切忌用像立体几何中那样严格的推理方法.例如，我们可以用电线杆与地面的位置关系的实例来帮助学生认识投射线与投影面的垂直，而不去追究直线与平面垂直的定义.

增加一些辨认三视图与视图之间点、线、面之间对应关系的训练，对理解三视图的概念是很有帮助的.

案例1  一个几何体和它的三视图如图6.请完成下面的填空：

（1） 几何体中棱B1B2，A1B1在主视图中的正投影分别是           、           .

（2）几何体中棱A2D2在主视图、俯视图、左视图中的正投影分别是           、            、           .

（3） 几何体中侧面B1C1C2B2在主视图、俯视图、左视图中的正投影分别是           、            、

.

（4）主视图中矩形PQKJ是几何体中侧面

的正投影，正投影为左视图中矩形的边XS的几何体的面是            .

（5）三视图中与线段SU相等的线段是           .

三、掌握画三视图、识读三视图的关键

正确理解三视图的正投影本质，搞清三个视图之间的关系，以及它们与实物之间的对应关系是正确画三视图，识读三视图的关键所在.讲解这些关系要着重讲清以下两个方面.

（1）尺寸关系：也就是要遵循“长对正、高平齐、宽相等”.

（2）方位关系：方位关系指的是每个视图的上、下、左、右，分别表示物体的哪一个方位.具体的说：主视图的上、下表示物体的上、下，主视图的左、右表示物体的左、右;俯视图的上、下表示物体的后、前，俯视图的左、右表示物体的左、右;左视图的上、下表示物体的上、下，左视图的左、右表示物体的后、前，如图7所示.endprint

案例2   用一个过两条母线的平面截一个圆柱所得几何体如图8.请画出三视图，并在三视图上标出相应尺寸.

分析：画三视图通常先选一个合适的主视方向，选取的依据是如何使主视图、俯视图简明、易画. 本题可选图8中的正视的方向为主视方向，那么俯视图就是和几何体底面相同的一个弓形.由立体图中的尺寸可得这个弓形弦所对的圆心角为120°，这样就很容易画出俯视图.画出俯视图后，根据“长对正、高平齐、宽相等”就可依次画出主视图、左视图.

解   所求三视图如图9.

注意：左视图矩形的水平方向的边长应画成和俯视图弓形的高相等.

案例3  由若干个单位立方体垒成的一个几何体的三视图如图10.请描述这个几何体的形状，尝试画出立体示意图.

解  由主视图、左视图，知这个几何体有三层.由俯视图，知底层有3个小立方体.由主视图、左视图，知这个几何体中间位置靠前有两层，第二层有一个小立方体，右边位置靠后有三层，第二、三层各有一个小立方体，画出立体示意图，如图11.

从上例可以看到，搞清各个视图与实物之间的方位关系是十分重要的.

为了更好地培养学生画三视图、识读三视图的能力，我们还可以进行一些补画三视图的训练.

案例4  已知一个几何体的主视图和俯视图如图12，请根据已知视图想象几何体的可能形状，并按照你的想象补画左视图.

这是一道开放题，它含了画三视图和识读三视图的两方面的训练，它既能帮助学生熟练掌握三视图的画图法则和三视图与物体的方位关系，又能培养学生丰富的想象力，且富有趣味.有意思的是教师给出的答案大多如图13，而学生给出的答案有六、七种之多，如图14等.

在三视图的教学中我们还可以增加一些实用性很强的案例，让学生感受三视图的魅力.

案例5  一家紧固件进出口公司收到国外一家公司订购球头螺栓的一份订单，订单中附上该螺栓的三视图（这里省略了左视图）如图15，制作的材料是不锈钢，订数为180000枚，该进出口公司接单后考虑到今后托运等环节的需要，要估算一下这批货物的总质量是多少？你能帮助该公司完成立这项任务吗？怎样完成？

分析：根据国外客商所给的图纸，我们可以判断这批螺栓的上部是球被一个平面截得的部分（叫做球缺），可以从网上查出它的体积计算公式是V= （3r2+h2）（r表示球缺的底面半径，h表示球缺的高），下部是一个圆柱.这样我们就可以求出每一个螺栓的体积，再查出所用材料不锈钢的密度约7.8g/cm3，于是就可以算出每个螺栓的质量，继而估计出整批货物的总质量.

解  由视图，知螺栓的上部是球缺，球缺的底面半径r=15mm，高h=4mm.球缺的体积V= （3r2+h2）= （3×152+42）= （mm3）.下部圆柱的底面半径r=5mm，高h=40mm，圆柱的体积V=πhr2=40×52×π=1000π.（ +1000π）÷1000×7.8÷1000×180000≈6442.7（kg）.也就是这批货物总质量约为6442.7kg.endprint