一道高考线性规划题引发的“变式题组”探究

金伟兵

高中数学的线性规划是放在必修5的不等式一章中，实际是非常特殊的多元函数在简易定义域上的一个简单性质——求最值问题.教材的定位是让学生初步了解运筹学的这一部分内容，为高等数学打下基础，同时也是为了解决一部分实际问题，培养学生数形结合、转化化归的基本数学思想.这部分内容因其出题灵活，同时易与其他知识点交汇而在高考中越来越受到重视.近年各地高考题或模拟题中非常喜欢考这样的一类数学模型即含参变动型.在解题过程中往往都涉及以下三个基本思想：数形结合、含参讨论以及转化化归.下面笔者就和大家一起来评析一道2014年高考题及与其相关联的变式题组.

一、典例分析

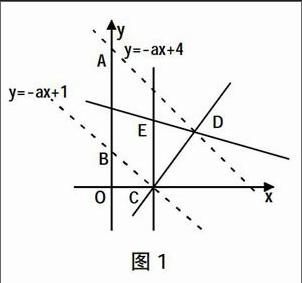
（2014年浙江理科数学）当实数x，y满足x+2y-4≤0，x-y-1≤0，x≥1时，1≤ax+y≤4恒成立，则实数a的取值范围是__________.

优美解：巧用数形结合.本题表面看是不等式恒成立问题，实际可转化为如图1所示的几何关系：即可行域三角形CDE区域应位于两平行直线y=-ax+1和y=-ax+4之间. 从而根据图象很快得到直线斜率

-a≥kAD且-a≤kBC，由kAD=- ，kBC=-1，从而得到答案a∈[1， ].

二、变式题组分析

1.（变式1） 追根溯源   原“型”毕露

（2008浙江理科数学）若a≥0，b≥0，且当x≥0，y≥0，x+y≤1时，恒有ax+by≤1，则以a，b为坐标的点P（a，b）所形成的平面区域的面积等于             .

简评：本题可转化为这样的几何意义：即可行域在直线y=- x+ 左下方，如图2所示.从而可得 ≥1， ≥1，再根据a，b为横纵坐标的图象可得平面区域是一个边长为1的正方形，则面积为1.由此可见浙江2014年的线性规划题和2008年的题颇有渊源，有异曲同工之妙.

2.（变式2） 转化化归   以静制动

（2013年北京理科数学）设关于x，y的不等式组2x-y+1>0，x+m<0，y-m>0，表示的平面区域内存在点P（x0，y0），满足x0-2y0=2，求得m的取值范围是（   ）

A. （-∞， ）         B. （-∞， ）

C. （-∞，- ）        D. （-∞，- ）

简评：本题可行域随m取值变动，但可转化为如图3所示的图形关系.

由图可知，可行域的边界点Q（-m，m）应位于直线y= x-1的下方，即满足 m<- m-1，从而得到m<- .本题解题时着眼点应该在x0-2y0=2这个条件，虽然线性约束条件变动，但实质的几何关系非常明显，即直线要“穿越”可行域，这样问题的切入点就很容易找到，“以静制动”，收得奇效.

3.（变式3）含参讨论   以动制静

（2013浙江理科数学）设z=kx+y，其中实数x，y满足x+y-2≥0，x-2y+4≥0，2x-y-4≤0.若z的最大值为12，则实数k=     .

简评：本题答案为2，可行域是固定区域，目标函数变动，可以结合图象根据k=0或k>0或k<0分别进行讨论. 此题重点考查了含参讨论思想，也是模拟题和高考题中很常见的题型. 要求学生具备比较好的分类讨论能力，同时应关注参数范围变化时最优解的位置变化，防止出错，“以动制静”，层次清晰.

4.（变式4）横向联系   综合串联

（2010安徽理科数学）设x，y满足约束条件2x+y+2≥0，8x-y+4≤0，x≥0，y≥0.若目标函数z=abx+y的最大值为8，求a+b的最小值为             .

简评：不等式表示的区域是一个四边形，4个顶点是（0，0），（0，2），（ ，0），（1，4），易发现目标函数在（1，4）取最大值8，所以8=ab+4？圯ab=4，接下去借助基本不等式性质得到：a+b≥2 =4，不等式在a=b=2时取到等号，所以a+b的最小值为4.线性规划与其他知识点的交汇，尤其是与不等式性质的综合交汇是近年高考题的新方向.

三、结束语

尽管高考题不断推陈出新，但其原型还是出自于我们平时的练习题. 所以在平时的教学中，如果我们能注意研究高考题的命题规律，分析题目之间的内在联系，进行有目的的变式题组训练，这样将会达到举一反三，触类旁通的作用，有效提升我们的教学效率.endprint