《数学实验》课程常微分方程求解的教学探索

□ 李 晔 李艳晴

数学实验是高等学校迎接21世纪数学教学改革的一门新课程，它将数学知识、数学建模和计算机应用三者有机结合在一起，使学生可以深入理解数学的基本概念、基本理论，熟悉常用数学软件，这样既培养了学生进行数值计算和数据处理的能力，也培养了学生应用数学知识建立数学模型、解决实际问题的能力，同时使学生真正做到了“学数学，用数学”，激发了学生学习数学的兴趣［1］。随着教学改革的不断深入，许多高校都在积极探讨数学实验的课程建设［2～3］、教学内容和教学方法［4］。实践表明，数学实验的重要性越来越被人们认识到，其研究方法也逐渐渗透到高校各大课程中。常微分方程求解是《数学实验》课程中的教学重点以及教学难点之一，本文根据多年教学经验，结合实际教学情况，探讨了数学实验课程中常微分方程求解的讲授方法。

一、教学方法研究

(一)借助实际案例提出问题，激发学生兴趣。教师在教学过程中，将数学建模思想融入到数学实验教学当中［5］，根据学生的知识基础提出问题，给出实验问题的背景介绍。比如，以实际案例“缉私艇追击走私船”出发，抓住学生胃口，吸引学生眼球，让学生带着问题而入，从而引出本节内容。这样不仅能让学生对建模思想有初步了解，培养学生创新能力，而且有助于加强学生的求知欲，提高学生的学习兴趣。

(二)由浅入深，由表及里，介绍龙格库塔法的思想。所谓数值方法，是将连续的微分方程的初值问题离散化为差分方程的初值问题，用差分方程的解近似代替微分方程的解［6］。常用的微分方程的数值解法有欧拉法、梯形公式、龙格库塔方法。本章主要是用龙格库塔方法编程序求解。为了便于学生掌握，由浅入深，由表及里，先从简单的方法(欧拉法、梯形公式)入手，然后导出龙格库塔方法。

微分方程的初值问题:

假设(1)式的解存在并且唯一(即ƒ(x，y)在矩形区域R={(x，y)|x0≤x≤xn，y0≤y≤yn}上连续，且关于 y 满足 Lipschitz条件)。

把定义域n等分，对微分方程y'=ƒ(x，y)在第i个小区间［xi，xi+1］上积分得:

对于(2)式中的定积分，用不同的数值方法(左矩形公式、右矩形公式、复合梯形公式)求解，便得到不同的求解常微分方程的数值方法(向前欧拉公式、向后欧拉公式、梯形公式)。

如，用左矩形公式求(2)中的定积分，得:

y(xi+1)≈y(xi)+hƒ(xi，y(xi))

又有 yi+1=y(xi+1)，yi≈y(xi)，所以 yi+1=y+hƒ(xi，yi)，i=0，1，…，即向前欧拉公式。显然，步长越小，结果越精确。

同理，用右矩形公式求(2)中的定积分，得y(xi+1)≈y(xi)+hƒ(xi+1，y(xi+1))，即向后欧拉公式，这是隐式格式，求解时需采用预测校正方法，即先用向前欧拉法提供初值，然后再用向后欧拉公式迭代，计算公式为:

用复合梯形公式求定积分，得数值解的计算公式为:

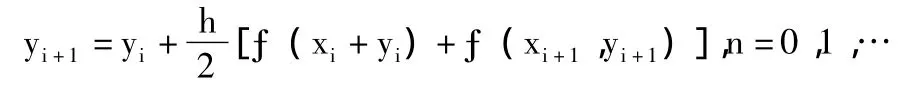
综上，欧拉公式在计算(2)中的定积分时只用到了一个点(左端点或右端点)处的导数值(即ƒ(x，y)值);梯形公式用了两个点(左、右端点)的导数值;在此基础上，在小区间［xi，xi+1］上多取几个点，计算这些结点处的导数值，然后作这些导数值的线性组合，构造近似公式，这就是龙格库塔法的基本思想。

常用的龙格库塔法有二级二阶R－K方法

在介绍各种数值方法时，可用Matlab进行仿真，把每一步迭代结果动态的反映到图像中，将抽象的算法直观地呈现在学生面前，加深学生的理解，激发学生的兴趣。

(三)用Matlab编程序求解。例:所求微分方程初值问题为，用龙格库塔法求解的程序为:

编写函数文件exf:

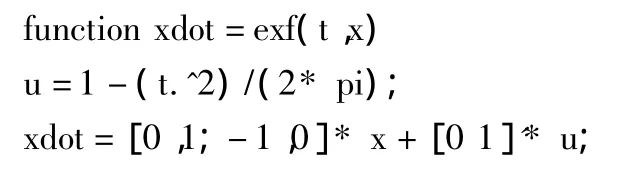
编写主程序:

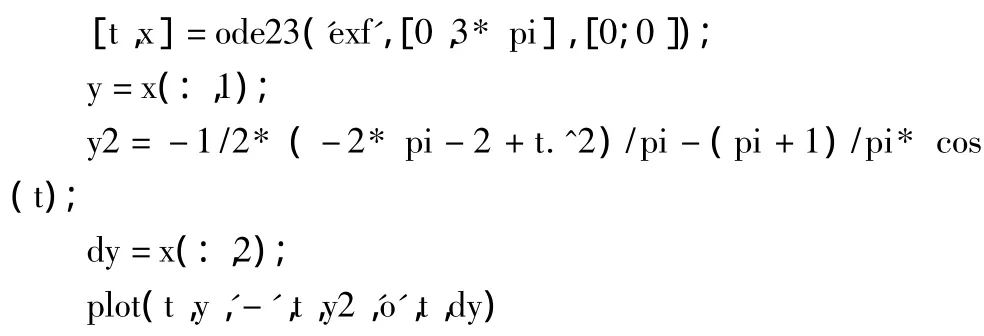
运行结果见图1。

图1 数值解与解析解

图2 simulink模块连接图

(四)建立Simulink模块连接图，进行比较式教学。首先建立方程的simulink模型，保存为 aa2．mdl，见图2。运行仿真:

仿真画出y及其导数的图像，结果同图1。

由上，simulink不需要学生对算法有很深的了解，只需画出模块连接图，就可以将结果可视化。而且，模拟是交互的，学生可以快速改变参数，并立刻得到相应的结果，该方法的优点是简单、快速、直观，对于初学者来说更容易掌握。

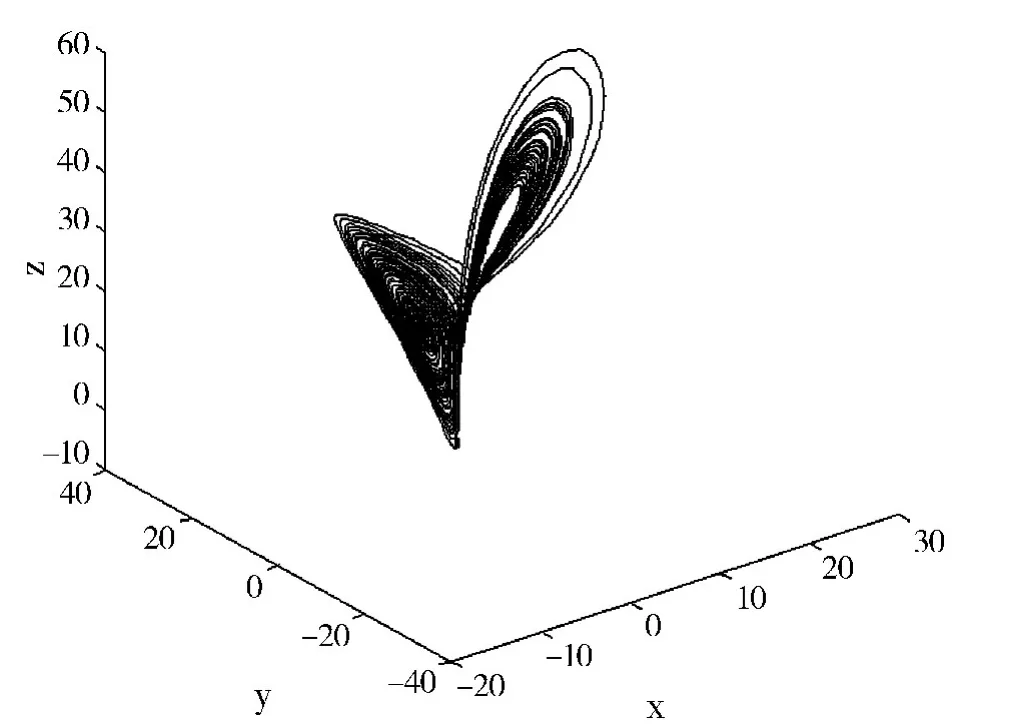
图3 Lorenz混沌吸引子三维相图

(五)引入科学前沿问题，开拓学生视野。随着科学技术的发展，长期不变的实验教学已不能满足教学需要，所以应将新的科研成果融入教学中，让学生掌握科学前沿知识，这样可以丰富教学内容，开拓学生视野，活跃学生思想，培养创新意识，从而提高教学质量。

本章内容其中一个重要的应用就是混沌系统的求解。混沌是非线性动力学系统中特有的一种运动形式，广泛存在于自然界，如生物学、物理、化学、电子学、信息学科以及技术科学、社会科学等各种领域。混沌是学者们研究的学术前沿问题之一。其中研究的最为深入的是Lorenz系统，其状态方程为:

式中 a=10，b=30，c=8/3，给定初始条件为 x(0)=0，y(0)=ε，z(0)=0，其三维相图见图3。给初始值一个微小扰动，然后求解观察，会发现两次计算结果完全不同，这就是混沌系统对初始条件的高度敏感性(失之毫厘，差之千里)，称之为蝴蝶效应。

Lorenz方程是没有解析解的，如果要手工绘出其图形很困难，但是用Matlab仿真，其效果和直观性是非常好的，便于学生理解与掌握。

另外，在绘制洛伦兹系统的相图时，可以固定参数a，c，令b从0到30变化，进一步观察相图，初步引入分岔的概念，如此有利于激发学生的求知欲，为日后的进一步研究奠定基础。

二、结语

对于常微分方程数值解的讲授，首先提出实际案例，让学生带着问题而入，激发学生求知欲;然后介绍算法，理论与实践相结合;再用Matlab仿真，主要介绍两种方法(龙格库塔法以及Simulink仿真)求解，结果表明:两种方法各有优点，前者帮助学生理解算法理论;后者从繁琐的算法中解脱出来，简单、直观，只需要画出模块连接图就可得到结果;最后引入科学前沿问题——混沌系统的求解，开拓了学生的视野，提高了学生兴趣，培养了创新意识，使教学质量上了一个新台阶。

［1］艾冬梅，李艳晴，张丽静等．MATLAB与数学实验［M］．北京:机械工业出版社，2010

［2］杨韧，谢海英，杨光崇．注重能力培养的数学实验课程建设探索［J］．大学数学，2013，29(3):9 ～11

［3］陈慧．数学实验课程教学改革研究［J］．中国大学数学，2007，12:35 ～36

［4］杨夷梅，杨玉军．Matlab教学中的方法与实践［J］．中国电力教育，2008，127:59 ～60

［5］韦程东，高扬，陈志强．在常微分方程教学中融入数学建模思想的探索与实践［J］．数学的实践与认识，2008，38(20):228～233

［6］刘钦圣，张晓丹，王兵团．数值计算方法教程［M］．北京:冶金工业出版社，1998