灰色犹豫模糊集及其灰关联TOPSIS决策方法
李庆胜,刘思峰
(1.南京航空航天大学经济与管理学院,江苏南京211106)
(2.临沂大学商学院,山东临沂276005)
灰色犹豫模糊集及其灰关联TOPSIS决策方法
李庆胜1,2,刘思峰1
(1.南京航空航天大学经济与管理学院,江苏南京211106)
(2.临沂大学商学院,山东临沂276005)
犹豫模糊集作为模糊集的最新扩展形式,在处理部分确定、部分不确定新方面有其独特的优势.在现实的犹豫模糊决策中,决策信息往往呈现部分信息已知,部分信息未知的特征,体现为灰信息的形式.基于此,文中提出了一种新的灰色犹豫模糊集合(gray hesitant fuzzy set,GHFS),将犹豫模糊集扩展到灰集领域.文章还给出了灰犹豫模糊元的距离计算公式,提出了GHFS的灰关联加权和TOPSIS(technique for order preference by similarity to an ideal solution)决策方法.专业市场发展策略的算例表明了方法的有效性与实用性.
灰色犹豫模糊集;灰关联;TOPSIS
自从文献[1]中提出模糊集以来,模糊集理论现已成功地应用于各个领域.由于客观世界的复杂性和不确定性,加上人们思维能力和知识水平的局限性,用于表达决策信息的形式不仅仅只是确定数,而经常以区间数的形式进行描述.由于传统的模糊集不能完整地刻画所研究问题的信息,文献[2-3]中引入了直觉模糊集并拓展到区间直觉模糊.由于直觉模糊集同时考虑了隶属度、非隶属度和犹豫度3个方面的信息,因此它广泛地应用于处理模糊性和不确定性等方面的问题.人们发现在进行群决策时,决策者们经常是犹豫和优柔寡断的,并且由于不能说服对方,使最终的决策结果难以达成一致.于是,文献[4-5]中提出了模糊集的另一种广义形式,即犹豫模糊集,其隶属度是由若干种可能的值构成的集合.
犹豫模糊集作为模糊集的最新扩展形式,有其独特的优势,因此引起了众多学者的研究兴趣.文献[6-7]中将犹豫模糊集推广至区间的形式,给出了区间犹豫模糊集的概念.
一个多属性决策问题往往同时包含模糊性和灰性,称之为灰色模糊多属性决策问题.文献[8]中提出了灰色模糊集合,认为这既是模糊集合的推广又是灰色集合的推广,是灰色集合与模糊集合的有机结合.文献[9]中认为灰色模糊多属性决策方法的研究己引起了人们的极大关注,但是灰色模糊多属性决策无论是在理论研究方面还是在方法应用方面,都还很不成熟,有待于人们的不断探索.
同时,一些学者把犹豫模糊集合和其他不确定性理论进行了有机的结合,进而提出了相关的多属性决策方法.文献[10]中提出了基于粗糙集的犹豫模糊多属性决策方法;文献[11]中提出了基于犹豫直觉模糊数的多属性决策方法.
在现实决策中,犹豫模糊决策权据往往是灰数的大概范围而不是其确切值,并非是在给定范围之内任意数皆可的区间数,因此文中提出灰色犹豫模糊集合,并进一步探讨基于灰关联加权的决策方法.为方便起见,文中采用多目标决策分析中的优劣解距离法(technique for order preference by similarity to an ideal solution,TOPSIS).TOPSIS法是根据有限个评价对象与理想化目标的接近程度进行排序的方法,在现有的对象中进行相对优劣的评价.
1 灰色犹豫模糊集
定义1[4-5]令X为一个给定的集合.形如A={〈x,hA(x)〉|x∈X}的二元组称为X上的犹豫模糊集.其中,hA(x)是由区间[0,1]上若干个不同的数构成的集合,表示元素x属于集合A的若干种可能隶属度构成的集合.为了书写方便,记hA(x)为犹豫模糊元.假如其每个犹豫模糊元中的元素只有一个,则犹豫模糊集退化为模糊集.
由于客观世界的复杂性和不确定性,以及人们思维能力和知识水平的局限性,人们经常以区间数的形式表达决策信息.因此,文献[6-7]中在犹豫模糊集的基础上,引入了区间犹豫模糊集.
定义2令X为一给定的集合,D[0,1]表示区间[0,1]上的所有闭子区间构成的集合.X上形如~A={〈x,~h~A(x)〉|x∈X}的二元组称为一个区间犹豫模糊集.其中~h~A(x):X→D[0,1]表示元素x属于集合~A的所有可能区间隶属度构成的集合.称~h~A(x)为一个区间犹豫模糊元.显然,对于一个区间犹豫模糊集,若其每个区间犹豫模糊元中的元素只有一个,则区间犹豫模糊集退化为区间模糊集;若其区间犹豫模糊元中的每个元素都为实数,则区间犹豫模糊集退化为犹豫模糊集.
只知道大概范围而不知道其确切值的数称为灰数.在应用中,灰数实际上指在某一个区间或某一个一般的数集内取值的不确定数;而区间数往往是指在区间范围之内的任意数.因此用灰数代替区间数,提出犹豫模糊集具有特定学术价值.
定义3令X为一给定的集合,g0[0,1]表示区间[0,1]上的所有闭子区间构成的集合.X上形如GA={〈x,ghA(x)〉|x∈X}的二元组称为一个灰色犹豫模糊集(GHFS).其中ghA(x):X→g0[0,1]表示元素x属于集合GA的所有可能灰色隶属度构成的集合,称ghA(x)为一个灰色犹豫模糊元.显然,对于一个灰色犹豫模糊集,若其每个灰色犹豫模糊元中的元素只有一个,则灰色犹豫模糊集退化为灰色模糊集;若其灰色犹豫模糊元中的每个元素都为实数,则灰色犹豫模糊集退化为犹豫模糊集.
显然灰色犹豫模糊集即是对犹豫模糊集的扩展,更属于灰集的一个特殊分支.这样可以进一步利用灰色系统的理论解决模糊数学所难以解决的小样本、贫信息以及不确定性问题[12],实现少数据建模.
定义4两个灰色犹豫模糊元gh1和gh2,它们之间的距离d(gh1,gh2)应该满足以下特性:
(1)0≤d(gh1,gh2)≤1.
(2)d(gh1,gh2)=0,当且仅当gh1=gh2时成立.
(3)d(gh1,gh2)=d(gh2,gh1).
在许多情况下,灰色犹豫模糊集中元素的个数是不等的,并且数值是处于无序状态.为了方便,假定l=max{lgh1,lgh2},其中l为灰色犹豫模糊集中元素的个数.为了更精确地计算两个灰色犹豫模糊元之间的距离,需要它们具有相同的个数,参考文献[13]制定了如下扩展规则:
定义5假定GA:gh={ghσ(i)|i=1,2,…,l},规定gh+和gh-分别为GHFE中的最大和最小值.称gh=ηgh++(1-η)gh-为扩展值.参数η(0≤η≤1)由决策者的风险偏好决定.当决策者是风险中性时,取η=0.5,此时扩展值gh=0.5(gh++ gh-);当决策者为风险规避者时,取η=0,此时扩展值gh=gh-;当决策者为风险寻求者时,取η=1,此时扩展值gh=gh+.
根据欧氏距离同时参考文献[13],给出GHFE的距离测度:
d(gh1,gh2)=

2 灰色关联TOPSIS决策方法
2.1 问题描述
在灰色犹豫模糊多属性决策时,根据各属性的评估值建立决策矩阵.设m个评价对象组成方案集A={A1,A2…Am},n个决策属性组成指标集X= {x1,x2,…xn},则灰色犹豫模糊决策矩阵GH为:

2.2 用灰色关联计算权重
目前已有不少研究成果研究群决策专家权重的确定,包括关联加权几何平均法、离差最大化法[14-16]等,这些方法从多方面、多角度解决了群决策中专家权重的确定问题.
灰色系统理论在处理小样本、贫信息,以及不确定问题上存在巨大优势,在多属性决策研究中得到广泛应用[12,17-18].文中依据文献[12]中提出的利用灰色关联确定群决策中指标权重的原理,将该原理扩展到灰色犹豫模糊集中.
定义6 GH0=(gh0(1),gh0(2),…gh0(n))

(1)计算灰色关联系数及灰色关联度[17-18]
首先利用公式(1),分别求出 GH0和 GH1,GH2,…,GHm的距离D,然后利用式(4)和式(5)求出灰色关联系数ζ(j)和灰色关联度γ(j),令D= d(ghi(j),gh0(j))


式中:ρ为分辨系数,ρ∈(0,1),一般取ρ=0.5各个数列的关联度大小,直接反映了各个评价指标相对于设定指标数列相对重要的程度,即权重大小.
(2)确定为各个决策指标的权重值wj.W(X)=(w1,w2,…wn)
式中:

2.3 确定正理想方案和负理想方案
在确定完属性权重后,把 TOPSIS决策方法[19-22]扩展到灰色犹豫模糊集,进行方案排序.正理想点PIS用GA+表示;负理想点NIS用GA-表示.
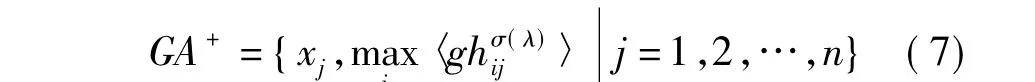
负理想方案:

2.4 计算第i方案到正负理想点的加权距离
在TOPSIS决策的实践中,各指标的重要程度不同,常常需要考虑权重因素.文中采用有关联加权距离的方法.各方案到正理想点的加权距离为:

各方案到负理想点的加权距离为:
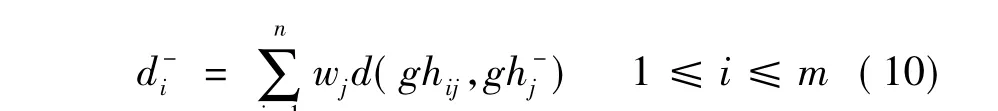
式中,wj为第j个指标的权重.
2.5 计算各方案的相对贴近度
各方案的相对贴近度ci的计算方法为

显然,相对贴近度越大,方案越优.基于以上分析,灰色犹豫模糊集的灰关联TOPSIS决策方法的主要步骤为①利用公式(4)、(5)和(6)得到属性权重向量;②利用公式(7)和(8)确定灰色犹豫模糊的正理想值GA+和负理想值GA-;③利用公式(9)和(10)计算方案Ai的d+i和d-i;④ 利用公式(11),计算各方案相对贴近度ci;⑤根据相对贴近度,选择最佳方案.
3 算例
专业批发市场可持续性发展决策受多种因素影响.正确的专业市场发展决策影响经济与社会各个方面.假定有5种备选发展方案Ai(i=1,2,3,4,5),有4种属性:P1为技术;P2为环境;P3为社会政治;P4为经济.邀请5位专家来评估5种方案.属性值以GHFS的形式给出,灰色犹豫模糊决策矩阵见表1.显然本例中属性值的长度不同,此处假定决策者为风险规避者,因此取η=0,扩展值gh= gh-,具体数值见表2.

表1 灰色犹豫模糊决策矩阵Table 1 Grey hesitation fuzzy decision-making matrix

表2 基于风险规避的灰色犹豫模糊扩充决策矩阵Table 2 Grey hesitation fuzzy decision-making extended matrix based on risk aversion
步骤1:利用式(4)、(5)得到灰色关联系数ζi(j)和灰色关联度γ(j),利用公式(6)得到w.

步骤2:利用公式(7)和(8)确定灰色犹豫模糊的正理想值GA+和负理想值GA
GA-=
{〈[0.2,0.5],[0.2,0.3],[0.2,0.3],[0.2,0.3],[0.1,0.3]〉,
〈[0.6,0.7],[0.3,0.4],[0.1,0.2],[0.1,0.2],[0.1,0.2]〉,
〈[0.3,0.5],[0.1,0.3],[0.1,0.2],[0.1,0.3],[0.1,0.2]〉,
〈[0.5,0.6],[0.3,0.4],[0.2,0.3],[0.2,0.3],[0.2,0.3]〉}
GA+=
{〈[0.7,0.9],[0.6,0.7],[0.5,0.6],[0.5,0.6],[0.5,0.6]〉,
〈[0.7,0.9],[0.7,0.8],[0.6,0.7],[0.5,0.6],[0.5,0.6]〉,
〈[0.7,0.9],[0.7,0.8],[0.6,0.7],[0.6,0.7],[0.6,0.7]〉,
〈[0.8,0.9],[0.7,0.8],[0.5,0.6],[0.5,0.6],[0.5,0.6]〉}
步骤3:利用公式(9)和(10)计算方案Ai(i=
步骤4:利用公式(11),计算各方案相对贴近度ci(i=1,2,3,4,5):
c1=0.3518,c2=0.3308,c3=0.5558,
c4=0.3404,c5=0.6803.
步骤5:根据相对贴近度,选择最佳方案ci(i= 1,2,3,4,5),对备选方案进行排序Ai(i=1,2,3,4,5)
显然,A5≻A3≻A4≻A1≻A2,这样最佳选择方案为A5.
4 结论
多属性决策问题往往面临着复杂的环境,并且可能会出现非精确的数据,甚至伴有模糊性和灰性.在现实决策中,犹豫模糊决策信息往往是只知道大概范围而不知道其确切值的灰权,而并非在给定范围之内任意数皆可的内涵,因此文中提出了用灰数代替区间数的灰色犹豫模糊集.它既是对犹豫模糊的扩展,更是对灰色系统的新应用领域的拓展.以此为基础,文中进一步提出了灰关联定权的TOPSIS决策方法,并用专业批发市场可持续性发展策略的算例证明了该方法的有效性和应用性.该方法可以在类似的经济与管理的决策中推广应用.
References)
[1] 扎德.模糊集[J].信息与控制,1995,8(3):338-356.Zadeh L A.Fuzzy sets[J].Information and Control,1995,8(3):338-356.(in Chinese)
[2]Atanssov K.Intutionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.
[3]Atanassov K,Gargov G.Intervalvalued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1989,31(3): 343-349.
[4]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.
[5]Torra V,Narukawa Y.On hesitant fuzzy sets and decision[C]∥The 18th IEEE International Conference on Fuzzy Systems.Jeju Island,Korea:[s.n.],2009: 1378-1382.
[6]Chen N,Xu Z S,Xia M M.Interval-valued hesitant preference relations and their applications to group decision making[J].Knowledge-Based Systems,2013,37 (2),528-540.
[7]Chen N,Xu Z S,Xia M M.Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis[J].Applied Mathematical Modelling,2013,37(4):2197-2211.
[8] 陈大为.灰色模糊集合[J].黑龙江水专学报,2000,27(4):103-108.
[9] 卢英.灰色模糊多属性决策分析方法研究[D].杭州:浙江工商大学,2009:3-15
[10] 朱丽,朱传喜,张小芝.基于粗糙集的犹豫模糊多属性决策方法[J].控制与决策,2014,29(7):1335-1339 Zhu Li,Zhu Chuanxi,Zhang Xiaozhi.Method for hesitant fuzzy multi-attribute decision making based on rough sets[J].Control and Decision,2014,29(7): 1335-1339.(in Chinese)
[11] 付超,赵敬.基于犹豫直觉模糊数的多属性决策方法[J].系统工程,2014,32(4):131-136.Fu Chao,Zhao Jing.Multiple attribute decision making method based on hesitation institution fuzzy number[J].Systems Engineering,2014,32(4):131-136.(in Chinese)
[12] 刘思峰,方志耕,谢乃明.基于核和灰度的区间灰数运算法则[J].系统工程与电子技术,2010,32(2): 313-316 Liu Sifeng,Fang Zhigeng,Xie Naiming.Algorithm rules of interval grey numbers based on the Kernel and the degree of greyness of grey numbers[J].Systems Engineering and Electronics,2010,32(2):313-316.(in Chinese)
[13]Xu Zeshui,Zhang Xiaolu Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information[J].Knowledge-Based Systems,2013,52(5):53-64.
[14]Xu Zeshui.A deviation-based approach to intuitionistic fuzzy multiple attribute group decision making[J].Group Decision and Negotiation,2010,19(1):57-76.
[15]Xu Zeshui.Deviation measures of linguistic preference relations in group decision making[J].Omega,2005,33(3):249-254.
[16]Wu Zhibin,Chen Yihua.The maximizing deviation method for group multiple attribute decision making under linguistic environment[J].Fuzzy Sets and Systems,2007,158(14):1608-1617.
[17] 王正新,党耀国,曹明霞.基于灰熵优化的加权灰色关联度[J].系统工程与电子技术,2010,32(4): 119-122.Wang Zhengxin,Dang Yaoguo.Cao Minxia.Weighted grey relational degree based on grey entropy optimization[J].System Engineering and Electronic Technology,2010,32(4):119-122.(in Chinese)
[18]Sun Jiaqi.Combining grey relation analysis and entropy model for evaluating the operational performance:an empirical study[J].Quality&Quantity,2014,48(3): 109-113. [19]余雁,梁樑.多指标决策TOPSIS方法的进一步探讨[J].系统工程,2003,21(2):98-101.Yu Yan,Liang Liang.Extensions of the TOPSIS for multiple criteria decision making[J].System Engineering,2003,21(2):98-101.(in Chinese)
[20]徐泽水.一种基于目标贴近度的多目标决策方法[J].系统工程理论与实践,2001,21(9):101-103 Xu Zeshui.A method based on objective similarity scale for multi-objective decision-making[J].System Engineering Theory and Practical,2001,21(9):101-103.(in Chinese)
[21]Yue Zhongliang.An extended TOPSIS for determining weights of decision makers with interval numbers[J].Knowledge Based Systems,2011,24(1):146-153.
[22] 王砚羽,张卓,王正新.基于灰色关联系数改进的加权TOPSIS法及其应用[J].华东经济管理,2011,25 (10):139-144.Wang Yanyu,Zhang Zhuo,Wang Zhengxin.An improved weighted topsis method and its application based on grey relational coefficient[J].East China E-conomic Management,2011,25(10):139-144.(in Chinese)
(责任编辑:童天添)
Grey hesitant fuzzy sets and its decision making based on grey relation and TOPSIS
Li Qingsheng1,2,Liu Sifeng1
(1.School of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing Jiangsu 211106,China)
(2.School of Business,Linyi University,Linyi Shandong 276005,China)
As a fuzzy set of the latest extension form,hesitant fuzzy set has its unique advantage in dealing with the data of partial certainty and partial uncertainty.In reality,in the hesitant fuzzy decision-making,the information is often partially known and partially unknown,embodied in the form of grey information.So we propose a new grey hesitant fuzzy set(GHFS)which is an extension to grey sets of the hesitant fuzzy set.This paper also presents the calculation formula of grey hesitant fuzzy element distance,and then puts forward the grey weighted and TOPSIS decision method of GHFS.A professional market development strategy selection problem is used to illustrate the detailed implementation process of the proposed approach and to demonstrate its validity and applicability.
grey hesitant fuzzy set;grey relation; TOPSIS
C934
A
1673-4807(2015)06-0597-05
10.3969/j.issn.1673-4807.2015.06.016
2015-09-09
国家自然科学基金国际(地区)合作与交流项目(71111130211);国家自然科学基金资助项目(70901041,70701017);国家自然科学基金重大研究计划培育项目(90924022);国家自然科学基金资助项目(70971064)
李庆胜(1970—),男,博士研究生,研究方向为灰色系统、不确定性决策.E-mail:liqingshengguanli@163.com
李庆胜,刘思峰.灰色犹豫模糊集及其灰关联Topsis决策方法[J].江苏科技大学学报(自然科学版),2015,29(6):597-601.

