一种新的广义多粒度优势关系粗糙集
张 明,孙佳伟,程 科,徐维艳,潘 磊
(1.江苏科技大学计算机科学与工程学院,江苏镇江212003)
(2.江苏科技大学数理学院,江苏镇江212003)
一种新的广义多粒度优势关系粗糙集
张 明1,孙佳伟1,程 科1,徐维艳2,潘 磊1
(1.江苏科技大学计算机科学与工程学院,江苏镇江212003)
(2.江苏科技大学数理学院,江苏镇江212003)
通过分析乐观和悲观多粒度优势关系粗糙集下近似的决策过程,提出了一种新的广义多粒度优势关系粗糙集,并将乐观多粒度优势关系粗糙集和悲观多粒度优势关系粗糙集统一到广义多粒度优势粗糙集模型中.然后,比较了这3种多粒度优势关系粗糙集的下近似、上近似和度量因子之间的关系.最后讨论了广义多粒度优势关系粗糙集的一些基本性质.
粗糙集;多粒度;优势关系
多粒度化的粗糙集数据建模方法是近年来快速兴起的一种多视角数据分析方法,在文献[1-3]中首先被提出,用于克服Pawlak粗糙集的缺陷,如:①进行面向多源信息系统的知识发现时算法耗时过多;②处理具有高维特征的数据时低效;③在处理分布式信息系统和多智能Agent时不适应性;等等.随后多粒度化的粗糙集数据建模思想得到了很多学者的关注[4-13].
经典的粗糙集数据分析方法没有考虑到所描述对象的属性常常具有顺序性的特征,如投资回报率、市场份额、负债率等,这些属性一般被称为准则.文献[14]中首先提出了一种基于优势关系的粗糙集模型,用于处理具有偏序性质的信息系统(序信息系统);文献[9-11]中将Greco的优势关系粗糙集模型推广到多粒度化的环境中,并研究了乐观多粒度优势关系粗糙集和悲观多粒度优势关系粗糙集模型.
然而,通过分析乐观和悲观多粒度优势关系粗糙集的数据分析方法可以发现:乐观多粒度优势关系粗糙集的下近似需要至少一个优势关系中存在优势类与目标概念保有包含关系,而悲观多粒度优势关系粗糙集的下近似需要所有优势关系存在优势类与目标概念保有包含关系.因此,在应用中面临这两种多粒度优势关系粗糙集模型的选择问题.为了便于多粒度优势关系粗糙集的应用和推广,文中提出一种新的多粒度优势关系粗糙集,将乐观和悲观多粒度优势关系粗糙集统一到广义多粒度优势关系粗糙集中,解决了多粒度优势关系粗糙集模型统一的问题.
1 基本概念
1.1 单粒度优势关系粗糙集
决策信息系统DIS可以定义为一个四元组: DIS=<U,C∪{d},V,f>,其中论域U是非空有限对象集;C是有限条件属性集,d是决策属性,且C∩{d}=∅;∀a∈C∪{d},Va表示属性a的值域;V是全体属性的值域,即V=VC∪Vd;f是信息函数,∀x∈U,a∈C∪{d},f(x,a)表示对象x在属性a上的取值.
如果属性集C∪{d}的取值具有偏好次序,则决策信息系统DIS=<U,C∪{d},V,f>又被称为序决策信息系统ODIS.在序决策信息系统中将这种具有偏好次序的属性(集)称为准则(集),这类问题又称为多准则决策问题.
在序决策信息系统ODIS中,若属性a存在一个偏序关系≥a,则x≥ay表示样本x在属性a上的取值优于y在a上的取值,即f(x,a)≥f(y,a).同理定义偏序关系≤a,则x≤ay表示x在属性a上的取值劣于y在a上的取值,即f(x,a)≤f(y,a).为了简化讨论并且不失一般性,文中仅讨论偏序关系≥a.
定义1设ODIS=<U,C∪{d},V,f>,∀A⊆C,定义A上的优势关系为:
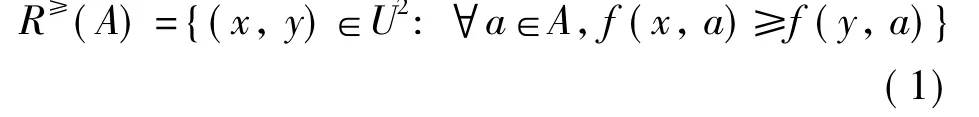
易知优势关系R≥(A)满足自反性和传递性,但不满足对称性.在序决策信息系统中,根据优势关系可以计算对象x的优势类R≥A(x),且R≥A(x)= {y∈U:(y,x)∈ R≥(A)},x的优势类表示在属性集(准则集)A上,所有取值优于x的对象集.优势关系还可以导出论域U上的一个划分U/R≥(A)= {R≥A(x1),R≥A(x2),…,R≥A(xn)}.
根据粒计算的观点[9,15],优势关系R≥(A)对应一个粒度(Granulation),由优势关系导出的划分U/R≥(A)对应一个粒结构或粒空间(Granulation Space),优势类R≥A(x)被称为知识(颗)粒(Knowledge Granule).
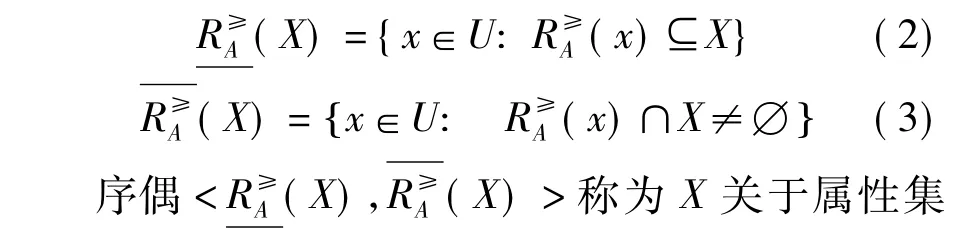
定义2设ODIS=<U, C∪{d},V,f>,∀X⊆U,A⊆C,定义X关于属性A的优势关系下、上近似分别为: A的优势关系粗糙集.易知优势关系粗糙集是通过单个优势关系中的知识粒,以下、上近似的形式来表示未知目标,因此经典的优势关系粗糙集是单粒度(化)优势关系粗糙集.
1.2 多粒度优势关系粗糙集
文献[9-11]中引入多粒度化粗糙集数据分析思想,结合Greco的单粒度优势关系粗糙集理论,处理多准则决策问题,并形成乐观多粒度优势关系粗糙集和悲观多粒度优势关系粗糙集两种数据分析方法.
1.2.1 乐观多粒度优势关系粗糙集
定义3设ODIS=<U,C∪{d},V,f>,A1,A2,…,Am是C的m个属性子集(m≤2|C|),对应优势关系R≥(A1),R≥(A2),…,R≥(Am).对任意X⊆U,定义X关于属性子集A1,A2,…,Am的乐观多粒度优势关系粗糙集的下、上近似分别为:关于属性A1,A2,…,Am的乐观多粒度优势关系粗糙集.
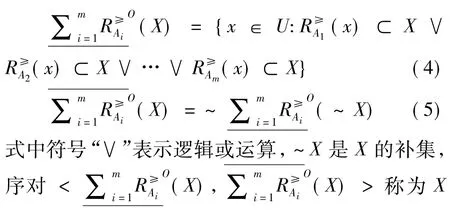
文献[9]中通过定义乐观多粒度优势关系粗糙集的不确定性因子、精确近似度因子和依赖度因子来度量乐观多粒度优势关系粗糙集,具体定义如下:
定义4设ODIS=<U,C∪{d},V,f>,A1,A2,…,Am是C的m个属性子集,对任意X⊆U (X≠∅),X的关于属性集A1,A2,…,Am的乐观多粒度优势关系粗糙集的不确定性因子和精确近似度因子的定义为:
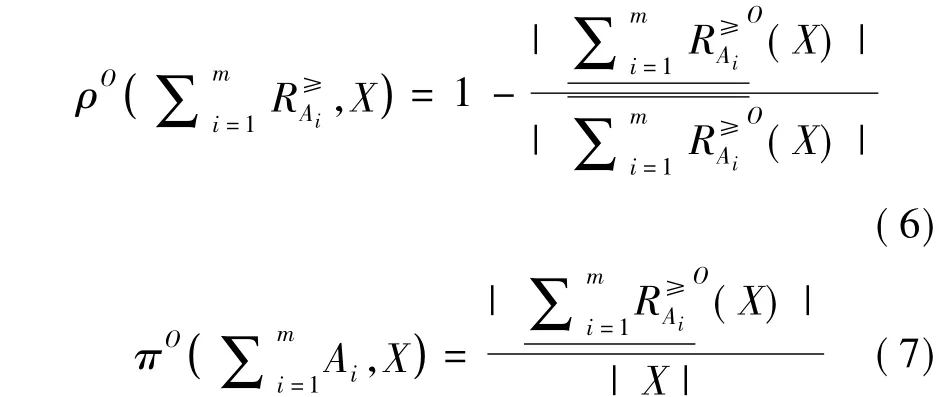
定义5设ODIS=<U, C∪{d},V,f>,A1,A2,…,Am是C的m个属性子集,若D=U/d ={D1,D2,…,Dr}由决策属性d在论域U上导出的划分,则D对属性集A1,A2,…,Am的乐观多粒度优势关系粗糙集的依赖程度的定义为:
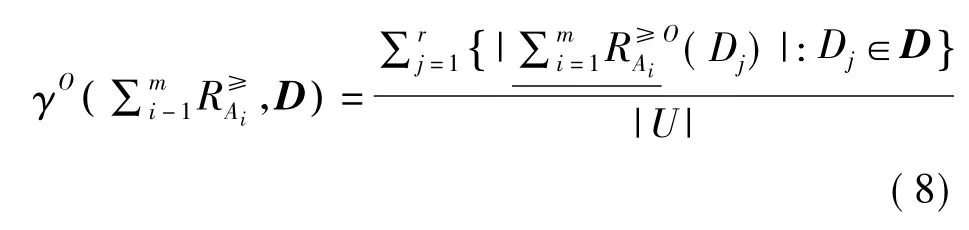
1.2.2 悲观多粒度优势关系粗糙集
定义6设ODIS=<U,C∪{d},V,f>,A1,A2,…,Am是C的m个属性子集(m≤2|C|),对应优势关系R≥(A1),R≥(A2),…,R≥(Am).对任意X⊆U,定义X关于属性子集A1,A2,…,Am的悲观多粒度优势关系粗糙集的下、上近似,分别记为:
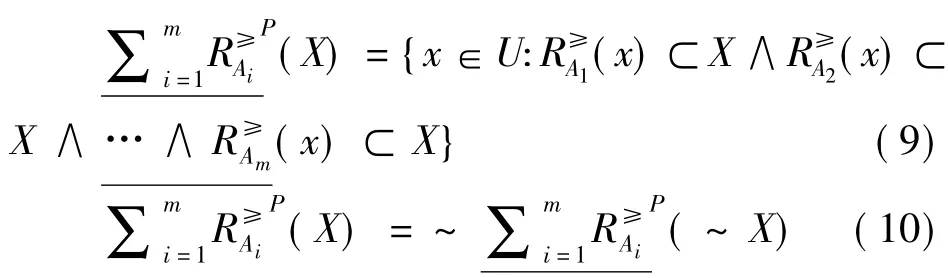
定义7设ODIS=<U,C∪{d},V,f>,A1,A2,…,Am是C的m个属性子集,对任意X⊆U(X≠∅),X的关于属性子集A1,A2,…,Am的悲观多粒度优势关系不确定性因子和精确近似度因子的定义为:
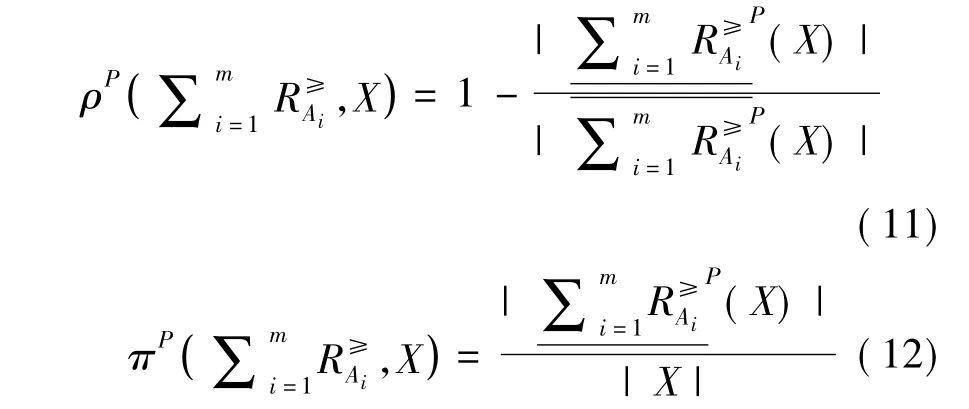
定义8设ODIS=<U,C∪{d},V,f>,A1,A2,…,Am是C的m个属性子集,若D=U/d= {D1,D2,…,Dr}是由决策属性d在论域U上导出的划分,则D对属性子集A1,A2,…,Am的悲观多粒度优势关系粗糙集的依赖程度的定义为:
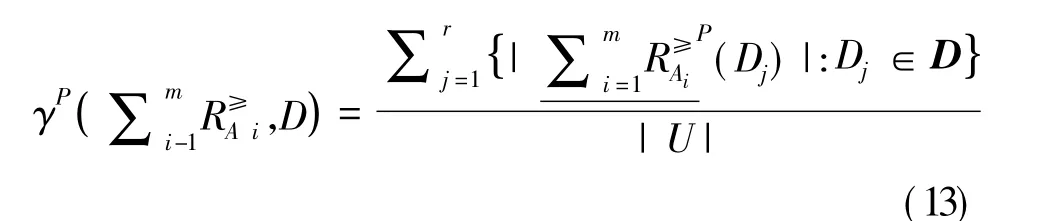
2 广义多粒度优势关系粗糙集
通过分析研究乐观和悲观多粒度优势关系粗糙集的下近似决策过程,可以发现:①乐观多粒度优势关系粗糙集的下近似需要至少一个优势关系存在优势类与目标概念保有包含关系;② 悲观多粒度优势关系粗糙集的下近似需要所有的优势关系存在优势类与目标概念保有包含关系.为了便于应用和推广多粒度优势关系粗糙集的数据分析方法,文中提出一种新的广义多粒度优势关系粗糙集,通过引入一个参数β来控制满足包含关系的优势关系的数目.当β变小时,广义多粒度优势关系粗糙集就趋向于乐观多粒度优势关系粗糙集;当β变大时,变粒度优势关系粗糙集就趋向于悲观多粒度优势关系粗糙集.根据处理实际问题的需要,通过动态设置β值可以使广义多粒度优势关系粗糙集具有乐观多粒度优势关系粗糙集和悲观多粒度优势关系粗糙集的特性.
定义9设ODIS=<U,C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集(m≤2|C|),对应优势关系 R≥(A1),R≥(A2),…,R≥(Am).令A={A1,A2,…,Am},对任意X⊆U,定义X关于A的广义多粒度优势关系的下、上近似为: X关于条件属性子集族A的广义多粒度优势关系粗糙集.
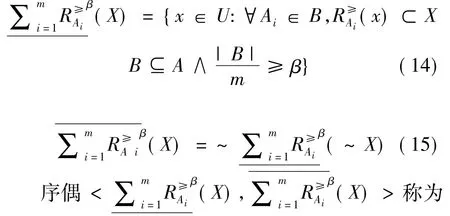
定义10设ODIS=<U,C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集.令A={A1,A2,…,Am},对任意X⊆U(X≠∅),X关于A的广义多粒度优势关系粗糙集的不确定性因子、精确近似程度因子分别定义为:
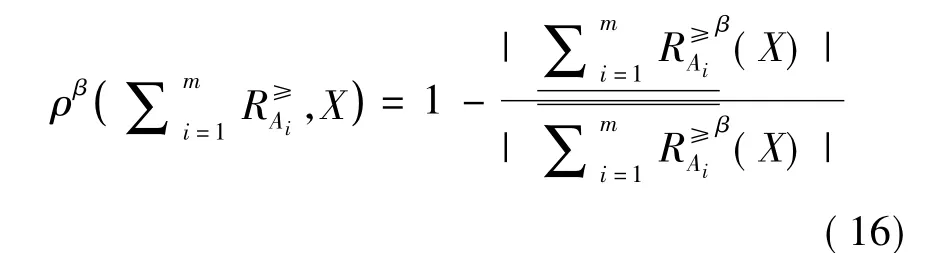
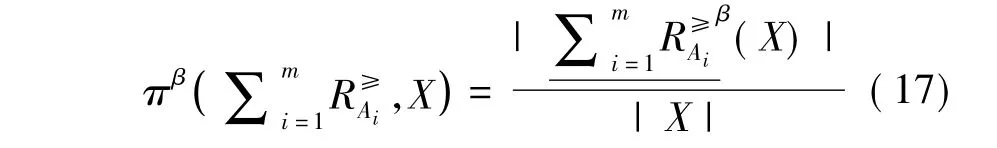
定义11设ODIS=<U, C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集,若A={A1,A2,…,Am},D=U/d={D1,D2,…,Dr}是由决策属性d在论域U上导出的划分,则D对属性子集族A的广义多粒度优势关系粗糙集的依赖程度为:
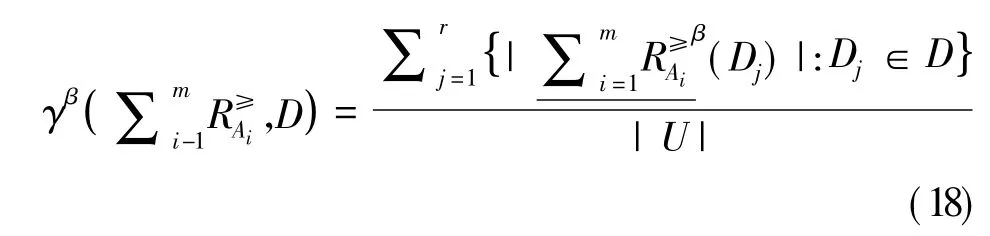
定理1设ODIS=<U,C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集.令A= {A1,A2,…,Am},∀X⊆U可得:
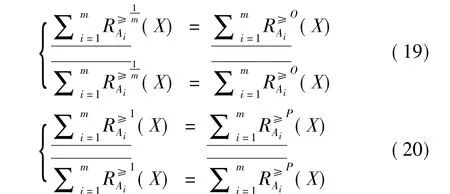
证明:由定义9和定义3可知:
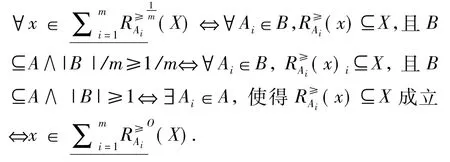
又由定义9和上面的结论可知:
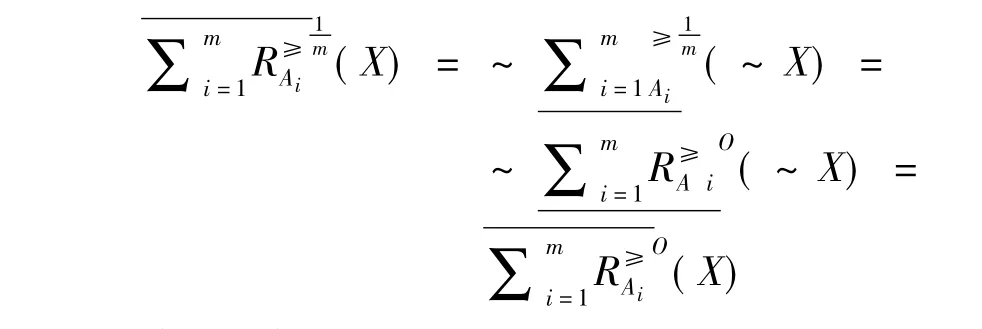
综上可知式(19)成立,同理可以证明式(20)也成立.
定理1表明:当β=1/m时,广义多粒度优势关系粗糙集就退化为乐观多粒度优势关系粗糙集;当β=1时,广义多粒度优势关系粗糙集就退化为悲观多粒度优势关系粗糙集.因此,广义多粒度优势关系粗糙集是乐观和悲观多粒度优势关系粗糙集的泛化,乐观和悲观多粒度优势关系粗糙集是广义多粒度优势关系粗糙集的两种特例.
定理2设ODIS=<U,C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集.令A={A1,A2,…,Am},则广义多粒度优势关系粗糙集与乐观和悲观多粒度优势关系粗糙集相比有如下的性质:
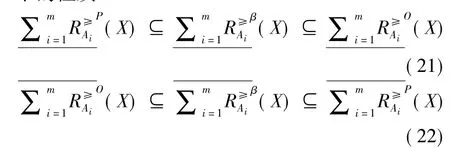
综上可知式(21)式成立.用类似方法可以证明式(22)也成立.
定理2表明:广义多粒度优势关系粗糙集的下近似大于或等于悲观多粒度优势关系粗糙集下近似,而小于或等于乐观多粒度优势关系粗糙集;广义多粒度优势关系粗糙集的上近似大于或等于乐观多粒度优势关系粗糙集上近似,而小于或等于悲观多粒度粗糙集的上近似.
定理3设ODIS=<U,C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集.令A= {A1,A2,…,Am},对任意X⊆U(X≠∅),X关于A的广义多粒度优势关系粗糙集、乐观和悲观多粒度优势关系粗糙集对应的不确定性因子、精确近似程因子和依赖度因子有如下的关系成立:
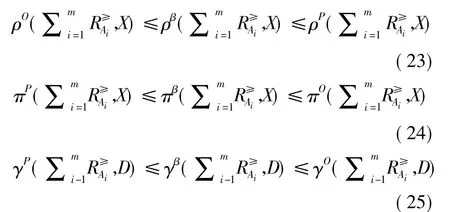
定理3表明:①广义多粒度优势关系粗糙集的不确定性因子大于或等于乐观多粒度优势关系粗糙集的不确定性因子,而小于或等于悲观多粒度优势关系粗糙集的不确定性因子;② 广义多粒度优势关系粗糙集的精确近似程因子和依赖度因子大于或等于悲观多粒度优势关系粗糙集的精确近似程因子和依赖度因子,而小于或等于乐观多粒度优势关系粗糙集的精确近似程因子和依赖度因子.
定理4设ODIS=<U,C∪{d},V,f>,0<β≤1,A1,A2,…,Am是C的m个属性子集.令A= {A1,A2,…,Am},则广义多粒度优势关系粗糙集有如下的性质:
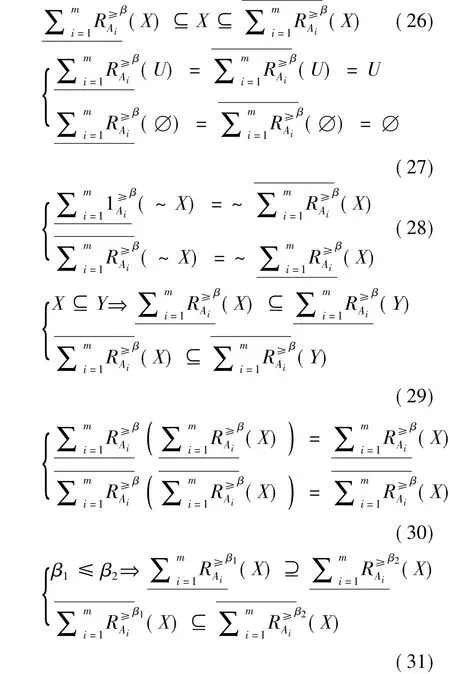
证明:
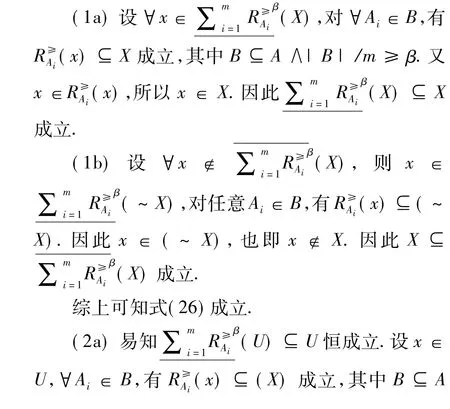

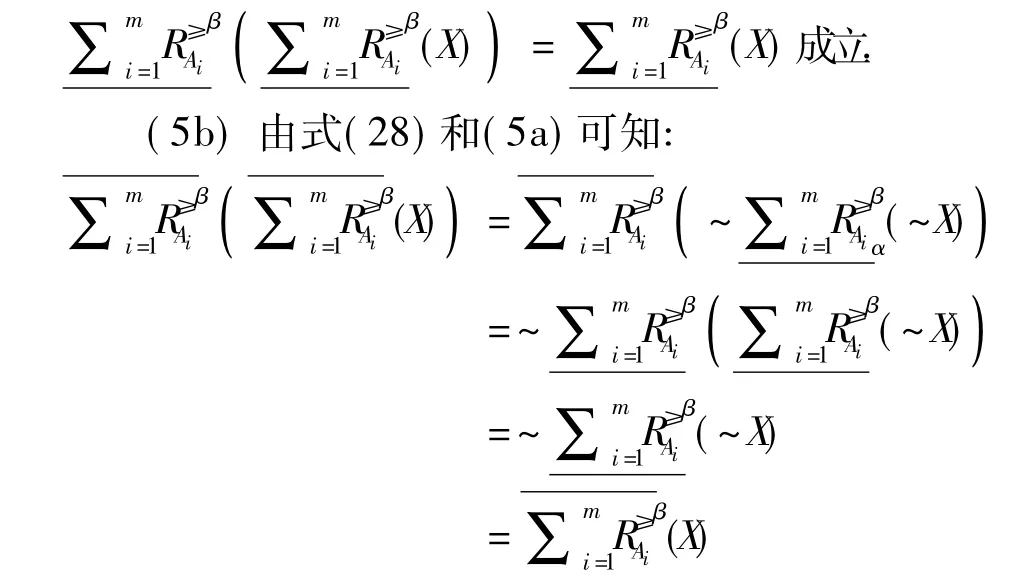
综上可知式(30)成立.
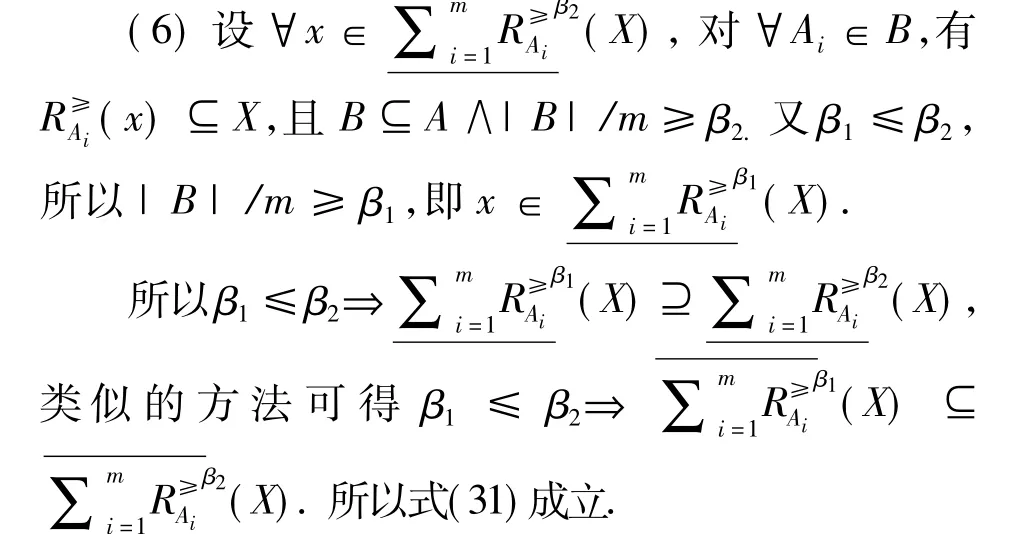
定理4给出的广义多粒度优势关系粗糙集基本性质表明:①广义多粒度优势关系粗糙集的下、上近似和目标概念之间是包含关系;② 广义多粒度优势关系粗糙集的下、上近似满足同一律;③广义多粒度优势关系粗糙集下、上近似之间满足互补律;④广义多粒度优势关系粗糙集下、上近似运算满足单调性;⑤广义多粒度优势关系粗糙集下、上近似运算满足幂等律;⑥ 广义多粒度优势关系粗糙集下、上近似运算关于β是单调的.
3 实例分析
表1是关于工程项目是否实施的序决策信息系统实例,论域U={x1,x2,x3,x4,x5,x6}表示需要决策的6个项目;条件属性集C={c1,c2,c3}表示3个不同专家以本领域的知识给出的评分(5分制,满分5分);d是决策属性,表示对应的项目是否通过专家的评审.
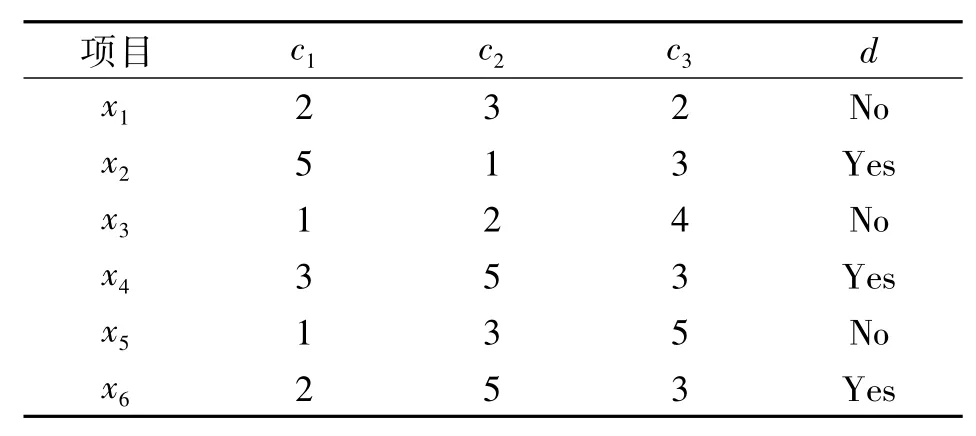
表1 序决策信息表Table 1 Order decision information table
令条件属性子集簇A={{A1},{A2},{A3}} ={{c1},{c2},{c3}},X={x2,x4,x6}为通过决策的项目,β=0.6.
由定义1可计算得到属性子集簇A对应的优势关系所导出的一个粒度结构:
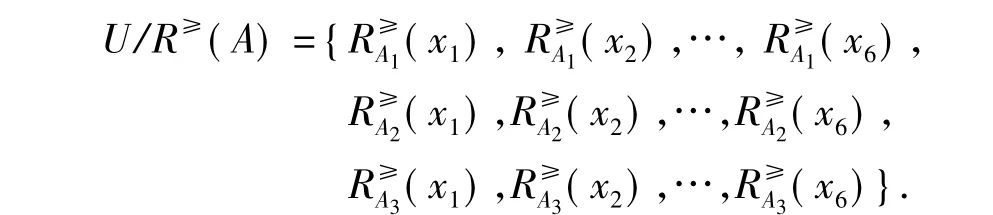
式中:
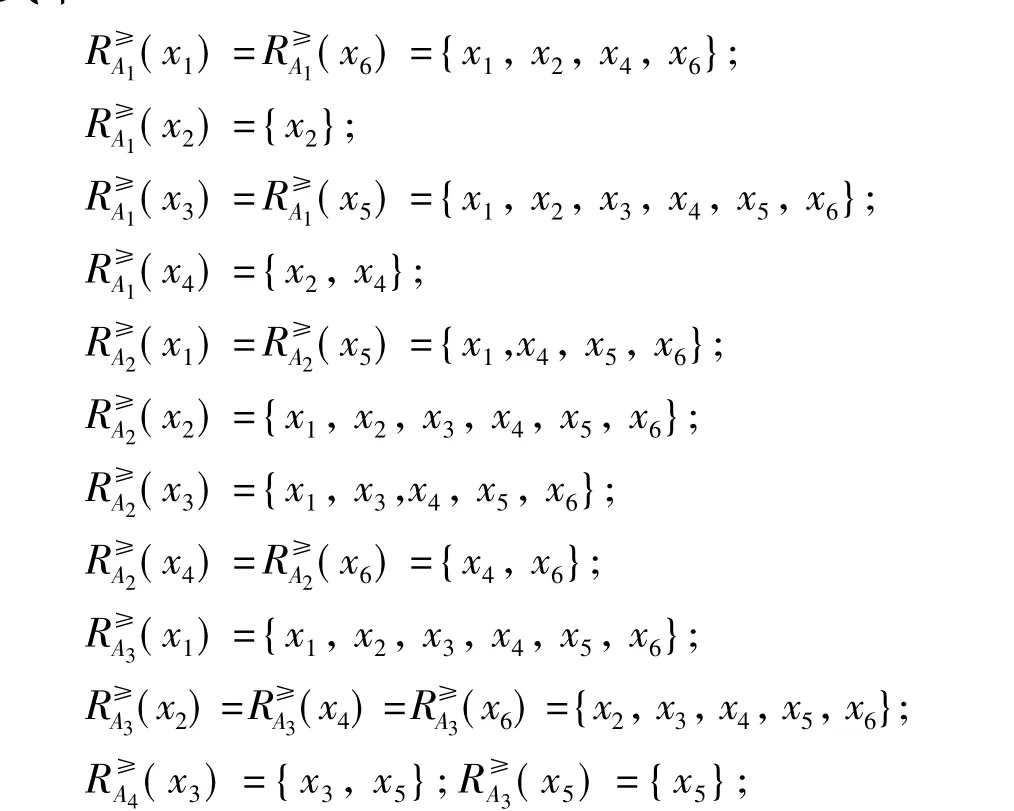
由定义3可知:
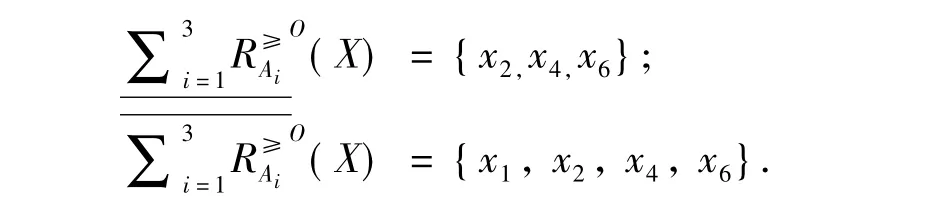
由定义6可知:
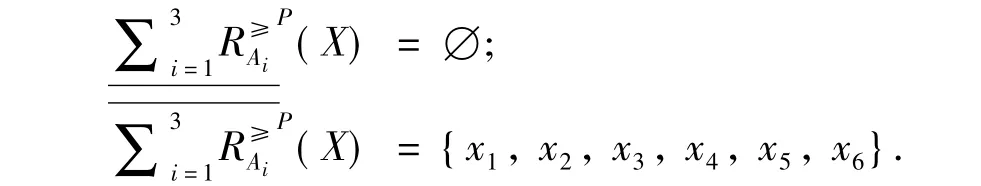
由定义9可知:
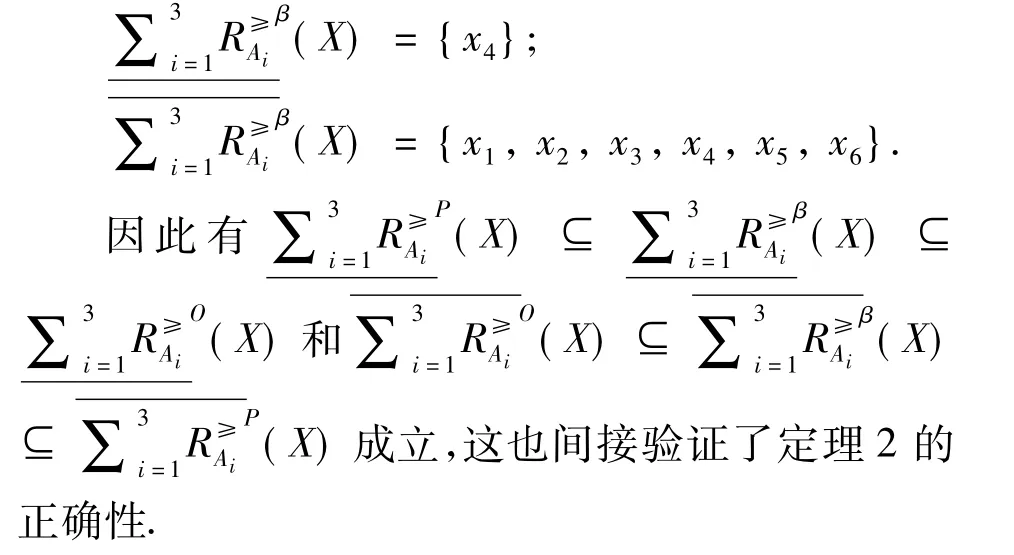
4 结论
多粒度化粗糙集数据分析方法是近年来涌现的一种新型数据建模方法,引起了很多学者的关注.文中通过深入分析乐观多粒度优势关系粗糙集和悲观多粒度优势关系粗糙集的决策机制,提出了一种广义多粒度优势关系粗糙集模型,解决了多粒度优势关系粗糙集在应用中模型统一的问题,下一步工作是进一步研究广义多粒度优势关系粗糙集在具体问题中的应用.
References)
[1]Qian Y H,Liang J Y,Yao Y Y,et al.MGRS:a multigranulation rough set[J].Information Sciences,2010,180(6):949-970.
[2]Qian Y H,Liang J Y,Dang C Y.Incomplete multigranulation rough set[J].IEEE Transactions on Systems,Man and Cybernetics,Part A,2010,40(2): 420-431.
[3] 桑妍丽,钱宇华.一种悲观多粒度粗糙集中的粒度约简算法[J].模式识别与人工智能,2012,25 (3):361-366.Sang Yanli,Qian Yuhua.A granular space reduction approach to pessimistic multi-granulation rough set[J].Pattern Recognition and Artificial Intelligence,2012,25(3):361-366.(in Chinese)
[4]Lin G P,Qian Y H,Li J J.NMGRS:neighborhoodbased multigranulation rough sets[J].International Journal of Approximate Reasoning,2012,53(7):1080 -1093.
[5]She Y H,He X L.On the structure of the multigranulation rough set model[J].Knowledge-Based Systems,2012,36:81-92.
[6]Yang X B,Zhang Y Q,Yang J Y.Local and global measurements of MGRS rules[J].International Journal of Computational Intelligence Systems,2012,5(6): 1010-1024.
[7]Qian Y H,Zhang H,Sang Y L,et al Y.Multigranulation decision-theoretic rough sets[J].International Journal of Approximate Reasoning,2014,55(1): 225-237.
[8] 刘财辉.一种元素最大描述下的多粒度覆盖粗糙集模型[J].计算机科学,2013,40(12):64-67.Liu Caihui.Covering-based multigranulation rough set model based on maximal description of elements[J].Computer Science,2013,40(12):64-67.(in Chinese)
[9]Xu W H,Sun W X,Zhang X Y,et al.Multiple granulation rough set approach to ordered information systems[J].International Journal of General Systems,2012,41(5):475-501.
[10] 翟永健,张宏.不完备信息系统中的优势关系多粒度粗糙集[J].南京理工大学学报,2012,36(1):66 -72.Zhai Yongjian,Zhang Hong.Dominance-based multigranulation rough sets in incomplete information system[J].Journal of Nanjing University of Science and Technology,2012,36(1):66-72.(in Chinese)
[11] 李气芳,李进金,林国平.优势关系下的多粒度粗糙集[J].计算机工程与应用,2012,48(17):53-57.Li Qifang,Li Jinjin,Lin Guoping.Multi-granulation rough set based on dominance relation[J].Computer Engineering and Applications,2012,48(17):53-57.(in Chinese)
[12]张明,唐振民,徐维艳,等.可变粒度粗糙集模型[J].模式识别与人工智能,2012,25(4):709-720.Zhang M,Tang Z M,Xu W Y,et al.Multigranulation rough set model[J].Pattern Recognition and Artificial Intelligence,2012,25(4):709-720.(in Chinese)
[13]Zhang M,Xu W Y,Yang X B,et al.Incomplete variable multigranulation rough sets decision[J].Applied Mathematics&Information Sciences,2014,8(3):1159 -1166.
[14]Greco S,Matarazzo B,Slowinski R.Rough approximation by dominance relations[J].International Journal of Intelligent Systems,2002,17(2):153-171.
[15]Yao Y Y.Information granulation and rough set approximation[J].International Journal of Intelligent Systems,2001,16(1):87-104.
(责任编辑:童天添)
A new generalized multigranulation rough set based on dominance relation
Zhang Ming1,Sun Jiawei1,Cheng Ke1,Xu Weiyan2,Pan Lei1
(1.School of Computer Science and Engineering,Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China)
(2.School of Mathematics and Physics,Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China)
On the base of the lower approximation sets,the decision-making process is analyzed by the optimism and pessimism multigranulation dominance-based rough sets.A new generalized multigranulation dominancebased rough set is put forward,and the rough sets model of the optimism and pessimism multigranulation dominance-based rough set will be unified to it.Then,the relationship of the lower approximation,the upper approximation and the measurement factors are compared among the generalized multigranulation dominance-based rough set,the optimism multigranulation rough set and pessimism multigranulation rough set.Finally some basic properties of the generalized multigranulation dominance-based rough set are discussed.
rough sets;multigranulation; dominance relation
TP18
A
1673-4807(2015)06-0560-07
10.3969/j.issn.1673-4807.2015.06.010
2015-05-26
国家自然科学基金资助项目(61100116);江苏省自然科学基金资助项目(BK2011492,BK20130472);江苏省科技支撑项目(BE2014692)
张明(1978—),男,博士后,副教授,研究方向为智能信息处理、粗糙集与粒计算等.E-mail:zm_fred@163.com
张明,孙佳伟,程科,等.一种新的广义多粒度优势关系粗糙集[J].江苏科技大学学报(自然科学版),2015,29(6):560-566.

