直流微网中高降压比软开关DC-DC变换器

赵晋斌，火彩玲，屈克庆，李 芬

(上海电力学院 电气工程学院，上海 200090)

目前，在全球能源短缺与环境危机双重压力下，分布式电源(DER)在直流微电网中的应用越来越广泛，[1-2]基于数据中心直流配电系统提出的380 V的直流微网(DCMG)已逐渐得到业界的认可.[3]由DER构成的 DCMG配电网结构简单，易于实现不间断供电，能更好地满足配电网的供电要求.[4-5]

为了提供不同电压等级的低压直流负载(如LED 灯)，可以采用级联型直流变换结构，[6-7]但其存在结构复杂、成本高和转换效率低的问题.[5]若采用单级变换拓扑可以较好地解决上述问题，但现有的DC-DC变换器难以实现较大的降压转换比.因此，研究具有高降压比特性的拓扑具有重要的现实意义.

通常，为了实现变换器的高降压特性，多采用单级隔离型和级联型DC-DC拓扑结构.文献[8]至文献[9]采用单级隔离型DC-DC变换器，通过改变变压器的变比实现了高降压，但过高的降压比将导致变压器漏感增大，不仅会引起占空比的丢失，不利于变流器的优化设计，而且会造成二次侧整流管出现电压尖峰、整流器件电压应力增大、变换器效率降低等问题.文献[10]至文献[13]采用级联型DC-DC拓扑结构，通过两级直流变换实现了高压转换，各级的输入、输出电压之差都小于单级直流变换器的输入、输出电压之差，能够减轻单级变换器所承受的负担，大大增强了低压负载供电的适应能力，但级联型DC-DC变换器的体积较大，控制复杂，在高降压比条件下难以实现较好的稳定性.

鉴于上述问题，本文提出一种具有高降压转换特性的DC-DC变换器，能很好地实现高降压比和软开关动作，且具有输出响应速度快、抗负载扰动强及电路稳定性好等优点.

1 高降压比软开关直流变换器

1.1 电路结构分析

本文提出的具有高降压比特性的DC-DC拓扑结构如图1所示.该拓扑结构包括两个开关S1和 S2，寄生电容Cs1和Cs2，电容C c，续流二极管D，中间电感L1和输出电感L2，滤波电容Co和负载电阻Ro.

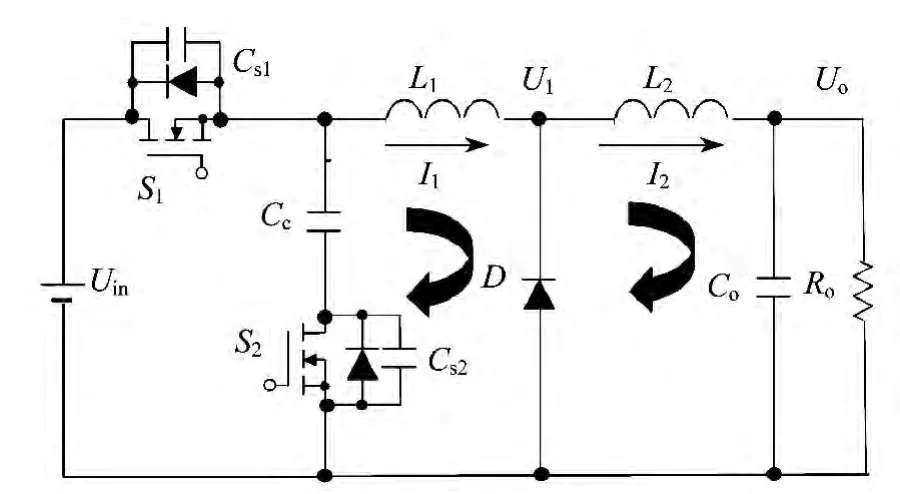
图1 高降压比软开关直流变换电路示意

1.2 电路工作原理分析

其电路的主要波形如图2所示.其中Ugs1和Ugs2分别为开关 S1和 S2的门极触发电压;Uds1和Uds2分别为开关S1和S2的端电压.I1和I2分别为流过电感L1和L2的电流;U1为二极管D端电压，Uo为输出电压;D为开关占空比，D'为仿真的实际占空比.在一个开关周期中共分6种模式(假设t0为初始时刻)，各等效模式如图3所示.

图2 电路的主要波形

模式1(t0～t1) 开关 S1导通，L1通过Uin充电，I1线性增加，同时，续流二极管正向偏置，L2通过Uo放电，I2线性减小.在t1时刻，电流I1过零变正，该模式结束.

模式2(t1～t2) 当充电电流I1与放电电流I2相等时，该模式结束.

模式3(t2～t3) 在I1=I2时，续流二极管反向偏置，L1和L2同时进入串联充电模式.当I1=I2=Imax时，该模式结束，得到如下方程:

解得:

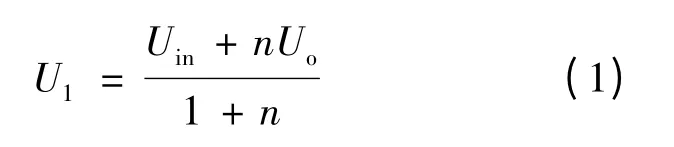
式中:n=L1/L2.

模式4(t3～t4) 开关 S1关断，I1正向放电，给开关的寄生电容Cs1充电，Cs2放电，电容Cc充电.当Cs2放电为零时，S2的寄生二极管导通，使Uds2=0，这给S2零电压导通创造了条件，L2通过Uo放电，I2线性减小.

模式5(t4～t5) 开关 S2零电压导通(实现软开关)，L1放电，I1线性减小;续流二极管正向偏置，L2通过Uo放电，I2线性减少，当I1=Imin时，该模式结束.

模式6(t5～t0) 电流I1反向放电，电容Cc放电，使开关寄生电容Cs2充电，Cs1放电.当Cs1放电为零时，开关S1的寄生二极管导通，使Uds1=0，这给S1零电压导通创造了条件，L2通过Uo放电，I2线性减小.该模式至t=t0时结束.

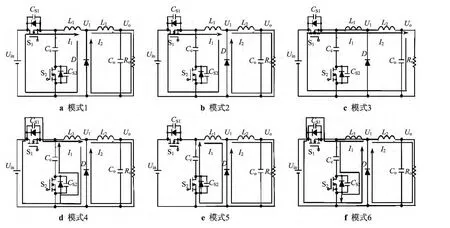
图3 6种电路等效模式

当下一个周期开始时，开关S1导通实现零电压开通.由模式分析再根据电容Cc的能量平衡可以得到以下方程:

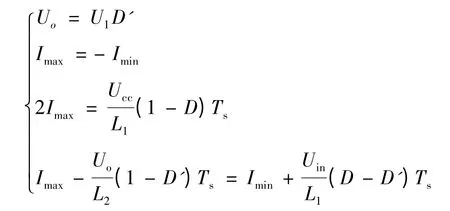
解得:

通过模式5可得:

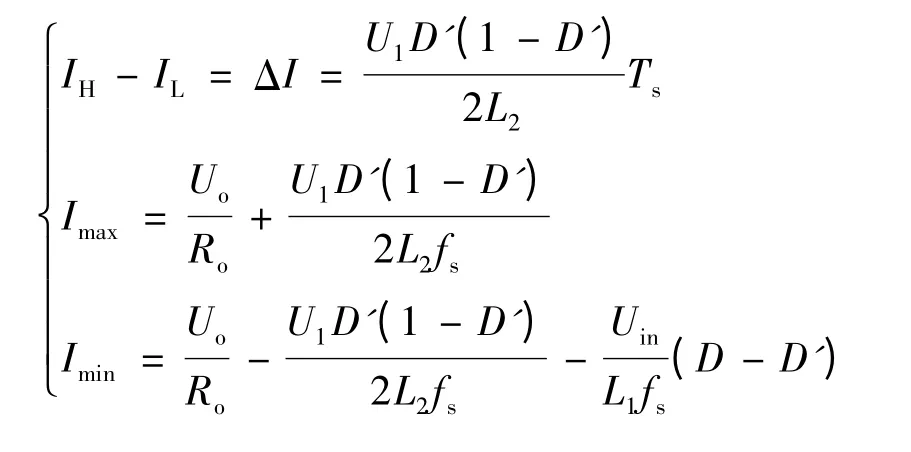
解得:

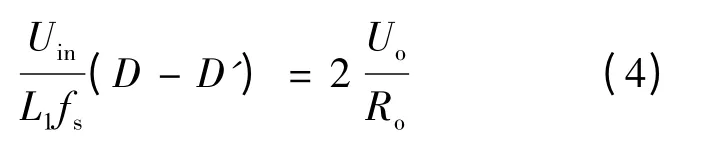
由式(2)和式(4)可得:

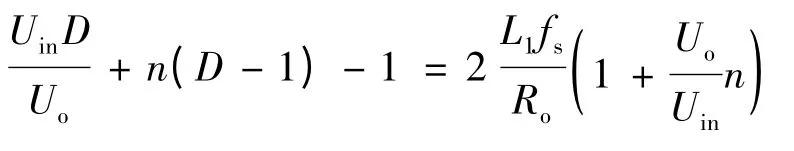
假设Uo=Uink，得到:

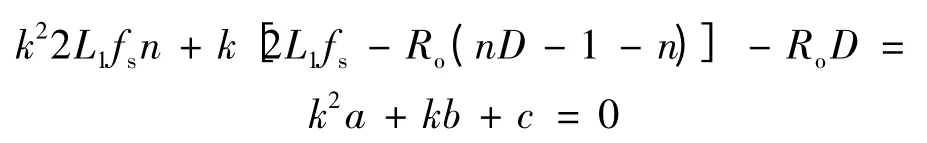
因此，该直流变换器的输出电压为:

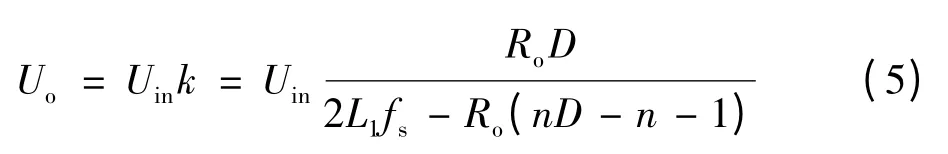
通过比较k和D的值，可得:

由式(6)可知，在占空比相同的情况下，相比传统单级DC-DC变换器，本文提出的DC-DC变换器具有更低的输出电压，能够实现较高的降压比.

1.3 软开关实现条件

本文提出的拓扑结构是通过电感电流对开关寄生电容充放电的方式实现软开关的导通.从上述原理分析可以看出，S1软开关导通的条件是由Imin对S2的寄生电容充电，对S1的寄生电容放电来实现的;而S2软开关导通的条件是由Imax对S1的寄生电容充电，对S2的寄生电容放电来实现的.电感电流I2的峰值可表示为:

所以电感电流的最大值和最小值可表示为:

S2的软开关极限条件为L1和Cs1与Cs2的谐振，能让Cs2上的电压谐振到零的条件可表示为:

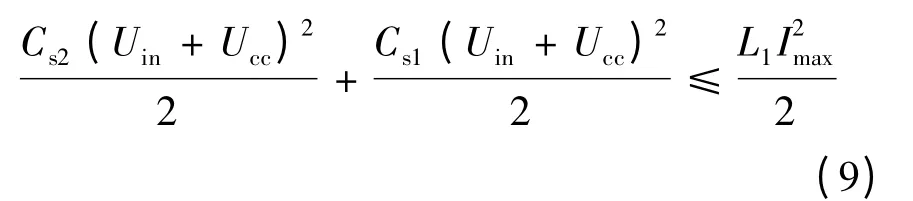
在实际应用中，Cs1和Cs2是两个非线性电容，会随电容上的电压发生变化.为了满足设计需要，可将其线性化，即开关的寄生电容Cs1和Cs2是两个固定容量的电容.

将式(8)代入式(9)可得:

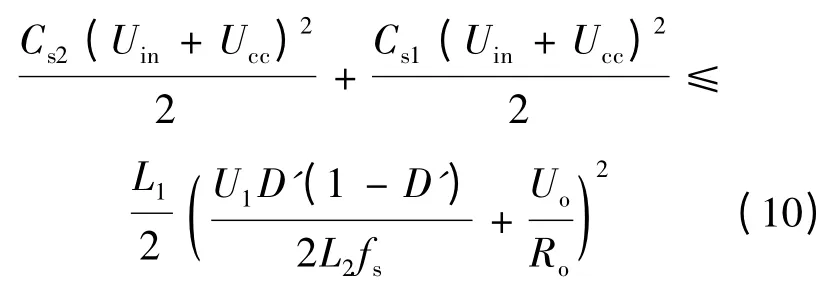
由于死区时间不可能非常大，所以可近似认为在死区时间内电感L1上的电流保持不变，即为一个恒流源对Cs2充电、Cs1放电.在这一情况下的软开关条件称为宽裕条件，其表达式为:

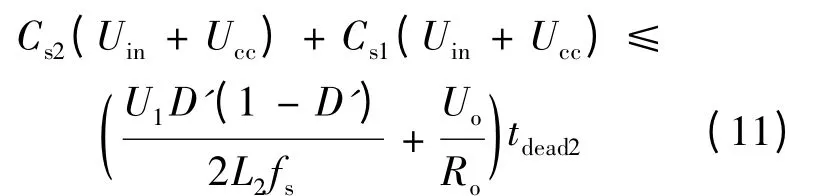
式中:tdead2——S2开通前的死区时间.

同理，S1的软开关宽裕条件为:

式中:tdead1——S1开通前的死区时间.

1.4 电容 Cc的选择

由模式分析可知，电容Cc的纹波范围与电感电流有关.由于Ucc是恒定值，故得到的电容Cc的纹波电压为:

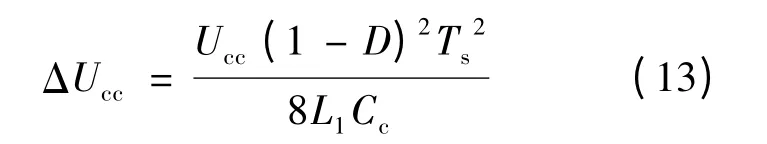
将式(3)代入式(13)可得:

从式(14)可以看出，当fs，Uo，Uin，D，L1不变时，根据Cc的纹波电压可以选取Cc的数值.

2 仿真验证

为了验证上述分析的正确性，采用表1的电路参数，利用PSIM仿真软件对本文提出的直流拓扑进行仿真.

表1 电路参数

该拓扑仿真的主要波形如图4所示.从图4可以看出，当开关S1导通，I1和I2线性上升、下降至I1=I2时，产生了实际占空比D'=0.09，约为D的 1/7，实现了高降压比，同时，U1为 134.67 V，约为Uin的1/3，通过式(1)和式(2)的计算可知，仿真结果正确.

要实现S1和S2的软开关，死区时间设定为0.05 μs.图 5 为开关的Ugs和Uds的波形.由图 5可知，在开关 S1导通时Uds1=0，实现了 S1的零电压开通，同理，S2也实现了零电压开通.图6为电压Ucc的波形.

图4 电路主要波形

图5 开关的Ugs和Uds的波形

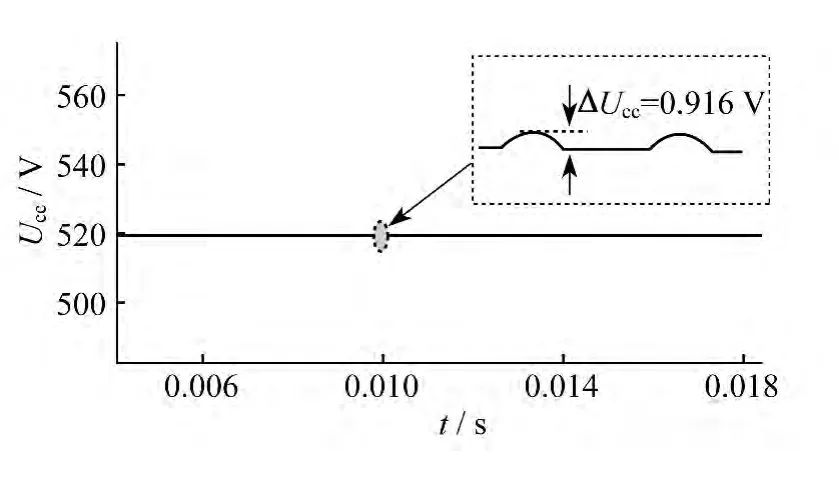
图6 电压Ucc的波形

从图6可以看出，当Ucc=520 V，Cc=10 μF时，ΔUcc=0.916 V，电容Cc的纹波为0.2%，小于1%，可以满足设计要求.

传统单级式、双级式和本文所提的直流变换器的占空比和输出电压关系如图7所示.由图7可以看出，本文中的直流变换器的输出电压呈线性增长，具有较好的PWM控制特性.在相同占空比下，传统单级直流变换器的降压比远低于其他两种DC-DC变换器，而本文的直流变换器的输出电压仅是双级 Buck变换器的1/11，因此该直流变换器具有高降压比特性.

图7 输出电压与占空比的关系比较

3 结语

本文提出了一种非隔离型高降压比软开关DC-DC变换器，该变换器采用单线结构，经过一级直流变换器直接与负载相连.仿真结果表明，该变换器具有较好的PWM控制特性;在满足一定死区时间内，开关S1和S2实现软开关导通，减小了开关的导通损耗.

[1]钱科军，袁越，石晓丹，等.分布式发电的环境效益分析[J].中国电机工程学报，2008，28(29):11-15.

[2]BLAABJERG F，TEODORESCU R，LISERRE M，et al.Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Trans. on Industrial Electronics，2006，53(5):1 398-1 409.

[3]ALLEE Guy.DC an idea whose time has come and gone[EB/OL].[2010-05-01].http:∥blogs.intel.com/research/2010/05/dc_-_an_idea_whose_time_has_co.php.

[4]王毅，张丽荣，李和明，等.风电直流微网的电压分层协调控制[J].中国电机工程学报，2013，33(4):16-24.

[5]吴卫民，何远彬，耿攀，等.直流微网中关键技术的研究[J].电工技术学报，2012，27(1):98-106.

[6]SALOMONSSON Daniel， SÖDER Lennart， SANNINO Ambar.An adaptive control system for a DC micro-grid for data centers[J]. IEEE Transactions on Industry Applications，2008，44(6):1 910-1 917.

[7]CUZNER R M，VENKATARAMANAN G.The status of DC micro-grid protection[C]∥ IEEE Industry Applications Society Annual Meeting，Edmonton，Alberta，Canada，2008:1-8.

[8]VISHWANATHAN N，RAMANARAYANAN V.A two stage power converter topology for high voltage dc power supplies under pulsed loads[J]. EPE Journal，2006，16(2):47-55.

[9]梁小国，危建，阮新波.一种新颖的交错并联正激三电平变换器[J].中国电机工程学报，2003，18(1):139-143.

[10]胡亮灯，孙驰，赵治华，等.宽范围高电压输入两级DC/DC辅助电源[J].高电压技术，2014(2):629-636.

[11]吕剑峰.两级DC/DC模块电源效率优化和环路特性的研究[D].哈尔滨:哈尔滨工业大学，2011.

[12]郑昕昕，肖岚.两级宽输入DC/DC变换器设计与建模分析[J].电力电子技术，2012，46(2):66-68.

[13]温振霖，阮新波，任小永.高压输入低压多路输出的两级式变换器[J].电工技术学报，2010，25(1):91-96.