一种新型序量分离与谐波检测技术

屈克庆，叶天凯，赵晋斌，李 芬

(上海电力学院 电气工程学院，上海 200090)

随着电力电子技术的发展，越来越多的新能源发电系统接入电网，使得并网同步化技术成为研究热点.[1-2]同时，基于电网稳定性的考虑，要求新能源发电系统具备一定的故障穿越能力，通常需要提取电压的序分量来实现控制策略，因而在电网故障条件下，如何快速、准确地从含有未知谐波的电网电压中提取电压各序分量具有重要的研究意义.[3-4]

目前，新能源并网发电系统常用锁相环(Phase-Locked Loop，PLL)技术进行电网频率和相位的同步.在理想对称电压情况下，同步坐标下的锁相环(Synchronous Reference Frame PLL，SRF-PLL)能够快速精确地实现频率和相位的跟踪，[5]然而在电网故障时，其应用效果无法满足要求.[6]为了克服 SRF-PLL鲁棒性较差的缺点，文献[7]提出了双同步坐标系下的锁相环技术(Double Synchronous Reference Frame PLL，DSRF-PLL).DSRF-PLL可以同时检测电网电压正、负序分量的频率和相位，大大提高了PLL在电网故障时的性能.因此，从含有未知谐波的电网电压中，检测电压正、负序分量的快速性与准确性决定了DSRF-PLL的性能优劣.

文献[8]给出了一种在同步坐标下，利用正负序电压旋转方向相反的性质，实现序量分离的方法.在正序坐标下，正序分量变为直流量，而负序分量变为2倍频交流量，用低通滤波器滤除交流量即可实现正序分量的分离;同样，在负序坐标下，也能实现负序分量的分离.但由于存在低通滤波器，使得这种方法易受低次谐波的干扰，影响系统动态性能，并且同步坐标的引入增加了计算量.文献[9]和文献[10]提出了使用二阶广义积分器(Second Order Generalized Integration，SOGI)实现序量分离.SOGI实质上是一种特定频率信号能通过的带通滤波器，而且输出两个相互正交的信号，利用这两个正交信号进行代数运算即可得到正负序分量.但由于SOGI是二阶积分器，不具备极性选择功能，因此需要附加运算来完成极性选择.为此，本文提出了一种静止坐标下的序量分离及谐波检测技术.该方法通过构建具备可选择指定频率与极性功能的一阶带通滤波器(First Order Band Pass Filter，FOBPF)，采用简便的结构即能实现序量分离和谐波检测，对于新能源并网系统具有一定的理论参考和应用价值.

1 FOBPF的基本原理

由控制学原理可知，理想带通滤波器有一定的带宽，频率在这个带宽范围内的信号经过滤波器后既不会衰减也不会放大，频率不在这个带宽范围内的信号均会被滤除.利用带通滤波器这一特性，设定一个带宽包含目标信号频率在内的带通滤波器即可得到目标信号.SOGI就是一个典型的带通滤波器，其传递函数为:

式中:k——与SOGI品质因数相关的可调参数;

ω0——SOGI的谐振频率.

由传递函数可以得到D(s)的幅频特性为:

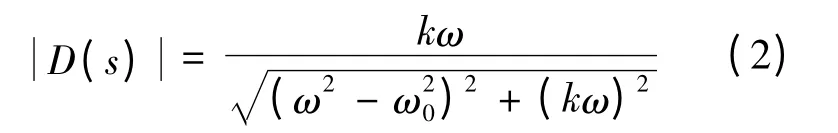
取谐振频率 ω0为50 Hz，系数k为 1.414.由其幅频特性可知，在频率为±50 Hz处，幅值的衰减为0 dB，其他频率处均存在不同程度的衰减.这表明SOGI具有较好的频率选择能力，但也说明SOGI无法选择频率的极性.

然而FOBPF能很好地弥补SOGI在频率极性选择上的不足，其传递函数为:

式中:ωb——FOBPF 的带宽;

kω0——中心频率.

可以得到G(s)的幅频特性为:

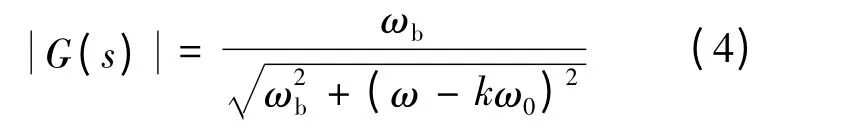
取中心频率kω0为 50 Hz，带宽 ωb为 20 rad/s.同样，由其幅频特性可知，FOBPF不仅具备与SOGI同样的频率选择能力，还具有频率极性选择功能.

对滤波器性能的评估通常包含两方面:一是滤波效果，即准确性;二是响应速度，即快速性.FOBPF的滤波性能由其传递函数G(s)决定，从G(s)的表达式可知，FOBPF的滤波性能与带宽ωb的选择直接相关.带宽越大时，中心频率附近信号的衰减率越小，表明滤波效果越差.然而，更大的带宽意味着更好的动态性能，因此在选择FOBPF的参数时只能在快速性与准确性中进行折衷.在反馈回路中需要不断更新反馈信号，快速性比准确性更为重要;而在处理需要进行计算的信号时，准确性又比快速性更为重要.因此，需要根据不同的应用场合选择合适的参数.

2 FOBPF的实现方法

根据上述原理分析，FOBPF设计的关键是传递函数G(s)的实现.在静止αβ坐标下，有:

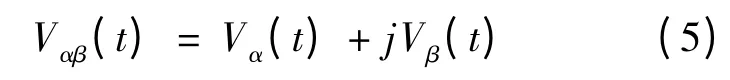
对V(t)进行拉普拉斯变换，得到:

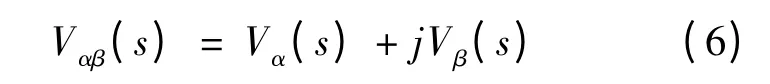
信号V(t)在时域中通过滤波器，在拉普拉斯频域内表现为乘以这个滤波器的传递函数，于是有:

由式(7)可以得到:

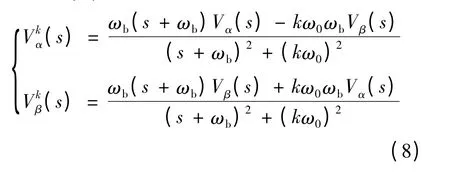
对式(8)进行简化可得:

由式(9)可以得到FOBPF的实现方法，其结构如图1所示.输入信号经过αβ变换输入到图示结构中，并设定中心频率kω0和带宽 ωb，即可实现一个中心频率和带宽确定的FOBPF.

图1 FOBPF的结构示意

3 FOBPF的应用及仿真分析

3.1 在序量分离中的应用

为了验证FOBPF在序量分离应用中的良好性能，对电网电压出现幅值不平衡情况进行了仿真.在Matlab仿真条件下，设定三相不平衡电网条件如下:电网电压频率为50 Hz，abc三相电压幅值分别为150 V，200 V，240 V.由于正负序分量频率分别为 ±50 Hz，所以需要两个FOBPF级联实现分离.具体方法如图2所示.

图2中，两个FOBPF分别完成一个特定频率分量的提取，FOBPF1的中心频率设定为 100π rad/s，用于提取正序分量;FOBPF2的中心频率设定为－100π rad/s，用于提取负序分量.两个滤波器有相同的带宽，设定为50 rad/s.

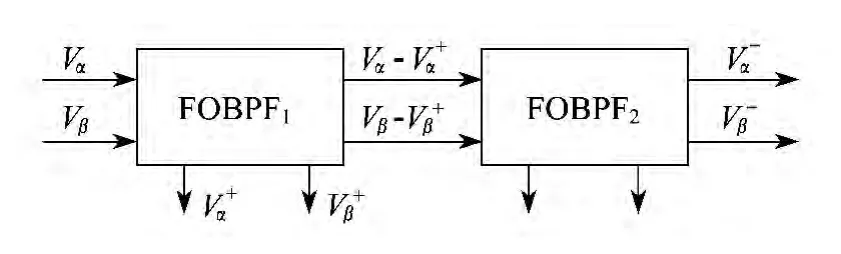
图2 FOBPF在序量分离中的应用示意

图3 为序量分离仿真结果.结果表明，FOBPF能够准确快速地实现正负序分量分离.在同样的准确性条件下，与传统SOGI实现序量分离的方法相比，完成分离时间由0.12 s减少到0.08 s，故本方案能有效缩短动态响应时间.

图3 序量分离仿真结果

3.2 在同步化中的应用

在电网不平衡条件下，电网电压的同步通常采用正负序坐标下分别锁定频率和相位的方法来实现.这样，FOBPF在电网同步中的应用是在序量分离的基础上进行的.首先，对输入信号进行正负序分量分离;然后，分别用 SRF-PLL进行正负分量的相位锁定，如图4所示.

图4 FOBPF在同步化中的应用示意

仿真实验是在序量分离的基础上进行的，正序分量频率检测结果如图5所示.FOBPF提取的正序分量是三相对称的，这使得SRF-PLL在电压对称情况下的优越性能得到很好的体现.由图5可以看出，稳态输出频率几乎不存在波动，这表明基于FOBPF的SRF-PLL是一种性能优越的电网同步化技术.

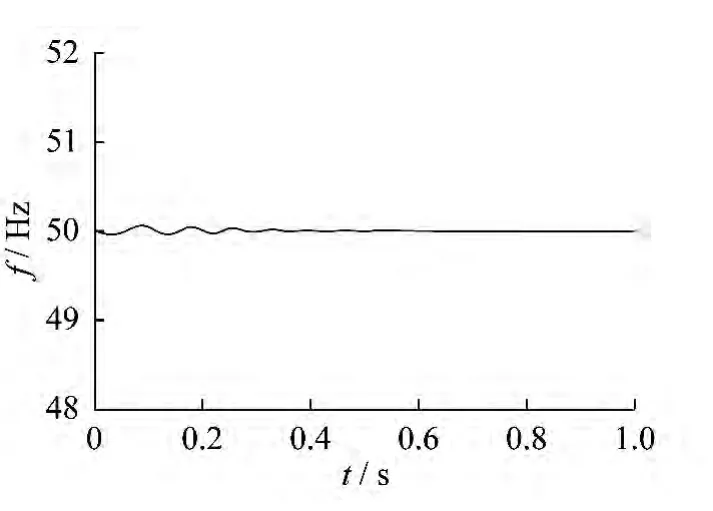
图5 正序分量频率检测结果

3.3 在谐波检测中的应用

FOBPF在谐波检测方面同样具有良好的性能，如图6所示.为了实现k种不同次数谐波的分量，需要k个中心频率与谐波频率相对应的FOBPF，每个FOBPF实现对一种谐波的检测.

图6 FOBPF在谐波检测中的应用示意

为了验证FOBPF的谐波检测性能，进行了如下仿真.设定输入信号除基波分量外，还包含3次、5次、7次谐波分量，且这些谐波分量的幅值均为基频分量幅值的10%，并加入幅值为2%基波幅值的15次、17次谐波以模拟噪声干扰信号.图7为5次谐波分量输出结果.

图7 5次谐波检测结果

此外，基波分量、3次谐波及7次谐波有相似的输出，由于篇幅的原因没有列出.仿真结果表明，FOBPF能够从严重污染的信号中检测分离任意频率的谐波分量.

4 结语

本文提出了一种静止坐标下的序量分离与谐波检测技术.该方法通过构建具备指定频率选择并带有极性选择功能的一阶带通滤波器，采用简便的结构即能实现序量分离、同步化和谐波检测等典型应用.仿真结果表明，所提出的方法表现出了良好的性能.

[1]FERREIRA R J，ARA U'JO R E，PECAS Lopes J A.A comparative analysis and implementation of various PLL techniques applied to single-phase grids[C]∥ Energetics(IYCE)，Proceedings of the 2011 3rd International Youth Conference on IEEE，2011:1-8.

[2]NICASTRI A，NAGLIERO A.Comparison and evaluation of the PLL techniques for the design of the grid-connected inverter systems[C]∥Industrial Electronics(ISIE)，2010 IEEE International Symposium on IEEE，2010:3 865-3 870.

[3]TIMBUS A， LISERRE M， Teodorescu R，et al.Synchronization methods for three phase distributed power generation systems-An overview and evaluation[C]∥Power Electronics Specialists Conference，2005:2 474-2 481.

[4]YAZDANI D，MOJIRI M，BAKHSHAI A，et al.A fast and accurate synchronization technique for extraction of symmetrical components[J]. Power Electronics，IEEE Transactions on，2009，24(3):674-684.

[5]王宝诚，伞国成，郭小强，等.分布式发电系统电网同步锁相技术[J].中国电机工程学报，2013，33(1):50-55.

[6]王鹿军，张冲，吕征宇.电网谐波背景下单相并网逆变器的锁相方法[J].电力系统自动化，2013，37(14):107-112.

[7]RODRIGUEZ P，POU J，BERGAS J，et al. Double synchronous reference frame PLL for power converters control[C]∥ Power Electronics Specialists Conference，2005:1 415-1 421.

[8]ALEPUZ S，BUSQUETS S，BORDONAU J，et al.Fast on-line symmetrical components separation method for synchronization and control purposes in three phase distributed power generation systems[C]∥Power Electronics and Applications，European Conference on.IEEE，2007:1-10.

[9]RODRIGUEZ P，TEODORESCU R，CANDELA I，et al.New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions[C]∥Power Electronics Specialists Conference，2006:1-7.

[10]陈艳艳，沈旦立，皇淼淼，等.基于二阶广义积分器的单相并网锁相环的研究[J].电力电子技术，2013(5):46-47.