浅谈高等数学教学中数学建模思想的渗透

吴志强

（甘肃畜牧工程职业技术学院 甘肃 733006）

浅谈高等数学教学中数学建模思想的渗透

吴志强

（甘肃畜牧工程职业技术学院 甘肃 733006）

随着科学技术进步和社会发展的日新月异，高职院校的数学教学也顺应时代发展需求进行了诸多方面的改革探索：淡化理论体系的推导与复杂的计算，强化数学概念的建立及数学的实践性、应用性；在数学教学中引入数学建模的内容，把数学和实际应用问题联系起来等。其中，数学建模思想的渗人极大地促进了高职院校数学教学的改革与创新，进而达到提高教学和科研能力的效果。

虽然高等数学课程本身的内容多，课时不够，但我们将数学建模的思想融入高等数学课程中，并不是用“数学建模”课的内容抢占高等数学课程的课时，在此，仅从两个方面将数学建模的思想逐步渗透到高等数学的教学中。

一、在高等数学的概念中融入数学建模的思想

从广义上讲，高等数学教材中的导数、定积分等复杂抽象的概念都来源于实际。因此在讲授这些概念时可以恰当选取一些生动的实例来吸引学生的注意力，同时将概念模型自然地建立起来，使学生充分感受到实际问题向数学的转化。为了在概念的引入中展现数学建模，首先必须提出具有实际背景的引例。下面我们就以高等数学中导数这一概念为例加以说明。

引例：变速直线运动的瞬时速度

1。提出问题：设有一物体在作变速直线运动，如何求它在任一时刻的瞬时速度？

2。建立模型：物体沿直线的运动可理想化为质点在数轴上的运动。假设质点在t=0时刻位于数轴的原点，在任意的时刻t，质点在数轴上的坐标为s=s(t)。下面讨论质点在时刻的瞬时速度即：已知质点的运动方程s=s(t)，求瞬时速度

质点从t0到这段时间间隔内通过的路程为

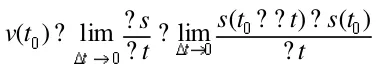
上式即为己知物体运动的位移函数s=s（t），求物体运动到任一时刻t0时的瞬时速度的数学模型。这个模型,我们抛开它的实际意义单从数学结构上看，可归结为一个数学模型，即求函数改变量与自变量改变量比值，当自变量改变量趋近于零时的极限值。由此,我们引入函数的导数定义

定义设函数y=f（x）在点x0的某个邻域内有定义，当自变量x在点x0处取得改变量△x(x0+△x仍在该邻域内△x≠0，且)时，相应的函数改变量

存在，则称函数y=f(x)在点x0可导，并称此极限值为函数y=f(x)在点x0处的导数，记作

二、在高职高等数学教学中,将数学建模案例与定理讲解相结合

例如,在介绍条件极值的时候,可以与“奶制品的生产与销售”这个建模例子结合起来讲解,通过教师的引导,将条件极值和这个问题联系起来,找到它们之间的关系,用数学建模的思想解决这个实际问题。在讲解极值定理时,可以增加简单的优化模型,例如与“存贮模型”“生猪出售时机”“最优价格”等数学模型相结合。通过这些实际问题的模型,学生能更好理解高等数学中定理,并学会应用定理解决实际问题。

三、在高等数学习题课教学中可以增加建模案例教学的环节

数学建模案例的难易程度应与高职学生的知识水平和学习能力相符,过于简单或过于困难都不利培养学生的学习兴趣,要选取难易适当、与现实生活相关的实际问题,例如,在微分中值定理及导数应用这一章习题课中可以增加“消费者选择”数学模型;在积分知识及其应用这一章习题课中可以增加“存储问题”数学模型等等。通过对这些与现实相关的问题的研究,学生能清楚地认识到高等数学在实际问题中的应用,从而积极主动地应用数学知识分析问题、解决问题。

四、在高等数学课程的考核中增加数学建模问题

学完每章节的内容后,在课外作业的布置中,除书本中的习题外可以再增加一两道需要运用本章知识解决的实际问题的数学建模题目,这些数学建模可以让学生独立或自由组合成小组去完成,给予完成情况好的学生较高的平时分,在期末考试试题中以附加题的形式增加数学建模的题目。用这种方法,鼓励学生应用数学的知识解决现实中各种问题,提高学生使用数学知识解题的能力,调动学生的学习积极性,从而使学生获得除数学知识本身以外的素质与创新能力。

在高等数学教学中融入数学建模思想,培养学生的建模能力,是符合当代人才培养要求的,是可行的。数学建模思想的融入要采用渐进的方式,尽量与已有的教学内容进行有机的结合。实践证明,通过在高等数学教学中融入数学建模思想,不仅激发了学生的学习兴趣,培养了学生的创新能力,还可以促进教师进行自我提升。但如何在高等数学教学中很好地融入数学建模思想目前还处于探索阶段,仍需要广大数学教师的共同努力。