基于小波阈值组合滤波器的光谱去噪方法

黄敏超， 高美凤

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡214122)

光谱仪器是分析物质物理化学组成的重要分析仪器。近些年来，光谱仪已经广泛应用到生产和生活中。在一些现代大型钢铁企业，分析检测系统已成为生产过程中质量控制与管理，以及企业经营销售活动不可或缺的重要组成部分，而光电直读光谱仪是钢铁行业的主要分析检测校准仪器。钢铁行业中可以利用光电直读光谱仪读取所炼钢铁的不同成分，因此可以通过控制不同成分制作出不同的钢铁样品。根据光谱检测器件的不同，目前市场上的光电直读光谱仪主要有两种:基于光电倍增管(PMT)和基于电荷耦合器件(Charge-coupled Device，CCD)的光谱仪。虽然基于PMT 的光电直读光谱仪测量精度很高，但其存在谱线通道受限，机械结构复杂，体积庞大等缺点，这些缺陷使得光电倍增管光谱仪无法达到在野外操作或者多波长的检测要求，因此依然无法广泛推广和应用。而基于CCD 的光电直读光谱仪具有体积小，质量轻，功耗低，使用方便，操作简单，易校准，单次采集光谱范围宽，响应速度快，灵敏度高，数据采集处理快捷方便等特点。所以这种光谱仪已经成为研究的重点，并迅速从实验室研究转向实际应用阶段［1-2］。

线阵CCD 的数据采集是一个重要的步骤，由线阵CCD 采集到的光谱数据会含有多种噪声，包括由杂散光引起的低频背景噪声和由暗电流噪声、转移噪声所组成的高频噪声。这些噪声在光谱图上会形成波动和毛刺，对光谱的峰值位置和波峰的高度会产生一定的影响，因此需要对光谱的数据进行去噪处理。常用的去噪算法有很多种，如均值滤波，平滑滤波，窗函数法，自适应中值滤波，中值滤波和小波变换滤波［3］。根据CCD 采集到的光谱特性以及各种去噪方法的特点，文中采用小波阈值和中值滤波相结合的方法对含噪光谱数据进行处理。

1 信号去噪算法描述

1.1 小波阈值法去噪原理

1994 年Donoho 和Johnstone 提出了小波阈值收缩法(Wavelet Shrinkage)，该方法用于信号去噪的主要思想是:对信号进行小波分解，再提取出高频系数，将小波系数大于阈值部分的视为有用信号，小于阈值部分的那部分归为噪声，最后对得到的低频系数和高频系数进行重组［4］。

设含噪信号为

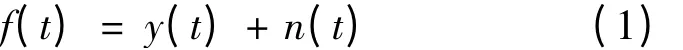
其中，y(t)为有用信号;n(t)为噪声。小波阈值去噪的步骤如下:

1)小波分解。选择合适的小波和分解层数对含噪信号f(x)进行小波分解，获得小波分解系数。

2)阈值处理。选择合适的阈值T，对小波分解的高频系数进行阈值处理。

3)小波重组。利用1)和2)得到的小波低频系数和各层高频系数进行小波反变换，最终得到信号估计值^f，即去噪后的信号［5］。

在小波阈值去噪算法中，对小波高频系数阈值处理所选取的阈值函数不同反映了对小波稀疏模的处理策略不同，通常阈值函数有硬阈值函数(Hard Threshold Function)和软阈值函数(Soft Threshold Function)两种。硬阈值可以保护好局部特性，软阈值处理数据相对平滑，但是边缘会相对模糊［6-7］。硬阈值和软阈值函数的表达式分别为［8］硬阈值函数

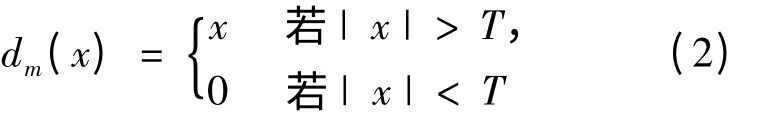
软阈值函数

对于小波阈值的关键是取合适的阈值T，阈值取的太大则可能会过滤到需要的有用信号，如果阈值取的太小就可能会参杂较多的噪声，达不到预期的效果。文中直接调用Matlab 中的阈值函数进行阈值选择，这样可使计算更加方便，速度也更快。在Matlab 中，获取小波阈值包括ddencmp，thselect，wbmpen 和wwdcbm 4 种函数。这4 种函数各有特点，由于ddencmp 函数获取阈值灵活，所以文中选择ddencmp 函数获取全局阈值T，获取阈值T 的函数为

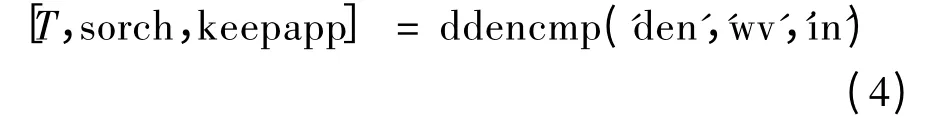
其中，in 为输入的信号。

1.2 中值滤波描述

中值滤波是Turkey 首先提出并应用于一维信号的去噪。中值滤波是利用抽样数据滑动窗口在光谱数据上滑动的非线性去噪方法，对窗口中的抽样值进行重新排序，将正中的数值与窗口中抽样数据的中间值进行替换［9-10］。

假设滑动窗口的长度为n = 2k +1 或n = 2k，N是光谱数据的个数，且必须N ≥n。当窗口在光谱数据上滑动时，中值滤波器输出的中值为

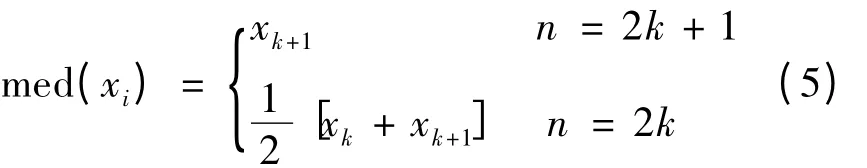
为了保证取得中值的便利性，一般所取窗口的长度都是奇数。根据中值滤波降噪原理，中值滤波去噪的步骤如下［11-12］:

1)窗口宽度的确定和数据排序。选择合适的窗口宽度，再将窗口内所有光谱数据由从小到大进行排序。

2)求出中值。排序后窗口内中间位置的值或者两个中间位置的平均值即为该窗口的中值。

3)中值替换。利用1)和2)所求的中值代替原来光谱数据中间位置的数值。

中值滤波器的优点在于:通过中值滤波器得到的数据总是可以在滑动窗口中输入的原始光谱数据中找到，不增加新的数据，保证了数据分析的准确性［3］。

1.3 改进的光谱去噪方法

由线阵CCD 的特性可以得知:光电直读光谱仪所获得的光谱数据含有高斯白噪声和较强的脉冲噪声，而小波阈值去噪法不能很好地去除脉冲噪声。因此，文中给出了一种组合去噪方法—— 小波阈值法和中值滤波相结合的光谱去噪方法。组合去噪方法存在两种模式。

1)模式1。首先对含噪信号f(x)进行小波阈值处理，得到处理后的信号;再对f^(x)进行中值滤波，其相应的数学表达式为

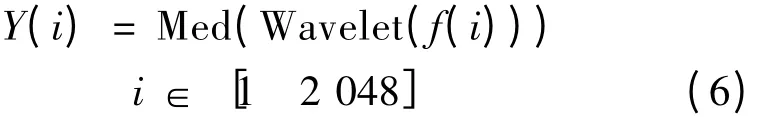
2)模式2。首先对含噪信号f(x)进行中值滤波，然后再进行小波阈值处理，其数学表达式为

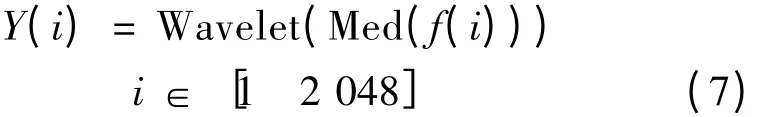
2 仿真结果与讨论

在完全处于暖室的条件下搭建好硬件电路后进行实验。将光源通过狭缝光栅和透镜照射到线阵CCD 上，得到如图1 所示的含噪声的CCD 信号。

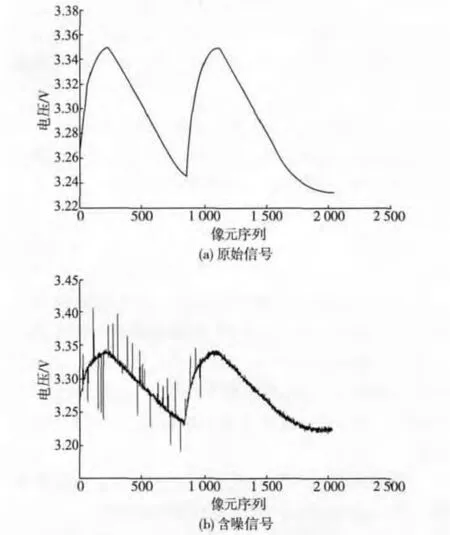
图1 含噪声的CCD 信号Fig.1 CCD signal with noise

首先选用小波基db4 对图1(b)的含噪信号进行小波阈值处理，分别对其进行3 层阈值分解，5 层阈值分解和7 层阈值分解，计算出经过不同阶层处理的光谱曲线的信噪比(SNR)，比较小波变换不同层次的去噪效果。表1 为小波阈值去噪方法的信噪比对比，图2 为5 层小波阈值滤波效果。

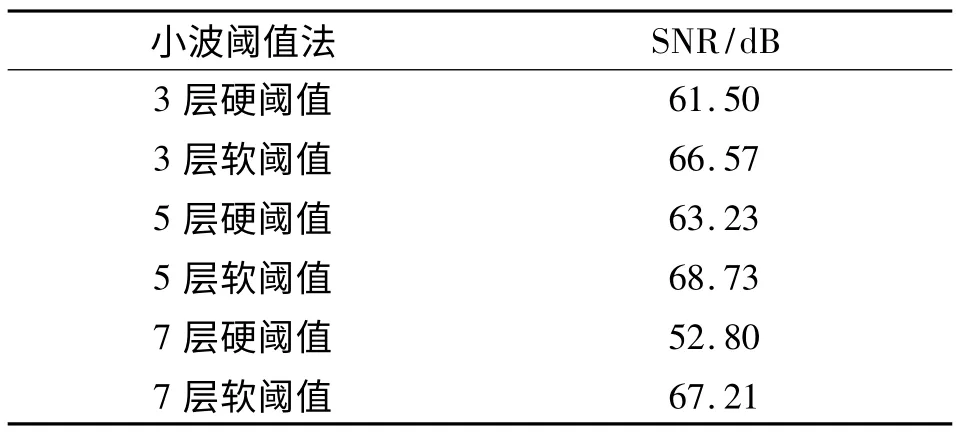
表1 小波阈值去噪信噪比对比Tab.1 SNR comparison of the wavelet threshold

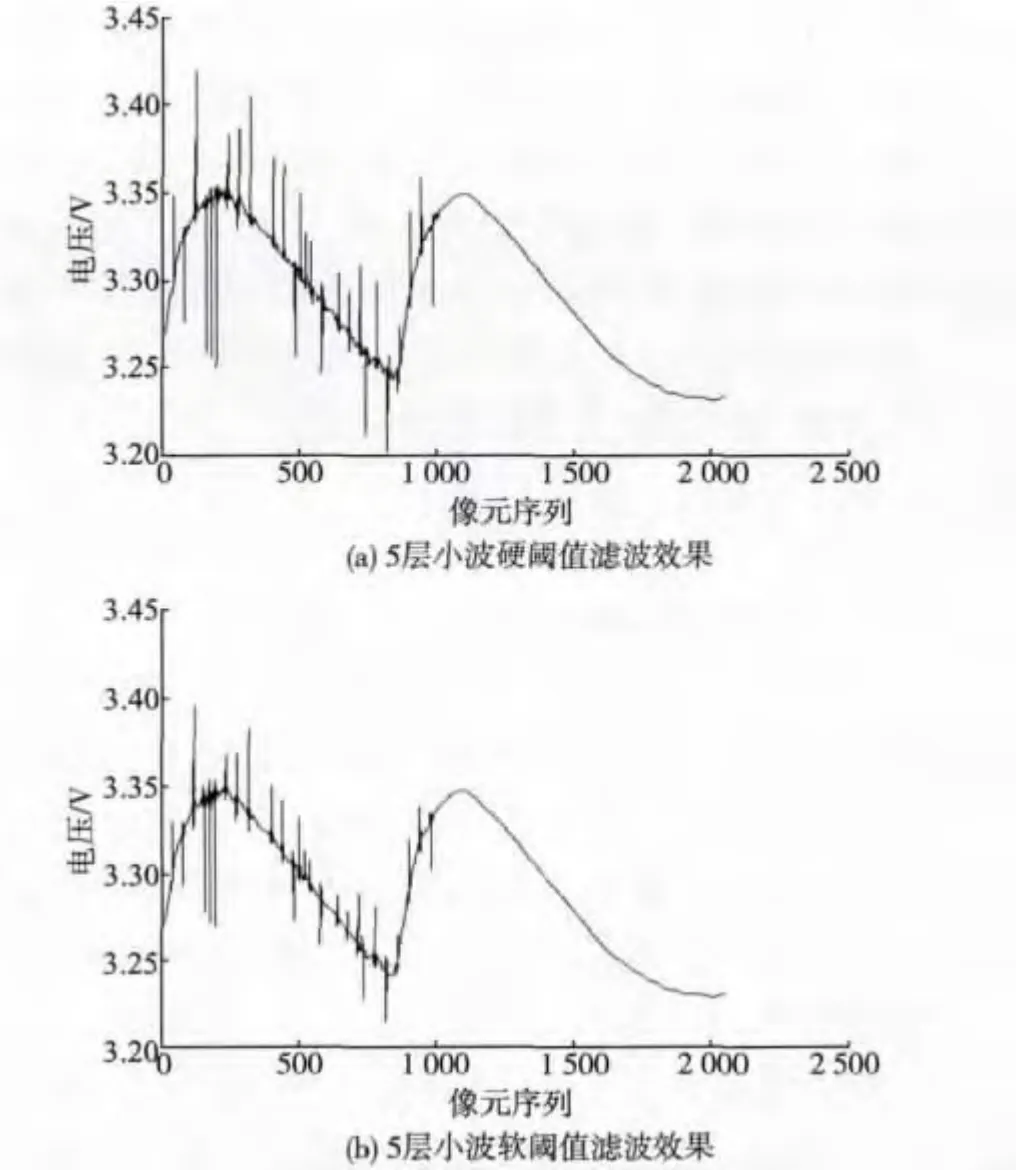
图2 5 层小波阈值滤波效果Fig.2 Effect diagram of 5 layers wavelet threshold

由表1，图2 可以得到:小波阈值在处理高斯白噪声有比较好的效果，但是对于脉冲噪声效果不是很好，依然保留了许多的毛刺。另外，对比不同层次的硬阈值和软阈值的效果可以看出，软阈值的处理要比硬阈值处理更加合适，而且在5 层小波软阈值时滤波效果最为明显。

针对于脉冲噪声，采用中值滤波对CCD 信号进行处理。中值滤波的关键在于窗口宽度的选择，故文中选择窗口宽度从n = 7 开始滤波，每次实验窗口宽度增加4 个，对比每次滤波的效果图和信噪比，以此作为依据判断中值滤波的滤波效果。表2 为各个窗口长度滤波后所求的信噪比。

表2 中值滤波不同窗口长度的信噪比对比Tab.2 SNR comparison of different window lengths median filter

由表2 可知:当窗口宽度从n = 7 依次增大时，信噪比随之增高;当n ＞31 时信噪比开始降低，n =31 时信号的信噪比最高;同时，表2 中的数据也表明了窗口宽度的大小直接影响到滤波效果的好坏。窗口过窄，会保留光谱数据里的部分噪声，同时还会影响数据的精确度;窗口太宽，则会把一些有用的信号去除。图3 为当n = 31 时的滤波效果。

文中选用信噪比(SNR)和均方根误差(RMSE)判断去噪效果的好坏。均方根误差也是标准误差，能够很好地反映测量值的精密度，这也是一般测量中广泛采用的原因。表3 列出了用不同方法对含噪信号进行去噪处理后的信噪比(SNR)和均方根误差(RMSE)。图3 为当n = 31 时的中值滤波效果。由表3 中的均方根误差RMSE 和信噪比SNR 可以看出，图3 中经过n = 31 的中值滤波处理后信号的均方根误差非常小，已经接近于原始信号，并且信噪比也得到很大提高。对于含有脉冲噪声的光谱数据而言，中值滤波是一种比较好的处理方法。但是为了更好地去除光谱信号中的高斯白噪声和脉冲噪声，采用文中所提出的基于小波阈值法的组合滤波器对含噪光谱进行去噪处理。选用窗口长度为31 的中值滤波和5 层小波软阈值这两种最优滤波器进行组合。

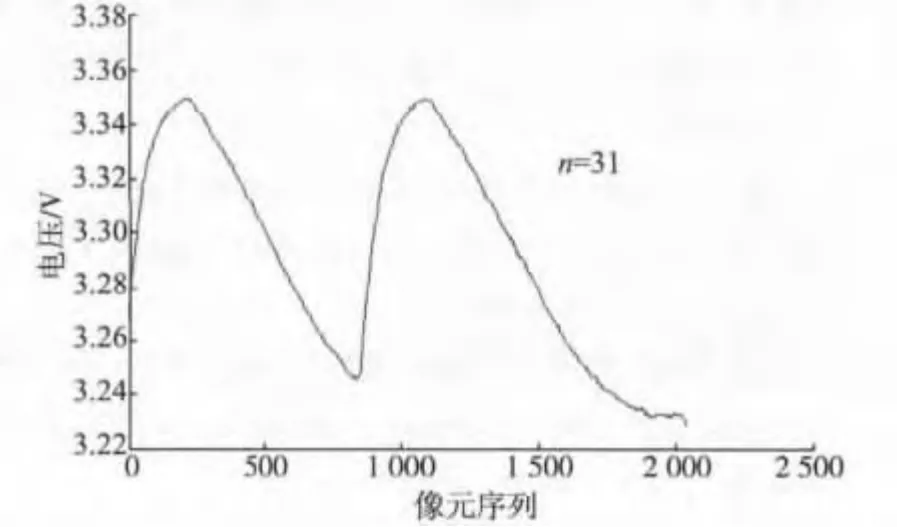
图3 n = 31 时的中值滤波效果Fig.3 Effect diagram of n = 31 median filter

表3 含噪信号和不同方法滤波之后的SNR 和RMSETab.3 SNR and RMSE of original signal and after different filtering theory

由表3 和文献［10］可以看出，小波阈值法对于高斯白噪声去噪效果比较好，而中值滤波对于脉冲噪声效果更优。根据文献［8］提出先小波阈值再中值滤波的组合滤波器的思想，文中在进行组合滤波器的实验中，对两种滤波的先后顺序进行研究和讨论。得到的结论是:经过模式1 组合滤波器处理后信号的信噪比是69.69 dB，均方误差为0.001 1;而经过模式2 组合滤波器滤波处理之后信号的信噪比是73.57，比模式1 提高了7.08%，均方误差为6.91 ×10－4，比模式1 降低了0.64%。并且经过模式2 去噪后的光谱信号的信噪比相比于表3 中含噪信号的信噪比提高了39.94%。因此，采用先中值滤波后进行小波阈值的模式2 使小波阈值和中值滤波的优点有机结合，对含噪信号可进行更有效的滤波。

3 结 语

针对光电直读光谱仪的光谱数据所含噪声的特点，提出了一种基于小波阈值的组合滤波算法，这种算法结合了小波阈值法和中值滤波的优点，对光电直读光谱仪的含噪光谱数据进行有效去噪，去噪后的光谱信号信噪比有明显提高，同时均方根误差也明显降低，能够非常接近于原始信号。综上所述，文中提出的组合滤波算法在处理含噪光谱数据是一种有效降噪算法。

［1］Rob Morris.Spectrometers move out of the lab［J］.Laser Focus World，2001，37(2):77-82.

［2］张叶根，叶反修.光电直读光谱仪技术［M］.北京:冶金工业出版社，2011:32-35.

［3］刘国宏，郭文明.改进的中值滤波去噪算法应用分析［J］.计算机工程与应用，2010，46(10):187-189.

LIU Guohong，GUO Wenming. Application of improved arithmetic of median filtering denoising［J］. Computer Engineering and Applications，2010，46(10):187-189.(in Chinese)

［4］Donoho D L，Iain M Johnstone.Ideal spatial adaptation by wavelet shrinkage［J］.Biometrika Trust，1994，9(3):425-455.

［5］田岩涛，常丹华.线阵CCD 信号的小波去噪方法研究［J］.传感技术学报，2005，18(2):250-253.

TIAN Yantao，CHANG Danhua.Study on wavelet removing noise for linear array CCD signal［J］.Chinese Journal of Sensors and Actuators，2005，18(2):250-253.(in Chinese)

［6］Donoho D L.Denoising by soft thresholding［J］.IEEE Transactions on Information Theory，1995，3(41):613-627.

［7］Golroudbari M A. Signal denoising based on wavelet transform using a multi-level threshold function［C］//Application of Information and Communication Technologies(AICT).Baku:IEEE，2013:1-5.

［8］刘艳萍，高果荣.提升小波变换与中值滤波结合的红外光谱消噪［J］.光谱学与光谱分析，2012，32(8):2085-2088.

LIU Yanping，GAO Guorong. Infrared spectrum denoising with combination of lifting，wavelet domain thresholding and median filtering［J］.Spectroscopy and Spectral Analysis，2012，32(8):2085-2088.(in Chinese)

［9］高浩军，杜宇人.中值滤波在图像处理中的应用［J］.电子工程师，2003，30(8):35-37.

GAO Haojun，DU Yuren.The application of median filtering on image processing［J］.Electronic Engineer，2003，30(8):35-37.(in Chinese)

［10］钱伟新，刘瑞根.一种改进的自适应中值滤波算法［J］.光学与光电技术，2011，9(4):35-38.

QIAN Weixin，LIU Ruigen.An improved adaptive median filtering algorithm［J］.Optics and Optoelectronic Technology，2011，9(4):35-38.(in Chinese)

［11］刘志宏，邓波.红外光谱预处理中去噪的研究［J］.光谱实验室，2006，23(4):815-819.

LIU Zhihong，DENG Bo.Study on denoising in pretreatment of infrared spectrum［J］.Chinese Journal of Spectroscopy Laboratory，2006，23(4):815-819.(in Chinese)

［12］WANG Yan，WANG Haibin，LIU Lihan.An improved wavelet threshold shrinkage algorithm for noise reduction of heart sounds［C］//Proceedings of the 2010 International Conference on Electrical and Control Engineering.Washington DC:IEEE Computer Society Washington，2010:5018-5021.