基于威布尔分布的汽车寿命估计方法
王亚菲,邬海峰
(1.天津大学管理与经济学部,天津300072;2.天津大学电子信息工程学院,天津300072)
现代汽车正不断向更智能、更高速、更复杂、更安全等方向发展,一旦汽车中某部件发生故障,将直接影响整个机车设备的正常运行,甚至威胁到消费者的人身财产安全。准确地预测汽车故障发生率,有助于提高汽车制造业的制造能力,提高汽车安全性能,降低汽车制造者的质保成本。汽车的可靠性分析是预测汽车故障的核心问题,对于汽车制造者和使用者至关重要。
汽车寿命概率分布的参数估计是可靠性分析的重要环节,只有通过参数估计建立合理、精确的统计学模型,才可以准确地预测汽车故障。通过分析汽车寿命数据对汽车寿命概率分布进行参数估计,是掌握汽车产品可靠性的关键。
威布尔分布作为一种可靠性模型,由于其合理化建模、数据拟合性好、解析表达式处理方便等优势,已经在很多领域得到了不同程度的应用与发展[1-9],它能有效地拟合产品全寿命阶段的寿命数据,也可用于模拟失效率的上升、恒定和下降情况。针对威布尔分布的汽车质保数据的参数估计问题,文中对比了极大似然参数估计法和神经网络估计法的精度,并通过实例验证了该方法的实用性,为商用汽车的可靠性评估提供直接而有效的参数估计方法。
1 威布尔分布模型
威布尔概率密度函数为
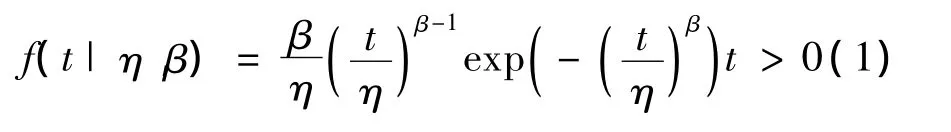
其中,t为汽车使用寿命;β为不同时期故障率曲线形状的参数;η为衡量平均故障间隔时间的尺度参数。威布尔累积分布函数为

生存函数S(t)和风险函数h(t)分别为
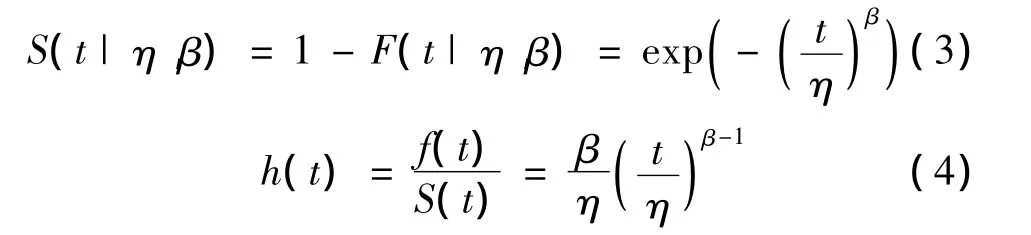
威布尔分布的密度函数、累积分布函数和风险函数分别如图1~图3所示。
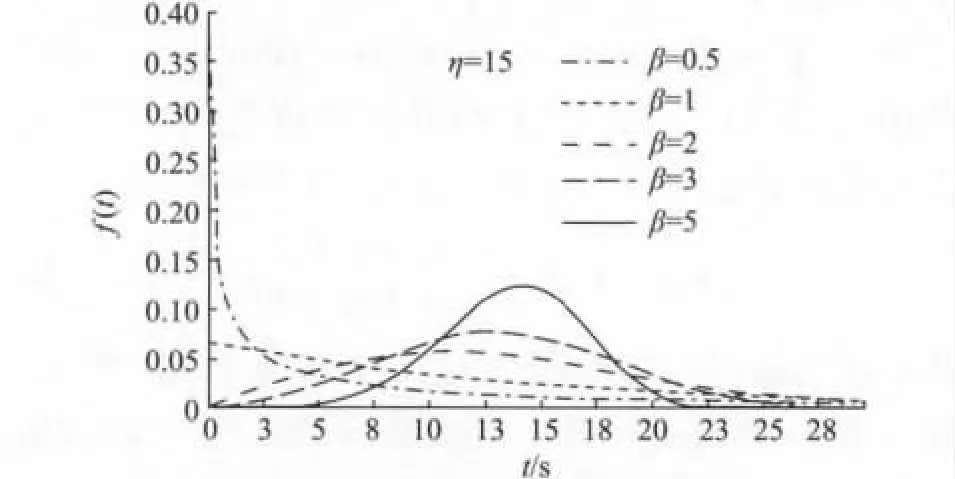
图1 威布尔分布的密度函数Fig.1 Probability density function of theWeibull distribution

图2 威布尔分布的累积分布函数Fig.2 Cumulative distribution function of the Weibull distribution
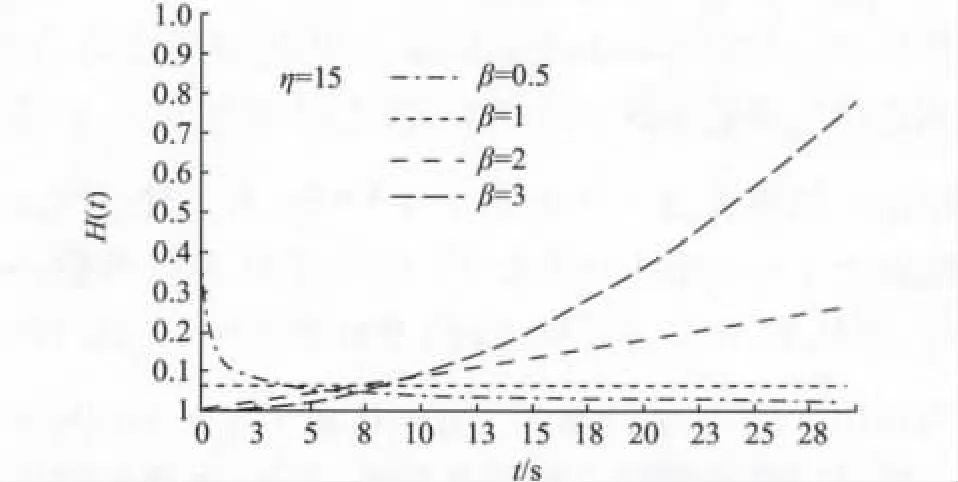
图3 威布尔分布的风险函数Fig.3 Hazard function of the Weibull distribution
由图1~图3中可以看出,形状参数β值的不同获得的曲线形状有很大区别。
2 浴盆曲线
汽车在使用寿命期内,故障发生率与使用时间有关。故障概率函数随时间t发生变化,汽车在不同时间段内故障率也不同。图4反映了设备全期的故障分布,包括早期故障、偶然故障和磨损故障,因其整体形状像浴盆,称为浴盆曲线[10]。
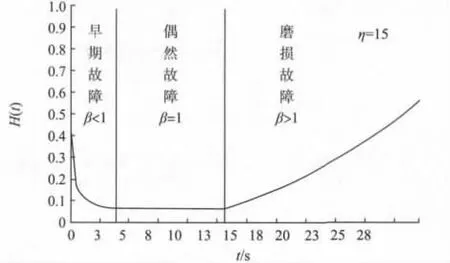
图4 浴盆曲线Fig.4 Bathtub curve
由图4可以看出,当β<1时,故障率函数h(t)呈递减分布,汽车有可能发生早期故障,适于建模早期失效;当β=1时,h(t)为常数,汽车有可能发生偶发故障,适于建模随机失效;当β>1时,h(t)呈递增分布,汽车有可能发生磨损故障,适于建模磨耗或老化失效。威布尔分布的3种故障率β<1,β=1,β>1,正好与浴盆曲线的3个阶段相对应。
3 参数估计
威布尔分布的参数估计可采用最小二乘估计法[1]、矩估计法[2]、平均秩次法[3]、相关系数估计法[4]、双线性回归法[5]、灰色估计法[6]、极大似然估计法[7]和人工神经网络法(ANN)[10]等。极大似然估计法在已知总体分布且样本容量足够大时,根据样本观测值出现的概率最大原则,估计总体中未知参数的估计值。极大似然估计法的结果大多具有无偏性、有效性和相合性,是一种最常见最有效的方法。神经网络法将神经网络模型引入汽车可靠性研究领域将有助于改进传统可靠性理论的操作方法,使可靠性模型的建模操作向着智能化方向发展,从而拓宽可靠性工程的应用领域。文中对比研究了极大似然估计法与神经网络法对汽车寿命数据进行参数估计的结果。
3.1 极大似然估计法
在可靠性分析中,极大似然估计法被广泛用于威布尔分布的参数估计。假设汽车寿命数据序列为ti,令xi为第i个样本发生故障的时间,其中i=1,2,…,N,N为本批次生产N台汽车进行寿命实验。威布尔分布的似然方程为
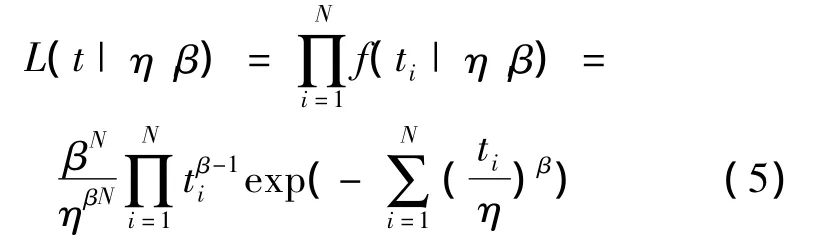
通过对似然方程求解偏导数,可得到模型参数的极大似然估计结果:

将式(6)、式(7)进一步整理得

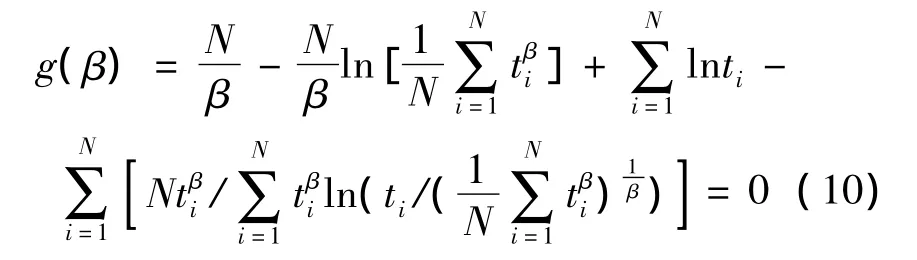
式(10)只有一个自变量β,属于单变量非线性方程,可通过Newton-Raphson迭代求解,形式如下:
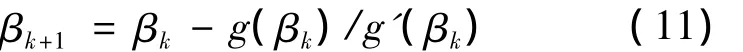
其中,βk为迭代过程中第k次得到的结果;β0为初始迭代值。初始迭代值对此算法的收敛性具有一定影响,一般机械系统寿命估计可取形状参数为1~10[9]。经过迭代后可以得到 β 的估计值。然后通过式(8)得到η的估计值。
3.2 人工神经网络法
在可靠性分析中,人工神经网络法作为一种数学模型被广泛地用于可靠性模型识别方法及参数估计方法中。神经网络通过W-H学习规则,或最小均方差算法(LMS)计算权值的变化,并且使网络误差的平方和最小化,能够训练神经网络模型的误差趋于最小值,且不需要导数,具有计算速度快和精度高的优点。
针对基于威布尔分布的可靠性模型,可以采用如图5中所示的神经网络结构进行参数估计。
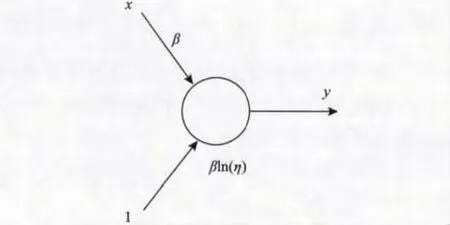
图5 威布尔分布参数估计的ANN结构Fig.5 ANN structure of the Weibull distribution
该ANN结构关系对应为一元线性方程:

使用式(12)和式(13)的变换,可以将威布尔分布函数变换为

利用文献[11]中的改进型近似中位秩式(15),可以直接计算经验分布函数Fn(ti)并计算得到y。
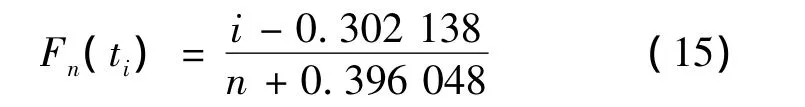
其中:i为故障汽车的顺序号;n为样本数量。将x,y输入ANN系统进行若干次训练,训练结束后得权值W即为形状参数β,阀值b为 -βln(η),从而得到β和η的估计值:

4 应用实例及分析
由实际工程经验可知,汽车寿命近似服从威布尔分布。选用某型号汽车进行寿命统计实验,在同样的生产条件下,样本数量为30,假设样本数据服从β=1.001,η=3 569的威布尔分布,具体数据见表1。
极大似然估计法基于Matlab仿真平台进行参数估计,采用Newton-Raphson法迭代若干次后,达到迭代结果收敛区间为2%,迭代时间为23.5 s。参数估计结果为=0.981=3 639。人工神经网络法基于Neuro Modeler Plus[12]仿真平台进行参数估计,采用W-H学习规则进行1 000次训练,训练时间为0.01 s。参数估计结果为=0.975=3 650。人工神经网络法的拟合结果如图6所示,收敛曲线如图7所示。
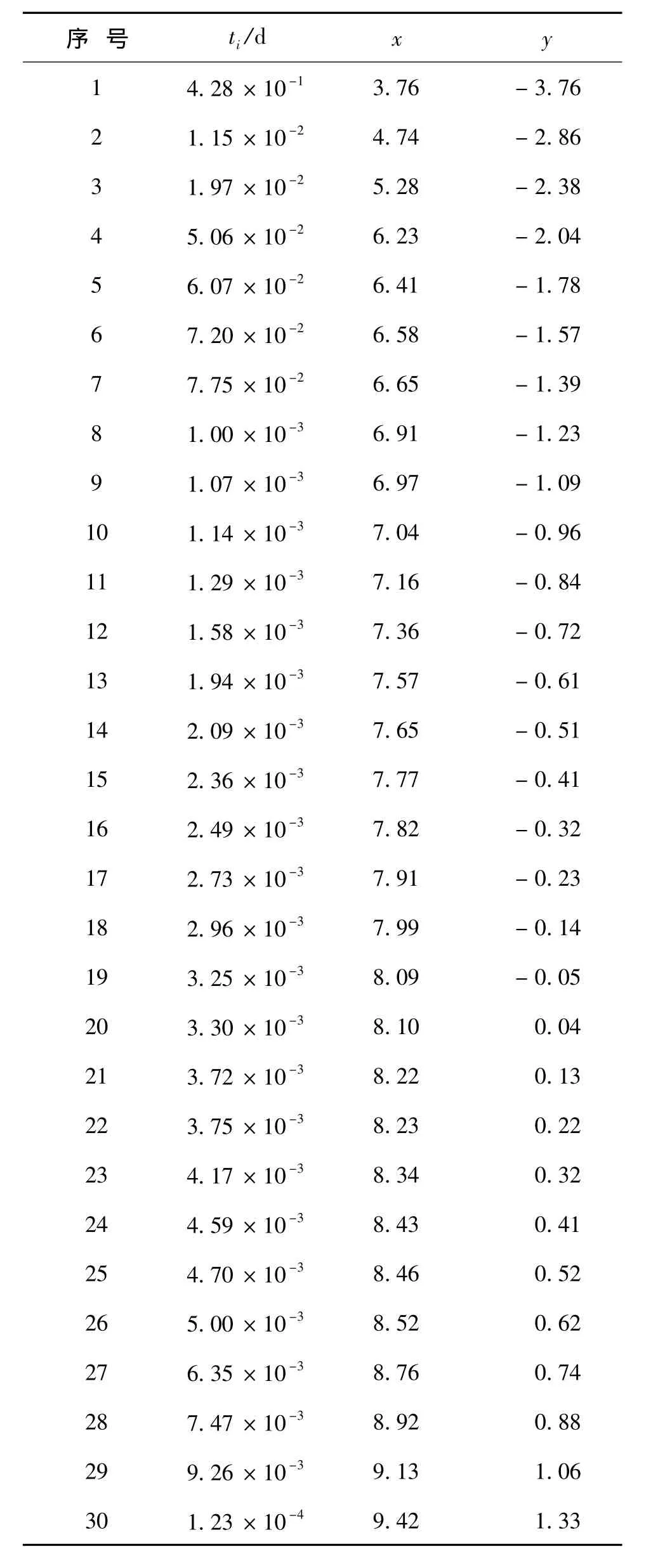
表1 汽车故障数据及中秩位法计算经验分布函数Tab.1 Automobile life data and calculation of the distribution function using rank-bitmethod

图6 人工神经网络法的拟合曲线Fig.6 ANN fitting results
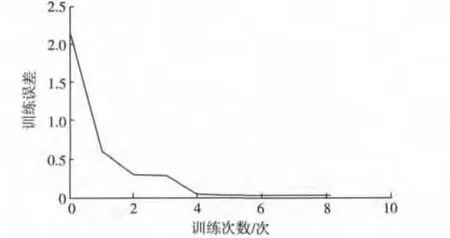
图7 人工神经网络的训练收敛曲线Fig.7 Convergence curve of ANN's training error
由图7可以看出,人工神经网络的训练收敛速度很快,这也是运算时间短的原因。
上述两种方法的参数估计结果与已知假设参数十分接近,并且精度相当。极大似然估计方法对完整数据和截尾数据都是适用的,这在基于汽车质保数据的可靠性评估中更具实际意义。人工神经网络估计法运算时间短,具有速度快精度高的优点;同时,神经网络估计法的精度对经验分布函数精度的敏感性较高,通过提高经验分布函数的精度,可以进一步提高神经网络估计法的估计精度。
5 结语
为了对商用汽车的可靠性进行评估,文中对比了基于二参数威布尔分布的极大似然参数估计法和神经网络估计法,并将这两种方法应用到某商业汽车的汽车寿命数据分析中。通过实例在估计精度、计算速度和实践意义上,对这两种方法进行对比并提出建议,两种方法在数据适用性及运算速度上各具优点,精度相当。
[1]徐微,胡伟明,孙鹏.基于两参数威布尔分布的设备可靠性预测研究[J].中国工程机械学报,2013,11(2):112-116.XUWei,HUWeiming,SUN Peng.Equipment reliability prediction based on dual-parametric Weibull distribution[J].Chinese Journal of Construction Machinery,2013,11(2):112-116.(in Chinese)
[2]龚伟俊,李为相,张广明.基于威布尔分布的风速概率分布参数估计方法[J].可再生能源,2011,29(6):20-23.GONGWeijun,LIWeixiang,ZHANG Guangming.The estimation algorithm on the probabilistic distribution parameters of wind speed based on Weibull distribution[J].Renewable Energy Resources,2011,29(6):20-23.(in Chinese)
[3]于晓红,张来斌,王朝晖.基于新的威布尔分布参数估计法的设备寿命可靠性分析[J].机械强度,2007,29(6):932-936.YU Xiaohong,ZHANG Laibin,WANG Zhaohui.Reliability life analysis of the equipment based on new Weibull distribution parameter estimation method[J].Journal of Mechanical Strength,2007,29(6):932-936.(in Chinese)
[4]傅惠民,高镇同.确定威布尔分布三参数的相关系数优化法[J].航空学报,1990,11(7):323-327.FU Huimin,GAO Zhentong.An optimization method of correlation coefficient for determining a three-parameter Weibull distribution[J].Acta Aeronautica Et Astronautica Sinica,1990,11(7):323-327.(in Chinese)
[5]庄渭峰.用微机实现威布尔参数的双线性回归最小二乘估计[J].电子产品可靠性与环境试验,1999(5):2-7.ZHUANG Weifeng.The least square assessment of bilinear regression for Weibull parameters realized by microcomputer[J].Electronic Product Reliability and Environment Test,1999(5):2-7.(in Chinese)
[6]郭强.一种小子样商用飞机系统可靠性评估方法[J].噪声与振动控制,2010(1):114-117.GUO Qiang.Small sample approach for reliability evaluation of commercial aircrafts[J].Noise and Vibration Control,2010(1):114-117.(in Chinese)
[7]范英,王顺坤,晋民杰.多种数据状态下三参数Weibull分布的极大似然估计[J].机械强度,2012,34(1):53-57.FAN Ying,WANG Shunkun,JIN Minjie.Maximum likelihood estimation of three-parameterWeibull distribution in wide range of data state[J].Journal of Mechanical Strength,2012,34(1):53-57.(in Chinese)
[8]杨谋存,聂宏.三参数Weibull分布参数的极大似然估计数值解法[J].南京航空航天大学学报,2007,39(1):22-25.YANG Moucun,NIE Hong.Advanced algorithm formaximum likelihood estimation of three parameter Weibull distribution[J].Journal of Nanjing University of Aeronautics and Astronautics,2007,39(1):22-25.(in Chinese)
[9]肖伟,赵嵩正.设备可靠性与维修决策关系研究[J].机械科学与技术,2004,23(1):85-86.XIAOWei,ZHAO Songzheng.Study on the relationship between plant reliability and maintenance decision[J].Mechanical Science and Technology,2004,23(1):85-86.(in Chinese)
[10]敖长林.基于人工神经网络的拖拉机使用可靠性研究[D].沈阳:东北农业大学,2000.
[11]麻晓敏,张士杰,胡丽琴.可靠性数据威布尔分析中秩评定算法改进研究[J].核科学与工程,2007,27(2):152-155.MA Xiaomin,ZHANG Shijie,HU Liqin.An improved rank assessmentmethod forWeibull analysis of reliability data[J].Chinese Journal of Nuclear Science and Enineering,2007,27(2):152-155.(in Chinese)
[12]ZHANG Q J.Neuro Modeler Plus[CP/DK].Ottawa,ON:Carleton University,2013.

