基于Copula理论和非参数极值估计在上下游水位的相关性分析应用

赵凯鸽，袁永生，吴清娇

(河海大学理学院，江苏南京210098)

自从Sklar教授于1959年提出Copula函数的概念以来，经过诸多学者的深入研究，形成了Copula函数的基本理论，并且在各个领域得到了广泛应用，取得了丰富的研究成果。Copula不仅将经典统计学中的线性相关系数及其他相关系数与Copula函数联系起来，推导出Copula函数与相关系数的关系式，并且能有效地解决一些非线性、非对称的复杂相关性问题。Copula函数理论的核心是Sklar定理，其重要意义在于将联合分布函数与其边缘分布函数联系起来，并提供了一种由一元边缘分布构造多元联合分布函数的途径和方法，其推论给出了利用连续分布函数的伪逆函数和联合分布函数求出其相应Copula函数的方法。Copula理论是一种定性与定量分析相结合的统计分析方法。

由Copula导出的相关性度量不仅可以描述变量间的非线性、非对称相关关系，而且还可以刻画尾部的相关性。把Copula与时变相结合，构建了t-Copula模型，这一模型将Copula中的参数看成时间的某个确定函数来进行建模，这样将会减小模型假定错误所带来的偏差。由于相关结构具有相当的不确定性和复杂性，Copula参数的时变结构根本就是未知的，很多文献采用半参数模型和非参数模型，更实用、更有效、更有意义。

事实上，很多模型的边际分布是无法准确定位的，因而传统的参数估计存在一定的局限性。由于非参数估计是不需要事先知道模型的边际分布，基于此，文中运用非参数技术来估计Copula函数中的参数，从而克服了传统参数估计的不足。

在国外，Fermaniam［1］认为高维数据进行Rosenblatt变换比较困难，直接利用基于样本数据的多变量核密度估计的密度函数与均匀密度函数相比较;Werker［2］利用秩相关函数τ的演化方程确立的时变Copula模型来研究波动溢出的问题;Genest［3］利用数据的概率积分变换来估计其相应的密度模型，从而确定最优的Copula函数;Gordon和Johan对任意维下的极值Copula进行非参数估计;Gudendorf G，Segers J［4］从理论上研究了任意维数的极值Copula函数的非参数估计。

在国内，学者张尧庭［5］从理论上探讨了Copula在金融上应用的可行性;韦艳华、张世英［6］等用Copula-ARCh模型研究了上海证券市场中几个板块间的相关性;史道济，张明恒［7］等也应用Copula函数对金融市场的相关性作过一些探讨;赵丽琴、籍艳丽［8］采用对边际分布不作具体假设的非参数核密度估计Archimedean Copula的参数，并用实际说明其方法的有效性。

文中对现有的非参数估计量进行改进，克服了现有估计量的谱测度H的限制，并引进新的非参数极值估计Z—L方法，以泾流从1975年到1996年上游和下游在不同时间的水位、流量和含沙为例，给出非参数估计的具体实现过程。

1 Copula理论简介

Copula理论是由Sklar在1959年提出的。Sklar指出，可以将任意一个n维联合累积分布函数分解为n个边缘累积分布函数和一个Copula函数，其中边缘分布函数描述的是变量的分布，Copula函数描述的是变量之间的相关性。也就是说，Copula函数实际上是一类将变量联合累积分布函数同变量边缘分布函数连接起来的纽带函数，因此也有人称其为“连接函数”。

1.1 Copu la函数的定义及Sk lar定理

定义1 n维Copula函数［9］(或称为n－Copula)是一个函数C，具有如下性质:

1)定义域为 In，即［0，1］n;

2)对于任意 t=(t1，t2，…，tn)∈［0，1］n，若至少有一个tk=0，则C(t)=0;

3)C有零基面(grounded)，且是n维递增的，即对于定义域中的任意真子集

B= ［a1，b1］× ［a2，b2］× …［an，bn］有

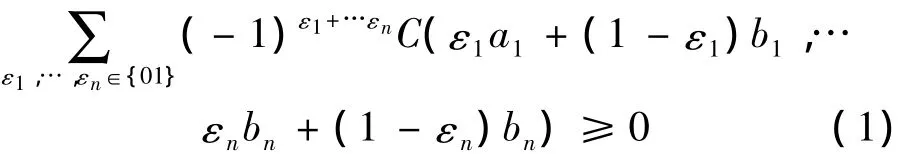
4)对于任意u∈［0，1］，C的边缘函数Ck满足

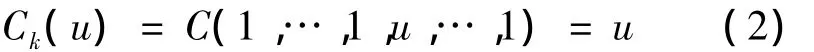
定理2(Sklar定理)Sklar定理［10］是 Copula函数理论的核心，也是基础，在统计学中的应用最为广泛，其阐明了多元分布函数与其边缘分布函数的关系。

令F是d维联合分布函数，其边缘分布F1，…，Fd，一定存在一个 d－Copula函数C，对于任意向量x=(x1，…，xd)∈ Rd，则有

如果F1，…，Fd都是连续的，则C是唯一的;否则C在Ran F1×…×Ran Fd上是唯一的。相反，如果C是一个d－Copula且F1，…，Fd是边缘分布函数，则由式(3)确定的函数是边缘分布为F1，…，Fd的d维联合分布函数。

对于有连续的边缘分布情况，对于所有的u∈［0，1］d，均有

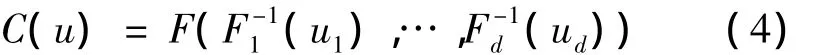
1.2 随机变量间的相关性度量

任何变量之间如果不是相互独立的，那么一定会存在一定的相关关系。几种常用的刻画多个随机变量之间的相关性度量，有线性相关系数、Kendall秩相依系数、Spearman秩相依系数、尾部相关系数等，其中Kendall秩相依系数和Spearman秩相依系数是刻画一致性的，而尾部相关系数是一个极值理论的测度，用来表示当一个观测变量的实现值为极值时，另一个变量也出现极值的概率。

相关性一直是人们关注的一个焦点问题。Nelsen指出，若对变量作单调增的变换，相应的Copula函数不变，因而由Copula函数导出的一致性和相关性测度的值也不会改变。

1.2.1 线性相关系数(Linear Correlation)(x，

y)T为一个具有非零有限方差的随机向量，则基于两个随机向量(x，y)T的线性相关系数被定义为

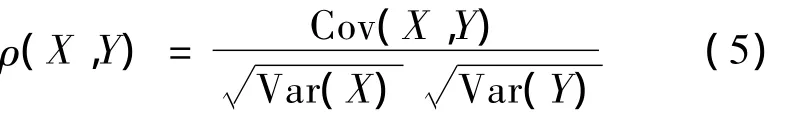
如果两个随机变量是独立的，它们的线性相关系数ρ(x，y)=0;但是反过来却并不成立。如果 |ρ(x，y)|=1，那么两个随机变量完全相关。在严格的单调递增线性变换中，线性相关系数是不变的;但在严格的单调递增的非线性变换中，相关系数却是改变的。

1.2.2 Kendall秩相依系数

因此，Kendall秩相依系数 τm［3］可以用来反应随机向量变化一致性的程度。特别地，当τm=1、τm=－1和τm=0时，分布表示X和Y变化完全一致正相关、完全一致负相关和不能确定是否相关。

1.2.3 Spearman 秩相依系数

1.2.4 尾部相关系数

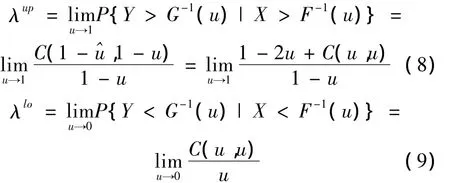
其中

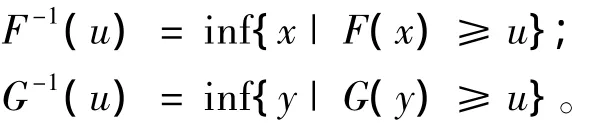
若尾部相关系数［6］λup或 λlo∈ (0，1］，则随机变量X，Y上尾或下尾相关;若λup或λlo=0，则随机变量X，Y上尾或下尾渐进独立。

在实际生活中，数据多呈现出尖峰后尾性，对尾部相关关系的分析是掌握波动变化规律以及有效控制风险的一个关键问题。而基于Copula函数的尾部相关系数包含了尾部相关的全部信息，就可以更全面、更深入地描述变量之间的相关关系。

1.3 极值Copula及其改进

在实践生活中，与极值分布函数［11］相对应的是重要的极值Copula函数簇，而对于样本最大值的广义极值分布的边缘

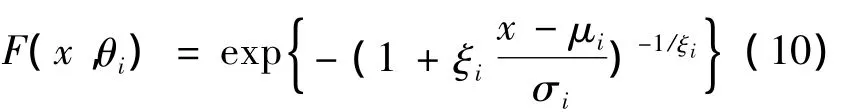
这里

是一个位置参数，σi＞0是一个尺度参数，ξi∈R是一个形状参数，它是极值指标。

假定 Sij= － ln Fj(xij)，1≤i≤n，1≤j≤ d，并且是标准的指数自由变量对于 ω ∈ Δd－1，有

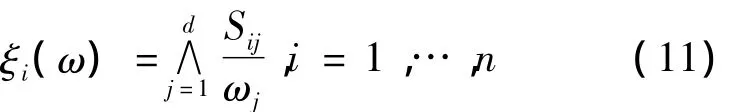
幂型方程:g(x)=xa，a ＞ 0，有

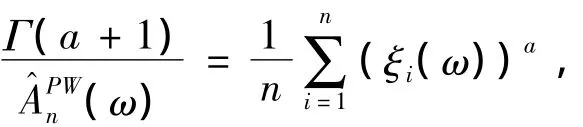
当a=1时刚好是基本的Pickands型估计量。

对数方程:g(x)=ln x，有

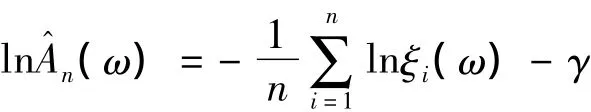
它刚好是CFG估计量。

上面两个方程满足顶点约束:A(ei)=1，…，d

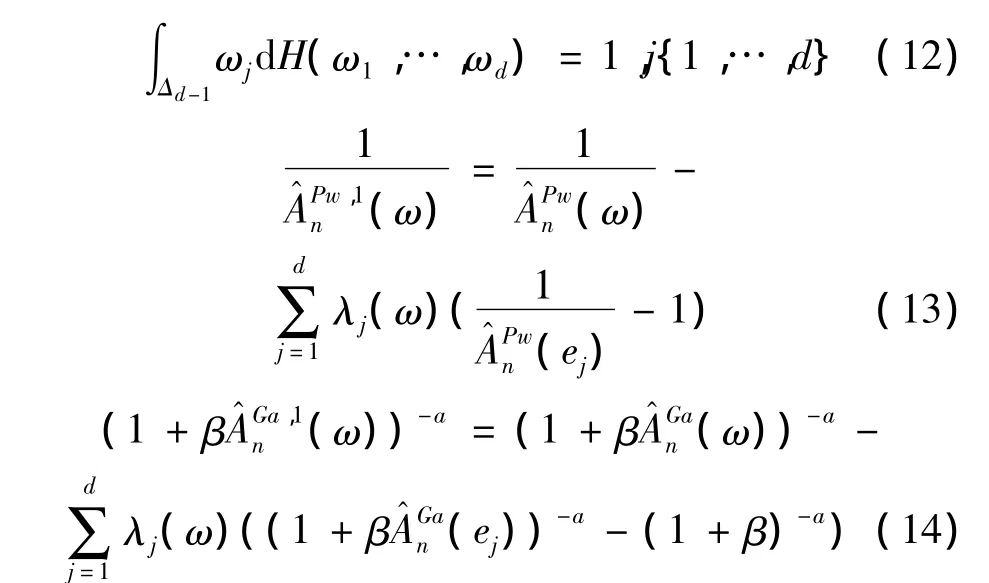
其中λj(ω):Δd－1→R上验证λj(ek)= δjk，k=1，…，d是连续函数(δjk是克罗内克δ方程)。所以有

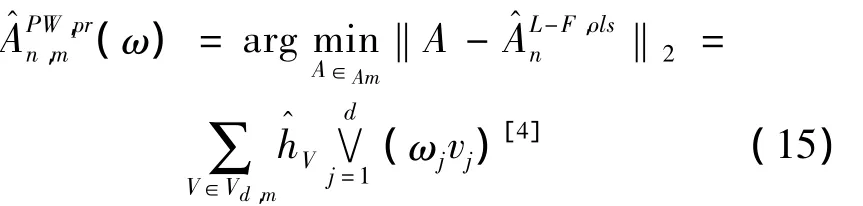
2 非参数核密度估计简介

由于上下游水位高低分布出现的“尖峰”、“厚尾”现象，很多情况下不满足正态分布。有文献采用t－GARCH来描述，还有文献采用经验分布来表述。这些方法都有合理的一面，但也有其不合理的一面。比如说，t－GARCH假设本身就是一种局限，而经验分布一般不连续，光滑性不够，用来表述上下游水位高低的分布所产生的误差较大，介于这些不利因素，现应用非参数核密度估计技术来处理上下游水位的边缘分布。

下面的结论仍然成立。

2.1 非参数核密度估计的定义及基本统计性质

设K(·)为R1上一个给定的概率密度函数，hn＞0是一个与有关的常数，满足当n→∞，hn→0，则

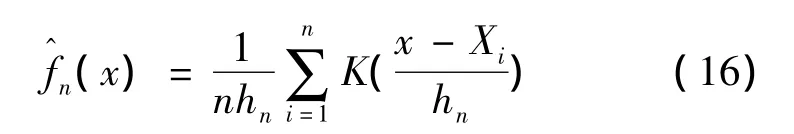
为f(x)的一个核估计，其中K(·)称为核函数，hn为窗宽或光滑参数。

定理3 若(rA，rB)在点分布函数值的估计分别为

则当核函数选取为正态核，上面两式可以表示为

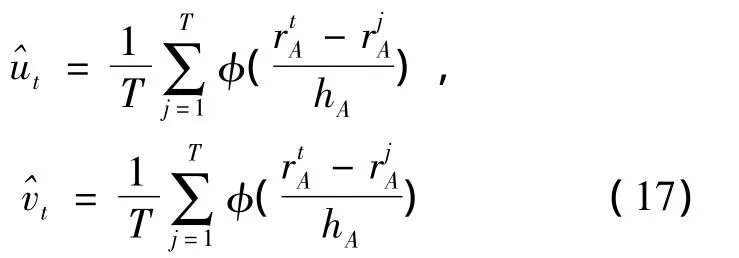
在进行非参数核密度估计时，要解决的问题是如何选择恰当的核函数及如何确定最优的光滑参数。

2.2 核函数的选择

核函数的选择［13］可以有很多种，但是在一般情况下，核函数的选择往往取决于根据距离分配各个样本点对密度贡献的不同。通常选择什么样的核函数并不是密度估计中最关键的因素，因为选用的任何核函数都能保证密度估计具有稳定相合性。最重要的是光滑参数对估计分布的光滑程度影响很大，所以选择什么样的光滑参数是很重要的。

2.3 光滑参数的选取

由式(17)可知，核密度估计的应用需要决定光滑参数hn，而分布密度函数是连续的，所以由的均方误差(MISE)，即MISE的最小来确定hn。由极值定理，解

可得到hn的一个最使满意的解:

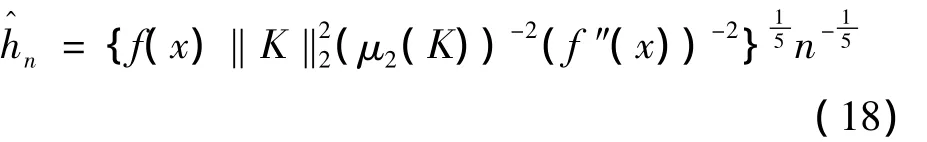
其中

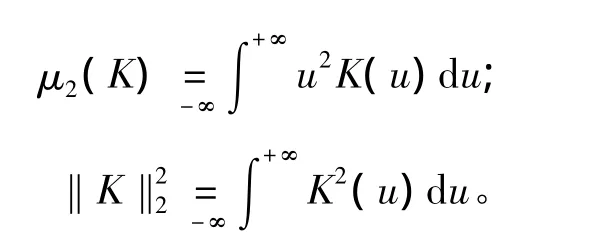
通常使用经验法则决定光滑参数，假设f(x)为正态概率密度N(0，σ2)，若核函数选取为正态核，则有

3 时变Copula模型的非参数极值估Z－L计算法

设有时间序列{(Xi，Yi)，t=1，2，…，T}，单变量随机时间序列{Xi}和{Yi}都是平稳的，现对{Xi}和{Yi}之间的联合分布或相关结构进行建模，根据时变Copula模型的非参数估计思路，得出算法:

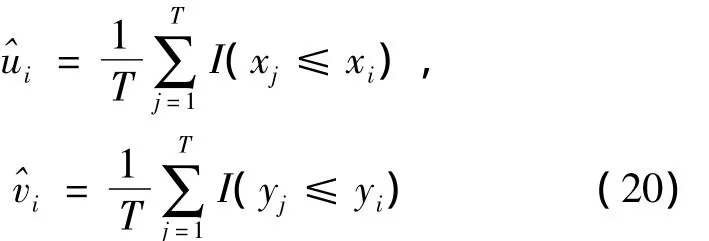
其中I(·)是示性函数。

其次，确定最佳光滑参数［14］，也就是给定光滑参数的可能取值集合，比如{h1，h2，…，hm};然后对光滑参数的每一个可能取值 hi，i=1，2，…，m，在伪样本观测条件下根据下式:

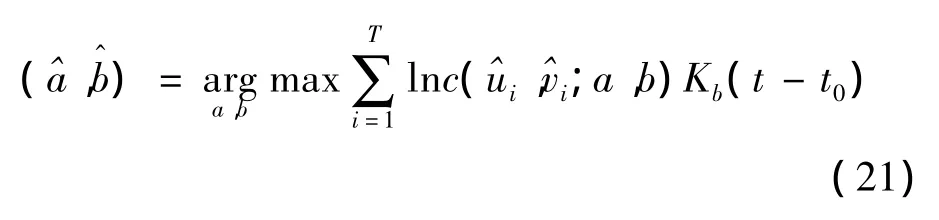
其中核函数选取

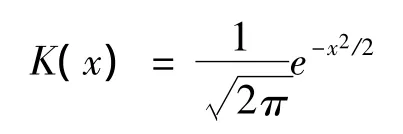
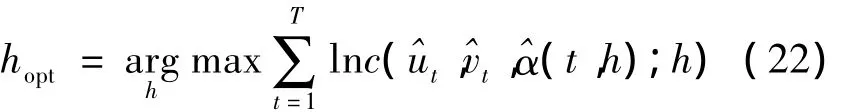
最后，时变Copula模型的非参数极值Z－L估计:

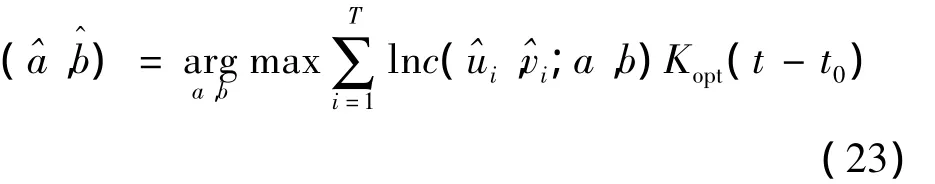
由式(23)就可以得到时变Copula模型的时间点t0的参数估计量(t0)=，再将此过程对每一个时间点进行循环，就得到时变Copula模型参数估计量的时变轨迹。

4 径流上下游水位的相关性

文中数据包括1975年至1996年夹河滩水位和高村水位，共计497个调查数据。首先用核方法来估计密度函数，核估计主要是由核密度函数和窗宽构成。水位的变化率定义为:Xt=10(ln Pt－ lnt－1)，再选取高斯核函数

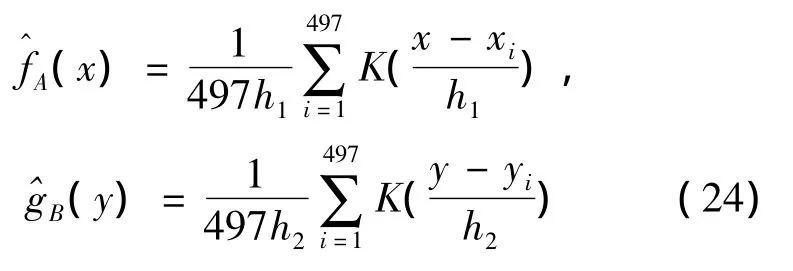
从图1a，b可以看出，整个分布略显左偏，表现出一定的间峰程度。夹河滩和高村的水位变化具有很强的厚尾性，且两者间的变化存在一定的相关性，这和实际生活中的情况是一致的。下面观察水位变化率序列的统计特征，其结果如表1所示。

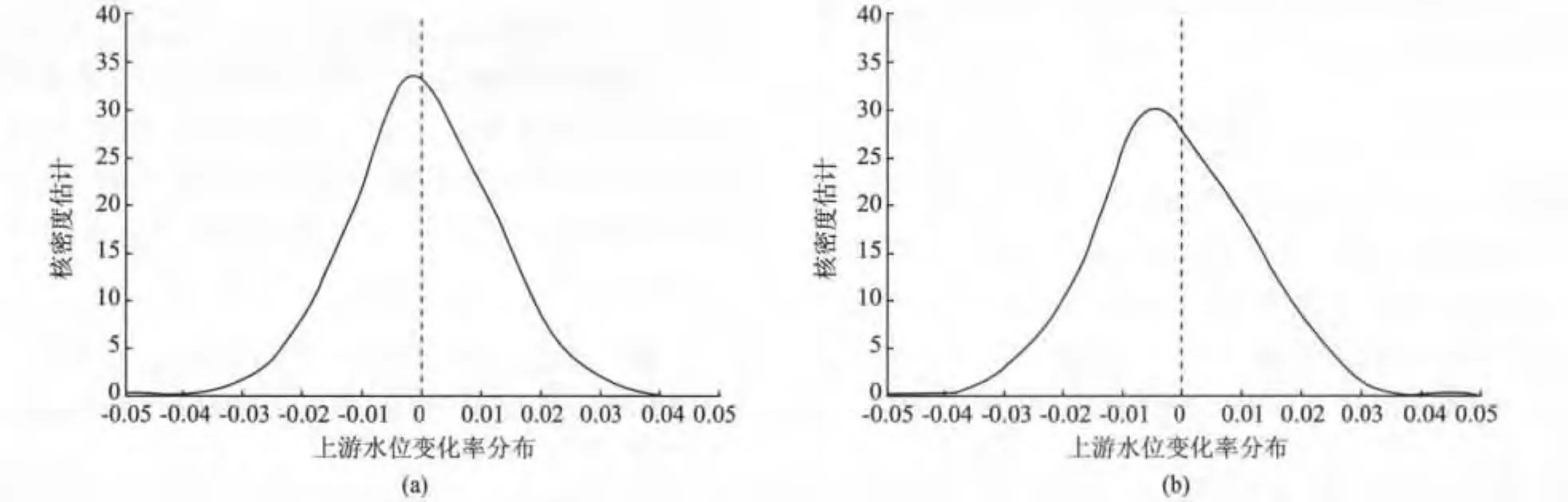
图1 夹河滩和高村水位的边际密度的核估计Fig.1 Nuclear estimate of the C lip quay’s and the High village’smarginal density

表1 上游、下游水位序列的基本统计Tab.1 Basic statistics of upstream and downstream’s water level sequences

由表1数据可以知道，上游和下游水位的均值和标准差都大于0，高村的峰度比较大，这即是经常说的尖峰厚尾特征。负的偏度表明在整个调查期间，水位下降的天数少于上升的天数，每天上升的平均幅度高于每天下降的幅度。高的峰度表明水位以更大的概率出现在各自的均值附近。

图2a，b分别给出上游夹河滩和下游高村的水位变化率的时间序列。可以看出，它们之间的波动有一定的相似性，这说明上游、下游水位的变化有一定的联系。

还求得相应的相关系数如下:Linear Correlation 0.735 36;Kendallτm0.914 83;Spearman ρk0.907 35;尾部相关系数0.886 21。数据说明上游夹河滩和下游高村的水位存在着较强的相关性，且ρk和τm比经典的相关系数大，可见运用非参数核密度估计得到的Copula函数参数值是非常准确的。

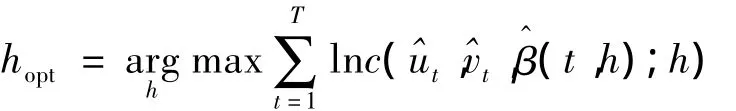
通过公式计算得到夹河滩、高村水位样本的Kendalls秩相关系数，其值非常接近1，说明夹河滩和高村的水位具有极高的正相关性，与实际情况相符。同时也说明文中所估计的Copula是合理的，非参数极值估计Z－L算法在Copula函数的估计问题上是可行的。

表2 参数估计Tab.2 Parameter estimation

因此，非参数估计Copula密度函数在其度量模型相关方面是有意义的，并且在研究实际问题时，利用非参数估计相依模型间的联系是很有效的，它也能够避免由于失当的模型或参数的选择所产生的误差。

致谢:东南大学数学系林金官教授所作关于《链接函数的非参数极值估计》的报告，对本文帮助很大，仅此致谢!

［1］Jean-David Fermanian J.Goodness-of-fit tests for Copulas［J］.Journal of Multivariate Analysis，2005，95(1):119-152.

［2］Rob W J，van den Goorbergh，Christian Genest，et al.Bivariate option pricing using dynamic copula models［J］.Insurance:Mathematicsand Economics，2005，37:101-114.

［3］Genest C J，Quessy F，Remillard B.Goodness-of-fit procedures for copulamodels based on the probability integral transform［J］.Scandinavian Journal of Statistics，2006，33(2):337-366.

［4］Gudendorf G，Segers J.Nonparametric estimation of an extreme-value copula in arbitrary dimensions［J］.Journal of Multivariate Analysis，2011，102(1):37-47.

［5］张尧庭.连接函数(Copula)技术与金融风险分析［J］.统计研究，2002(4):48-51.ZHANG Tingyao.Copula technique and risk analysis［J］.Journal of Northwest Statistical Research，2002(4):48-51.(in Chinese)

［6］韦艳华，张世英，孟利峰.Copula理论在金融上的应用［J］.西北农林科技大学学报:社会科学版，2003，3(5):97-101.WEIYanhua，ZHANG Shiying，MENG Lifeng.The application of Copula in the financial［J］.Journal of Northwest Sci-Tech University of Agriculture and Forestry:Social Science Edition，2003，3(5):97-101.(in Chinese)

［7］张明恒.多金融资产风险价值的Copula计量方法研究［J］.数量经济技术经济研究，2004(4):29-32.ZHANG Lingheng.Many financial assets value at risk of copulasmeasurementmethod research［J］.Quantitative and Technica Economics，2004(4):29-32.(in Chinese)

［8］赵丽琴，籍艳丽.Copula函数的非参数核密度估计［J］.统计与决策，2009(9):29-32.ZHAO Liqin，JI Yanli.Copula and nonparametric kernel density estimation［J］.Statistics and Decision，2009(9):29-32.(in Chinese)

［9］Nelsen R B.An Introduction to Copulas［M］.2nd ed.New York:Springer Science Business Media，2006:7-19，157-215.

［10］Capéraà P，Fougères A L，Genest C.A nonparametric estimation procedure for bivariate extreme value copulas［J］.Biometrika，1997，84(3):567-577.

［11］Bücher A，Dette H，Volgushev S.New estimators of the Pickands dependence function and a test for extreme-value dependence［J］.The Annals of Statistics，2011，39(4):1963-2006.

［12］Prakasa Rao B L S.Nonparametric Function Estimation［M］.London:Academic Press Inc，1983.

［13］ ZHANG D，Wells M T，PENG L.Nonparametric estimation of the dependence function for a multivariate extreme evalue distributions［J］.Journal of Multivariate Analysis，2008，99(4):577-588.

［14］龚金国，史代敏.时变Copula模型非参数估计的大样本性质［J］.浙江大学学报:理学版，2012，39(6):630-642.GONG Jinguo，SHIDaimin.Large sample properties of nonparametric estimation in time-varying Copula model［J］.Journal of Zhejiang University:Science Edition，2012，39(6):630-642.(in Chinese)

［15］龚金国.Copula与非参数核密度估计［D］.成都:四川大学，2005.