一类非局部边值条件抛物型方程组解的性质

吴春晨

(福州大学至诚学院，福建 福州350002)

文中考虑以下非线性抛物型方程组

其中，m，n，h ＞ 1，a，b，c，p，q，r ＞ 0 为常数，Ω 为RN(N≥1)中的有界区域，具有光滑的边界∂Ω，η1(x，y)，η2(x，y)，η3(x，y)≠0 是对于定义在 x∈∂Ω，y∈上的非负连续函数，其中(u0，z0，w0)为正的连续函数并满足以下相容性条件:

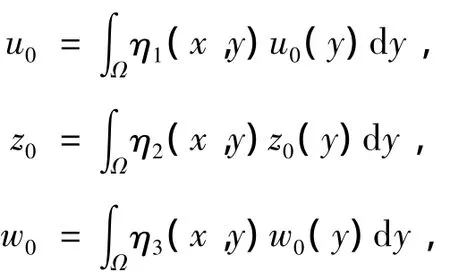
其中，x∈ ∂Ω。

近些年来，许多研究者都致力于探讨带非线性边界条件的方程组解的性质，在热弹性力学理论中许多重要的物理现象在模型上可以由非线性耦合的抛物型方程组描述［1－3］。Yongsheng MI等［3］讨论了方程组

受此启发，文中在与其相同的边界条件与初始条件下，改变动力项，并把方程扩展为3个，即为(Ⅰ)，关于相同的动力项笔者已做系列研究［4－6］，文中，式(Ⅰ)的解(u，z，w)表示3种混合材料的温度。

1 预备知识和定理

记 QT= Ω × (0，T)，

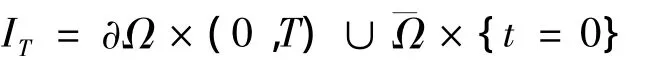
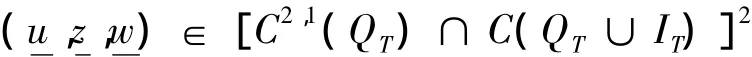
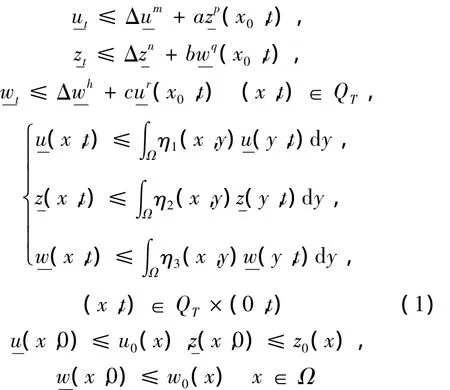
满足如果将式(1)中的“＜”全部改为“＞”，则可得到式(Ⅰ)的一个上解的定义。比较原理 若为式(Ⅰ)在x∈中的一个非负上解和非负下解，且

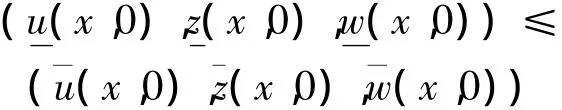
则在QT中，如果

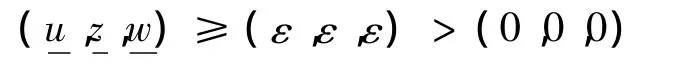
或

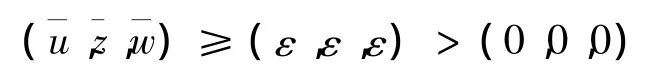
证明方法与文献［7］相同，故略。主要结论为

定理1 设

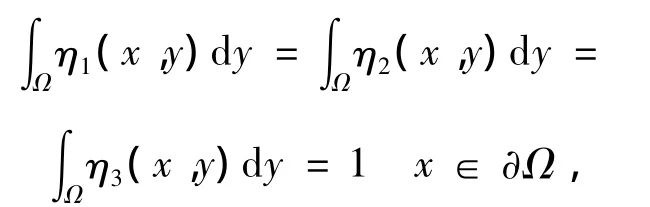
则当pqr≤1，式(Ⅰ)存在整体解;当 pqr＞1，式(Ⅰ)的解在有限时刻爆破。

定理2 设

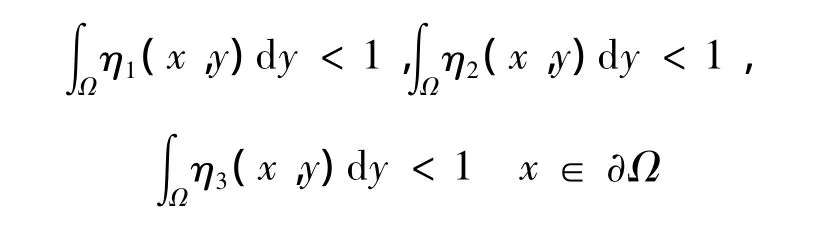
1)如果pqr＜mnh，则式(Ⅰ)存在整体解;

2)如果 pqr=mnh，则当 a，b，c充分小时，式(Ⅰ)存在整体解;

3)如果p，q，r ＞ 1并且pqr ＞ mnh，则当(u0，z0，w0)或者a，b，c充分小时，式(Ⅰ)存在整体解，如果(u0，z0，w0)足够大，式(Ⅰ)的解会在有限时刻爆破。

2 整体存在性和爆破的证明

定理1证明 令(f，g，j)是以下常微分方程组的唯一解:

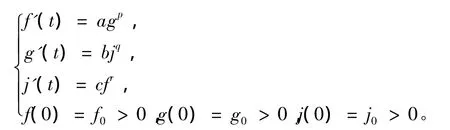
众所周知，当且仅当pqr≤1，对某些正的初值(f0，g0，j0)，(f，g，j)会整体存在。如果取

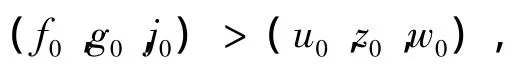
则(f0，g0，j0)为式(Ⅰ)的一个上解，由于

注意到

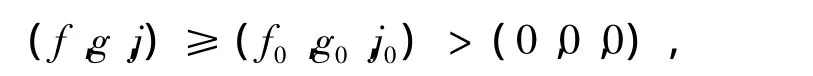
由比较原理知

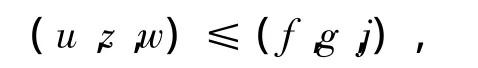
于是，当 pqr≤ 1，(u，z，w)整体存在。另外，如果取

则(f，g，j)为式(Ⅰ)的一个下解，且

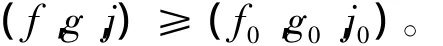
由比较原理，有

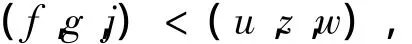
则对pqr＞ 1，(u，z，w)在有限时刻爆破，证毕。

定理2证明 令V(x)是在线性椭圆问题下唯一的正解:

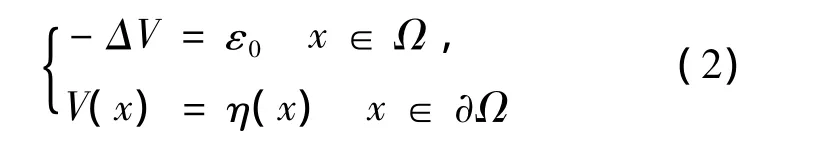
其中

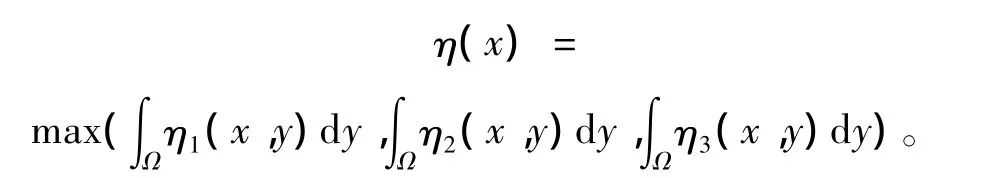
选取

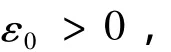
使得

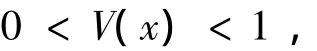
由于0＜η(x)＜1，这样的ε0会存在。令

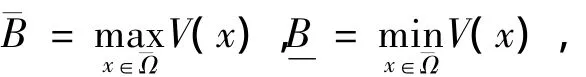
定义向量值函数

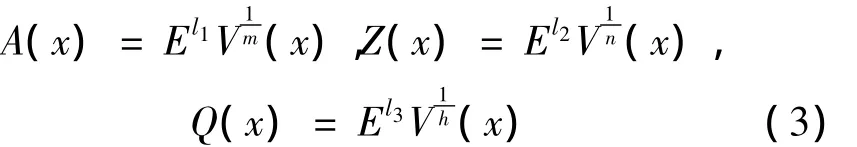
其中，E，l1，l2，l3＞ 0 待定，则有

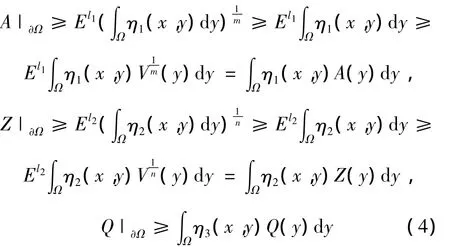
另一方面，

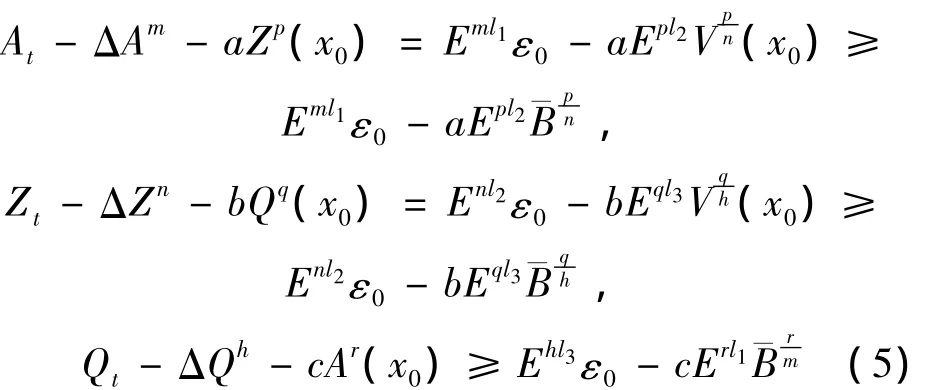
1)对于pqr＜mnh的情况，选取l1，l2＞0，l3＞0，使得

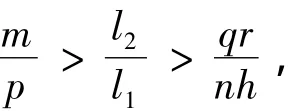
且

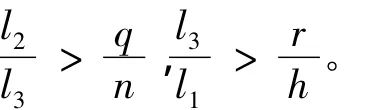
联立式(4)和式(5)，取

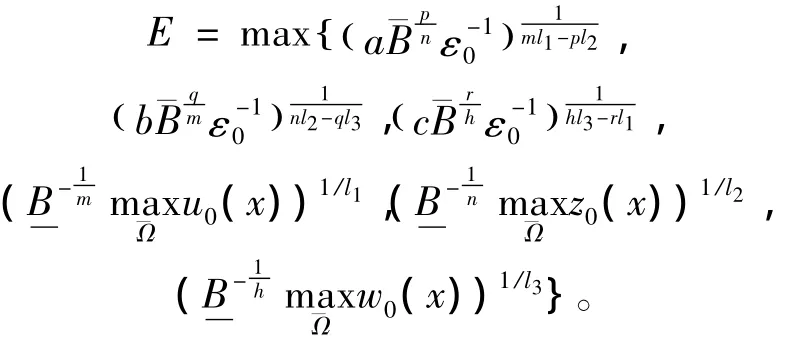
则定义在式(3)的(A，Q，Z)是式(Ⅰ)的一个上解，并且

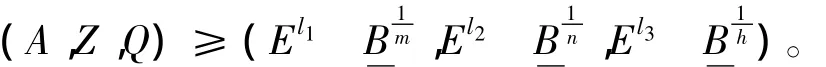
由比较原理知，(u，z，w)≤ (A，Z，Q)，因此(u，z，w)整体存在。

2)对于pqr=mnh的情况，选取l1，l2＞ 0，l3＞0，使得

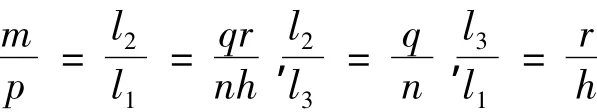
则对于任意给定的(u0，z0，w0)，选取充分大的E ＞0，使得

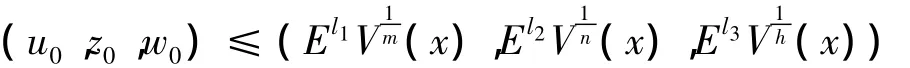
设

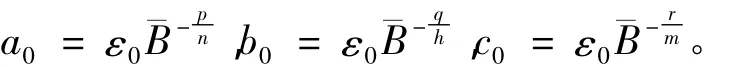
易于验证，在 a ≤ a0，b≤ b0，c≤ c0时，(A，Q，Z)是式(Ⅰ)的一个上解。因此，由比较原理得(u，z，w)整体存在。

3)就pqr＞mnh而言，对于不同的初始值有两种不同的结果。对于整体存在部分，相似于1)和2)的证明，首先，选取 l1，l2＞ 0，l3＞ 0，使得

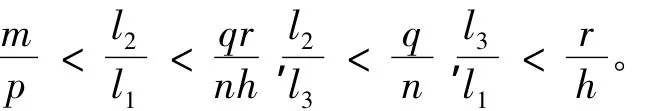
对于任意 a，b，c ＞ 0，

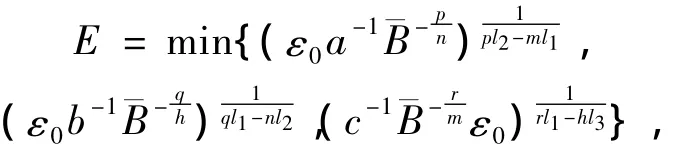
则当

时，(A，Q，Z)是式(Ⅰ)的一个上解，由比较原理知，对于(u0，z0，w0)满足式(6)，(u，z，w)整体存在。

另一方面，对于任意给定的初始值(u0，z0，w0)，存在适当大的常数E＞0，使得

对于这样的一个固定的E，设

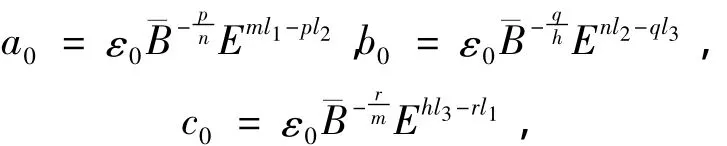
则在 a≤ a0，b≤ b0，c≤ c0时，(A，Q，Z)是式(Ⅰ)的一个上解。由比较原理知，(u，z，w)整体存在。

为了证明爆破部分，考虑以下多孔介质问题:

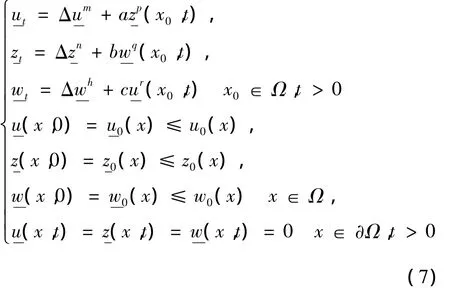
定理2证毕。

［1］LIHuiling.The blow-up property of positive solutions for a nonlinear parabolic equation［J］.Science in China(Series A):2007，37(3):257-273.

［2］陈玉娟.非局部退化拟线性抛物型方程组解的爆破和整体存在性［J］.数学物理学报，2011，30A(2):386-396.CHEN Yujuan.Blow-up and global existence for a nonlocal degenerate quasilinear parabolic system［J］.Acta Mathematica Scientia，2010，30A(2):386-396.(in Chinese)

［3］MIYongsheng，MU Chunlai.A degenerate parabolic system with localized sources and nonlocal boundary condition［J］.Front Math China，2012，7(1):97-116.

［4］吴春晨.一类非线性抛物型方程组正解的爆破［J］.山西大同大学学报:自然科学版，2012，23(3):5-7.WU Chunchen.The blow-up property of positive solutions for a nonlinear parabolic system［J］.Journal of Shanxi Datong University:Natural Science Edition，2012，23(3):5-7.(in Chinese)

［5］吴春晨.一类交叉耦合抛物型方程组正解的爆破性质［J］.福建工程学院学报，2012，10(6):7-10.WU Chunchen.The blow-up property of positive solutions to a class of nonlinear parabolic equations with cross-coupling［J］.Journal of FuJian University of Technology，2012，10(6):7-10.(in Chinese)

［6］WU Chunchen.Blow-up and global existence for a quasilinear parabolic system［J］.Discrete Dynamics in Nature and Society，2014，2014:1-4.

［7］Anderson JR.Local existence and uniqueness of degenerate parabolic equations［J］.Comm Partial Differetial Equations，1996，16:105-143.

［8］DU L L.Blow-up for a degenerate reaction-diffusion system with nonlinear localized sources［J］.JMath Anal Appl，2006，324:304-320.