MQ函数和M atern函数在LM APS方法中的比较

杨海婷， 张学莹

(河海大学理学院，江苏 南京210098)

近年来，无网格方法在计算偏微分方程数值解方面发展迅速，当遇到网格划分困难、网格突变以及网格移动等问题时，无网格方法具有明显的优势。

全局配点型 RBFs方法［1－2］是一种真正意义上的无网格方法，它成功地克服了上述困难，但是采用它求解偏微分方程时随着插值节点数的增加，系数矩阵的条件数增大，容易导致系数阵奇异，满秩甚至病态，这给处理大规模的问题带来不便。为了改进这些问题，文献［3－5］采用局部径向基函数节点插值法减少了矩阵的病态性。之后，CHEN C S等人采用LMQ思想，在近似特别解(Method of Approximate Particular Solution，MAPS)［6］的基础上提出了局部近似特别解法(简称 LMAPS)［7］。LMAPS方法具有MAPS和RBFs的优点，它不仅规避了全局矩阵的病态和满秩，而且可以用较少的节点数获得更高的精度。目前，LMAPS方法已经取得了很大的发展并广泛应用于物理领域。

文中介绍了MQ函数中形参c的优化方法，分别选取MQ函数和Matern函数作为LMAPS方法中的径向基函数，并将这两种函数应用到规则区域和不规则区域上的偏微分方程进行数值求解，同时给出相应的误差比较分析。

1 LMAPS方法的基本理论

1.1 控制方程

考虑偏微分方程

其中，λ，a，b，c是给定的常数，Δ是二阶线性Laplace算子，B 是边界算子，f(x，y)，g(x，y)和 u0是给定的函数。

1.2 LM APS方法的基本理论

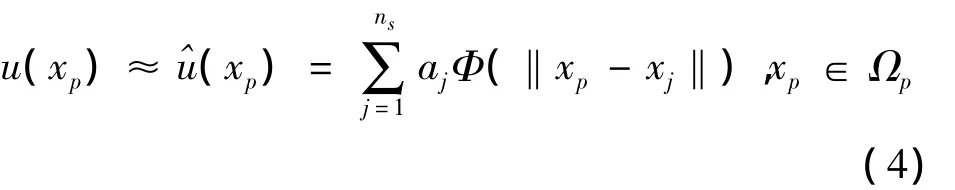
这里‖·‖是欧几里得范数，φ是径向基函数。

此处

并且

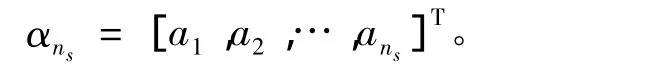
由于局部支撑域内各插值节点相异，从而矩阵Φns可逆，故有

对于∀xp∈Ω，将方程(1)在空间上离散得到

其中

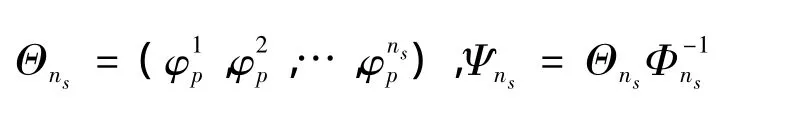
并且

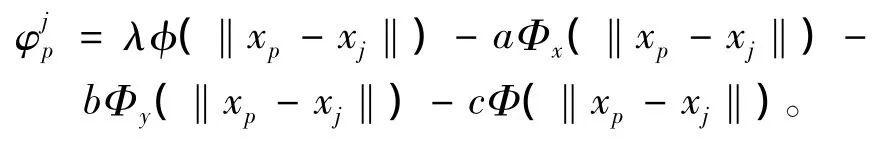
通过在适当位置添加零元素将向量Ψns延拓成n维向量 Ψn［7］，则有

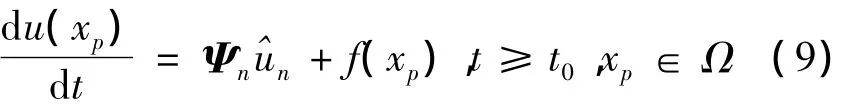
1.3 MQ函数和M atern函数

局部近似特别解方法是一种基于RBFs的无网格方法，用它求解偏微分方程得到的数值解的精度很大程度上取决于基函数。MQ函数具有收敛速度快、插值精度高的特点，而相比MQ函数，Matern函数插值的LMAPS方法则省去了调节形参c的时间，在降低计算量的基础上提高了计算效率。文中选取MQ函数和Matern函数作为LMAPS方法中的基函数，并根据数值结果进行误差比较分析。这里采用MQ函数的一般形式:

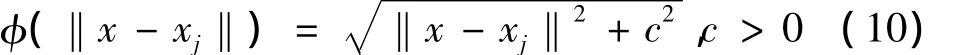
其中，x=(x，y)表示在物理空间上支撑域内点的坐标，c是形状参数，对方程(5)求积分［8-9］可得

其中，r= ‖x－xj‖。

如果选取Matern函数作为基函数有

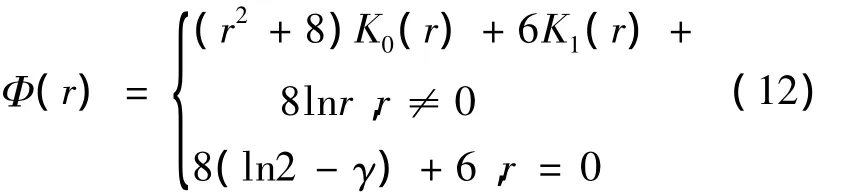
其中，ΔΦ =r2K2(r)，γ是欧拉常数，K0(r)和K1(r)分别是0阶和1阶第二类贝塞尔函数。

1.4 形参c的优化方法

由于形参c的选取直接影响基于MQ函数插值的LMAPS方法的近似精度，传统意义下，通过不断尝试不同的形参c［10］或者一些特殊的方法，比如说，Contour Pade’算法［11］来规避系数阵的病态或满秩从而得到一个合适的形参。但是这些方法都增加了计算成本，降低了计算效率并且给处理大规模问题带来诸多不便。

为了寻找最优形参c，并且平衡用MQ函数作为基函数的LMAPS方法求解PDEs得到的数值解的精确性和稳定性，这里采用以分析交叉验证(Leave－One－Out Cross Validation，LOOCV)［12］方法为理论基础的Rippa LOOCV算法来解决离散数据插值问题中形参c的优化以及局部支撑域内ns的选取问题［12-13］。

2 数值算例

为了比较MQ函数和Matern函数在LMAPS方法中的近似精度，采用基于这两种函数的LMAPS方法求解不规则区域和规则区域上的偏微分方程，并给出误差分析。求解过程中选取kd－tree算法进行局部区域相邻节点的搜索，并分别通过Rippa LOOCV算法以及不断调试形参c来提高计算的近似精度和计算效率。最大绝对误差(MAE)、最大相对误差(MRE)、均方根误差(RMSE)定义如下:

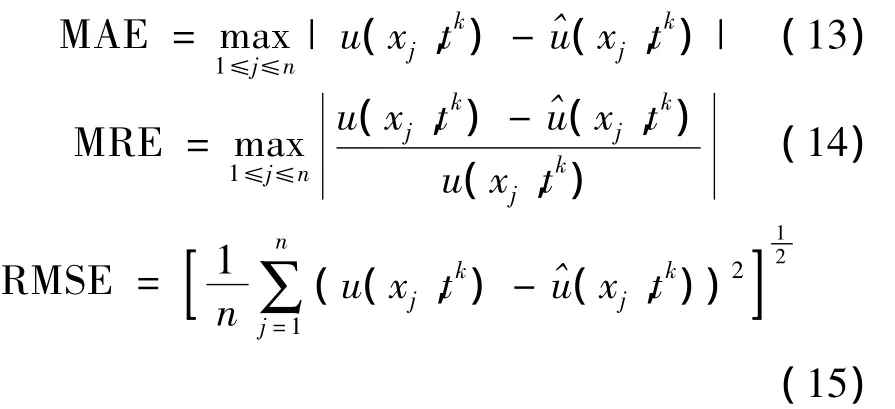
其中，n是总节点数，k是时间层，^u(xj，tk)和 u(xj，tk)分别表示k时间层上的数值解和精确解。

这里选取常见于静电学、机械工程等物理领域的Possion方程以及被用来解决激波、浅水波、交通流动力学等物理问题的Burgers′方程作为数值算例来验证上述两种函数的有效性。

算例1 考虑不规则区域下不规则点分布的二维Possion方程其边界是一个不规则区域，计算区域如图1所示。

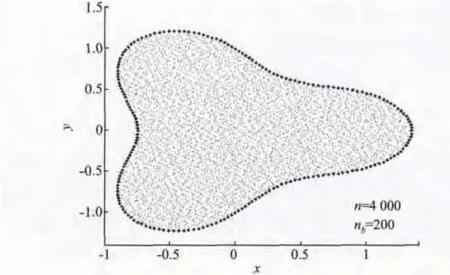
图1 n=4 000，nb=200时不规则区域下节点不均匀分布的Possion问题的计算区域Fig.1 Computational domain and distribution of the interior and boundary points with n=4 000，nb=200

图2 是总节点数n=4 000，边界点数nb=200时，优化形参c后的MQ函数和Matern函数作为基函数得到的相对误差对比图。可以看出，这两种函数的计算精度都比较满意，在整个不规则计算区域上得到的误差基本一致，并且都是平滑下降的。相比MQ函数，Matern函数在不规则边界各角处的误差出现了轻微的波动现象。

图2 n=4 000，nb=200时MQ和Matern函数得到的相对误差比较Fig.2 Profile of RAE using MQ and Matern with n=4 000，nb=200

表1为nb=200，n不同时，MQ和Matern函数得到的误差结果。一般而言，n越多，网格划分越密，所得的数值解精度越高，但实际并非如此。与MQ函数相反，随着n的增大，Matern函数取得的误差不断增大，当增大到某个特定值时，MQ函数得到的误差产生了较大的波动并出现了增大趋势。这说明误差不仅与总节点数目n有关，还与节点分布有着密切的关系。

总的来说，在处理不规则点不均匀分布问题时，优化形参c后的MQ函数得到的数值结果相比LMAPS－Matern方法具有更高的计算精度和计算效率。但是在总节点数n增大到一定程度条件下，此时从数值解的稳定性上来看，Matern函数相比MQ函数更有优势。

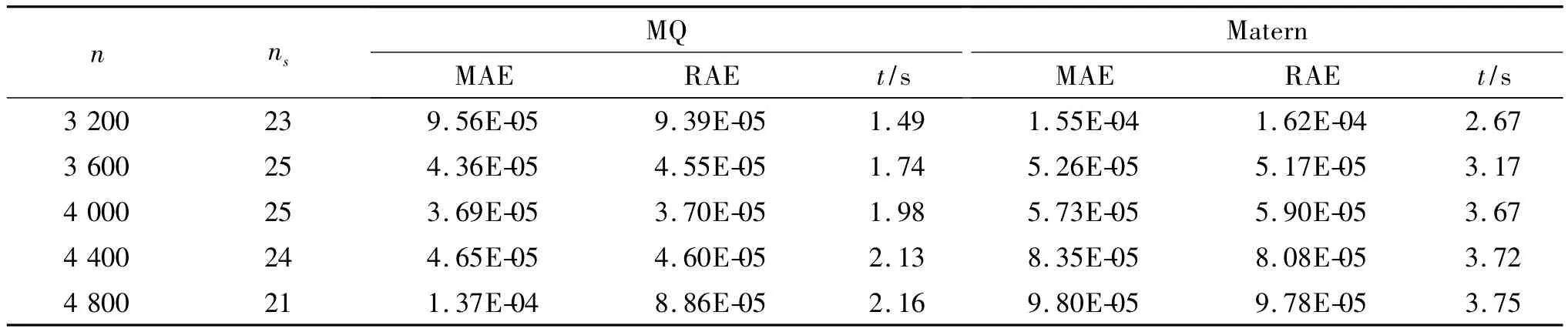
表1 MQ和Matern函数在不同n时数值结果的误差对比Tab.1 Errors and com putational time versus nusing MQ and Matern

算例2 考虑二维不定常Burgers′方程组:

其中，Ω ∪ ∂Ω = ［0，1］2，0 ＜ t＜ + ∞，方程的精确解［14］ 为

图3，4 是在 n=441，Re=100，Δt=10－3的条件下，t分别取t=0，t=1，t=2时的数值解图像。由图可见，MQ函数和Matern函数求得的数值结果基本一致，随着时间的增大，数值解的梯度变大，解的不连续性增强。此外，与v相反，得到的u的数值解的不连续区域在时间t的推动下逐渐向坐标中心移动。

图3 n=441，Re=100，c=50时MQ函数在不同时刻得到的数值结果Fig.3 uand v distributions obtained by MQ with n=441，Re=100，c=50 at different time

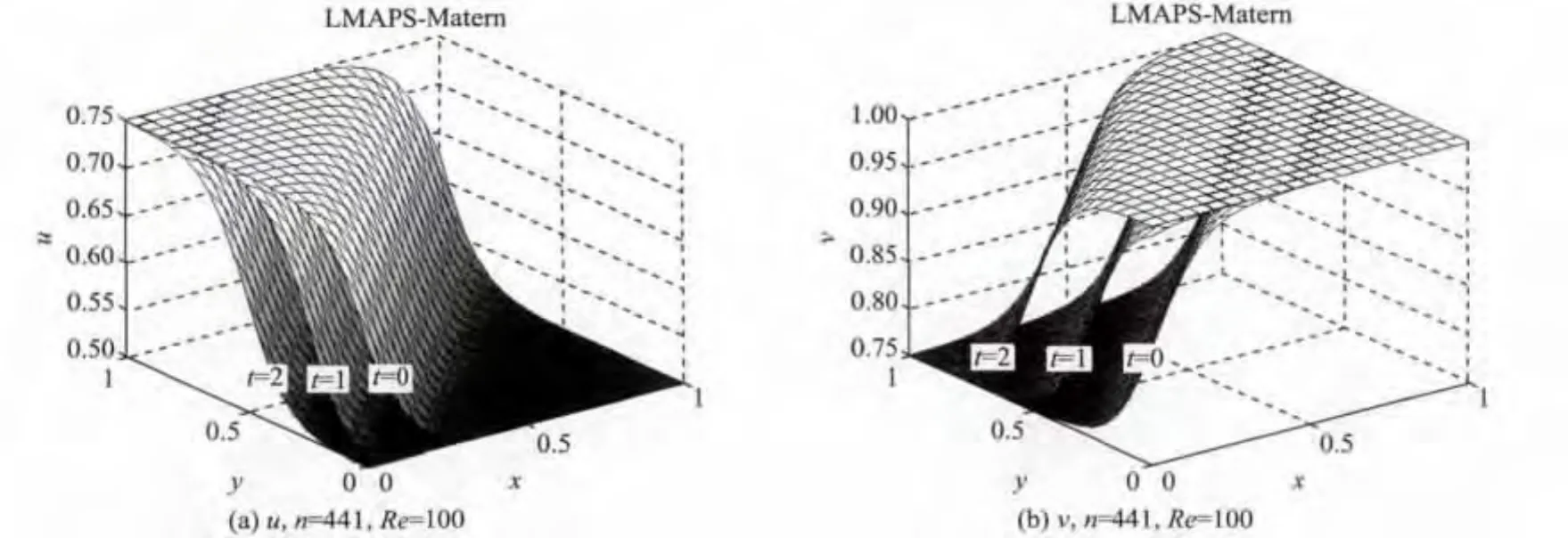
图4 n=441，Re=100时M atern函数在不同时刻得到的数值结果Fig.4 uand v distributions obtained by Matern with n=441，Re=100 at different time

表 2，3 是 Δt=10－4，t=0.1 时，两种函数得到的误差。数值结果表明它们都达到了相似的近似精度，并且随着Re的增大，误差均明显增大，当Re增大到某一特定值时，相比MQ函数，Matern函数得到了更精确的结果。同时随着总节点数的不断增多， Matern函数的优势也更加明显。

表2 t=0.1时MQ函数的误差结果Tab.2 Obtained error by MQ for example 2 at t=0.1

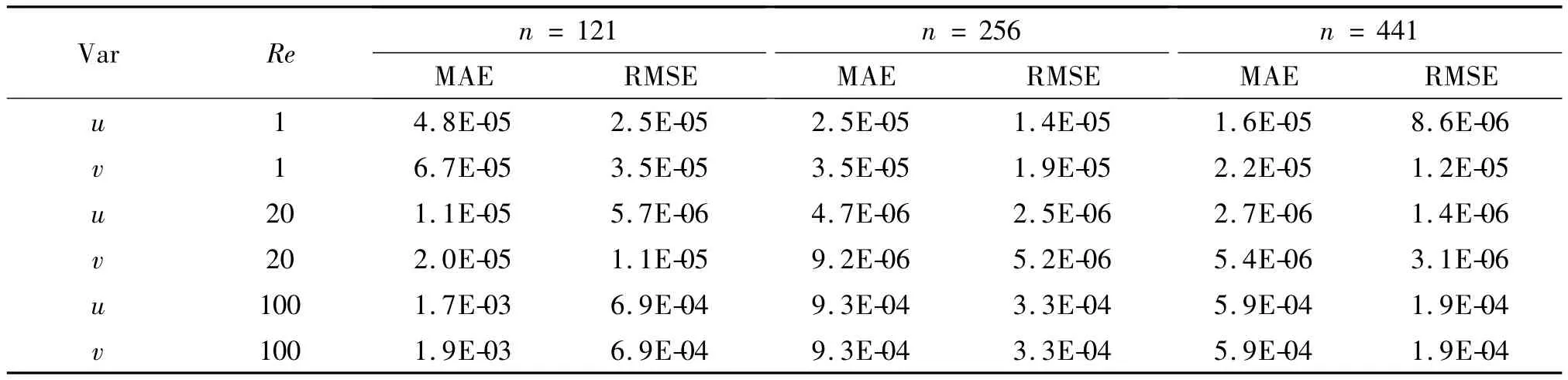
表3 t=0.1时Matern函数的误差结果Tab.3 Obtained error by Matern for example 2 at t=0.1

结合图3，4，在图5中可以看出，随着Re的增大，在数值解梯度较大的区域，这两种函数取得的绝对误差相比光滑的区域要大得多，并且误差图像出现了不同层次的波动。当Re达到100时，Burgers′方程接近半双曲型，此时用这两种函数作为径向基函数的LMAPS方法都不能得到稳定的数值解;但是相比MQ函数，Matern函数得到了较高的精度以及较小的波动。总的来说，无论从近似精度还是计算效率上来看，Matern函数对于求解规则区域上多个变量的半双曲型偏微分方程更有优势。

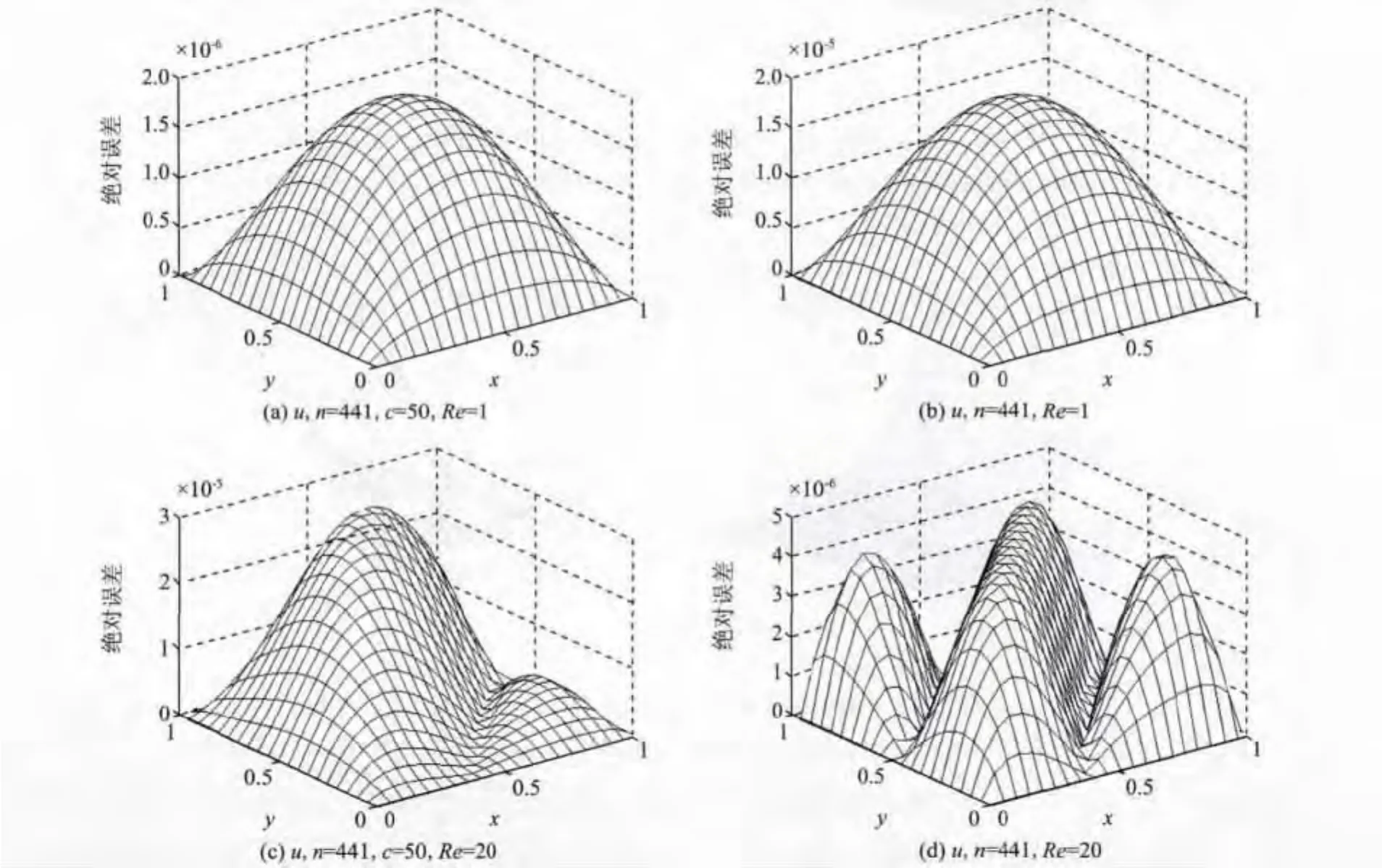
图5 n=441，t=0.2时MQ和M atern函数在不同下的绝对误差比较Fig.5 Comparison of the error p rofiles of uobtained by MQ and Matern with n=441，t=0.2

3 结语

介绍了基于径向基函数插值的无网格LMAPS方法，分别选取MQ函数和Matern函数作为基函数，并利用局部配点法构造低阶线性方程组进行插值近似来避免全局矩阵的病态和满秩。文中选取不规则区域上的Possion问题，采用优化形参c后MQ函数与Matern函数进行误差比较，同时选取规则区域上的二维Burgers′方程作为算例，并给出相应的误差分析。

数值实验表明这两种函数都取得了较高的精度，由于避免了形参c的选取，优化形参c后MQ函数相比Matern函数得到更高的近似精度和计算效率。而无论是求解不规则区域点不均匀分布问题还是高维半双曲型的偏微分方程，Matern函数得到的数值解都有着更强的稳定性。

［1］Kansa E J.Multiquadrics－a scattered data approximation scheme with applications to comutational fluid－dynamics.I.surface approximations and partial derivative estimates［J］.Comput Math Appl，1990，19:127－145.

［2］Kansa E J.Multiquadrics－a scattered data approximation scheme with applications to comutational fluid－dynamics.II.solutions to parabolic，hyperbolic and elliptic partial differential equations［J］.Comput Math Appl，2000，39:123－137.

［3］Wendland H.Piecewise polynomial，positive definite and compactly supported radial basis functions ofminimal degree［J］.Adv Comput Math，1995，4(1):389－396.

［4］WU Z.Multivariate compactly supported positive definite radial functions［J］.Adv ComputMath，1995，4(1):283－292.

［5］Vertnik R，Sarler B.Meshless local radial basis function collocation method for convective－diffusive solid－liquid phase change problems［J］.International Journal of Numerical Methods for Heat and Fluid Flow，2006，16:617－640.

［6］CHEN C S，FAN C M，WEN P H.The method of particular solutions for solving certain partial differential equations［J］.Numerical Methods of Partial Differential Equations，2012，28:506－522.

［7］YAO GM，CHEN CS，Kolibal J.A localized approach for themethod of approximate particular solutions［J］.ComputMath Appl，2011，61:2376－2387.

［8］SHU C，DING H，Yeo K S.Local radial basis function－based differential quadrature method and its application to solve twodimensional incompressible Navier－Stokes equations［J］.Computer Methods in Applied Mechanics and Engineering，2003，192:941－954.

［9］CHEN C S，FAN CM，WEN PH.Themethod of particular solutions for solving elliptic problems with variable coefficients［J］.International Journal of Computational Methods，2011，8:545－559.

［10］Kansa E J，Carlson R E.Improved accuracy of multiquadric interpolation using variable shape parameters［J］.Comput Math Appl，1992，24:99－120.

［11］Bengrt F，WrightG.Stable computation ofmultiquadric interpolants for all values of the shape parameter［J］.ComputMath Appl，2004，47:497－523.

［12］Rippa S.An algorithm for selecting a good value for the parameter c in radial basis function interpolation［J］.Adv ComputMath，1999，11:193－210.

［13］Bengrt F，Julia Z.The Runge phenomenon and spatially variable shape parameters in RBF interpolation［J］.ComputMath Appl，2007，54:379－398.

［14］Young D L，FAN C M，HU S P，et al.The Eulerian－Lagrangian method of fundamental solutions for two－dimensional unsteady Burgers equations［J］.Engineering Analysiswith Boundary Element，2008，32:395－412.

(责任编辑:杨 勇)