酉不变范数不等式

刘 新， 杨晓英， 王亚强

(1.四川信息职业技术学院 基础教育部，四川 广元628017;2. 宝鸡文理学院 数学与信息科学学院，陕西 宝鸡721013)

酉不变范数是矩阵理论的一个重要研究领域，在矩阵计算、优化领域、最佳逼近问题以及扰动理论中有着重要的应用。关于矩阵酉不变范数不等式问题是矩阵不等式的研究热点之一，近年来受到国内外学者的广泛关注［1-8］。Bhatia R 等［3］研究了矩阵范数下几何算术平均值不等式;Kittaneh F 等［4］得到一些Young 不等式和Heinz 不等式的改进结果;ZOU Limin 等［5］研究了一些标量不等式，得到在Hilbert-Schmidt 范数下Heinz 不等式的改进式;Bhatia R 等［6］证明了对于所有的酉不变范数，4‖AB‖≤‖(A + B)2‖均成立。

文中在文献［5］的基础上，给出一组新的标量不等式和Hilbert-Schmidt 范数不等式，新不等式推广了文献［5］中的相应结果。

1 预备知识

记Mm，n为m × n 阶复合矩阵，Mn= Mn，n。设λ1(A)，…，λn(A)为矩阵A 的所有特征值，并且| λ1(A)| ≥…≥| λn(A)|。设A，B ∈Mn是半正定矩阵，A ≥B 表示A－B 是半正定的。A ∈Mn的奇异值定义为A*A 的特征值的非负平方根。用s1(A)≥…≥sn(A)表示A ∈Mn的奇异值，幷记s(A)= (s1(A)，…，sn(A))。用‖·‖表示Mn上任意的酉不变范数，即对于所有矩阵A ∈Mn和酉矩阵U，V ∈Mn，都有‖UAV‖ = ‖A‖ 成立。其中，两类酉不变范数尤为重要。一类是Fan-范数‖·‖(k)，即

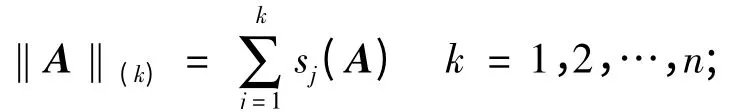
还有一类是Schatten p-范数，即

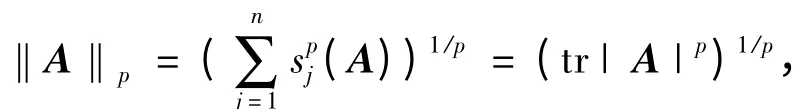
其中，p ≥1;tr 为迹函数;‖·‖(1)= ‖·‖∞为谱范数;‖·‖(n)= ‖·‖1为迹范数。设A = (aij)∈Mn，范数

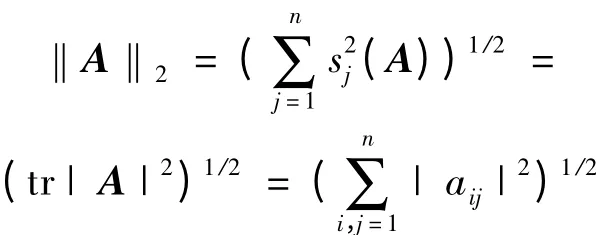
称为Hilbert-Schmidt 范数或Frobenius 范数。显然Hilbert-Schmidt 范数是酉不变范数［1-2］。

文中将利用标量不等式和谱分解定理，得到矩阵酉不变范数的几个不等式。

2 Hilbert-Schmidt 范数不等式

关于酉不变范数不等式的研究［1-8］由来已久。Bhatia Davis 在文献［3］中得到如下结论:设A，B，X ∈Mn，且A，B 半正定，若0 ≤v ≤1，则

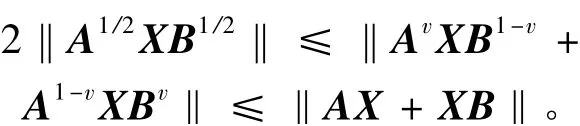
第二个不等式被称为Heinz 不等式。

Kittaneh 在 文 献［4］ 中， 得 到 一 个 在Hilbert-Schmidt 范数下Heinz 不等式的改进式

其中，r0= min{v，1 － v}。

ZOU 等在文献［5］中证明了如下结论:

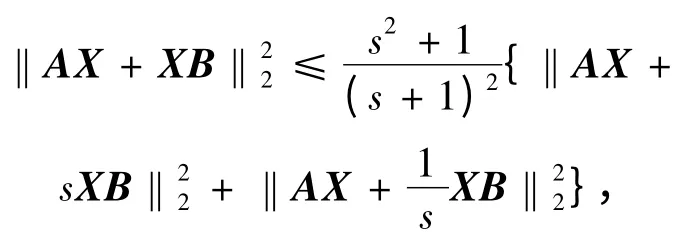
其中，s ∈R，且s ≠0，1。

文中给出关于‖AX + XB‖22 上界的两个新估计式，首先给出几个标量不等式。定理1 设a，b，t ∈R，s ＞0，则

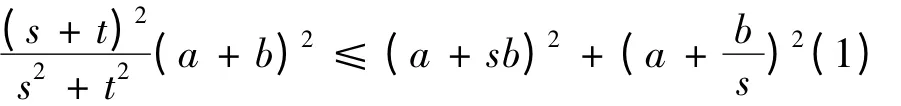
证 令

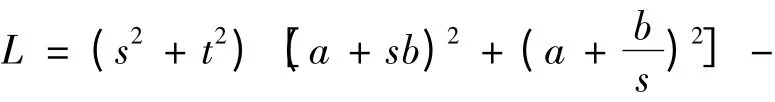
则

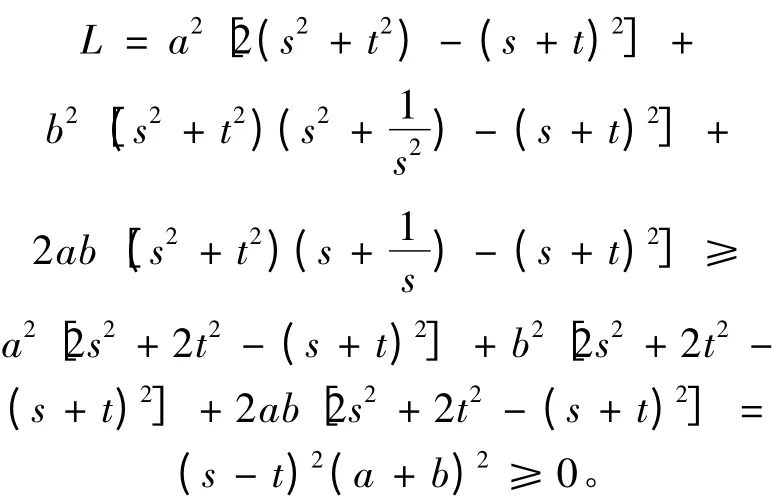
证毕。

注 在t = 1，s ＞0 的条件下，定理1 推广了文献［5］中的引理。

定理2 设a，b，s，t ∈R，且st ＞0，

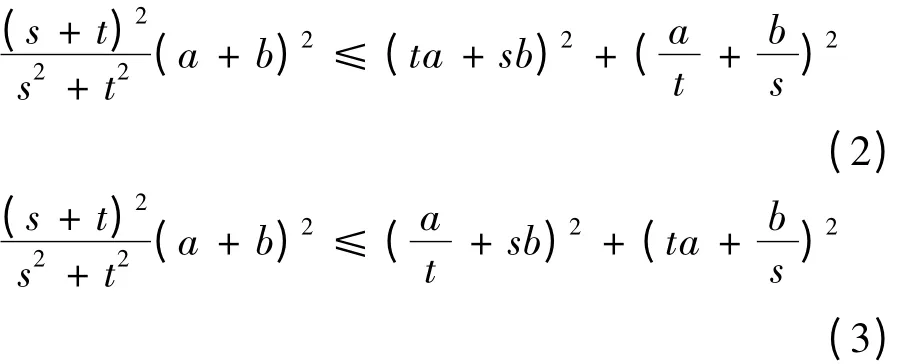
证 令

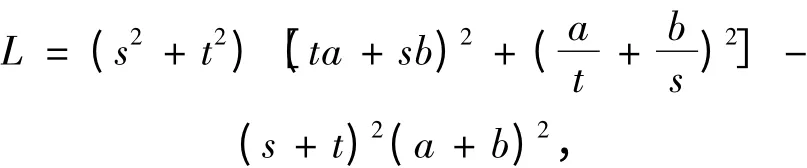
则

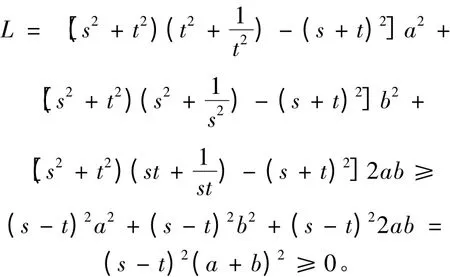
式(2)得证。类似方法，可以证明式(3)同样也成立。证毕。

定理3 设A，B，X ∈Mn，A，B 半正定，若s，t ∈R，且s ＞0，s + t ≠0，则

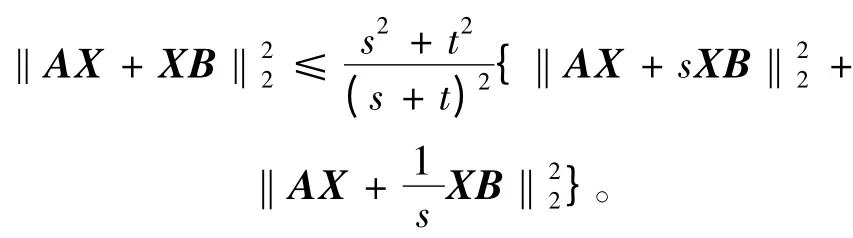
证 因为A，B 是半正定矩阵，所以由谱分解定理［2］可知，存在酉矩阵U，V ∈Mn，使得A =UT1U*，B = VT2V*，其中

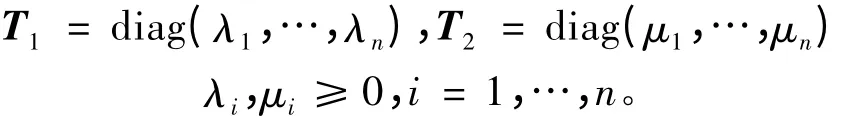
令 Y = U*XV = (yij)n×n，则

因此

同样方法，有

由定理1，可得

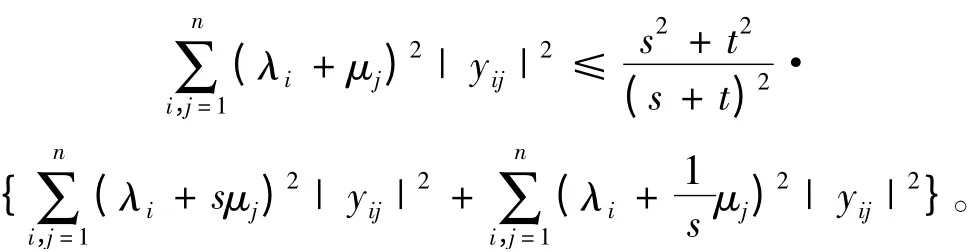
故定理得证。证毕。

注 当s ＞0，t = 1 时，定理3 即为文献［5］中的定理。

利用定理3 的证明方法，结合定理2 可得如下结论。

定理4 设A，B，X ∈Mn，A，B 为半正定矩阵，若s，t ∈R，且st ＞0，则

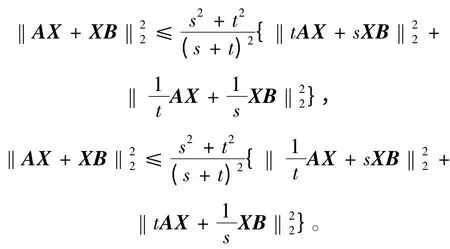
［1］Bhatia R.Matrix Analysis［M］.New York:Springer-Verlag，1997:91-95.

［2］詹兴致.矩阵论［M］.北京:高等教育出版社，2008:54-56.

［3］Bhatia R，Davis C. More matrix forms of the arithmetic-geometric mean inequality［J］. SIAM Journal on Matrix Analysis and Applications，1993，14(1):132-136.

［4］Kittaneh F，Manasrah Y. Improved Young and Heinz inequalities for matrices［J］. Journal of Mathematical Analysis and Applications，2010，361(9):262-269.

［5］ZOU Limin，JIANG Youyi. Inequalities for unitarily invariant norms［J］. Journal of Mathematical Inequalities，2012，6(2):279-287.

［6］Bhatia R，Kittaneh F.Notes on matrix arithmetic-geometric mean inequalities［J］.Linear Algebra and Its Applications，2000，308(1):203-211.

［7］HIAI F，ZHAN Xingzhi.Inequalities involving unitarily invariant norms and operator monotone functions［J］.Linear Algebra and Its Applications，2002，341(2):151-169.

［8］邹黎敏.Heinz 均值凸性的一个注记［J］.浙江大学学报:理学版，2013，40(1):27-28.

ZOU Limin.A note on the convexity of the Heinz means［J］.Journal of Zhejiang University:Science Edition，2013，40(1):27-28.(in Chinese)