基于高斯变异的引力搜索算法

隋永霞， 孙合明

(河海大学 理学院，江苏 南京211100)

万有引力搜索算法(GSA)是2009 年由伊朗克曼大学教授Esmat Rashedi［1］等人提出的一种新的智能优化算法，其起源于物理学中的万有引力现象。牛顿万有引力指出:在宇宙中，任意两个粒子由于万有引力的作用彼此相互吸引，引力的大小与粒子的质量成正比，与它们之间的距离成反比。

目前有关GSA 的研究已经逐渐展开。徐遥等［2］对质量加以权值的基础上对GSA 做了改进，加大了质量大的粒子对算法的影响。刘勇等［3］则将GSA 与混沌算法结合用于解决非线性的极大极小问题。李沛等［4］在标准的GSA 更新粒子位置的基础上引入PSO 思想，将记忆速度引入GSA 中。GSA 同样应用到QoS 的Web 服务选择问题［5］、解决多分类数据集中的分类问题［6］和多目标的经济决策［7］等问题，但是GSA 还存在着易陷入早熟收敛和局部搜索能力不强［8］等问题。

文中通过提出Gaussian 变异因子的思想，较好地解决了GSA 易陷入局部最优问题。最后通过几个测试函数与其它算法进行比较，有效地验证了文中算法的性能。

1 万有引力搜索算法的基本思想

万有引力是自然界中4 种基础力之一，引力的作用无处不在。万有引力搜索算法将所有的粒子都看成有质量的物体，且其能够做无阻尼运动，每个粒子都会受到其它粒子万有引力的影响，产生加速度使其朝向质量大的粒子运动。粒子的质量与其适应值有关，适应值大的其惯性质量也越大，质量小的粒子在朝质量大的粒子逐渐趋近的过程中逼近优化问题的最优解。

设在一个D 维搜索空间中［9］，有N 个粒子，第i个粒子的位置表示为

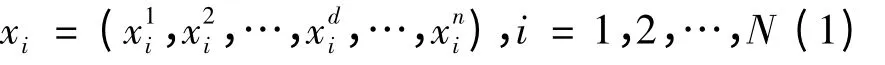
每个粒子的惯性质量由其适应值计算得出，惯性质量越大的粒子越接近问题的最优解。设Mi(t)代表第i 个粒子在t 时刻的惯性质量，则质量Mi(t)的计算公式表示为

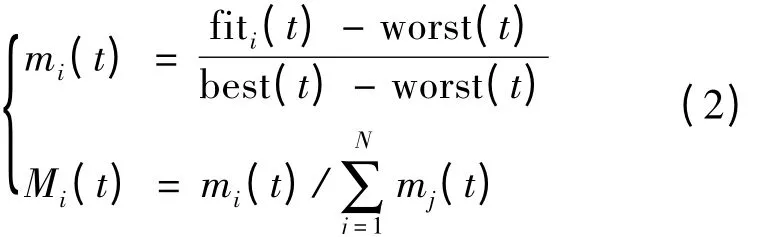
其中，fiti(t)代表粒子i 在t 时刻的适应值，best(t)表示t 时刻的最佳解，worst(t)表示t 时刻的最差解。求极小值问题时，best(t)和worst(t)的定义如下:

求极大值问题时，best(t)和worst(t)的定义如下:

在时刻t，物体j 在第d 维上受到物体i 的引力大小为

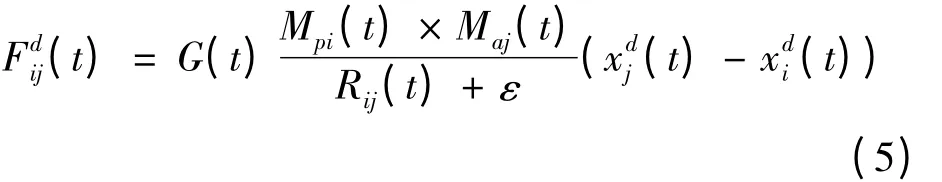
其中，Rij(t)为物体Xi与物体Xj之间的欧式距离，计算公式为

ε 是一个非常小的常量，Mpi(t)表示作用在物体i 上的惯性质量，Maj(t)表示被作用物体j 的惯性质量。G(t)是引力常数，其随宇宙实际年龄的变化而变化，计算公式为

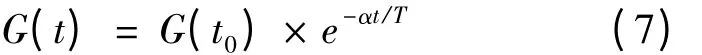
其中G(t)为t 时刻的引力常数值，α 取值为20，T 是最大迭代次数。故在t 时刻，物体i 在第d 维上所受到的合力为

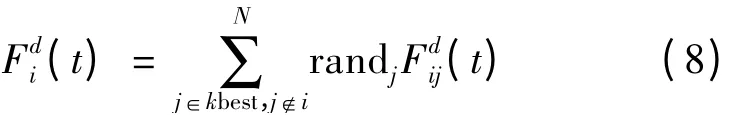
其中randj为0 和1 之间的随机数，kbest 线性地减小，使得算法在搜索空间中有最好的解的物体作用于其它物体。根据牛顿定律可知，在时刻t，物体i 在第d 维上获得的加速度为

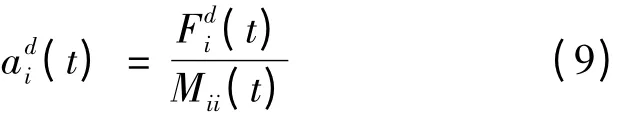
在每一次迭代过程中，物体根据得到的加速度更新物体i 的速度和位置，更新公式为

其中rand 是［0，1］之间的随机数。

2 基于Gaussian 变异的引力搜索算法

2.1 基于Gaussian 变异的GSA 的思想

在万有引力搜索算法中，假设惯性质量最大的粒子所在的位置是所需求解的最优解，则其它粒子所处的位置均可根据其更新公式搜索空间中新的解。基本的万有引力搜索算法同其它智能算法一样存在易陷入局部最优解及早熟收敛等缺点，为了避免算法陷入局部最优解，文中将进化计算过程中的高斯变异［10］融入到引力搜索算法的位置更新中。每个粒子在其搜索区域移动到另一位置时，并不是都像基本的万有引力搜索算法进行速度与位置的更新，而是通过高斯变异加入了一定的不确定性。变异的计算公式为

其中mut(x)为变异后粒子的位置，x 为原先粒子的位置，高斯分布函数

这里取σ 为搜索空间中每一维长度的0.1 倍，均值μ取为0。

基于高斯变异的引力搜索算法以预定的概率来选择变异的个体，并通过高斯分布来确定粒子的新位置。这样在算法初期可以进行大范围的搜索，在算法的中后期通过逐渐减小变异的概率来改进搜索效率，文中将算法变异概率从1 线性减小到0.1。通过动态的改变其变异概率，加快了算法的收敛速度，增加种群的多样性，使得算法容易跳出局部最优。通过仿真实验表明，基于高斯变异的引力搜索算法通过借鉴遗传算法中的变异因子有效地改善了引力搜索算法的全局搜索能力以及加快算法的收敛速度。

2.2 基于Gaussian 变异的GSA 的实现流程

1)随机初始化粒子群中的所有粒子的位置xi和速度vi，并设置迭代次数以及算法中相应的参数;

2)计算每个粒子的相应适应值，利用公式(7)更新引力常数;

3)根据计算得出粒子的适应值利用公式(2)，(3)，(4)计算每个粒子的惯性质量，并且利用公式(5)～(9)计算每个粒子的加速度;

4)产生随机数，若随机数小于变异概率，则根据变异更新粒子的位置，否则利用公式(10)计算粒子的速度，然后更新粒子的位置;

5)若算法未满足终止条件，则返回步骤2);否则，输出该算法的最优解。

3 实验结果与分析

为了验证基于变异的GSA 算法性能，选取6 个经典的测试函数。表1 给出这些测试函数的定义以及相应的取值范围，其中n 代表函数的维数，6 个测试函数的最优解均为0。

对所列的测试函数分别采取标准万有引力搜索算法(GSA)与基于权值的引力搜索算法［2］(GSAGJ)以及基于高斯变异的引力搜索算法(QGSA)进行测试。在所有情况下，粒子的个数为50，维数为30，最大迭代次数为1 000，3 种算法对所列测试函数均进行20 次单独测试，结果如表2 所示。

表1 6 个经典测试函数Tab.1 Six classical test functions

表2 3 种算法对测试函数的平均值与标准差Tab.2 Mean and standard deviation of three algorithms for test functions

从3 种算法对所列测试函数的收敛曲线图1 ～6 可以看出，函数F1和函数F6运用3 种算法所求结果很相近，但是显然QGSA 算法的收敛速度快于GSA 算法以及GSAGJ 算法。从函数F3的收敛曲线图可以看出，QGSA 算法的收敛速度明显快于GSA 算法。从函数F2，F4以及函数F5的收敛曲线图可以看出，GSA 算法以及GSAGJ 算法很快停止进化，这说明算法已经陷入局部最优解中，而对于QGSA 算法，算法的收敛速度明显比GSA 算法及GSAGJ 算法快，并且在GSA 算法及GSAGJ算法陷入局部解之后，QGSA 算法并没有陷入局部解，而是继续进化，优化结果明显好于其它两种算法。

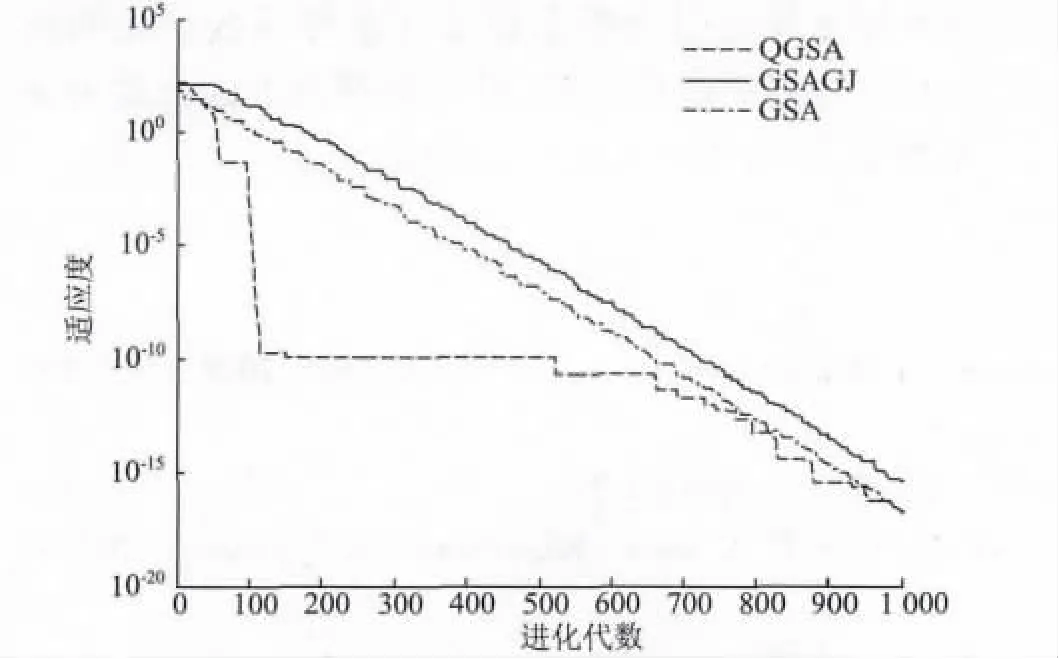
图1 函数F1 中3 种算法优化结果比较Fig.1 Optimization results of three algorithms in function F1

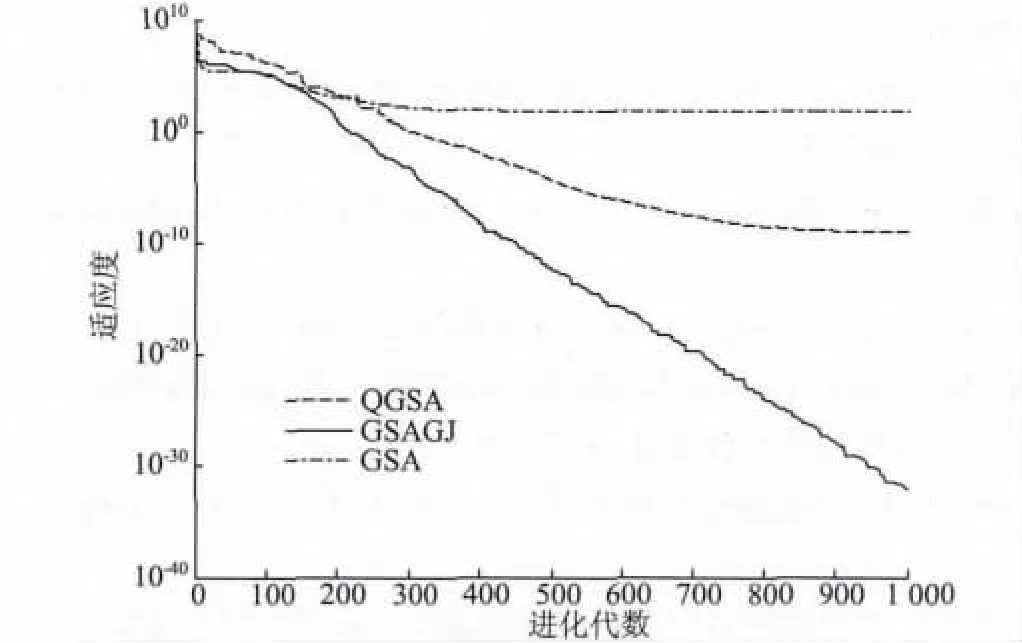
图2 函数F2 中3 种算法优化结果比较Fig.2 Optimization results of three algorithms in function F2

图3 函数F3 中3 种算法优化结果比较Fig.3 Optimization results of three algorithms in function F3

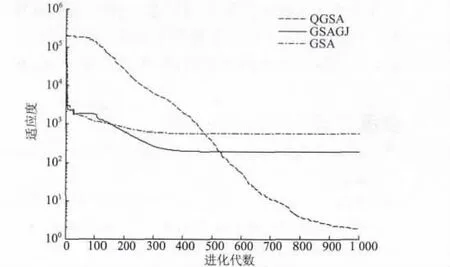
图4 函数F4 中3 种算法优化结果比较Fig.4 Optimization results of three algorithms in function F4

图5 函数F5 中3 种算法优化结果比较Fig.5 Optimization results of three algorithms in function F5

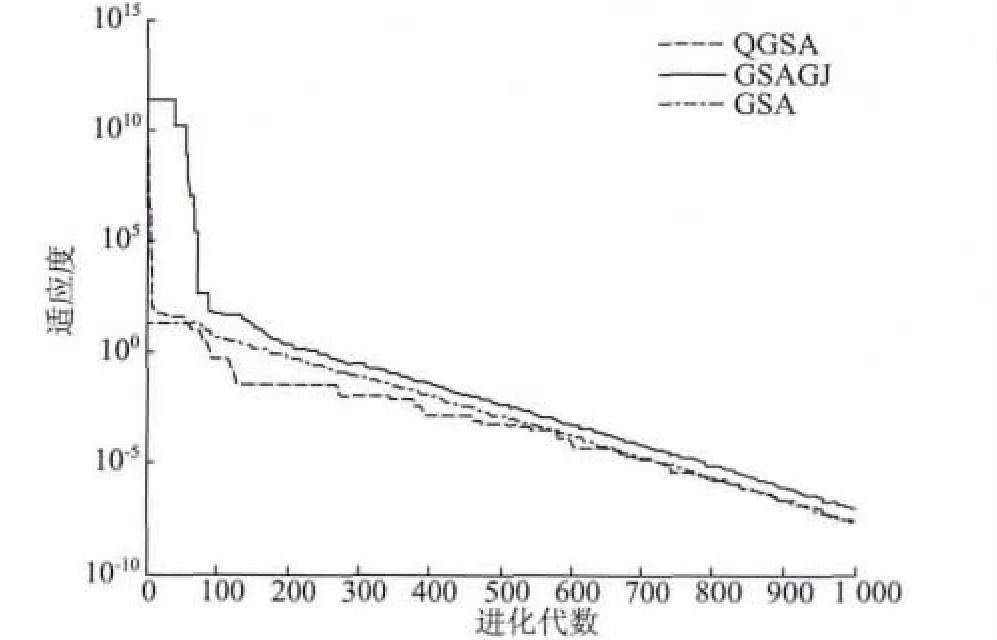
图6 函数F6 中3 种算法算法优化结果比较Fig.6 Optimization results of three algorithms in function F6

4 结 语

在万有引力搜索算法的基础上通过引入遗传算法中的变异因子，提出基于高斯变异的引力搜索算法。通过3 种算法之间的数值实验比较看出，基于高斯变异的引力搜索算法具有较强的优化能力，其收敛速度及其稳定性都要高于基本的引力搜索算法，有效地提高了引力搜索算法的全局搜索能力，并提高了原有算法的求解精度。仿真实验表明，基于高斯变异的引力搜索算法在求解函数优化问题中具有更好的优化性能，但对某些函数优化效果并不明显，尚需要对其进一步探索。

［1］Rashedi E，Nezamabadi-Pour H，Saryazdi S. GSA:a gravitational search algorithm［J］. Information Sciences，2009，179(13):2232-2248.

［2］徐遥，王士同.引力搜索算法的改进［J］.计算机工程与应用，2011，47(35):188-192.

XU Yao，WANG Shitong.The improvement of gravitational search algorithm［J］.Computer Engineering and Application，2011，47(35):188-192.(in Chinese)

［3］刘勇，马良.非线性极大极小问题的混沌万有引力搜索算法求解［J］.计算机应用研究，2012，29(1):47-48，56.LIU Yong，MA Liang.Non-linear minimax problem of chaos gravitational search algorithm［J］.Computer Application Research，2012，29(1):47-48，56.(in Chinese)

［4］李沛，段海滨.基于改进万有引力搜索算法的无人机航路规划［J］.中国科学:技术科学，2012，42(10):1130-1136.

LI Pei，DUAN Haibin. Unmanned aerial vehicle route planning based on improved gravitational search algorithm［J］. China Sciences:Technology Science，2012，42(10):1130-1136.(in Chinese)

［5］Zibanezhad B，Zamanifar K，Sadjady R S，et al.Applying gravitational search algorithm in the QoS-based Web service selection problem［J］.Journal of Zhejiang University Science C，2011，12(9):730-742.

［6］Bahrololoum A，Nezamabadi-Pour H，Bahrololoum H，et al. A prototype classifier based on gravitational search algorithmfJ］.Applied Soft Computing，2012，12(2):819-825.

［7］Mondal S，Bhattacharya A. Multi-objective economic emission load dispatch solution using gravitational search algorithm and considering wind power penetration［J］.International Journal of Electrical Power and Energy Systems，2013，44(1):282-292.

［8］徐耀群，王长举.一种万有引力优化算法及其收敛性分析［J］.哈尔滨商业大学学报，2013，29(1):63-69.

XU Yaoqun，WANG Changju.A gravity optimization algorithm and its convergence analysis［J］.Journal of Harbin University of Commerce，2013，29(1):63-69.(in Chinese)

［9］张维平，任雪飞，李国强，等.改进的万有引力搜索算法在函数优化中的应用［J］.计算机应用，2013，33(5):1317-1320.

ZHANG Weiping，REN Xuefei，LI Guoqiang，et al. Improved gravitational search algorithm application in function optimization［J］.Computer Applications，2013，33(5):1317-1320.

［10］汪定伟，王俊伟，王洪峰，等.智能优化算法［M］.北京:高等教育出版社，2007.