论高考改革下的数学创新试题
夏文涛+马生兰

摘要:随着课程改革的深入和我国高考改革的需要,新颖性、独特性与探究性兼备的数学创新试题很可能会成为今后命题的一种趋势和导向。探析高考数学创新试题的概念、特点和功能,有利于对其整体的理解和把握,对于搞好高中数学教学和高考数学备考复习是十分有益的。
关键词:高考改革 高考数学 数学创新试题
随着课程改革的深入和我国高考改革的需要,新颖性、独特性与探究性兼备的数学创新试题很可能会成为今后命题的一种趋势和导向。对于高考数学创新试题,学界至今还没有明确定义,多数研究者就创新试题的背景、题型、编制、解答展开了一些研究,但是对创新试题的基本问题——概念、特点、功能基本没有明确阐述,这对于进一步研究高考改革下的数学创新试题是不利的。笔者在对相关文献研究的基础上,通过对典型高考数学创新试题的分析与探究,试图初步提出高考数学创新试题的概念、特点、功能。
一、高考数学创新试题的概念
罗增儒教授认为数学题是指数学上要求回答或者解释的事情,需要研究或解决的矛盾[1]。这是目前对数学题广为认可的一种定义,但是其外延尚显广泛。笔者认为,通常情况下,数学题是指在数学教学或数学学习中,基于诊断或测评目的,由数学教师或者教育研究者根据课程标准和命题理论设计、提供给学生解决的数学问题。
数学题的一般形式包含2个基本的部分:条件(已知,前提),结论(未知,要求)。条件一般具有一定的背景(题目背景),需要借助一定的数学语言(文字、符号、图表)提供若干已知信息,结论一般指示求值、求证、判断等。
目前,学界对创新试题还没有统一的认识,基于文献研究和对典型创新试题的探析,笔者认为高考数学创新试题是指根据数学课程标准的理念和要求,依托一定数学命题原理和技术,旨在培养、诊断、测评学生的创新意识与创新能力,在试题背景、试题形式,试题内容或解题方法等方面具有一定的新颖性与独特性的数学题。
二、高考数学创新试题的基本特点
传统的数学题具有接受性、封闭性和确定性等特征[2]。一般来说,数学题考查的内容应该是学生熟知的数学知识,学生通过对例题的程序式的模仿,可以顺畅地完成对数学问题的解答。同时,它的形式结构一般是常规的,条件充分简洁,设问清晰明确,答案唯一确定,学生可以利用所学的数学知识、方法去解决它。另外,它的考查目的在于巩固学生的数学知识,培养学生的数学能力,一般具有一定的挑战性。
除具有以上一般数学题的特点外,数学创新试题还有一些其他比较突出的特点。通过对最近10年来典型数学创新试题的分析和研究,笔者认为高考数学创新试题有以下的特点:
1.立意的鲜明性
立意是指试题的考查目的。高考数学试题的编制遵循“能力立意”的指导思想,这里的能力主要有空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识等7大数学能力。数学创新试题立足学生的知识基础,着力考查数学能力、数学素养,注重测量其发展性学力和创造性学力。因此,数学创新试题的立意重在检测学生对基础知识的掌握情况,考查数学思想方法,考查7大数学能力,特别是考查数学创新意识和创新能力。
2.背景的新颖性
试题的背景是指数学题中学生能够理解的生活现实、数学现实以及其他学科现实。传统意义上,数学试题多是以数学现实为背景。随着素质教育的推进,特别是课程改革的深入发展,以数学现实为背景的数学试题不断丰富,如高等数学背景、竞赛数学背景、数学史背景等;以生活现实、其他学科现实为背景的数学题也逐渐增多,如生活情境问题、物理情境问题等。
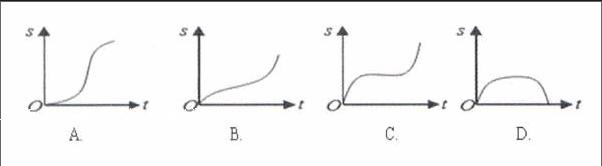
例1.(2008年全国I卷)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
本题以物理学位移与时间的关系为背景,也具有一定的现实生活背景,考查学生运用数学知识与方法解决问题的能力。此题让学生感受到高考数学试题的学科综合性,也体现了数学的广泛应用性,又具有教导我们关注现实生活、学会应用数学的导向意义。
3.形式的灵活性
试题的形式包含数学试题的呈现方式、设问方式以及题型。目前,数学创新试题的呈现形式多样,如采用文字、符号、图形、图表等呈现问题条件,学生需要通过阅读、分析其中的数量关系或者图形关系,推理、判断或者探索其中的规律解决相关问题。开放题引起数学教育界的广泛关注后,很多设问方式灵活多变的试题不断出现,它们要求学生充分运用发散性思维,从多角度、多层次去分析和解决问题。另外,为了诊断、测评的需要,传统的数学题型,如选择题、填空题、解答题等,已经不能满足当前课程改革中教育评价的要求,一些新的题型应时而出,如复合型选择题、复合型填空题等。
例2.(2010年安微卷)若a>0,b>0,a+b=2,则下列不等式对一切满足条件的恒成立的是______(写出所有正确命题的编号)。
①ab≤1;②■+■≤■;③a2+b2≥3;
④a3+b3≥3;⑤■+■≥2。
例2为改良的客观题型,需要多次判断,才能做出正确的选择,我们称之为复合型填空题,它有利于综合考查学生的能力,能够比较理想地预防猜选。
4.内容的综合性
试题的内容是指数学试题所包含的数学知识。课程改革以来,数学高考命题要求从学科的整体高度和思维价值的高度考虑问题,在知识网络的交汇点处设计试题。数学试题包含多个知识点,不仅是数学知识密切关联的内在要求,也是数学测试兼顾范围和题量的必然选择。因此,高考数学多数试题呈现出多个知识点交汇的特点,命题者精心挑选相互交汇的知识板块,合理地控制数目和难度,最终能够生成别出心裁的数学创新试题,全面考查学生知识掌握程度和问题解决能力。
例3.(2011年陕西卷)设集合M={y|y=|cos2x-in2x|,x∈R},N={x||■|<1,x∈R}(i为虚数单位),则MIN为( )endprint
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
本题综合了三角函数、复数、集合等数学知识,设计简洁、突出基础、考查能力,特别是绝对值和复数模的考查,十分巧妙。
5.方法的多样性
解题方法是指解决数学试题所用的一般解答方法和数学思想方法。很多数学创新试题都能一题多解,学生可以根据自己数学学习经验,选择不同的解答方法和思想方法作答。
例4.(2013年重庆卷)在平面上AB1⊥AB2,|OB1|=|OB2|=1,AP=AB1+AB2。若|OP|<■,则|OA|的取值范围是( )
A.(0,■] B.(■,■]
C. (■,■] D.(■,■]
本题是向量的综合应用问题,学生可以根据自己的知识结构,选择不同的解题方法,如解析法、函数法、向量运算法等,至少有10种方法。
三、高考数学创新试题的功能
长期以来,在数学教学和数学学习中,数学解题是最常见的活动形式。它有利于学生对数学概念的理解,对数学基本知识的掌握,对数学思想方法的获得,以及学生能力的发展,对全面提高学生的数学素养有重要的意义,因此,数学解题在数学教育教学中占有重要的地位,数学题对于数学教育教学具有重要的价值和功能。鉴于高考数学创新试题的概念和特点,除包含数学题一般功能外,它还具备鲜明的导向功能、测评功能和诊断功能。
1.导向功能
(1)数学创新试题是检测学生能力和创新意识的现实需要
《普通高中数学课程标准(实验)》(以下简称《高中课标》)[3]明确指出笔试仍是定量评价的重要方式,但要注重考察对数学概念的理解、数学思想方法的掌握、数学思考的深度、探索与创新的水平以及应用数学解决实际问题的能力等。
《2013年高考数学新课标考试大纲》规定创新意识是7大数学能力要求之一,创新意识是理性思维的高层次表现,也是发现问题和解决问题的重要途径,有利于学生对所学的数学知识进行有效的迁移、融合,有利于学生未来的长远发展。
因此,在笔试为主的考评体系下,考查学生的创新能力和创新意识,设置数学创新试题是现实的做法。
(2)数学创新试题是全面发展学生能力和创新意识的必要选择
对于传统的数学题,学生只要学好课本上的那些条条框框的知识,就能照搬课本的知识、方法轻而易举做好它们。在此过程中,学生虽然巩固了所学知识和方法,但是却停留在简单模仿、机械训练的水平,其能力的发展很有限。
数学创新试题一般包含新颖的问题背景,具有灵活的问题形式和设问方式,综合多个知识点、思想方法,设置发散性的解答方法。解答数学创新试题,不仅有利于学生巩固所学知识,引导学生构建知识网络和掌握数学思想方法,发展数学阅读能力、分析和解决问题的能力,也有利于培养学生的数学兴趣和爱好,全面提高学生数学素养。更重要的是,学生通过对数学知识进行有效地迁移、组合和融会,选择数学思想方法创造性解决问题,对学生创新能力和意识的提高有重要意义。
2.测评功能
(1)数学创新试题有利于测评学生的创新能力和创新意识
数学创新试题一般具有新颖的问题背景和一定的深度、广度,兼具多样性、探究性,重点考查学生对数学知识的迁移、组合、融会的能力和分析、解决问题的能力,能够比较理想地测评学生数学创新能力与意识。
(2)数学创新试题有利于更好地选拔优秀人才
由于数学创新试题背景新颖、内容丰富、形式灵活、方法多样,因此它不仅能够考查学生对数学基础知识、基本技能的掌握情况,还能考查其对数学思想方法掌握情况,同时也能够考查其继续学习的潜能,拉开学生分数差距,进而为不同层次的高校提供不同水平的优秀人才。
3.诊断功能
(1)数学创新试题有利于教师提高教学质量
在课堂教学中,为了教学需要,教师必须要准备恰当、典型的数学题,去了解学生理解、掌握的情况,从而调控教学内容、进程。考虑到学生可能会提前预习,以及课本例题比较简单,根据教学需要,教师可以合理地更改例题的背景、形式等,或者选择一些典型的高考数学创新试题作为课堂讲练的例题。这样,教师可以根据学生的做题情况,尽可能全面了解学生的学习情况,准确评估教学效果,调控教学内容、进程,提高课堂教学质量。
(2)数学创新试题有利于学生提升学习水平
根据情况的不同,课后习题的布置各异。课后习题的选择,既要综合考虑学生课堂教学的情况、学生的实际水平,又要兼顾学优生、学差生,同时还要注意发展学生的数学能力和创新意识。由于数学创新试题具有一定的新颖性和探究性,因此,可以选择或改编具有一定梯度、创新度的数学创新试题作为课后作业。教师通过作业情况进一步了解学生学习效果,引导学生加深对数学知识、思想方法的理解和掌握,帮助分析总结学习经验教训,指导学生做好学习、复习计划,这样有利于学生不断提高学习水平。
————————
参考文献
[1] 罗增儒.中学数学解题的理论与实践.南宁:广西教育出版社,2008.
[2] 张奠宙,宋乃庆.数学教育概论.北京:高等教育出版社,2009.
[3] 中华人民共和国教育部.普通高中数学课程标准(实验).北京:人民教育出版社,2003.
[作者:夏文涛(1984-),男,河南信阳人,重庆师范大学数学学院2012级在读硕士;马生兰(1989-),女,青海互助人,重庆师范大学数学学院2013级在读硕士。]
【责任编辑 任洪钺】endprint

