广义子格上模糊蕴涵的延拓方法研究

韩元良，苗文静，隋丽丽

(华北科技学院 基础部 , 北京 东燕郊 101601)

0 引言

设L和K均是非空集合，M⊆L，给定函数f:M→K，如果想把f的定义域从M延拓到L，并且使得延拓后的函数能够保持f的绝大多数性质，应该选择什么样的延拓方法呢？换句话说，对任意x∈LM，如何定义函数值f(x)呢？很多专家和学者对这个问题进行过广泛而深入的研究，并根据不同的研究对象和需要提出了不尽相同的方法(见[3-5], [7])，本文借助广义子格的定义，给出了有界格上模糊蕴涵算子的新的延拓方法，并验证了新方法保持模糊蕴涵算子的大多数基本性质，同时还研究了其他一些重要性质得以保持的条件。

1 预备知识

本文涉及到的一些必要基本概念和结果给出如下，更加详尽的内容可以参考[1-7]。

定义1.1 设L是非空集，如果∧L和∨L是L上的两个二元运算，且对∀x,y,z∈L，满足：

(1)x∧Ly=y∧Lx且x∨Ly=y∨Lx；

(2) (x∧Ly)∧Lz=x∧L(y∧Lz) 且 (x∨Ly)∨Lz=x∨L(y∨Lz)；

(3)x∧L(x∨Ly)=x且x∨L(x∧Ly)=x。

则称为格。

如果格中有元素0L和1L，使得对∀x∈L,x∧L1L=x且x∨L0L=x，则称为有界格，进一步地，格上的偏序关系可以定义如下：

x≤Ly当且仅当x∧Ly=x.

如果格的每个子集都有最大元和最小元，称其为完备格。如果没有特别说明，本文涉及的格均是有界格。

定义1.2 设和是有界格，如果对x,y∈L，映射f:L→M满足：

(1)f(x∧Ly)=f(x)∧Lf(y)；

(2)f(x∨Ly)=f(x)∨Lf(y)；

(3)f(0L)=0M且f(1L)=1M。

则称f是格同态。易知，每个格同态都是保序映射。

定义1.3【1】设是格，M⊆L，若对∀x,y∈M，都有x∧Ly∈M和x∨Ly∈M，则称M是L的子格。

定义 1.4【1】设r是格L到格M的同态映射，如果存在格M到格L的同态映射s，使得r°s=idM，称r是收缩映射，M称为L的收缩核，s称为r的伪逆。

定义 1.5[5]设L和M是有界格，如果M是L的收缩核，则称M是L的(r,s)-子格.。即若M是L的(r,s)-子格，则存在格L到格M的收缩映射r，具有伪逆s。

定义 1.6[5]设L和M是有界格，若收缩映射r:L→M(伪逆是s)满足s°r≤idL(idL≤s°r)，则称r为下(上)收缩映射。此时，M称为L的下(上)收缩核。

定义 1.7[3]设L和M是有界格，M是L的(r1,s)-子格。如果r1是下收缩映射，对同一个伪逆s，存在上收缩映射r2，则称M是L的(r1,r2,s)-子格，记作M◁L。

显然，由定义可知，若M◁L，则s°r1≤idL≤s°r2。

定义 1.8[4]设L是有界格，若二元运算T:L×L→L满足下列条件：

(1)T(x,y)=T(y,x)；

(2)T(x,T(y,z))=T(T(x,y),z) ；

(3) 对∀z∈L，若x≤Ly，则T(x,z)≤LT(y,z)；

(4)T(x,1L)=x。

则称T是一个t-模。

定义 1.9[4]设L是有界格，若二元运算S:L×L→L满足下列条件：

(1)S(x,y)=S(y,x)；

(2)S(x,S(y,z))=S(S(x,y),z) ；

(3) 对∀z∈L，若x≤Ly，则S(x,z)≤LS(y,z)；

(4)S(x,0L)=x。

则称S是一个t-余模。

定义 1.10[2]若映射N:L→L满足下列条件：

(1)N(0L)=1L且N(1L)=0L；

(2)对∀x,y∈L，若x≤Ly，则N(y)≤LN(x)。

则称N为一个模糊非。另外，若模糊非满足N(N(x))=x,∀x∈L，则称N为强模糊非。

定义 1.11[4]设L是有界格，若二元运算I:L×L→L满足下列条件：

(I1)I对第一个变量单调递减；

(I2)I对第二个变量单调递增；

(I3)I(0L,0L)=1L,I(1L,1L)=1L,I(1L,0L)=0L.

则称I为格L上的模糊蕴涵。

对于格L上的模糊蕴涵I，除了必须满足(I1)、(I2)和(I3)之外，有时还会满足其它一些性质。这里列举几个经常讨论的性质如下：

(NP) 对∀y∈L,I(1L,y)=y，称之为左单位性；

(EP) 对∀x,y,z∈L,I(x,I(y,z))=I(y,I(x,z))，称之为可交换性；

(CP) 对∀x,y∈L,I(x,y))=I(N(y),N(x))，称之为反对称性；

(OP) 对∀x,y∈L,I(x,y)=1L⟺x≤Ly，称之为序性质；

(SN) 对∀x∈L,NI(x):=I(x,0L)是强模糊非，称之为强非性；

(CB) 对∀x,y∈L,y≤LI(x,y)，称之为后件边界性；

(IP) 对∀x∈L,I(x,x)=1L，称之为恒等性；

(LI) 对∀x,y,z∈L,I(x,I(y,z))=I(T(x,y),z)，称之为输入律；

(BL) 对∀x,y∈L,I(x,I(y,x))=1L，称之为 Boolean-like law；

(IBL) 对∀x,y∈L,I(x,y)=I(x,I(x,y))，称之为 iterative Boolean-like law.

定义 1.12[3]设M是L的(r1,r2,s)-子格，在M上定义二元运算⊗:M×M→L，若⊗是单调的，且对∀a,b∈M,∀x∈L，满足

r1(a⊗b)=a∧Mb,r2(a⊗b)=a∨Mb

且

r1(x)⊗r2(x)=x.

则称⊗为M上的e-算子。

命题 1.1[3]设M是L的(r1,r2,s)-子格，⊗为M上的e-算子，则对∀a,b∈M及∀x,y∈L，下列性质成立：

(1)a≤Mb当且仅当r1(a⊗b)=a且r2(a⊗b)=b；

(2) 对∀a∈M，有s(a)=a⊗a；

(3)r1(x)≤Mr1(y)且r2(x)≤Mr2(y)当且仅当x≤Ly；

(4)r1(x)=r1(y)且r2(x)=r2(y)当且仅当x=y；

(5) ⊗运算是可交换的。

命题 1.3[3]设M是L的(r1,r2,s)-子格，⊗为M上的e-算子，则

2 广义子格上模糊蕴涵的延拓

本节将首先介绍模糊蕴涵的一种新的延拓方法，其次研究由这种新的延拓方法得到的新的模糊蕴涵是否很好地保持原蕴涵的绝大多数性质，并对其中一些未能保持的性质给出得以保持的条件。

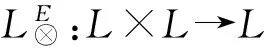
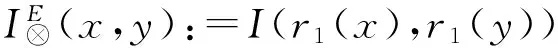
I(r1(x1),r1(y))≥I(r1(x2),r1(y))

且

I(r2(x1),r2(y))≥I(r2(x2),r2(y)).

=I(1M,1M)⊗I(1M,1M)

=1M⊗1M=s(1M)=1L；

=I(0M,0M)⊗I(0M,0M)

=1M⊗1M=s(1M)=1L；

=I(1M,0M)⊗I(1M,0M)

=0M⊗0M=s(0M)=0L.

(NP).

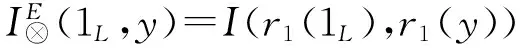
=I(1M,r1(y))⊗I(1M,r2(y))

=r1(y)⊗r2(y)=y.

(CP).

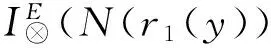
=I(N(r2(y)),N(r2(x)))⊗I(N(r1(y)),N(r1(x)))

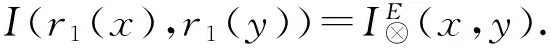
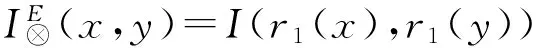
(SN). 假定I满足(SN)，即对∀x∈M,NI(x)=I(x,0)是强非，则

=I(r1(x),r1(0L))⊗I(r2(x),r2(0L))

=I(r1(x),0M)⊗I(r2(x),0M)

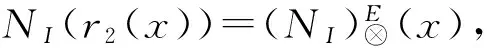
(EP).

=I(r1(x),I(r1(y),r1(z)))⊗I(r2(x),I(r2(y),r2(z)))

=I(r1(y),I(r1(x),r1(z)))⊗I(r2(y),I(r2(x),r2(z)))

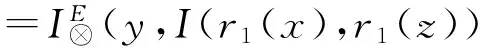
(LI).

=I(r1(x),I(r1(y),r1(z)))⊗I(r2(x),I(r2(y),r2(z)))，

又因为

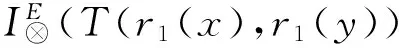
=I(T(r1(x),r1(y)),r1(z))⊗I(T(r2(x),r2(y)),r2(z))

=I(r1(x),I(r1(y),r1(z)))⊗I(r2(x),I(r2(y),r2(z))) .

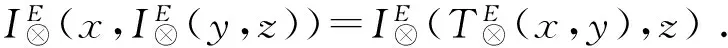
(BL).

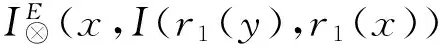
=I(r1(x),I(r1(y),r1(x)))⊗I(r2(x),I(r2(y),r2(x)))

=1M⊗1M=s(1M)=1L.

(IBL).

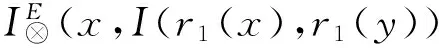
=I(r1(x),I(r1(x),r1(y)))⊗I(r2(x),I(r2(x),r2(y)))

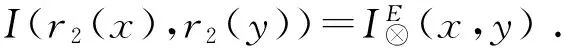
=I(r1(x),r1(0L))⊗I(r2(x),r2(0L))

=I(r1(x),0M)⊗I(r2(x),0M)

=NI(r1(x))⊗NI(r2(x))

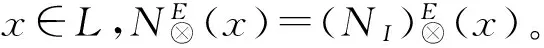
3 结论

本文给出模糊蕴涵的一种新的延拓方法，并验证了其对模糊蕴涵所具有性质的保持性，给出了个别性质得以保持的充分条件，最后还给出了延拓前后两种蕴含生成的模糊非之间的关系。借助这种新的延拓方法，我们还可以研究各种经典蕴涵的延拓形式及其性质。

[1] G. Birkhoff, Lattice Theory[M]. American Mathematical Society, Providence, RI,1973.

[2] M. Baczynski, B. Jayaram. Fuzzy Implications[M], in: Studies in Fuzziness and Soft Computing, Vol.231, Springer, Berlin, Heidelberg, 2008.

[3] E.S. Palmeira, B.C. Bedregal, R. Mesiar, J. Fernandez. A new way to extend t-norms, t-conorms and negations[J], Fuzzy Sets Syst, 2014(240):1-21.

[4] E.S. Palmeira, B.C. Bedregal. Extension of fuzzy logic operators defined on bounded lattices via retractions[J]. Vomput. Math. Appl, 2012(63):1026-1038.

[5] E.S. Palmeira, B.C. Bedregal, J. Fernandez, A. Jurio. On the extension of lattice valued implications via retractions[ J]. Fuzzy Sets Syst, 2014(240)66-85.

[6] E.P. Klement, R. Mesiar, E. Pap. Triangular Norms[M]. Kluwer Academic Publishers, Dordrecht, 2000.

[7] S. Saminger-Platz, E.P. Klement, R. Mesiar. On extension of triangular norms on bounded lattices[J]. Indag. Math, 2008(19):135-150.

[8] B. Jayaram. On the law of importation (x∧y)→z≡(x→(y→z))in fuzzy logic[J]. IEEE Transaction on Fuzzy Systems, 2008(16):130-144.

[9] A. Cruz, B. Bedregal, R.Santiago. On the Boolean-like lawI(x,I(y,x))=1[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2014(22):205-215.

[10] Y. Shi, D. Ruan, E.E. Kerre. On the characterizations of fuzzy implications satisfyingI(x,y)=I(x,I(x,y))[J]. Information Sci, 2007(177)2954-2970.