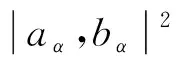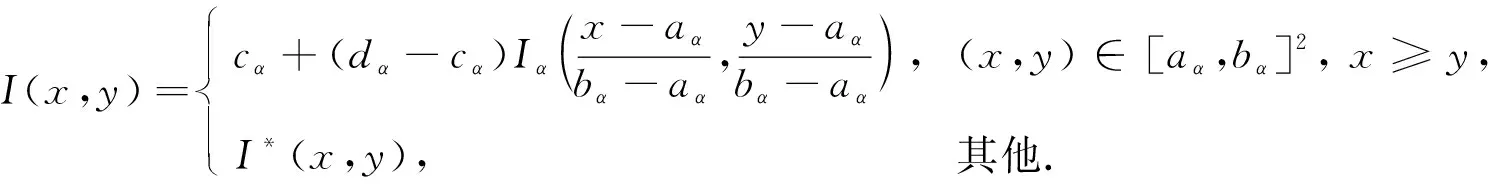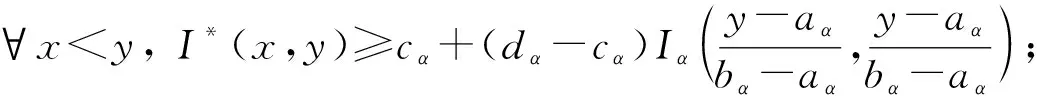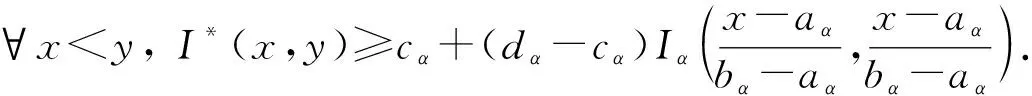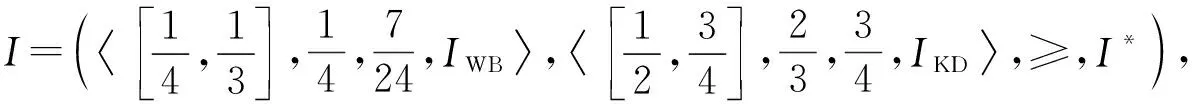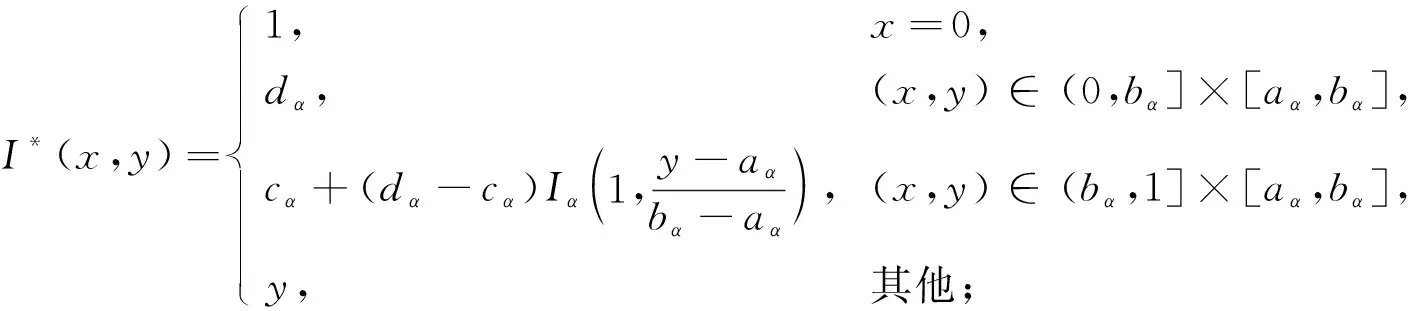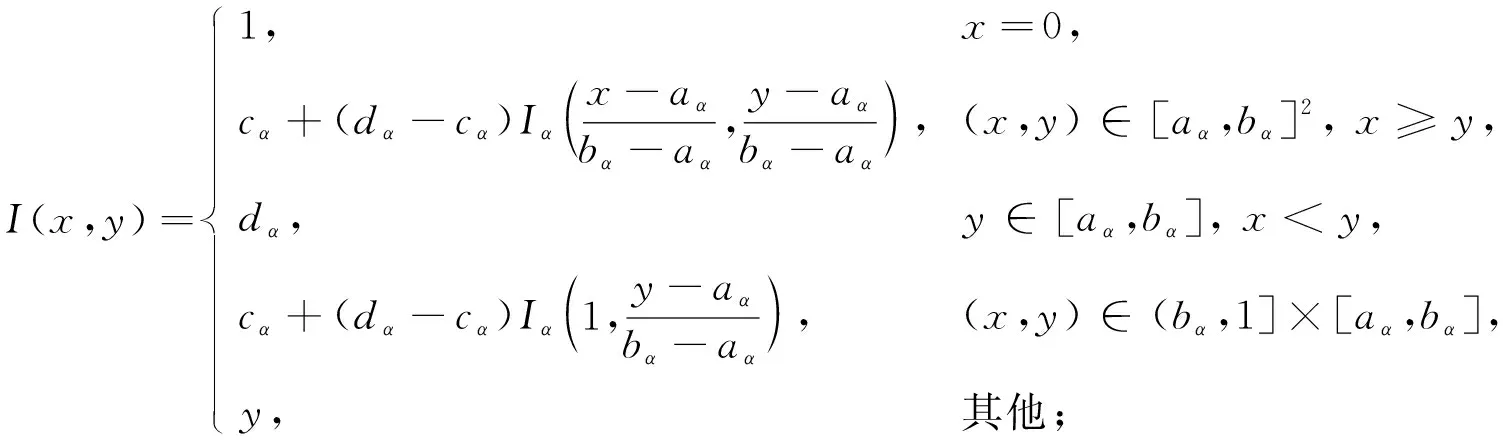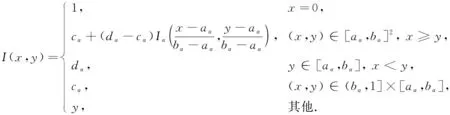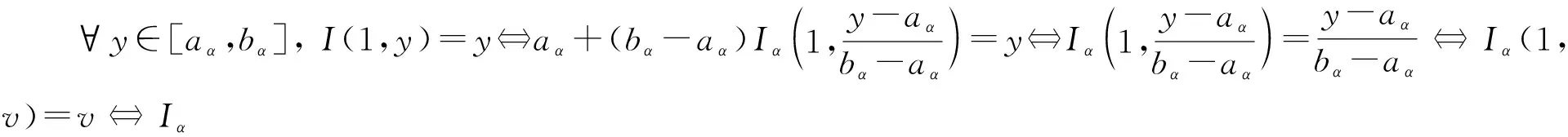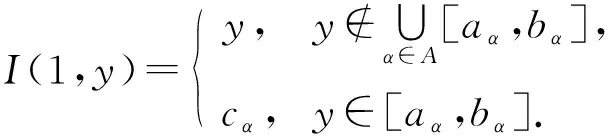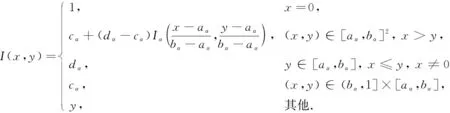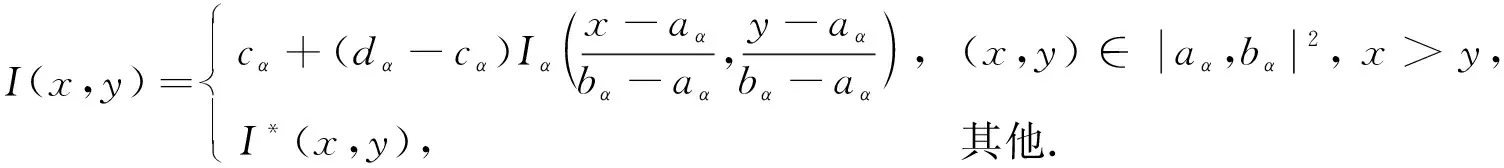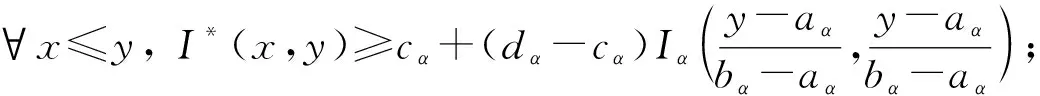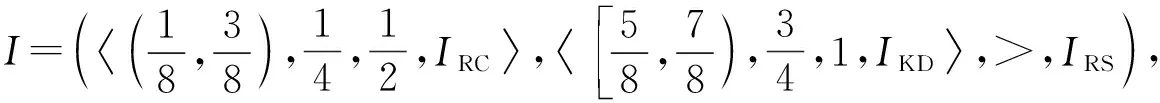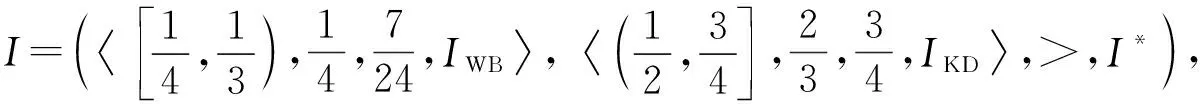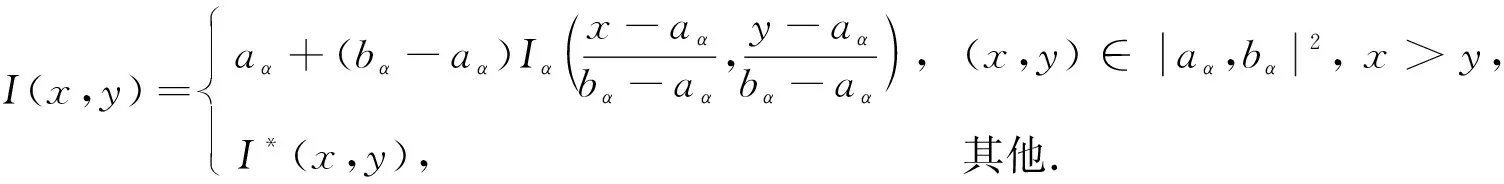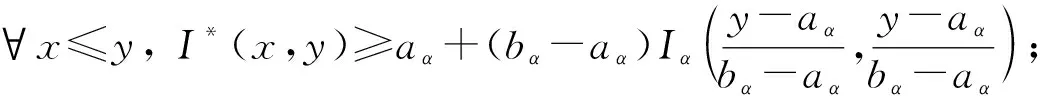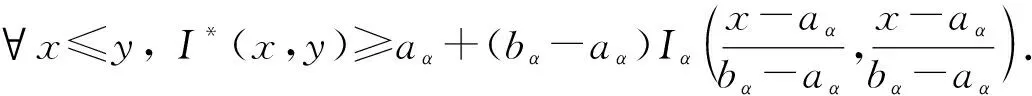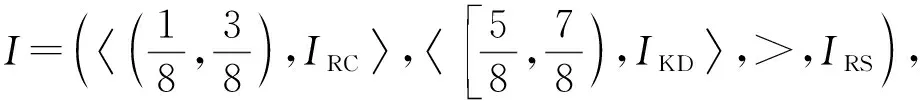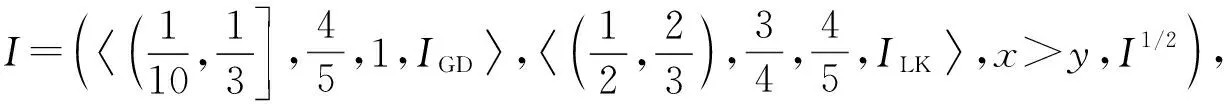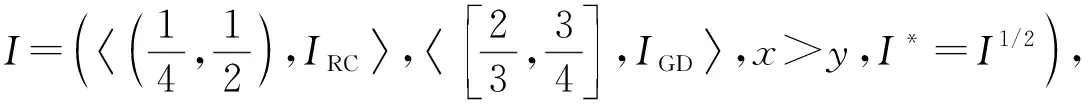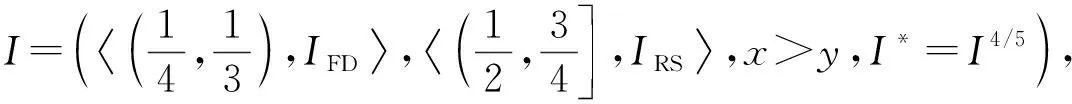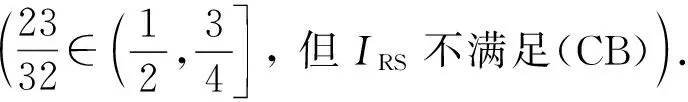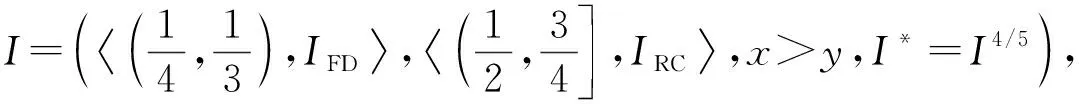模糊蕴涵下三角序和的一般形式
轩素玲, 周红军, 刘 妮
(陕西师范大学 数学与信息科学学院, 西安 710119)
模糊蕴涵是模糊集理论中的一类主要逻辑连接词, 在模糊数学的许多分支中具有重要作用, 如在模糊逻辑中作为蕴涵连接词的语义解释[1-2], 在模糊形态学中用于构造模糊侵蚀算子[3-4], 在图像处理中用于构造图像之间的相似性度量[5], 在模糊粗糙集理论中构造上下近似算子[6-7], 在形式概念分析中导出Galois连接[8-9]等.模糊蕴涵的广泛应用和不确定性知识表示及其逻辑推理对模糊蕴涵模型的大量需求促进了模糊蕴涵的快速发展, 其中新型模糊蕴涵模型的构造及其刻画是其中的研究热点之一.根据不同的构造方法, 模糊蕴涵主要分为五类: (S,N)-蕴涵、R-蕴涵、QL-蕴涵、Yager蕴涵以及序和模糊蕴涵[10-24].本文考虑模糊蕴涵的序和构造.文献[18]给出的序和模糊蕴涵分别借助IGD(Gödel蕴涵)或IRS(Rescher蕴涵)作为单位正方形区域中给定子方形的下三角上的给定一族模糊蕴涵的线性变换的补蕴涵而构造的.本文研究一般模糊蕴涵作为给定一族模糊蕴涵的线性变换的补蕴涵的充要条件, 并将现有的各类下三角上的序和蕴涵纳入到统一框架中, 进而给出模糊蕴涵下三角序和构造的一般形式.
1 预备知识
定义1[25]若对任意的x,y,z∈[0,1],I满足下列条件:
1) 当x≤y时,I(y,z)≤I(x,z);
2) 当y≤z时,I(x,y)≤I(x,z);
3)I(0,0)=1;
4)I(1,1)=1;
5)I(1,0)=0.
则称二元函数I: [0,1]2→[0,1]为模糊蕴涵.
推论1[25]由定义1知, 任一模糊蕴涵I满足下列性质, 分别称为左边界条件和右边界条件:
(LB)I(0,y)=1,y∈[0,1];
(RB)I(x,1)=1,x∈[0,1].
例1[1]如下定义的二元函数I0,I1分别是点式序下最小与最大的模糊蕴涵:
表1列出了其他几种常见的模糊蕴涵.
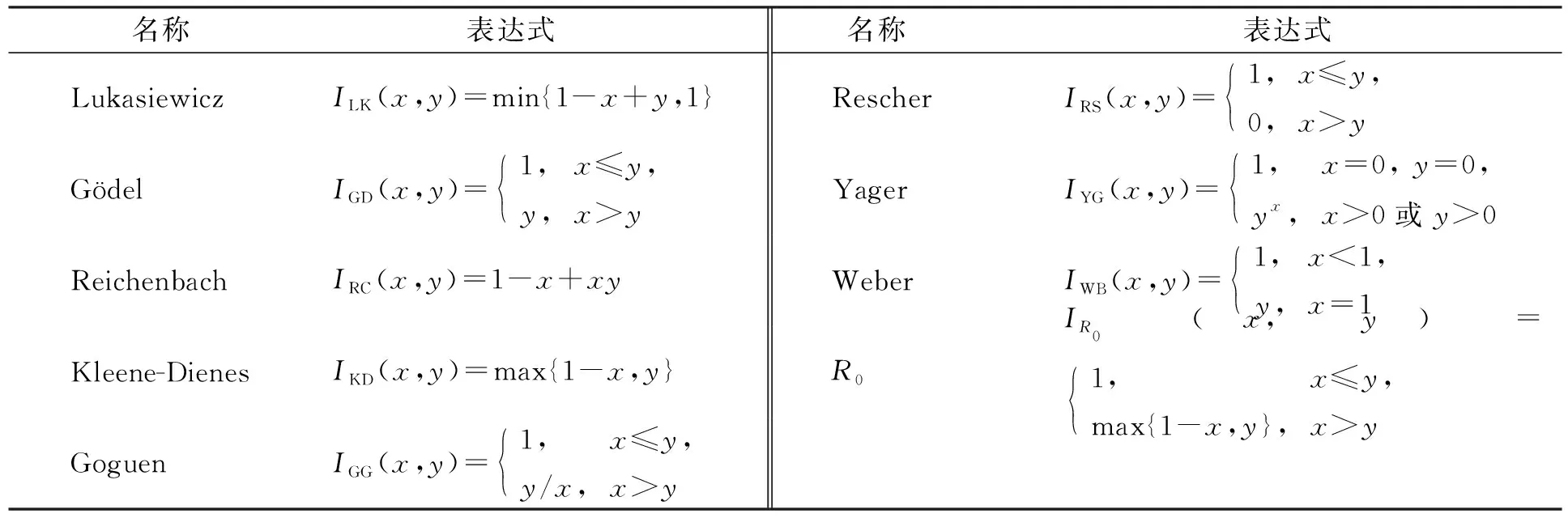
表1 常用的模糊蕴涵
定义2[25-27]设I是模糊蕴涵.
1) 若对任意的y∈[0,1],I(1,y)=y, 则称I满足左单位元性质(简称(NP));
2) 若对任意的x,y∈[0,1],I(x,I(y,z))=I(y,I(x,z)), 则称I满足置换性质(简称(EP));
3) 若对任意的x∈[0,1],I(x,x)=1, 则称I满足恒等性(简称(IP));
4) 若对任意的x,y∈[0,1],I(x,y)=1当且仅当x≤y, 则称I满足序性质(简称(OP));
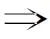

7) 若对任意的x,y∈[0,1],I(x,y)≥y, 则称I满足后件边界条件(简称(CB));



注1设I是模糊蕴涵, 则下列性质等价:
1)I满足(CB);
2)I满足(CB′), 即∀y∈[0,1],I(1,y)≥y.
例2[23]定义二元函数Ic: [0,1]2→[0,1]为
其中c∈[0,1].易验证Ic是模糊蕴涵; 当c=0时,I0=IRS; 当c=1时,I1=IGD.
下面介绍文献[13,18]中给出的几种下三角序和蕴涵, 其中|aα,bα|表示区间(aα,bα),(aα,bα],[aα,bα),[aα,bα]中的任意一个.关于模糊蕴涵的其他序和构造方法可参见文献[23].
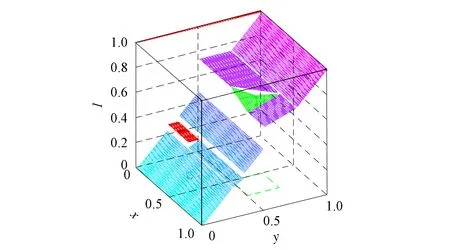
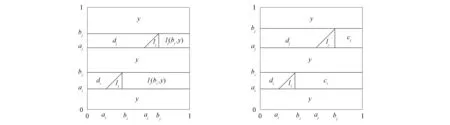
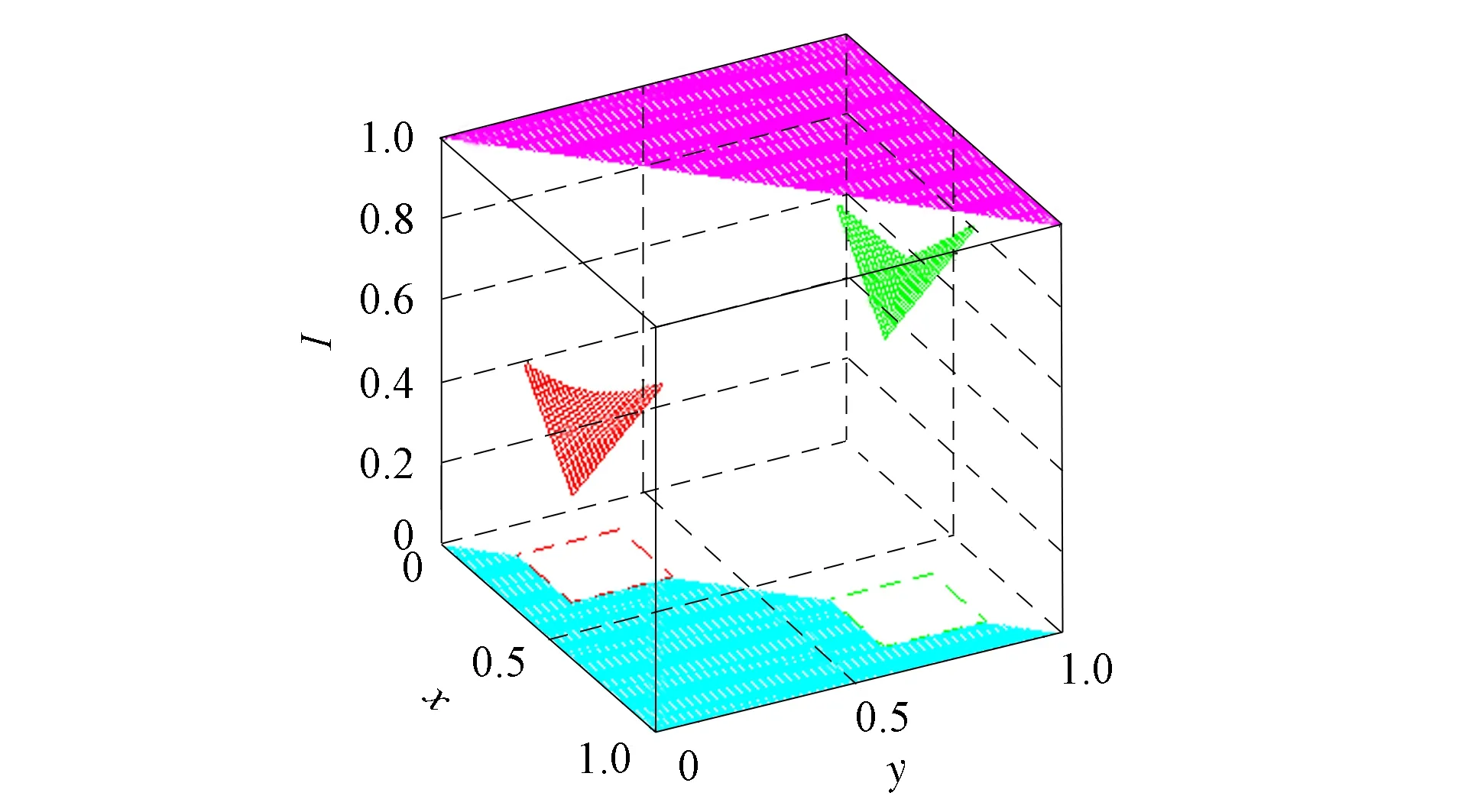
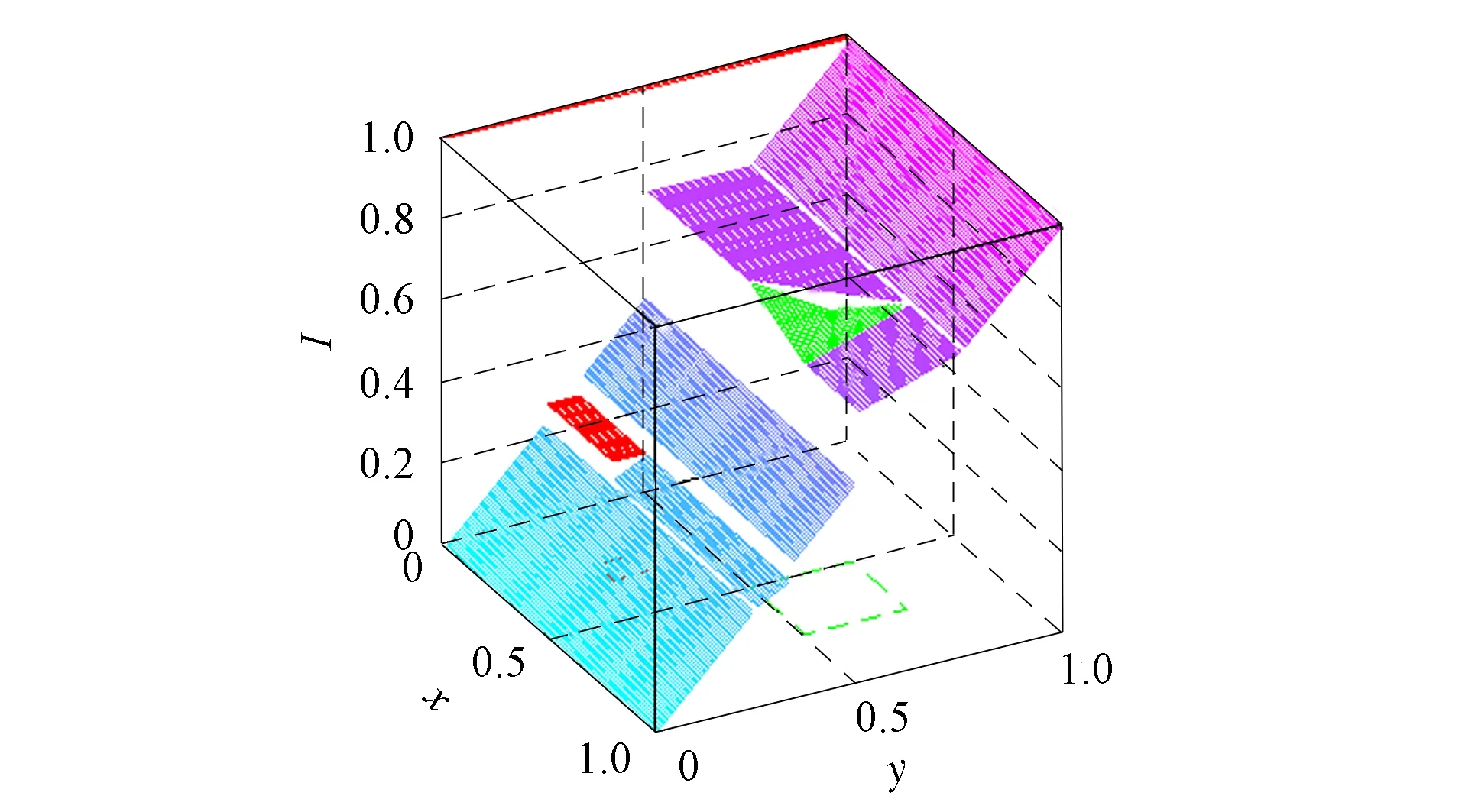
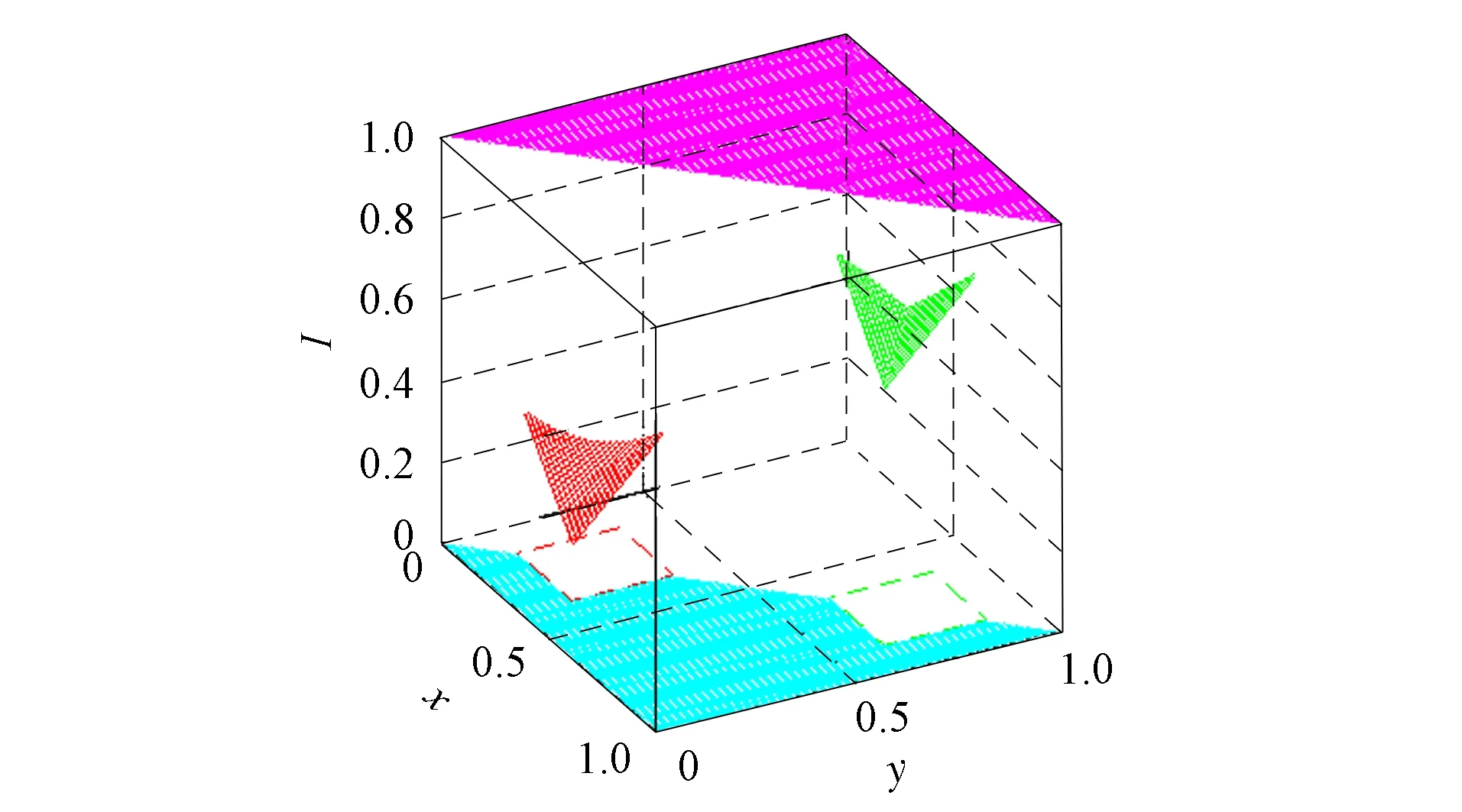
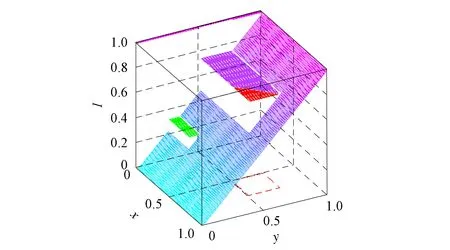
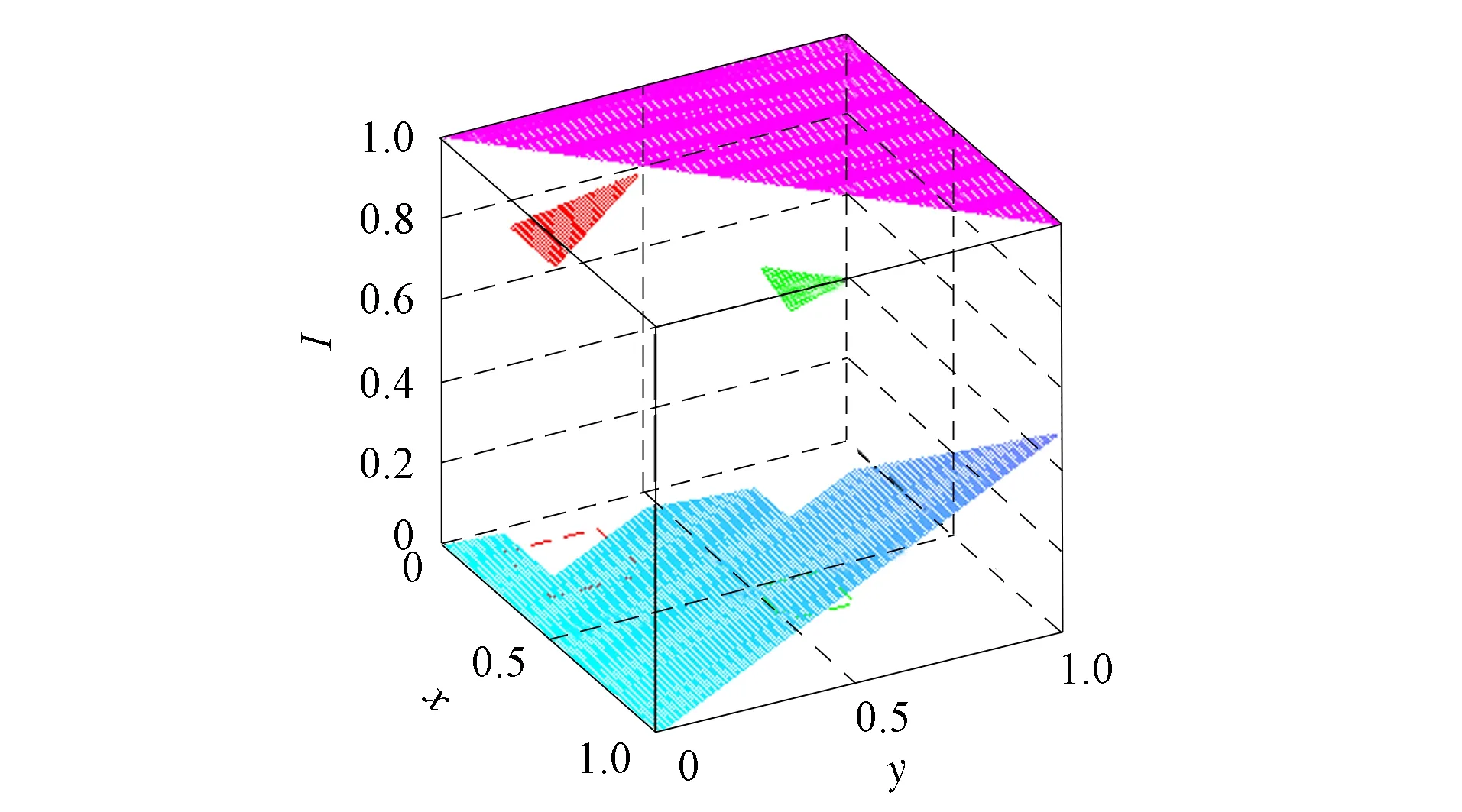
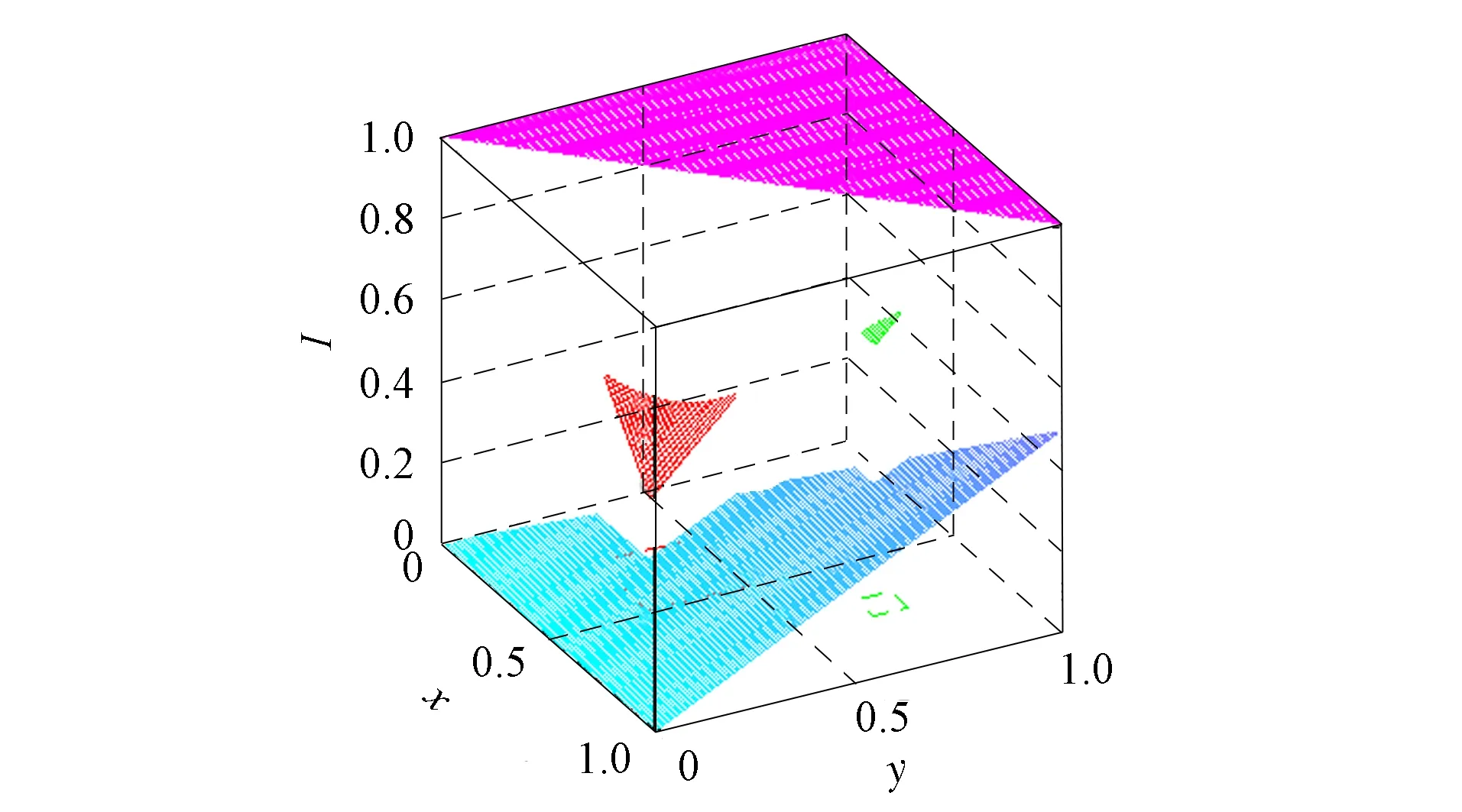
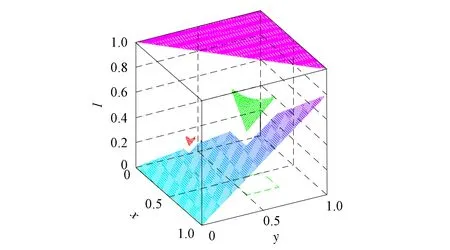
定理1[13]设{Iα}α∈A是一族模糊蕴涵, {[aα,bα]}α∈A是[0,1]的一族互不相交的闭子区间,aα 1) 按下式定义的二元函数I: [0,1]2→[0,1]是模糊蕴涵: (1) 2) 按下式定义的二元函数I: [0,1]2→[0,1]是模糊蕴涵: (2) 定理2[18]设{Iα}α∈A是一族模糊蕴涵, {|aα,bα|}α∈A是[0,1]的一族互不相交的子区间, 且aα 1) 按下式定义的二元函数I: [0,1]2→[0,1]是模糊蕴涵的当且仅当1∉|aα,bα|,α∈A时,Iα满足(CB): (3) 2) 按下式定义的二元函数I: [0,1]2→[0,1]是模糊蕴涵: (4) 定义3设I*是任一模糊蕴涵, {Iα}α∈A是一族模糊蕴涵, {[aα,bα]}α∈A是(0,1)的一族互不相交的闭子区间, {[cα,dα]}α∈A是[0,1]一族闭子区间, 且aα (5) 称I是{Iα}α∈A的序和, 记I=(〈[aα,bα],cα,dα,Iα〉,≥,I*)α∈A. 定理3式(5)定义的二元函数I是模糊蕴涵当且仅当I*满足下列条件: 证明: 必要性.假设I是一个模糊蕴涵,α∈A. 1) ∀y∈[aα,bα]及∀x 因此I*满足条件1). 同理可证I*满足条件2)~4). 充分性.假设I*满足条件1)~4), 则需证明I满足定义1中条件1)~5). ① 设x1,x2,y∈[0,1]且x1 (i) 若∀α∈A,y∉[aα,bα], 由I*的单调性可得,I(x1,y)=I*(x1,y)≥I*(x2,y)=I(x2,y). (ii) 若∃α∈A, 使得y∈[aα,bα], 则需讨论以下4种情形: 若x1 I(x1,y)=I*(x1,y)≥I*(x2,y)=I(x2,y); 若x1 若y≤x1≤bα 若y≤x1 因此I满足定义1中条件1). ② 设x,y1,y2∈[0,1]且y1 (i) 若∀α∈A,x∉[aα,bα], 则由I*的单调性可得,I(x,y1)=I*(x,y1)≤I*(x,y2)=I(x,y2). (ii) 若∃α∈A, 使得x∈[aα,bα], 则需讨论以下4种情形. 若x I(x,y1)=I*(x,y1)≤I*(x,y2)=I(x,y2); 若aα≤y1 若aα≤y1≤x 若y1 因此I满足定义1中条件2). 根据定义3, 显然有I(0,0)=I*(0,0)=1,I(1,1)=I*(1,1)=1,I(1,0)=I*(1,0)=0, 即定义1中条件3)~5)成立. 综上可证I是模糊蕴涵. 则 图1 例3中I的三维图像Fig.1 Three dimensional image of I in example 3 易验证I*满足定理3中的条件1)~4), 故可得I是模糊蕴涵, 其三维图像如图1所示. 命题1设{Iα}α∈A是一族模糊蕴涵, {[aα,bα]}α∈A是(0,1) 的一族互不相交的闭子区间, {[cα,dα]}α∈A是[0,1]一族闭子区间, 且aα 1) 按下式定义的二元函数I*: [0,1]2→[0,1]是模糊蕴涵当且仅当∀α∈A,aα≤cα≤dα≤bα: (6) 2) 按下式定义的二元函数I*: [0,1]2→[0,1]是模糊蕴涵当且仅当∀α∈A,aα≤cα≤dα≤bα: (7) 定理4设I是式(5)定义的二元函数, {[aα,bα]}α∈A是(0,1)的一族互不相交的闭子区间, {[cα,dα]}α∈A是[0,1]一族闭子区间, 且∀α∈A,aα≤cα≤dα≤bα, 其中A是有限或可数指标集.则有: 1) 若I*是式(6)所表示的模糊蕴涵, 则I=(〈[aα,bα],cα,dα,Iα〉,≥,I*)α∈A是模糊蕴涵, 即 (8) 2) 若I*是式(7)所表示的模糊蕴涵, 则I=(〈[aα,bα],cα,dα,Iα〉,≥,I*)α∈A是模糊蕴涵, 即 (9) 式(8)和式(9)的结构如图2所示. 图2 式(8)和式(9)的结构Fig.2 Structures of formulas (8) and (9) 定理5设I是式(8)定义的二元函数.若I是模糊蕴涵, 则: 1)I不满足(IP); 2)I既不满足(LOP)也不满足(OP); 3)I满足(SBC); 4)I不满足(SCC0); 5)I满足(SCC1). 推论2设I是式(8)定义的二元函数.若aα=cα,bα=dα, 则: 1)I不满足(IP); 2)I即不满足(LOP)也不满足(OP); 3)I满足(SBC); 4)I不满足(SCC0); 5)I满足(SCC1); 6)I满足(NP)当且仅当∀α∈A,Iα满足(NP); 7)I满足(CB)当且仅当∀α∈A,Iα满足(CB). 证明: 这里只给出6)的证明, 其他类似. 由式(8)可得∀y∈[0,1], 定理6设I是式(9)定义的二元函数.若I是模糊蕴涵, 则: 1)I不满足(IP); 2)I即不满足(LOP)也不满足(OP); 3)I满足(SBC); 4)I不满足(SCC0); 5)I满足(SCC1); 6)I不满足(NP); 7)I不满足(CB). 证明: 这里只给出6)的证明, 其他类似. 在证明定理3 的充分性时表明, 在子方形[aα,bα]对角线上的取值既可以按照Iα的线性变换取值, 也可以按照I*取值, 不影响其结果.下面按照I*取值, 并把{[aα,bα]}α∈A是(0,1)的一族互不相交的闭子区间修改为{[aα,bα]}α∈A是[0,1]的一族互不相交的闭子区间, 记此序和为 I=(〈[aα,bα],cα,dα,Iα〉,>,I*)α∈A. 推论3设{Iα}α∈A是一族模糊蕴涵, {[aα,bα]}α∈A和{[cα,dα]}α∈A是[0,1]的一族互不相交的闭子区间, 且当aα=0时cα=0, 当bα=1时dα=1,α∈A, 其中A是有限或可数指标集.则有: 1) 若I*是式(6)所表示的模糊蕴涵, 则I=(〈[aα,bα],cα,dα,Iα〉,>,I*)α∈A是模糊蕴涵, 其中 (10) 2) 若I*是式(7)所表示的模糊蕴涵, 则I=(〈[aα,bα],cα,dα,Iα〉,>,I*)α∈A是模糊蕴涵, 其中 (11) 注21) 若推论3中1)的I*满足(LOP)且cα=aα,dα=bα, 则推论3中1)退化为定理1中1). 2) 若推论3)中2)的I*满足(LOP)且cα=aα,dα=bα, 则推论3中2)退化为定理1中2). 下面进一步将式(5)中的闭区间[aα,bα]放宽为|aα,bα|, 给出相应序和是模糊蕴涵的充分条件, 这些结果将推广定理2.由于证明与前面类似, 因此这里仅列举相应结论, 不再证明. 定理7设I*是任一模糊蕴涵, {Iα}α∈A是一族模糊蕴涵, {|aα,bα|}α∈A是[0,1]的一族互不相交的子区间, {[cα,dα]}α∈A是[0,1]一族闭子区间, 且aα (12) 若I*满足下列条件, 则I是模糊蕴涵: 显然IRS满足定理7中条件1)~4), 故可得I是模糊蕴涵, 其三维图像如图3所示. 则 易验证I*满足定理7中条件1)~4), 故可得I是模糊蕴涵, 其三维图像如图4所示. 图3 例4中1)的I三维图像Fig.3 Three dimensional image of I in 1) of example 4 图4 例4中2)的I三维图像Fig.4 Three dimensional image of I in 2) of example 4 推论4设I*是任一模糊蕴涵, (Iα)α∈A是一族模糊蕴涵, {|aα,bα|}α∈A是[0,1]的一个互不相交的子区间族, {[cα,dα]}α∈A是[0,1]一族子区间,aα (13) 若I*满足下列条件, 则I是模糊蕴涵: 显然IRS满足推论4中条件1)~4), 故可得I是模糊蕴涵, 其三维图像如图5所示. 则 易验证I*满足推论4中条件1)~4), 故可得I是模糊蕴涵, 其三维图像如图6所示. 图5 例5中1)的I三维图像Fig.5 Three dimensional image of I in 1) of example 5 图6 例5中2)的I三维图像Fig.6 Three dimensional image of I in 2) of example 5 命题2I是式(12)表示的二元函数, 其中I*=Ic.若∀α∈A及∀y∈|aα,bα|均有cy≤cα, 则I是模糊蕴涵. 证明: 由定理7可知, 只需验证Ic满足定理7中条件1)~4)即可.首先证明Ic满足定理7中条件1), 若(x,y)∈[bα,1]×|aα,bα|,α∈A, 则 因此Ic满足定理7中条件1).同理可证Ic满足定理7中条件2)~4).故可得I是模糊蕴涵. 易验证I满足命题2, 故可得I是模糊蕴涵, 其三维图像如图7所示. 推论5设I是式(13)表示的二元函数,I*=Ic, 则有: 1) 若∀α∈A及∀y∈|aα,bα|有cy≤aα, 则I是模糊蕴涵; 2) ∀α∈A, 若当1∉|aα,bα|时Iα满足(CB), 则I是模糊蕴涵. 易验证I1/2满足推论5中1), 故可得I是模糊蕴涵, 其三维图像如图8所示. 图7 例6中I的三维图像Fig.7 Three dimensional image of I in example 6 图8 例7中1)的I三维图像Fig.8 Three dimensional image of I in 1) of example 7 易验证I4/5满足推论5中2), 故可得I是模糊蕴涵, 其三维图像如图9所示. 图9 例7中3)的I三维图像Fig.9 Three dimensional image of I in 3) of example 7 注31)I是式(12)定义的二元函数, 其中I*=Ic, 则有以下两个结论: ① 若c=0, 则 由命题2可知I是模糊蕴涵. ② 若c=1, 则 由命题2可知, 若∀α∈A,bα≤cα, 则I是模糊蕴涵. 2) 设I是式(13)定义的二元函数,I*=Ic, 则有以下两个结论: ① 若c=0, 则 I是模糊蕴涵, 则推论5中1)即退化为定理2中2). ② 若c=1, 则 ∀α∈A, 若当bα<1时Iα满足(CB), 则I是模糊蕴涵, 反之也成立, 即定理2中1). 综上所述, 本文研究了一般模糊蕴涵作为单位正方形中给定子方形的下三角上给定一族模糊蕴涵线性变换补蕴涵的充要条件, 将已有的各类下三角序和蕴涵归纳到统一框架中, 并给出了模糊蕴涵下三角序和构造的一般形式.本文的序和构造方法从线性变换角度进一步推广了文献[21]中提出的第一种序和构造方法.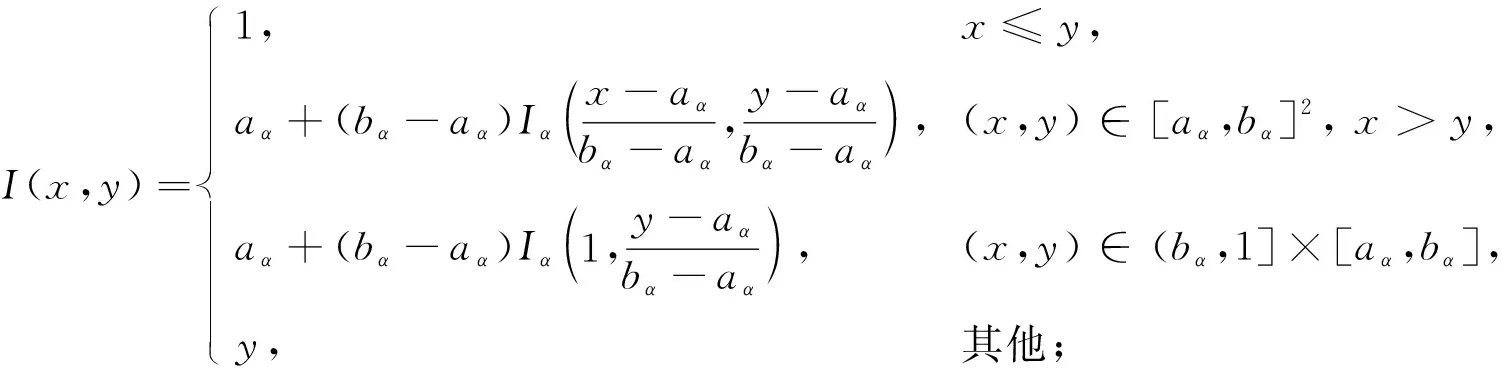
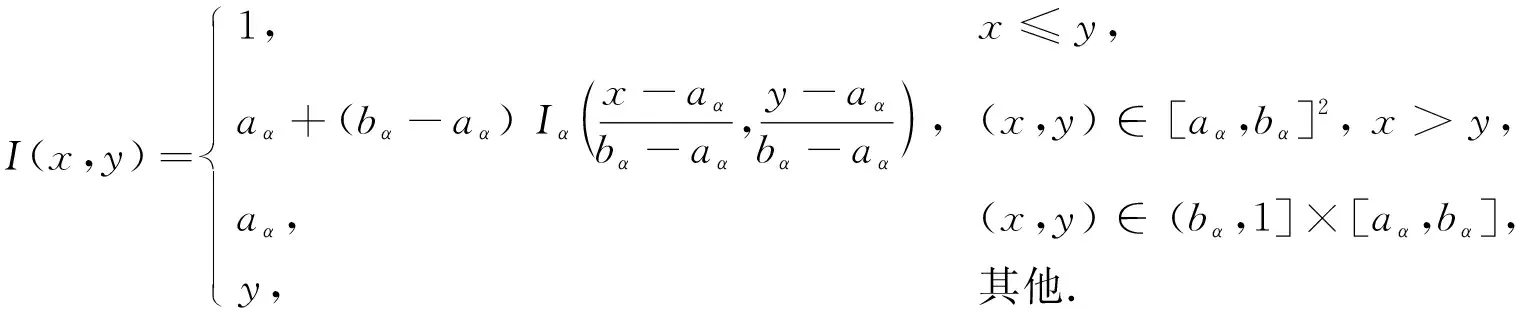
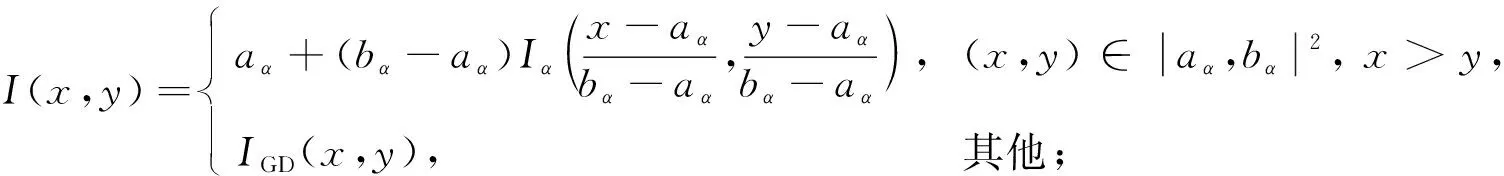
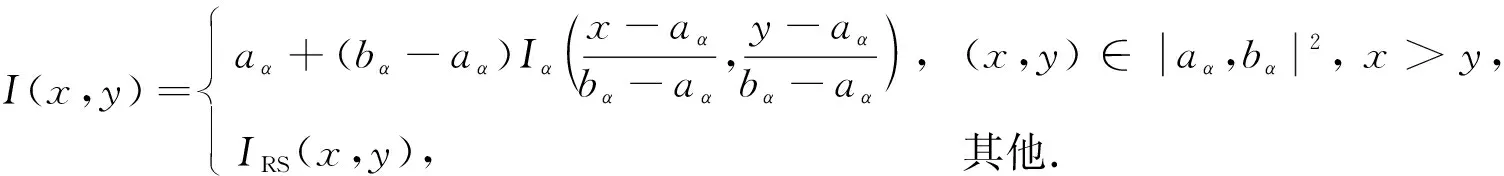
2 主要结果