LQR优化的BP神经网络PID控制器设计

唐伎玲, 赵宏伟, 王婷婷, 胡黄水

(1.长春大学 计算机科学技术学院, 长春 130022； 2.吉林大学 计算机科学与技术学院, 长春 130012；3.长春工业大学 计算机科学与工程学院, 长春 130012)

无刷直流电机(brushless direct current motor, BLDCM) 以其结构简单、效率高、维护费用低、动态响应高等优点, 在航空航天、机器人、电动汽车等领域应用广泛[1-3].转速控制是无刷直流电机驱动领域的一个重要方面[3-4].随着电子技术、传感器技术、自动控制技术和制造技术的快速发展, 研究响应速度快、调节能力强、控制精度高的无刷直流电机调速控制器具有重要意义和应用前景.但复杂的强耦合非线性特性使传统控制方法难以实现良好的速度控制性能.为改善无刷直流电机的暂态和稳态特性, PID(比例-积分-微分)控制器通常是无刷直流电机调速的最佳选择.文献[5-6]提出了基于PI(比例-积分)的无刷直流电机速度控制器, 通过增加比例增益, 提高了速度控制器的灵敏度, 降低了速度超调.但传统PID对增益选择的依赖性较强, 导致无刷直流电机性能下降, 具有各种不确定性和非线性[7].因此, 人们提出了许多方法来简化或改进PID增益整定过程, 其中基于神经网络的算法取得了较好的结果[8-10].

基于神经网络的PID增益更新算法已成功地应用于伺服电机、数控机床等控制中.如文献[11]设计了单神经元PID控制器对无刷直流电机进行控制； 文献[12]设计了一种基于神经网络的永磁同步电机控制策略, 速度环反馈采用BP神经网络实现, 通过系统的状态参数对PI控制器的比例系数KP、积分系数KI进行控制, 该控制策略易实现, 但是该策略在神经网络训练前需通过先验知识确定状态参数.此外, 基于梯度下降的训练算法也是一个耗时的过程, 为此, 人们提出了一些优化方法.文献[13]采用粒子群优化算法初始化自适应PID神经网络控制器的权值, 采用改进的梯度下降算法对PID神经网络的参数进行调整, 但粒子群优化算法初始化PID神经网络的时间较长.经典的最优控制理论已经形成了一种线性二次稳压器, 它可使系统状态轨迹的偏差最小化, 并且只需要最小的控制器努力[14].线性二次调节器(LQR)的这种特性可用于调整PID控制器[15-16].LQR优化PID控制器虽然具有良好的跟踪性能和稳定性能, 但其鲁棒性还有待提高.

为实现无刷直流电机的转速控制, 本文设计一种LQR优化BP神经网络的PID控制器LNPID.该控制器使用LQR算法优化BP神经网络的控制输出, 最佳控制输出调节控制器的KP,KI,KD增益, 以提高控制器的动态适应性和鲁棒性, 使LNPID比传统神经网络PID (NNPID)[12]和LQR优化的PID控制器(LQRPID)[16]控制性能更好.为了验证LNPID的性能, 在不同的工况下进行测试, 并与上述控制器进行超调、欠调、稳定时间、恢复时间和稳态误差等参数的比较.

1 BLDCM的转速控制

三相星形连接BLDCM可转换为如图1所示的电路图.BLDCM的数学模型可用矩阵形式表示为

(1)

其中:Va,Vb,Vc为相电压(V);R为定子绕组电阻(Ω);ia,ib,ic表示电机的相电流(A);L,M分别表示电机绕组的自感和定子绕组间的互感;ea,eb,ec表示各相的反电磁力, 单位为V;P表示转子中极数;θr表示转子位置；J,B,ωr,TL分别表示电机的转动惯量、摩擦系数、角速度和负载转矩.机电转矩为

(2)

图2为BLDCM转速控制系统.由图2可见, 该系统由三相电压型PWM逆变器、三相BLDCM、LQR优化BP神经网络、传统PID控制器、开关逻辑和电机测量传感器组成.在此基础上, 建立了内环和外环两个闭环.外环用于BLDCM的速度控制, 并基于误差e, LQR优化BP神经网络PID控制器为切换逻辑电路提供控制信号, 控制直流总线电压, 从而控制电机的转速.PID控制器由比例项、积分项和微分项组成, 可表示为

(3)

其中e(t),KP,KI,KD,u(t)分别为转速误差、比例增益、积分增益、微分增益和控制输入.通过对连续时间PID方程两边的时间导数进行离散化, 得到离散时间PID控制器, 其表达式为

其中T为采样周期.

图1 无刷直流电机等效电路Fig.1 Equivalent circuit of BLDCM

图2 BLDCM转速控制系统Fig.2 Speed control system of BLDCM

2 BP神经网络最优控制器设计

2.1 BP神经网络设计

图3 BP神经网络结构Fig.3 Structure of BP neural network

采用三层BP神经网络, 其中输入层为3个神经元(神经元个数的选取对应e(k),e(k)-e(k-1),e(k)-2e(k-1)+e(k-2)), 隐含层为6个神经元(神经元个数的选取为多次仿真效果最佳), 输出层为3个神经元(神经元个数的选取对应PID控制器的3个参数), 其结构如图3所示.

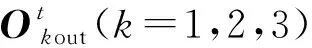
则优化PID增益可表示为

(9)

其中f1(x)和f2(x)是隐藏层和输出层的激活函数, Sigmoid函数为

f1(x)=2/(1+ex)-1,

(10)

f2(x)=1/(1+ex).

(11)

2.2 LQR优化过程

最优伺服系统的设计目标是系统跟踪一定指令信号时误差最小.设BLDCM是一个离散系统, 其离散状态方程为

X(k+1)=FX(k)+GOkout(k),

(12)

Ok(k)=CX(k),

(13)

其中：X(k)是(n×1)维状态向量;Okout(k)是m维控制向量;Ok(k)是l维输出向量,F,G,C分别是(n×n),(n×m),(l×n)维的系统参数矩阵.

Okout(k)=-MX(k)+KE(k),

(14)

(15)

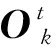
若用带记号“*”的新变量表示系统偏离稳态的平稳状态值(扰动), 则新变量定义为

将式(19)～(21)代入式(12),(13), 得

显然, 从式(22),(23)中分别减去稳态的关系式(16),(18), 可得新的差分方程为

且有

由式(24),(27)可组成一个新的增广系统为

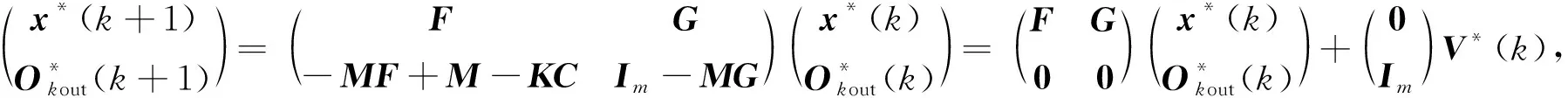
(28)

其中V*(k)为m维向量,

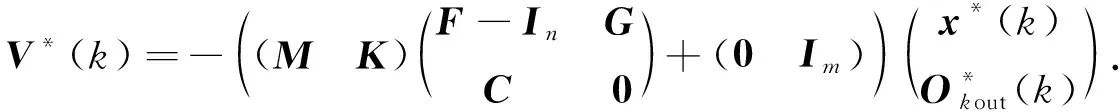
(29)

寻求控制输入V*(k)使如下性能指标J最小:

(30)

其中:Q=CTSC为(n×n)维的半正定矩阵;R为(m×m)维的正定矩阵.在式(28)的约束条件下, 使式(30)表示的性能指标最小.此时, 求V*(k)与线性最优调节器问题相同.于是, 可求得增广系统最优控制器输入为

(31)

2.3 LNPID控制器的设计

BP神经网络具有并行处理能力强、非线性映射能力强、容错性好等优点, 已被用于以不同结构调整PID控制器的增益.但BP神经网络很难达到全局最优解, 收敛时间较短, 参数确定较难, 导致精度低, 收敛性较弱.因此, 将LQR引入到BP神经网络以减少控制误差.

设BP神经网络的输入为xi(k), 输出为Okout(k), 则控制律为

(32)

其中g(xi(k))=g(x1,x2,x3)为BP神经网络的输入与输出非线性映射函数.于是, 最终优化PID增益可表示为

KP,I,D=Ok,k=1,2,3.

(33)

定义训练BP神经网络权值的误差函数为当被控对象动态响应能由式(12)精确表达时, BP神经网络网络的输出为零(Okout(k)=0).将BP神经网络的性能指标定义为

(34)

其中

(35)

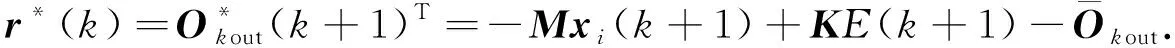
(36)

BP神经网络的连接权值Wij(k)和Wjk(k)采用最速下降法调整：

(37)

其中η为学习率.计算

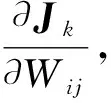
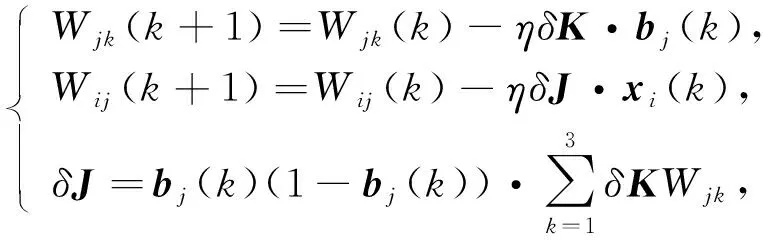
(39)

其中:xi(k)表示BP神经网络的输入;bj为隐层输出;Okout为输出层的输出.

基于LQR优化的BP神经网络的PID控制算法步骤如下：

1) 事先选定BP神经网络的结构, 即选定输入层节点个数m, 根据遗传算法选定隐含层节点个数q及各层间加权系数的初值Wij(0),Wjk(0), 选取学习率η, 并令k=1;

2) 采样得到r(k)和y(k), 计算e(k)=r(k)-y(k);

3) 对e(k),e(k)-e(k-1),e(k)-2e(k-1)+e(k-2)进行归一化处理, 作为BP神经网络的输入;

4) 根据步骤3)计算BP神经网络输出层的输出Okout, 计算此时的控制律Ok, 并由式(33)获得此时控制器的3个调整参数KP,KI,KD;

5) 计算基于LQR优化的BP神经网络控制E(k);

6) 由式(40)计算修正输出层和隐含层的加权系数Wij(k)和Wjk(k);

7) 令k=k+1, 转步骤2), 直到BP神经网络输出层输出误差满足要求为止.

3 仿真分析

为验证LNPID在BLDCM控制系统中的转速控制性能, 借助MATLAB/Simulink工具箱搭建系统模型, 在不同工况条件下对控制器进行仿真分析, BLDCM控制系统仿真模型如图4(A)所示, 其中LNPID控制器如图4(B)所示.采用文献[3]中的BLDCM参数设置: 额定电压为470 V, 额定电流为50 A, 额定转速为2 600 r/min, 定子电阻相R=3 Ω, 定子相电感L=0.001 H, 电压常数为0.146 6 V/(r·min-1), 转矩常数为1.4 N·m/A, 转动惯量J=0.000 8 kg·m2/rad, 阻力因子B=0.001 N·m/(rad·s-1), 极对数P=4.

图4 BLDCM速度控制系统模型Fig.4 Model of speed control system for BLDCM

给定BLDCM的输入转速为2 600 r/min, 负载为空, BP神经网络节点数为3,6,3, 初始权值为[-0.5,0.5]的随机数, 权值随系统动态在线调整, 学习率η=0.05,R=1.根据3种算法仿真实验最终输出数据获得KP,KI和KD参数, 结果列于表1.运行无刷直流电机调速系统模型, 得到的转速响应曲线如图5所示, 各项性能指标列于表2.

表1 KP,KI,KD实验参数

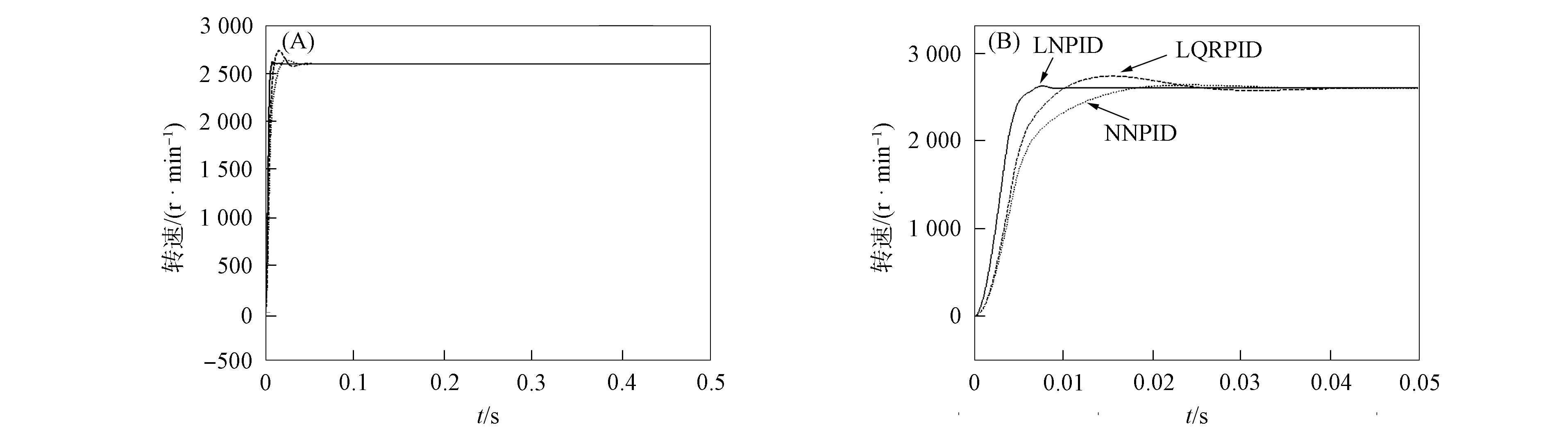
图5 空载状态下转速响应曲线Fig.5 Curves of speed response under no-load state

表2 空载状态下各控制器的性能指标

由图5和表2可见, LQRPID有明显的超调/欠调现象, 超调量最高为137.7 r/min, 欠调量最低为24.3 r/min, NNPID的超调量为38.2 r/min, 欠调量为4.1 r/min; 而LNPID超调/欠调现象较弱, 超调量为25.6 r/min, 欠调量为4.5 r/min.在稳态过程中, LNPID稳定时间最短约0.01 s, 且稳态误差最小, LQRPID稳定时间约为0.052 s, NNPID稳定时间最长约为0.056 s.LNPID在各方面的控制效果均优于其他控制器.

对于实际BLDCM系统, 存在突加的外部干扰, 在控制算法研究中, 系统的鲁棒性也是评判控制策略优劣的一个重要指标.为比较这3种控制算法抗干扰性能的控制效果, 在0.2 s对系统添加3 N的外力干扰, 转速响应曲线如图6所示, 各项性能指标列于表3.由图6和表3可见, 系统在0.2 s突然增加外力干扰时, 3种控制器均产生了波动性响应, NNPID和LQRPID控制器超调/欠调现象明显, LNPID的波动现象最小； LNPID控制器的恢复时间最短为0.05 s, 稳态误差最小为0.4 r/min.因此, LNPID控制器鲁棒性最佳, 具有良好的抗干扰能力.

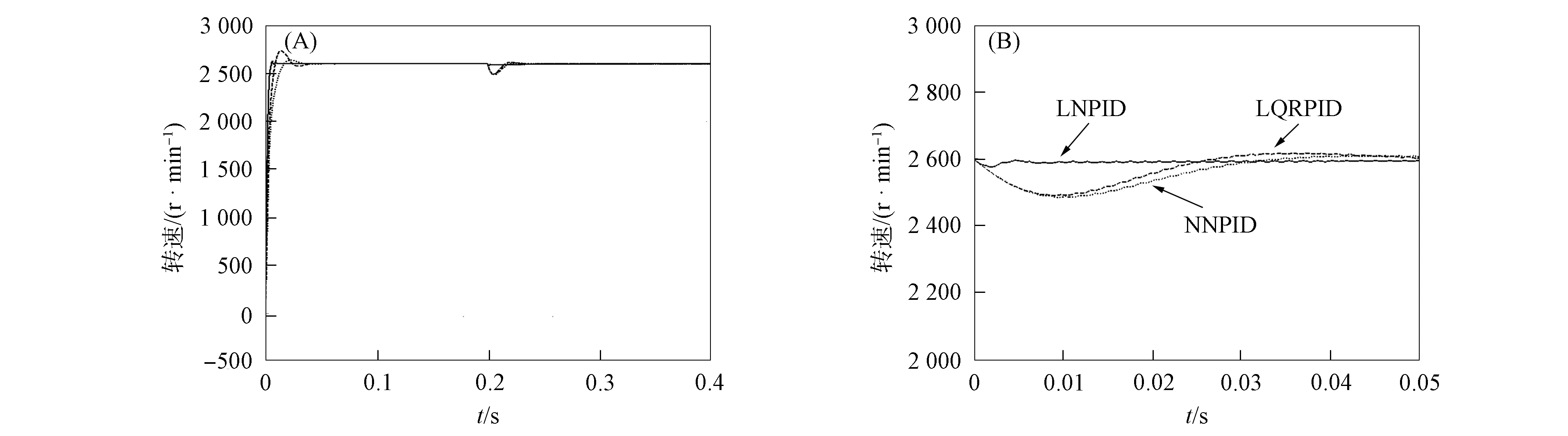
图6 负载状态下转速响应曲线Fig.6 Curves of speed response under load state

表3 负载状态下各控制器的性能指标

Table 3 Performance indexes of each controller under load state

性能指标 NNPID控制器LQRPID控制器LNPID控制器超调量/(r·min-1)34.9217.01-3.5欠调量/(r·min-1)136.01115.8122.34恢复时间/s0.0750.0650.05稳态误差/(r·min-1)1.310.820.4稳态误差/%0.050.0320.015

综上所述, 本文针对无刷直流电机的转速控制问题, 提出了一种基于LQR优化的BP神经网络PID控制器LNPID.采用BP神经网络对PID控制器的增益进行调整, 采用LQR优化BP神经网络的最优输出.在MATLAB/Simulink环境下建立仿真模型, 测试LNPID在空载、负载等工况下的控制性能, 并与NNPID和LQRPID控制器进行了性能指标的对比.仿真结果表明, 在无刷直流电机的各种工况下, LNPID控制器都明显优于其他控制器.