控制活动轮廓演化的快速图像分割方法

金晓民, 张丽萍, 李慧静

(1.内蒙古大学 交通学院, 呼和浩特 010070； 2.内蒙古师范大学 计算机科学技术学院, 呼和浩特 010022)

图像模式识别与场景分析已广泛应用于虚拟现实、模式识别及卫星遥感图像等领域, 图像分割是图像处理中最重要的预处理部分之一[1].目前已有许多图像分割方法, 其中分割效率较高的是阈值分割方法.最大类间方差方法是典型的阈值分割方法[2], 该方法以最小二乘法为基础, 可获取较优的分割结果, 但最大类间方差方法需通过遍历方法寻找类间方差最大阈值, 计算过程较复杂[3].活动轮廓波模型是通过能量最小化检测轮廓的模型, 该模型选取图像目标距离较近的点并设置为初始轮廓, 利用能量函数极小化令轮廓形成弹性形变, 利用轮廓形状迅速获取目标特征, 如何获取图像全部初始轮廓点的最优控制点, 目前还没有好的解决方法[4-5].粒子群优化算法具有灵活、适应性以及寻优能力强等优点, 在图像分割中应用广泛, 但对于复杂、含噪的图像, 单一粒子群优化算法也存在不足.在复杂的图像分割问题中, 单一活动轮廓波模型或者粒子群优化算法均存在“过分割”或“欠分割”现象, 且图像分割速度较慢、鲁棒性较差[6-8].

为求得活动轮廓波模型的图像分割最优控制点, 以获取最佳图像分割结果, 本文将粒子群优化算法与活动轮廓波模型相结合, 提出一种控制活动轮廓演化的快速图像分割方法.先采用粒子群优化算法获取活动轮廓波模型的最优控制点, 再根据最优控制点进行控制活动轮廓演化, 并通过仿真实验分析其性能.

1 算法设计

1.1 活动轮廓波模型

活动轮廓波模型需将封闭曲线设置在所分割图像的目标附近, 利用外部与内部能量使曲线通过最优路径移动, 保持曲线能量不间断更新, 直至曲线到达图像所需分割目标轮廓附近.曲线能量最小时, 分割效果最好.活动轮廓波模型的外部能量与内部能量加权和为曲线能量函数, 内部能量与外部能量分别通过曲线形状及图像获取.活动轮廓波模型离散化公式为

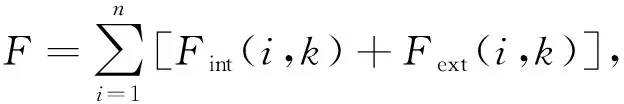
(1)

其中Fint(i,k)和Fext(i,k)分别表示图像迭代点i在第k次迭代时的内部能量和外部能量.

图像的内部能量和外部能量可通过连接能量与弯曲能量及图像梯度表示, 式(1)可分解为

(2)

其中:Fconnect(i,k)和Fcurve(i,k)分别表示迭代点i在第k次迭代时的弯曲能量和连接能量；Fimage(i,k)表示迭代点i在第k次迭代时的图像能量;n表示曲线上离散点数量;β为弹力系数, 其值越大表明曲线收敛速度越高, 弹力系数可有效控制活动曲线的收缩速度;α为强度系数, 活动曲线在α过大时较难形成弯曲, 活动曲线在α过小时极易产生形变.式(2)中的αFcurve(i,k)+βFconnect(i,k)与式(1)中Fint(i,k)相同； 式(2)中γFimage(i,k)与式(1)中Fext(i,k)相同.Fconnect(i,k)描述活动曲线长度的变化率, 属于离散点间的一阶微分, 曲线收敛过程中的连续性可通过Fconnect(i,k)控制.Fcurve(i,k) 描述曲线的曲率变化,Fcurve(i,k)为离散点间二阶微分的平方和, 控制活动曲线移动至图像目标, 活动曲线移动至图像目标速度由系数α控制.通过Fimage(i,k)判断初始化曲线是否收敛至图像分割的真实边界.图像能量最大处与最小处分别为边界处曲线图像及非边缘处图像,γ表示图像力系数,Fimage(i,k)通常为负, 且γ>α,β.

1.2 粒子群优化算法

粒子群优化算法是利用鸟群飞行觅食行为中个体间互相协作获取群体最优的群智能算法, 其通过迭代方式获取问题最优解.用粒子群优化算法求解问题时, 先将所需解决问题设置为粒子, 设空间为b维, 令b维空间中数量为n的粒子运动形成粒子群.寻找问题最优解时, 令空间中随机形成粒子群, 利用粒子群迭代寻优获取问题最优解, 粒子在迭代过程中利用局部最优解与全局最优解调整迭代速度与粒子位置, 更新新的粒子群, 并计算适应度函数, 根据所获取的适应度值将无法继续寻优的粒子淘汰, 粒子群不断更新直至收敛获取全局最优解, 粒子群更新速度公式为

vk+1=wvk+c1r1(qbestk-xk)+c2r2(qgbestk-xk),

(3)

粒子群位置更新公式为

xk+1=xk+vk+1,

(4)

其中：xk和vk分别表示粒子的目前位置和速度矢量；qbest和qgbestk分别表示粒子在迭代过程中的最优解及迭代过程中粒子群的整体最优解；w表示加权因子, 其调整公式为

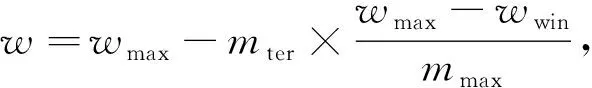
(5)

式中,wmax为惯性权重最大值,wmin为惯性权重最小值,mmax和mter分别为最大迭代和当前迭次数.

粒子群优化算法中粒子通过不断更新迭代使空间中粒子具有最优全局搜索能力及精细的局部搜索能力, 并通过动态调整限制粒子群中各粒子不同维度速度, 使粒子搜索速度小于vmax, 限制粒子搜索速度使粒子群中的粒子在迭代过程中避免发生失序情形, 并使粒子群全局寻优能力随着粒子数量增加而增加.

1.3 改进算法

将粒子群优化算法的适应度函数与活动轮廓波模型相结合, 提出一种控制活动轮廓演化的快速图像分割方法.利用一组控制点描述曲线T, 通过控制点迭代实现能量最小化.将活动轮廓波模型积分形式离散化至差分形式, 获取控制点qi(x,y)附近的能量, 即

Fi,j=Fint+Fext+Farea.

(6)

曲线轮廓的弹性与连续性通过内部能量控制, 公式为

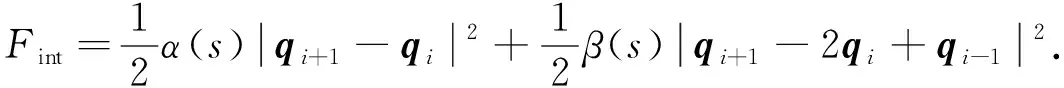
(7)

曲线向图像目标边缘移动由外部能量控制, 公式为

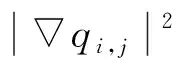
(8)

通过增设一个面积, 使曲线向图像分割目标区域移动, 公式为

Farea=δTarea,

(9)

其中δ表示面积力.Tarea在搜索到图像分割目标区域位置时, 能量逐渐接近最小化.用活动轮廓波模型获取粒子群优化算法的最终适应度函数公式为

ffit=ω1Fint+ω2Fext+ω3Farea,

(10)

其中ωi(i=1,2,3)表示权值.

粒子群优化算法利用活动轮廓波模型能量获取存在面积因素的适应度函数, 通过适应度函数约束粒子群优化算法中的寻优粒子, 粒子位置与速度经过不断更新与迭代获取全局最优值, 即最优控制点.对图像中的全部初始轮廓点采用粒子群优化算法, 获取最优极值轮廓点, 实现目标图像的准确分割.

控制活动轮廓演化的快速图像分割方法步骤如下：

1) 初始化粒子群优化算法中的最大迭代次数、加速因子、惯性因子、群体数目等参数, 为避免粒子搜索溢出, 设置粒子搜索范围边界；

2) 初始化粒子群优化算法中粒子初始位置及初始速度；

3) 根据式(10)利用活动轮廓波模型获取粒子群优化算法的最终适应度函数值；

4) 记录粒子群优化算法过程中粒子的局部最优位置及最佳适应度值, 更新粒子的全局最优位置；

5) 更新粒子位置、粒子速度及粒子的适应度函数值；

6) 当粒子符合迭代次数最大值时, 转步骤7); 否则, 转步骤5)；

7) 当图像全部初始轮廓点计算完成时, 通过迭代更新获取图像全部轮廓点最优值, 实现图像分割.

2 仿真实验

2.1 实验环境

为验证粒子控制活动轮廓演化快速图像分割方法的有效性, 采用如下仿真实验平台进行验证测试实验: CPU为Inter酷睿i7-970, 内存为32 GB, 硬盘为500 GB, 操作系统为Windows XP, 编程工具采用MATLAB 2018.粒子群优化算法的相关参数： 最大迭代数为100, 群体数为15,c1=c2=2.选取网络图像研究库中的10幅图像作为实验对象, 从10幅图像中随机挑选4幅如图1所示的原始图像.为分析本文方法图像分割的优越性, 选择文献[9]和文献[10]的图像分割方法进行对比实验.

图1 原始图像Fig.1 Original images

2.2 图像分割的主观视觉效果分析

将图1中的4幅原始图像分别采用不同方法分割, 分割图像结果如图2～图4所示.由图2～图4可见, 采用本文方法可有效将原始图像分为不同区域, 且图像分割边缘平滑, 验证了本文方法图像分割的有效性, 而对比方法出现了许多错误的分割点, 导致丢失一些重要信息, 得到了“过分割”或“欠分割”的结果.

图2 文献[9]方法的图像分割结果Fig.2 Image segmentation results of document [9] method

图3 文献[10]方法的图像分割结果Fig.3 Image segmentation results of document [10] method

2.3 图像分割的客观效果分析

2.3.1 图像分割精度对比 采用10幅原始图像和加入噪声的图像作为测试对象, 统计其图像分割精度, 结果列于表1.由表1可见, 3种方法对原始图像分割精度均明显高于加入噪声后图像, 本文方法的原始图像和含噪声图像的分割精度均高于96%和93%, 神经网络方法和深度学习方法原始图像和含噪声图像的分割精度均低于93%和91%.对比结果表明, 本文方法不仅具有较高的分割准确性, 且具有极高的抗噪性能, 可应用于复杂的图像分割中.

图4 本文方法的图像分割结果Fig.4 Image segmentation results of proposed method

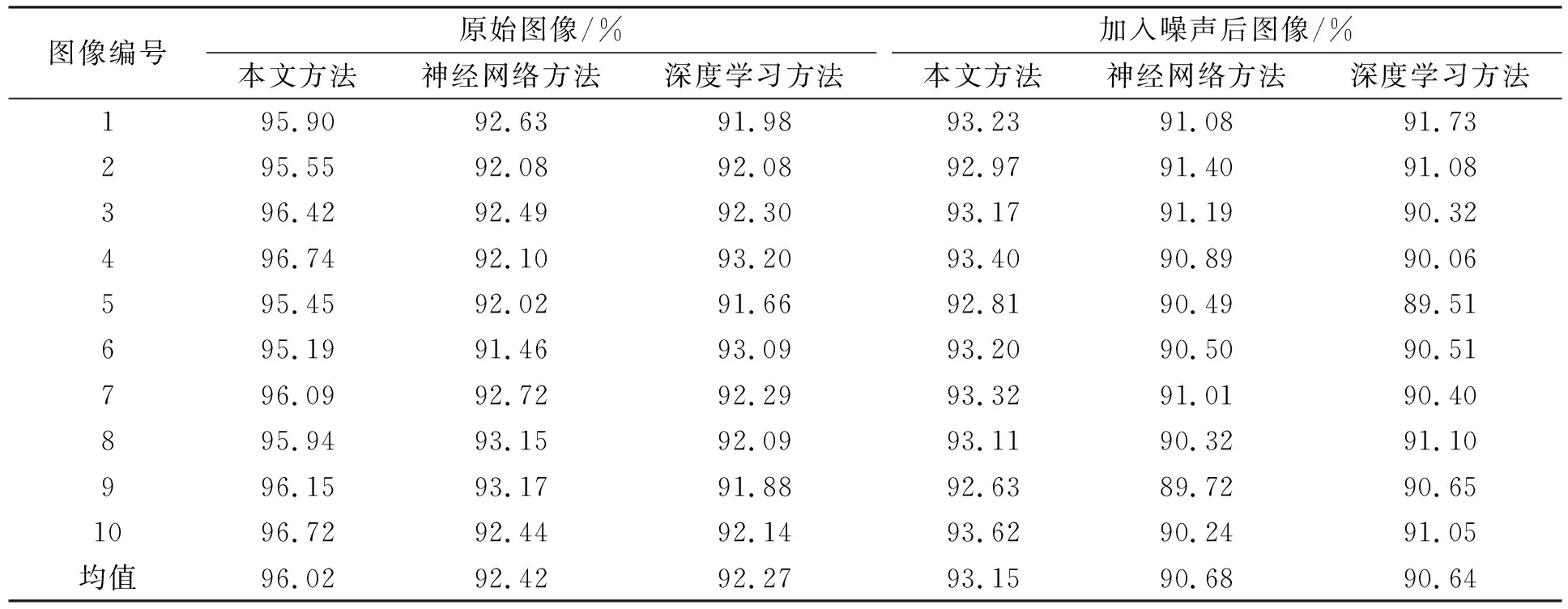
表1 不同方法的图像分割精度对比

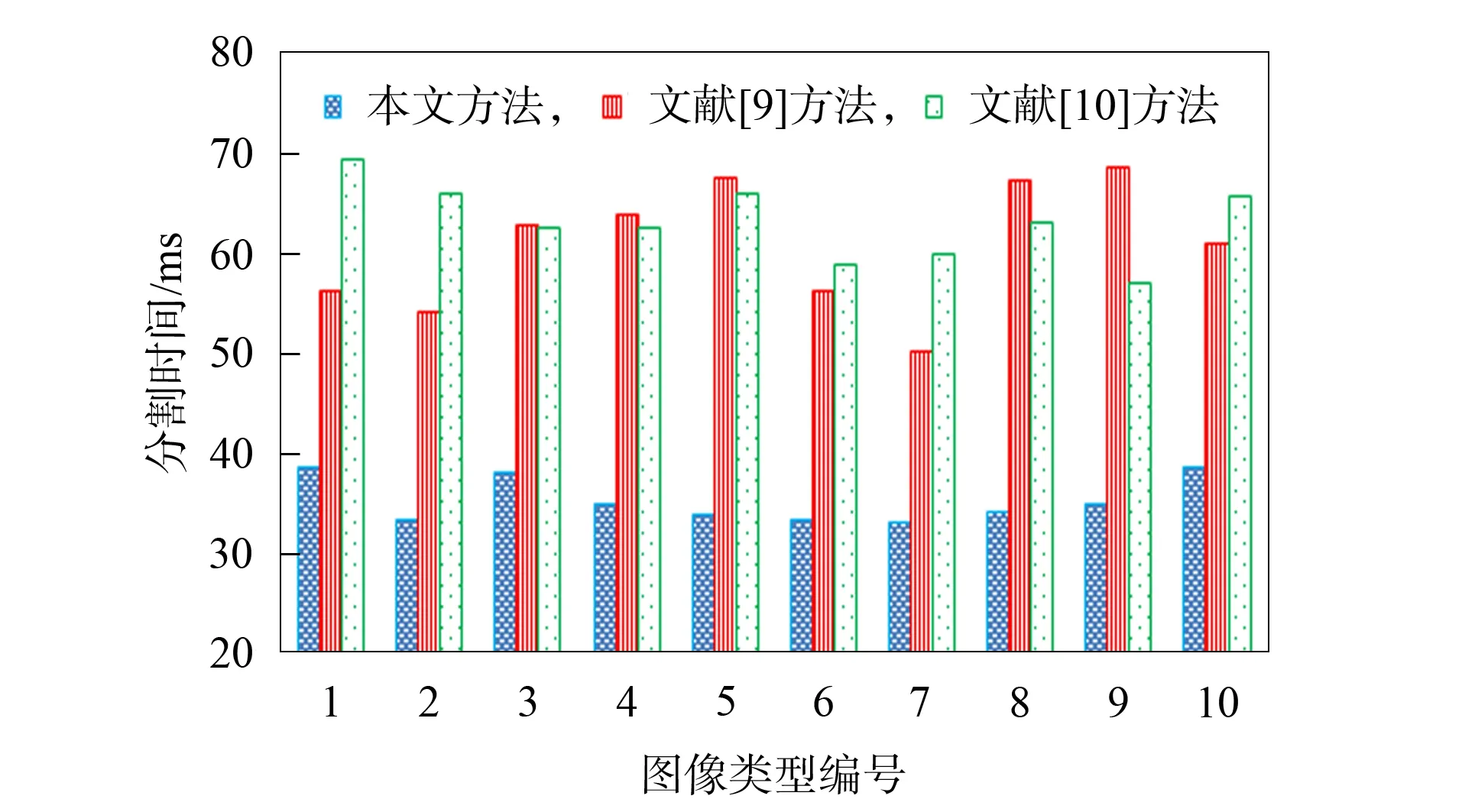
图5 不同方法的图像分割时间对比Fig.5 Comparison of image segmentation time of different methods

2.3.2 图像分割时间对比 统计不同方法分割原始图像的分割时间, 对比结果如图5所示.由图5可见, 本文方法的原始图像分割时间均在40 ms内, 而神经网络方法和深度学习方法的原始图像分割时间均较高, 实验结果表明, 本文方法可快速分割图像, 这主要是由于本文方法融合了粒子群优化算法与活动轮廓波模型的优点, 提升了计算速度, 降低了图像的分割时间.

2.3.3 图像分割区域一致性对比 为更全面地评价图像分割结果, 采用区域一致性[11]评价不同方法的图像分割性能.统计不同方法分割10幅原始图像分割区域的一致性, 结果列于表2.由表2可见, 本文方法10幅原始图像的区域一致性均高于0.9, 神经网络方法和深度学习方法分割10幅原始图像的区域一致性均低于0.9, 本文方法分割图像获取结果与人类视觉分割图像结果基本一致.因此, 本文方法图像分割结果的区域一致性明显优于对比方法, 验证了本文方法的优越性.

综上所述, 本文针对当前粒子群优化算法与活动轮廓波模型的缺陷, 基于组合优化理论, 提出了一种控制活动轮廓演化的快速图像分割方法, 解决了图像分割精度差及计算速度慢等问题.为验证本文方法分割图像的优越性, 将本文方法与神经网络方法、深度学习方法进行仿真对比实验, 实验结果表明, 本文方法分割精度、分割效果、计算速度及抗噪性能等方面均优于对比方法.

表2 不同方法的分割图像区域一致性对比