无刷直流电机转速智能混合控制器设计

王婷婷, 胡黄水, 赵宏伟, 王出航

(1.长春工业大学 计算机科学与工程学院, 长春 130012； 2.吉林大学 计算机科学与技术学院, 长春 130012； 3.长春师范大学 计算机科学与技术学院, 长春 130032)

无刷直流电机(brushless direct current motor, BLDCM)由于具有效率高、可控性好、调速范围宽、功率密度大等优点, 在计算机外围设备、工业控制、航空航天、汽车产业、医疗设备和家用电器等领域应用广泛[1-4].如何对其进行准确地转速控制是无刷直流电机要解决的关键问题之一, 目前已有许多研究结果[3-5].传统PID(比例-积分-微分)控制方法是BLDCM控制的主流方法, 其算法简单、可靠性高, 且无需详细的系统动态性知识[5-7].但BLDCM存在各种不确定性和非线性特征, 其PID增益很难确定, 导致系统控制性能下降.文献[8-9]采用神经网络学习方法调整PID增益； 文献[10-11]分别采用粒子群优化和遗传算法自适应修改PID增益参数.仿真结果表明, 这些方法能有效提高算法的动态性能, 但神经网络学习算法较复杂, 需要较大的存储空间, 粒子群优化和遗传算法初始种群规模的不确定易导致局部最优解.模糊逻辑控制直接运用语言规则, 可完全不依赖被控对象的数学模型, 具有反应速度快、鲁棒性好等优点.文献[12]采用模糊逻辑控制器调整PID增益, 计算量小, 控制效果良好, 但其采用固定缩放因子, 适应能力较差.

为充分利用传统PID和模糊控制器各自的优点, 本文设计一种智能混合控制器(intelligent hybrid PID, IHPID), 通过开关函数根据转速误差在稳态的PI控制器和瞬态的自适应模糊PID控制器(adaptive fuzzy PID, AFPID)之间灵活切换.控制过程引入开关函数, 根据速度误差判定系统所处暂态或稳态, 根据不同状态自动选择最佳控制器, 从而实现最优控制.特别地, AFPID由两级模糊逻辑控制器(fuzzy logic controller, FLC)构成, 其中FLC1完成对PID增益动态调节, FLC2完成对FIC1的缩放因子进行调整， 并对模糊推理的论域进行调节, 使控制器具有较好的控制效果.为验证IHPID的性能, 在空载、负载、转速变化条件下对其进行仿真测试.

1 无刷直流电机数学模型

将电机的三相电流作为状态变量, 以无刷直流电机的基本原理为依据, 则三相绕组电压方程为

(1)

其中：ua,ub,uc分别表示电机三相绕组的相电压；Ra,Rb,Rc分别为电机三相绕组的相电阻；La,Lb,Lc分别为电机三相绕组的自感；Lab,Lac,Lbc,Lba,Lca,Lcb分别为三相定子绕组间的互感；ia,ib,ic分别为电机三相绕组的相电流；ea,eb,ec分别为电机三相绕组的相反电动势.在无刷直流电机中,Ra=Rb=Rc=R,R为绕组的相电阻；La=Lb=Lc=L,L为绕组的自感；

Lab=Lac=Lbc=Lba=Lca=Lcb=M,

M为定子绕组间互感.式(1)可表示为

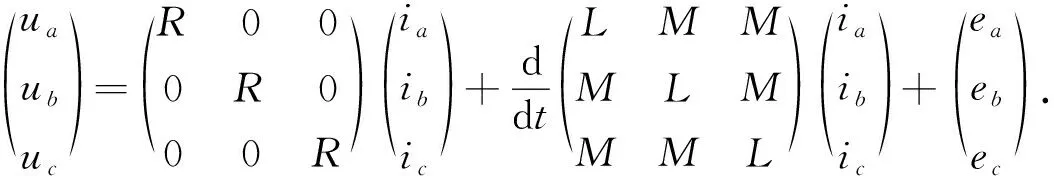
(2)

在对称Y型连接的三相绕组中：

ia+ib+ic=0,

(3)

则

Mia+Mib+Mic=0.

式(2)可简化为

(4)

定子绕组产生的电磁转矩方程为

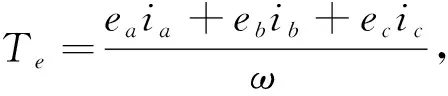
(5)

其中：ω为电机机械角速度;Te为电磁转矩.定子绕组感应电动势为

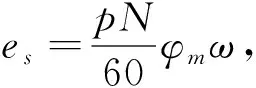
(6)

其中:p为电机极对数;N为总导体数;φm为主通磁.令Ke=(pN/60)φm, 则e=Keω, 其中Ke为电势系数.故电机的电磁转矩方程为

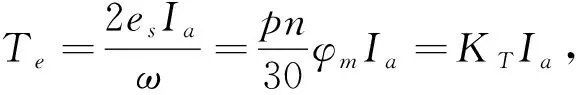
(7)

其中KT为转矩常数.电机运动方程为

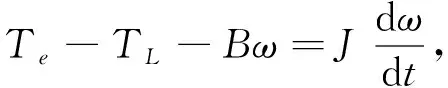
(8)

其中:TL为负载转矩;B为阻尼系数;J为转动惯量.

2 IHPID控制器的设计

2.1 结构设计与分析

为融合传统PI和模糊PID的优点, 本文采用切换函数进行动态切换, 稳态时启动传统PI控制器, 瞬态时启动AFPID控制器, 其结构如图1所示.于是系统可智能地线性调节参量, 从而提高系统动态性能, 同时增强其抗干扰能力.

图1 IHPID控制器结构框图Fig.1 Structure block diagram of IHPID controller

由图1可见, 目标转速ωref输入IHPID, 通过切换函数选择PI或AFPID获得控制信号uPID,uPID输入无刷直流电机, 得到实际转速ωm.AFPID采用两级模糊逻辑控制器, FLC1采用的模式为两输入三输出, 输入为转速误差e和误差变化率ec, 输出为PID增益变化ΔKP,ΔKI,ΔKD.采用重心法对输出参量进行模糊化处理, 重心法使微小的输入变化映射到输出有较大变化, 通过该变化可提高系统的稳定性和灵敏度.FLC2用于自动调节FLC1的缩放因子u1,u2,u3, 以降低超调, 减少沉降时间.根据图1的结构, 控制信号uPID为

(9)

其中：ω为切换函数运行时的转速误差临界值(单位r/min);uAFPID为AFPID控制器运动状态下的控制信号;uPI为PI控制器运动状态下的控制信号.

当转速误差大于ω时,uAFPID执行系统控制:

(10)

因为FLC1输出为PID增益变化ΔKP,ΔKI,ΔKD, FLC2用以调解FLC1的缩放因子u1,u2,u3, 所以uAFPID为

(11)

其中

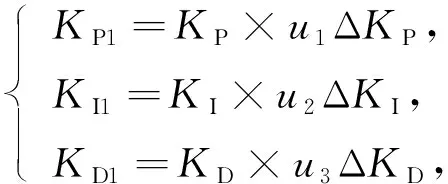
(12)

式中:KP,KI,KD分别为AFPID控制器初始比例、积分、微分增益;KP1,KI1,KD1分别为AFPID控制器自适应调整后的比例、积分、微分增益.当速度误差小于ω时,uPI执行系统控制:

(13)

其中KP2,KI2分别为PI控制器比例、积分增益.

2.2 模糊控制器设计

本文的FLC1和FLC2采用相同的模糊策略, 模糊控制器的输入量为转速误差e和误差变化率ec, 输出量为PID增益变化ΔKP,ΔKI,ΔKD及u1,u2,u3.将误差e和误差变化率ec变化范围定义为模糊集上的论域:

e,ec={-3,-2,-1,0,1,2,3},

(14)

其模糊集为e,ec={NB,NM,NS,ZE,PS,PM,PB}, 分别表示负大、负中、负小、零、正小、正中、正大, 其隶属度函数分别如图2和图3所示.

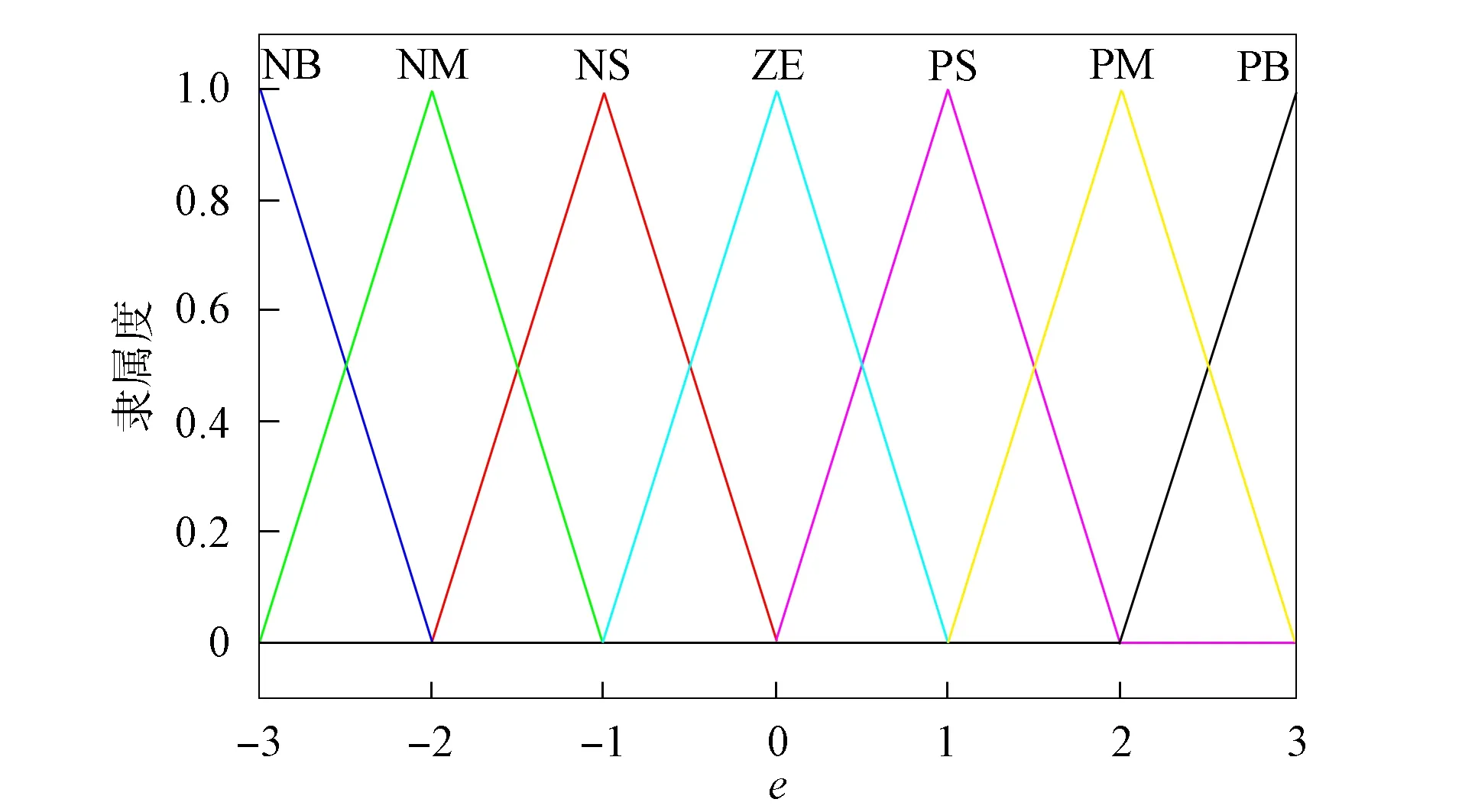
图2 误差e的隶属度函数图像Fig.2 Membership function graph of error e

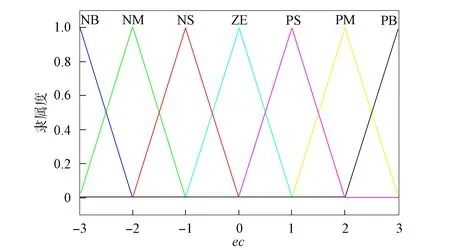
图3 误差变化率ec的隶属度函数图像Fig.3 Membership function graph of error change rate ec

为了按一定的模糊规则进行模糊推理, 本文还需事先确定PID控制器参数的ΔKP,ΔKI,ΔKD模糊规则.定义其模糊论域为

其模糊集为ΔKP,ΔKI,ΔKD,u1,u2,u3={NB,NM,NS,ZE,PS,PM,PB}.模糊规则的建立既参考了专家经验, 也通过多次仿真进行修改.不同模糊论域的模糊规则列于表1～表3.

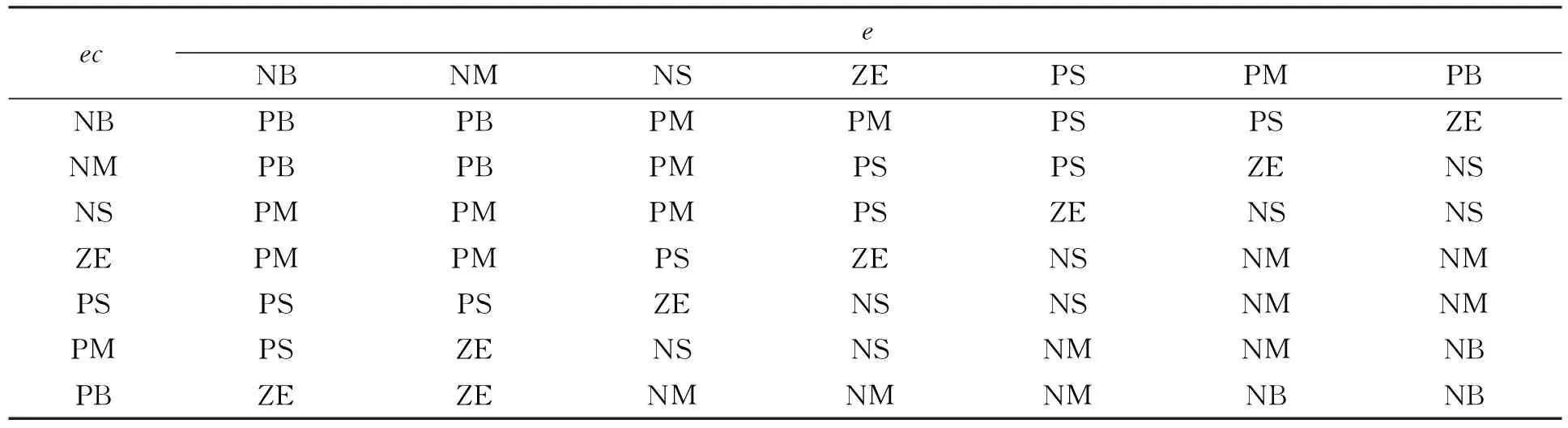
表1 ΔKP,u1的模糊规则

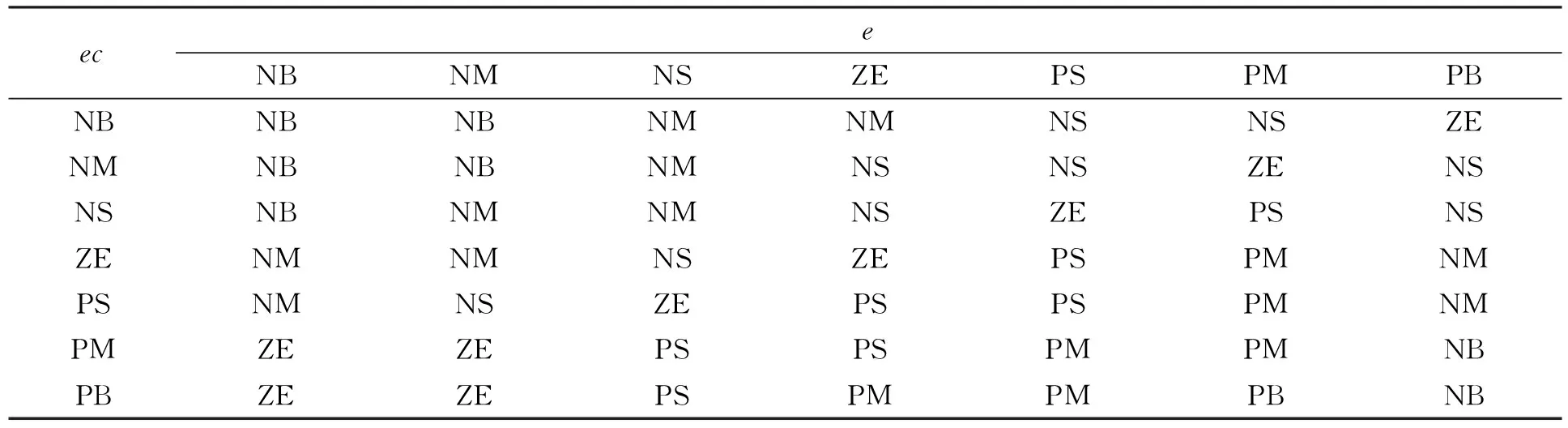
表2 ΔKI,u2的模糊规则

表3 ΔKD,u3的模糊规则

3 仿真分析

图4 无刷直流电机转速控制系统的仿真模型Fig.4 Simulation model of speed control system of brushless DC motor

在MATLAB/Simulink环境下, 建立无刷直流电机转速控制系统的仿真模型, 其结构如图4所示, 其中： 图4(A)为无刷直流电机转速控制系统的仿真模型； 图4(B)为IHPID控制器结构.基于该模型, 对传统PID、模糊PID和IHPID进行性能测试.电机参数[13]: 额定电压为500 V, 额定功率为1 kW, 额定转矩为0.22 N·m, 磁极对数为5对, 反电动势系数为0.048 2 V·S/r, 相电感为1.19 mH, 阻尼系数为4.53×10-6N·m·S/r.首先在空载状态下, 给定电机输入转速ωref=2 500 r/min, 对传统PID、模糊PID和IHPID的转速响应性能进行测试, 结果如图5所示.由图5可见, 传统PID控制的超/欠调量较大, 收敛时间较长,t1≈0.015 s; 模糊PID响应速度较慢, 收敛时间最长,t2≈0.05 s, 也存在轻微超/欠调现象; IHPID的控制效果明显优于传统PID及模糊PID, 基本没有超/欠调现象, 响应速度快, 收敛时间最短,t3≈0.005 s, 具有良好的鲁棒性.

图5 空载条件下的转速响应对比Fig.5 Comparison of speed response under no-load condition

在0.15 s时给系统添加5 N的负载, 测试传统PID、模糊PID和IHPID的转速响应性能, 其结果如图6所示.由图6可见, 传统PID控制在负载改变的情形下, 出现了相对较大的震荡, 且稳态误差大； 模糊PID控制在负载改变的情形下, 出现了明显的超/欠调现象, 但最终恢复到目标转速； 而IHPID能快速恢复到目标转速, 表明其具有较强的自适应能力和抗干扰能力.

图6 负载条件下的转速响应对比Fig.6 Comparison of speed response under load conditions

图7 转速变化条件下的转速响应对比Fig.7 Comparison of speed response under condition of speed variation

为了测试转速跟踪能力, 在转速变化条件下对传统PID、模糊PID和IHPID的速度响应性能进行测试, 结果如图7所示.由图7可见, 传统PID控制在转速改变的情形下有明显超/欠调情况, 且稳态时转速误差较大, 适应能力较弱; 模糊PID响应速度较慢, 也存在轻微超/欠调现象; 而IHPID由于具有较强的自适应能力, 在转速改变的情况下能快速达到新目标转速, 实现转速跟踪.

综上所述, 本文基于对无刷直流电机高精度转速控制的研究, 提出了一种新型的智能混合控制器IHPID, 融合传统PI和自适应模糊PID的优点, 实现了稳态和瞬态转态下转速的最优控制.仿真结果表明, 与传统PID和模糊PID相比, IHPID无论是在空载、负载还是转速变化的条件下, 其转速响应速度、稳态误差及超/欠调量等性能均表现最佳, 具有良好的鲁棒性、抗干扰性和动态适应性.