城市住房价格局部线性地理加权回归分析——以湖北省黄石市为例

王新刚， 孔云峰

（河南大学环境与规划学院，河南 开封 475001）

城市住房价格局部线性地理加权回归分析
——以湖北省黄石市为例

王新刚， 孔云峰

（河南大学环境与规划学院，河南 开封 475001）

研究目的：以土地稀缺、资源组团型城市——湖北省黄石市为例，尝试引入局部线性地理加权回归（LLGWR）方法，探索住房价格及影响因子的空间变化规律，为政府房地产市场管理和土地利用规划提供借鉴。研究方法：整理1.93×104个住房样本和398个楼栋样本，遴选楼栋总层数、容积率、绿化率、小区等级、距区域中心距离、销售年份等作为解释变量，采用LLGWR方法构建城市住房价格的模型，并进行分析与解释。研究结果：与常规线性回归（OLS）相比，地理加权回归（GWR）和LLGWR能更合理和准确地解释住房价格的空间变异，且LLGWR优于GWR；销售年份、容积率、地理区位能显著影响住房价格，同时楼栋总层数、绿化率等因素影响住房价格，且在不同功能片区具有明显差异。研究结论：LLGWR模型可以实现系数函数和误差方差的无偏估计，提高模型的估测精度，能更为准确地解释住房价格；宏观市场趋势是影响住房价格的关键因素，但在不同的地理区位，住房价格增长趋势有明显的差异；土地利用规划和土地供应影响房地产空间分布，但研究区内土地价格对住房价格的影响不明显。

不动产价格；住房价格；局部线性地理加权回归（LLGWR）；黄石市

1 引言

住房作为不动产，其价格是社会关注度最高的热点问题之一。分析和预测住房价格的空间分布和变化趋势是居民、投资者、开发商以及政府管理部门关注的重要问题[1]。住房价格与住房特征要素相关，与市场供给和社会消费水平相关，也受到国家和地方土地供应等政策因素影响[2-3]。土地要素作为城市房地产的重要构成部分，与住房价格具有密切的联系[4]。土地供应能够影响市场预期而引起房价的变化[5]；住宅价格与土地价格相互影响，互为因果[6]。

而从地理空间的角度，土地利用和城市规划引起城市居住空间结构向多核、分散组团发展[7-8]，区位是影响住房价格的一个关键因素。因住房价格在空间邻域上的相关性和异质性，在统计上具有非平稳性，通常采用地理加权回归（GWR）模型进行区位分析[9]。通过对价格和相关的影响因素进行回归统计，探测区位因素对价格的影响机制[10-12]。

然而，GWR本质上属于Nadaraya-Watson核估计统计方法，存在边界效应[13]。模型的回归系数是空间地理位置的函数，与一维区间相比，边界效应更为剧烈，使得边界区域的估计容易失真，从而导致分析结果偏离实际情况。Wang等[14]提出局部线性地理加权回归（LLGWR）方法，较好的解决了边界效应问题。目前该模型仅在数学领域进行了理论证明，尚未有实证分析的文献报道。本文尝试将LLGWR方法引入城市住房价格空间分析，以土地稀缺、典型组团型城市——湖北省黄石市为例，探索并解释城市住房价格及影响因子的空间变化规律，为政府部门管理房地产市场，做好土地开发和利用提供科学参考。

2 LLGWR方法的概念

GWR是建立在空间相关性和空间异质性假设前提下的局部回归分析，具有概念上的简单性和实现上的易操作性。设Y为因变量， X1，X2，…，Xm为自变量，（Yi；X1，X2，…，Xm）表示因变量和自变量在地理位置（ui，vi）处的观测值（i=1，2，…，n ），GWR模型基本公式为：

式1中，回归系数αk（u, v）（k=0，1，2，…，m）是地理坐标（u，v）的函数。残差εi（i=1，2，…，n）为独立同分布的误差项，服从正态分布且E（εi）=0，Var（εi）=σ2。

采用局部线性拟合方法，将系数函数局部展开为地理坐标的线性函数，可将GWR模型扩展为局部线性GWR模型（LLGWR）。

记Xi=（Xi1，Xi2，…，Xim）T是自变量的第i组观测值构成的列向量，X=（X1，X2，…，Xn）为因变量矩阵。在给定区域内任一点（ui，vi），设wi（ui，vi）为（ui，vi）点的第i个权重值，wi（ui，vi）=Diag（w1（ui，vi）, w2（ui，vi），…，wn（ui，vi））表示点（ui，vi）的空间权重矩阵。

令：X（ui，vi）=

则帽子矩阵为：

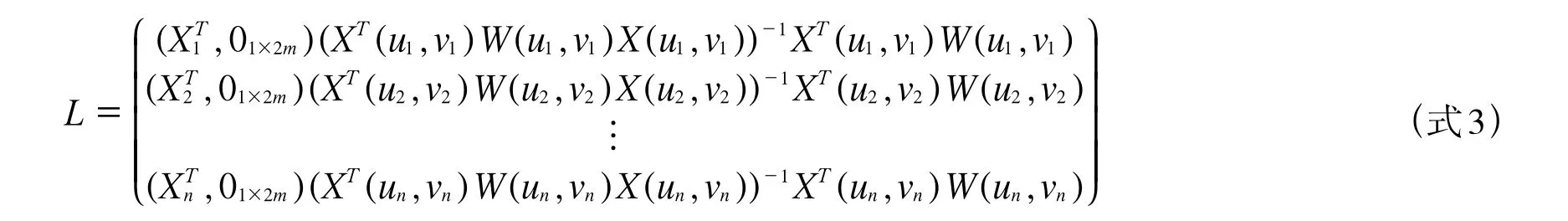
因变量Yi=（Y1，Y2，…，Yn）T在n个观测点处的拟合值为：

与GWR模型一样，空间权重矩阵W（ui，vi）表示对于地理位置（ui，vi），（uj，vj）参数估计的重要性，（uj，vj）与地理位置（ui，vi）越近，权重越大。有两种常见的方法构建空间权重矩阵：固定核和自适应核。对于固定核，距离是固定的，而邻近样本的数量是变化的。对于自适应核，距离是变化的，而邻近样本的数量是固定的[9]。

通常采用高斯距离衰减函数确定空间权重，如式5。式5中wij表示点（uj，vj）和点（ui，vi）之间的权重，dij表示点（uj，vj）到点（ui，vi）的欧氏距离，h是带宽参数。 固定核的带宽h是在均值与方差之间平衡的一个参数，如果h值过大，就趋向于全局模型；如果h值太小，系数估计的方差很大。

若空间数据分布不均匀，为避免数据稀疏的区域扩大空间的异质性或数据密集的区域掩盖了敏感的空间异质性[9]，自适应核能够根据数据分布情况，选取数量相同的最邻近点，自适应调整带宽，从而在数据点密集的地方减小带宽，在数据点稀疏的地方增加带宽。例如，bi-square权重函数如式6。式6中hi表示第i个观测点（ui，vi）的带宽。

回归系数的估计依赖于带宽参数h的选择，最优带宽参数可根据AICc准则确定[15]，如式7。此处，σˆ是随机误差项的极大似然估计，设SSE表示残差的平方和，近似的取σˆ2=SSE/( n -tr( L))，t（rL）是帽子矩阵L的迹。当AICc值最小时，相应的h即是最佳的带宽。

局部线性回归（LLGWR）方法在广泛的系数函数类型下，可以得到系数函数和误差方差的无偏估计[16]，因而改进了GWR方法，能够提高模型估计精度。

3 研究区域及样本数据

黄石市位于湖北省东南部，长江中游南岸，是武汉城市圈副中心城市，中国中部地区重要的原材料工业基地。全市下辖黄石港区、西塞山区、下陆区、铁山区及团城山经济技术开发区（图1），市区面积226 km2，人口78×104人。黄石市是典型的资源组团型城市，地形较为复杂、土地稀缺，具有区域分散、多中心的空间结构特点；依据地形条件、传统产业布局和近年土地规划，城区发展采用中心组团式布局：铁山区、下陆区和西塞山区为工矿区；黄石港区南部为商业中心区，北部为花湖物流中心区；团城山区北部沿湖为行政中心区，山南为经济技术开发区。受城市和土地利用规划影响，该市房地产市场主要集中分布在黄石港区和团城山区。

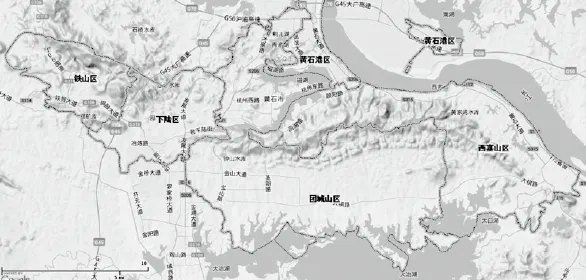
图1 研究区地形图Fig.1 The topographic map of study area

本文数据来源于黄石市房地产局新建商品房网签备案系统。选择2007—2012年的商品住宅成交价格数据1.93万个（铁山区无数据）。为便于作整体分析，按楼栋计算平均住房单价，共获得398个楼栋样本点。依据黄石市城区综合用地级别图（2008年）并结合城市规划，将研究区划分为4个区域：黄石港区南部商业区、黄石港区北部花湖物流区、团城山开发区、下陆区老工业区，选择各区域中土地级别最高的地块中心为区域中心点。

针对样本数据进行相关分析，发现价格与主要销售年份、楼栋总层数、容积率、小区等级、绿化率呈现或强或弱的线性相关关系；而研究区土地成交价影响住房价格变化的相关性很弱，原因可能在于开发商从获得土地到楼盘销售的周期较长，也有部分开发商有意囤积土地。运用探索性空间数据分析，住房价格的Moran's I为0.19，具有较强的空间正自相关性；聚类和异常值分析（Anselin Local Moran's I），表明住房价格具有局部空间异质性；住房所在区域和区位对价格影响显著。

选择价格解释变量：反映土地稀缺和建筑成本的容积率（PR）和楼栋总层数（FL），反映社区环境的小区等级（CL）和绿化率（GR），反映城市区位属性的住房距区域中心距离（ND），以及反映宏观经济和土地供应等政策变化的销售年份（YI）。

4 回归分析

运用常规线性回归（OLS）方法进行全局模型估计。模型拟合度R2=0.49，能合理解释49%的住房价格变化原因。模型的F检验值为75.88，其相应的概率为0.00＜0.05，表明通过显著性水平为0.05的F检验；除距区域中心距离外，各回归系数t检验值均大于3，各回归系数的置信水平均为95%以上，表明各回归系数与住房价格的线性关系显著。同时，计算各自变量的方差膨胀因子进行检验[17]，发现自变量VIF值均小于2，远小于10，表明变量间的多重共线性现象较弱，适合于OLS模型分析。

回归结果也表明：黄石市住房价格可以由住房的本身属性、环境因素、区位属性和时间因素来建模；住房价格与容积率、销售年份、楼栋总层数、小区等级、绿化率成正相关关系，而与住房距区域中心距离成负相关关系；小区等级和销售年份与住房价格有着同方向的紧密联系；非常特殊的是，与其他城市不同，研究区内土地稀缺，开发强度较大，容积率越高，住房价格反而越高。不过，OLS模型只是提供全局平均意义上的一定程度上的解释，尚有51%的住房价格的变化未能解释，部分原因在于全局模型是假设在空间内住房价格的持续变化是平稳的，而实际上其变化具有非平稳性[9]。

研究区住房均价分析表明，在样本区域住房的分布是不均匀的：在靠近4个中心区域密度大，向外围区域密度低；住房均价的空间分布也是非均质的，即具有空间的异质性：在4个区域，靠近中心位置的住房均价普遍高于外围区域。样本数据特征表明，地理加权回归分析适合于全市住房价格分析。由于空间的异质性，变量之间的关系是随空间位置的变化而变化的，OLS模型并未考虑这种变化特征，进一步利用GWR模型进行局部统计分析。

因样本数据空间分布的非均质性，采用bi-square自适应核函数，避免了某些样本点的邻近样本数据稀疏而造成的估计偏差[9]。GWR模型估计结果如表1，模型的拟合度R2为0.82，与OLS模型的拟合度相比，有大幅度的提高，说明模型描述的回归关系具有空间非平稳性；AICc值作为模型拟合显著性的标识，由OLS模型的6388下降到GWR模型的6262，减少了126，远大于3[9]，表明GWR模型改进回归的拟合度是十分显著的，即使增加了计算复杂性，GWR模型也优于OLS模型。同时，GWR模型的统计检验F值为1.44，相应概率P值为0.00＜0.05，小于给定的显著性水平0.05，GWR模型拟合黄石市的住房均价，明显优于OLS模型，住房均价与影响因素之间的整体关系确实存在显著的空间非平稳性。

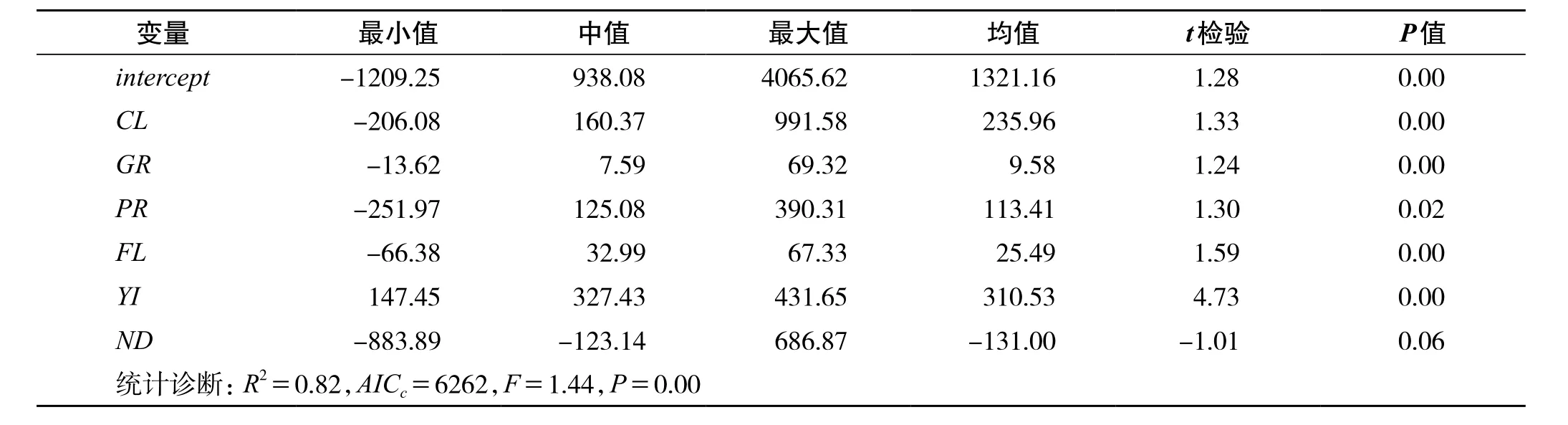
表1 GWR模型回归系数的估计结果Tab.1 The estimation results of GWR regression coeffcient

考虑到研究区域地形特殊，山体和湖泊众多，4个区域空间边界复杂，进一步利用LLGWR模型进行局部统计分析。采用三阶距χ2逼近方法计算，检验LLGWR各回归系数变化的显著性[18]。模型估计结果如表2，检验统计量F值为3.22，与之相应的显著性检验概率P为0.00＜0.05，模型通过显著性水平为0.05的F检验。各回归系数t检验的显著性概率P值为0.05，通过显著性水平为0.05的t检验，表明各回归系数随空间位置的变化具有显著性。同时，与GWR相比，LLGWR方法将AICc值减小34；拟合度R2由0.82提高到0.87；F统计值由1.44提高到3.22；这些表明LLGWR优于GWR。

5 LLGWR结果分析

LLGWR回归系数反映了各解释变量的空间变异状况。因所有系数均接近正态分布，将系数标准化，并按0.5的间隔进行分类，在GIS软件中制作系数空间分布示意图。

研究区土地规划具有多中心的空间结构特点，城市区位是影响住房价格的重要因素。距区域中心距离的远近一定程度上反映了住房用地级别的不同，与住房价格具显著的负相关性（图2）。楼栋到区域中心距离每增加1 km，住房价格平均减少74.18元/m2。当然，同一小区楼栋到区域中心距离相差较小，住房价格受此影响较小，图3中差异不明显；而不同小区楼栋受距区域中心距离的影响较大。

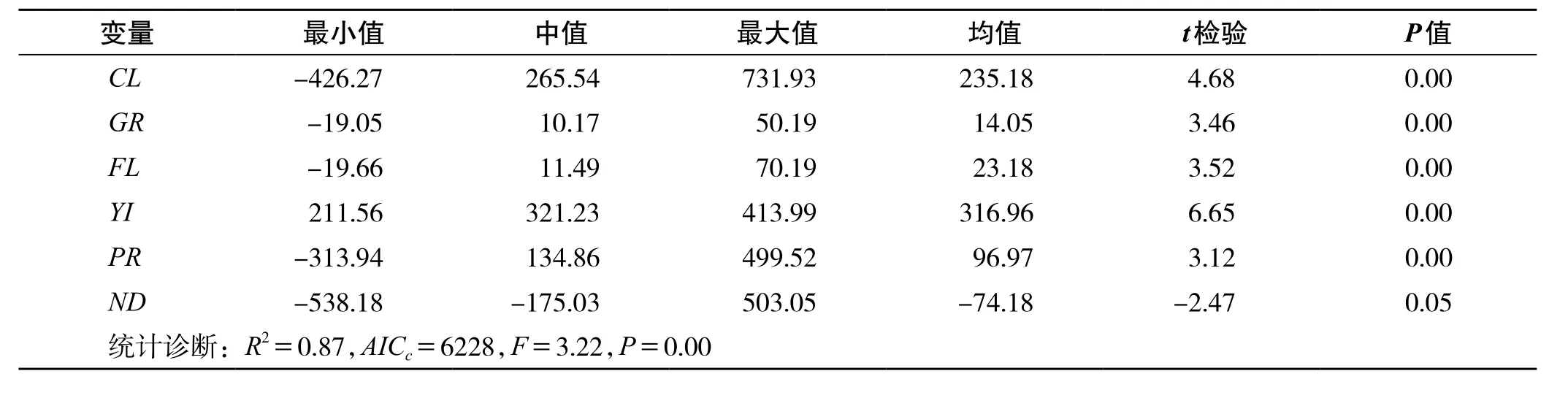
表2 LLGWR模型回归系数的估计结果Tab.2 The estimation results of LLGWR regression coeffcient

受宏观经济趋势和土地供应等政策变化影响，销售年份是影响研究区住房价格的重要时间因素，两者之间具有较强的正相关性。时间每递增1年，住房价格平均增加316.96元/m2。同时，销售年份对住房价格的影响具有空间非一致性（图3）。在西塞山区和黄石港区靠近湖边和江边位置，住房价格上升幅度大。原因在于近两年黄石市江滩和磁湖治理具有成效，使靠近江边和湖边的楼盘环境得到改善，价格增幅比较显著。

小区等级代表小区的档次定位，与小区规模、楼盘品质、配套服务设施等相关，与住房价格之间具有正相关性。小区等级数每上升1，住房价格平均升高235.18元/m2。小区等级对住房价格的影响具有显著的空间非一致性（图4）：在商业或行政中心核心片区，小区等级对住房价格影响较小；在城市中心的外围片区，对住房价格影响比较大。原因在于城市中心区区位优势是影响住房价格的主要因素，而在外围地区，住房要依靠住宅小区品质和档次提升价格。

绿化率是居住区用地范围内各类绿地的总和与居住区用地的比率，其高低在一定程度上反映居住环境的质量，也是影响住房价格的因素之一。绿化率提高1%，住房价格平均提高14.05元/m2。绿化率对住房价格影响分布见图5，回归系数的估计值在空间上呈明显的变化。靠近市中心位置，绿化率对住房价格影响很小；在离市中心较远位置，其对住房价格有较大影响。在局部片区，其对住房价格影响十分显著，如黄石港区华新水泥厂和黄石火电厂、西塞山区作为工矿区对环境有负面影响，从而造成住房价格随绿化率的变化而有明显的变化。

楼栋总层数与住房价格具有一定的正相关性。楼栋每增加1层，住房价格平均增加23.18元/m2。黄石市的住房用地供应紧张，高层住宅或超高层住宅是发展的方向；而楼栋总层数增加，也意味着住房建筑成本的增加，其回归系数估计值在空间上显著变化（图6）。在距离市中心较远位置，楼栋总层数对住房价格的影响比较显著；而在靠近市中心位置，影响比较小，其原因估计是靠近市中心位置，楼栋总层数普遍都比较高，而偏离市区位置，高层住宅较少，其成本对住房价格影响比较明显。

通常来说，随建筑容积率增加住房价格降低。但在黄石市，容积率与住房价格整体上呈现正相关性，容积率增加1.0，住房价格平均增加96.97元/m2。原因可能是土地资源紧缺，多数住宅设计为高层建筑，在提高容积率的同时建筑成本增加。同时，容积率回归系数在不同片区差异显著（图7）：距离市中心较近片区，容积率对价格影响小，偏远位置尤其是团城山开发区、花湖新区，容积率显著的影响住房价格，其原因是偏远位置小区，建设高层住宅提高容积率，造成房屋成本增加，促使住房价格有明显的升高。

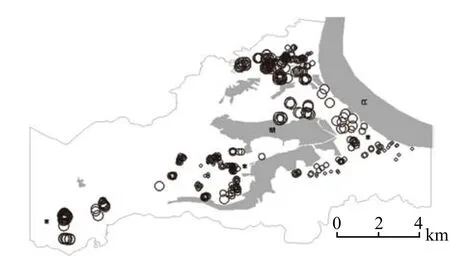
图2 距区域中心距离系数估计值的分布图Fig.2 The distribution map of coeffcient estimates on distance from the regional centre

图3 销售年份系数估计值的分布图Fig.3 The distribution map of coeffcient estimates on sales year

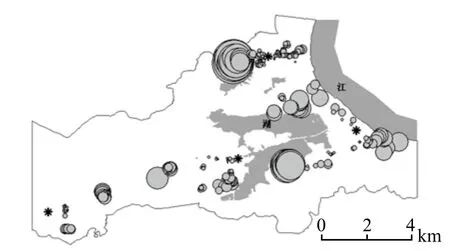
图4 小区等级系数估计值的分布图Fig.4 The distribution map of coeffcient estimates on cell level

图5 绿化率系数估计值的分布图Fig.5 The distribution map of coeffcient estimates on greening rate

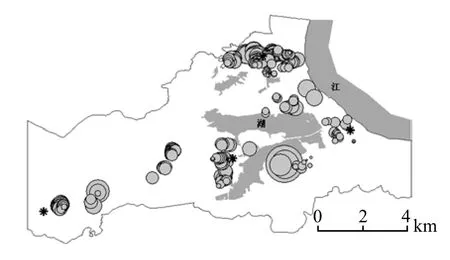
图6 楼栋总层数系数估计值的分布图Fig.6 The distribution map of coeffcient estimates on foors

图7 小区容积率系数估计值的分布图Fig.7 The distribution map of coeffcient estimates on cell plot ratio

6 结论

本文以典型的土地稀缺、资源组团型城市——湖北省黄石市为例，结合其多个片区中心、地形复杂的特点，构建城市住房价格的局部线性地理加权回归（LLGWR）模型，探索了住房价格及影响因子的空间变化规律。案例分析发现：（1）与常规线性回归（OLS）相比，GWR和LLGWR模型采用局部光滑拟合方法，考虑了住房价格的空间异质性，能更为准确地解释住房价格，且LLGWR优于GWR；（2）宏观市场趋势是影响住房价格的关键因素，但在不同的地理区位，住房价格增长趋势有明显的差异；（3）反映土地紧缺的容积率与住房价格具有显著的正相关性，但在不同的功能片区，其影响力具有差异；（4）研究区土地规划具有多中心的空间结构特征，城市区位是影响住房价格的重要因素，两者具有较显著的相关性，在商业中心区和行政中心区，价格受区位影响最为突出；（5）研究区土地供应等政策变化影响房地产空间分布，但土地价格与住房价格之间并无明显的相关关系。

（

）：

［1］ Adair A.S., Berry J.N., McGreal W.S. Hedonic modeling,housing submarkets and residential valuation［J］ . Journal of Property Research, 1996, 13（1）: 67 - 83.

［2］ 阮连法，包洪洁，温海珍.重大事件对城市住宅价格的影响来自杭州市的证据［J］ . 中国土地科学，2012，26（12）：41 - 47.

［3］ 王松涛，刘洪玉.土地供应政策对住房供给与住房价格的影响研究［J］ . 土木工程学报，2009，42（10）：116 - 121.

［4］ Pollakowski H.O.,Wachter S.M. The effects of land-use constraints on housing prices ［J］ . Land Eco-nomics, 1990, 66（3）: 315 - 324.

［5］ 黄忠华，虞晓芬，杜雪君.土地供应对住房价格影响的实证研究——以上海市为例［J］ . 经济地理，2009，29（4）：624 - 627.

［6］ 张娟峰.住宅价格与土地价格的城市间差异及其决定因素研究［D］ . 杭州：浙江大学，2008.

［7］ 廖邦固，徐建刚，宣国富，等.1947—2000年上海中心城区居住空间结构演变［J］ . 地理学报，2008，63（2）：195 - 206.

［8］ 牛俊蜻，吕园，刘科伟.城市规划视角下西安市主城区住宅空间结构演变研究［J］ . 人文地理，2011，26（4）：48 - 53.

［9］ Fotheringham A.S., Brunsdon C, Charlton M. Geographically Weighted Regression［M］ . Chichester, UK: John Wiley and Sons, 2002.

［10］ Yu D. Spatially Varying Development Mechanisms in the Greater Beijing Area: A Geographically Weighted Regression Investigation［J］ . Annals of Regional Science, 2006, 40（1）: 173 - 190.

［11］ 覃文忠，王建梅，刘妙龙.混合地理加权回归模型算法研究［J］ . 武汉大学学报：信息科学版，2007，32（2）：115 - 119.

［12］ McCord M, Davis P.T., Haran M, et al. Spatial variation as a determinant of house price:Incorporating a geographically weighted regression approach within the Belfast housing market［J］ . Joural of Financial Management of Property and Construction, 2012, 17（1）: 49 - 72.

［13］ Farber S, Pá ez A. A systematic investigation of cross-validation in GWR model estimation: empirical analysis and Monte Carlo simulations［J］ . Journal of Geographical System, 2007, 9（4）: 371 - 396.

［14］ Wang N, Mei C.L., Yan X.D. Local linear estimation of spatially varying coefficient models:an improvement on the geographically weighted regression technique［J］ . Environment and Planning A, 2008, 40（4）: 986 - 1005.

［15］ Hurvich C.M., Simonoff J.S., Tsai C.L. Smoothing parameter selection in nonparametric regressi On using an improved Akaike information criterion［J］ . Journal of the Royal Statistical Society B, 1998, 60（2）: 271 - 293.

［16］ 梅长林，王宁.近代回归分析方法［M］ . 北京：科学技术出版社，2012.

［17］ Robinson C, Schumacker R.E. Interaction effects: Centering,variance inflation factor and interpretation issues［J］ . Multiple Linear Regression Viewpoints, 2009, 35（1）: 6 - 11.

［18］ Mei C.L., He S.Y., Fang K.T. A note on the mixed geographically weighted regression［J］ . Journal of Regional Science, 2004, 44（1）: 143 - 157.

（本文责编：郎海鸥）

Local Linear Geographically Weighted Regression Analysis on the Urban Housing Price: A Case Study of Huangshi City, Hubei Province

WANG Xin-gang，KONG Yun-feng
（College of Environment and Planning, Henan University, Kaifeng 475001, China）

This paper aims to analyze the spatial variations of urban housing price and its impact factors using local linear geographically weighted regression （LLGWR） model. For purpose of real estate market management and land use policy making scientifically, Huangshi City, Hubei Province, a typical land-scarce, resource-based and multi-group city, is selected as the study area. Additionally, 193,00 housing units and 398 buildings are collected as modeling samples. Based on the general and spatial statistics, the floor numbers, the plot ratio, the greening ratio, the level of property management, the distance to nearest urban center, and the year of sale are selected as explanatory variables, constructing the model and carries on the analysis and interpretation. The modeling results indicate that, compared with ordinary linearregression （OLS）, GWR and LLGWR are more suitable for interpreting urban housing price, and LLGWR is better than GWR. The housing price is substantially affected by the year of sale, plot ratio and the urban geographic location; and it is also related to the building height and greening ratio. However, they have very different contributions in different urban functional zones. There are three findings from this research: 1） LLGWR model, using unbiased estimation of coefficient function and error variance, can improve estimation and prediction accuracy of the urban housing price; 2） Macro market trend is the key factors affecting the housing price, but in different geographical location, housing price growth trend is obvious difference; 3） The spatial distribution of real estate development is closely related to land use planning and land supply policy, however, the relationship between land price and housing price is not obvious in the study area.

real estate prices; housing price; local linear geographically weighted regression （LL-GWR）; Huangshi City

P208

A

1001-8158（2015）03-0082-08

10.13708/j.cnki.cn11-2640.2015.03.011

2014-04-29

2015-01-12

国家十二五科技支持计划（2012BAJ051306）。

王新刚（1972-），男，河南郑州人，博士研究生。主要研究方向为城市问题和城市住房。E-mail: wuhanwxg@163.com