对两个牵引模型的辨析
2015-01-08 07:10:14周佳
物理教师 2015年1期
周 佳
(江苏省常熟中学,江苏 常熟 215500)
牵引问题是高中物理常见的一类问题,而该类问题中有两个模型非常容易混淆,下面从两个模型各自的结构特点入手,对模型进行辨析与区分.
模型1:如图1所示,滑块A置于光滑水平桌面上,细线一头与滑块相连接,连接点为B,另一头绕过定滑轮,当以速度v拉绳头时,滑块A沿水平面向右运动.
模型2:如图2所示,滑块A置于光滑水平面上与动滑轮相连,一根轻绳绕过两滑轮后固定在C点,动滑轮下方的轻绳水平,当以速度v拉绳头时,滑块A沿水平面向右运动.
问题:求当轻绳BD与水平面夹角为α时,两个模型中滑块A运动的速度分别是多少?
解析:两个模型看上去似乎差异不大,但滑块的速度却是不同的.首先从模型的结构上来分析,模型1中滑块A是与细绳直接相连的,而模型2中滑块A是通过动滑轮与细绳相连的,显然两个模型在连接的方式上是不同的.其次,模型2中由于动滑轮的存在,导致了细绳被分成了上下两部分,因此细绳收缩的距离也就分为了上下两部分.下面利用微元法来分析由于连接方式不同导致的不同结果.在模型1中,令滑块的速度为vA,在Δt(Δt→0)时间内接触点从B运动至B′(如图3所示),由于时间很短,因此该过程可看成是匀速直线运动,故
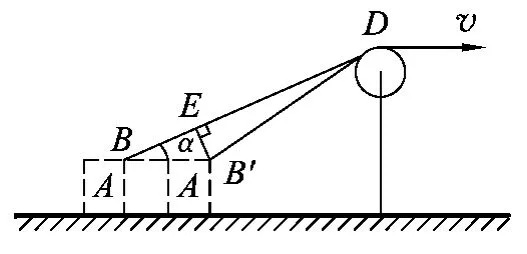
图3

作B′E⊥BD,由于Δt很小,可认为DE=DB′,因此BE的长度就是Δt时间内细绳收缩的长度Δl1,即

在ΔBB′E中,满足

由(1)~(3)式可得


图4
在模型2中,同样令在 Δt(Δt→0)时间内接触点B运动至B′(如图4所示),也可以得 到BB′=vAΔt与BE≈Δl1的关系,不同的是由于动滑轮的运动,BE的长度仅仅是该过程动滑轮上方细绳收缩的长度,而动滑轮下方轻绳收缩的长度为

故细绳总的收缩长度Δl可表示为
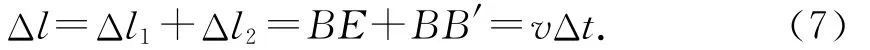
将(1)、(3)式代入(7)式可得
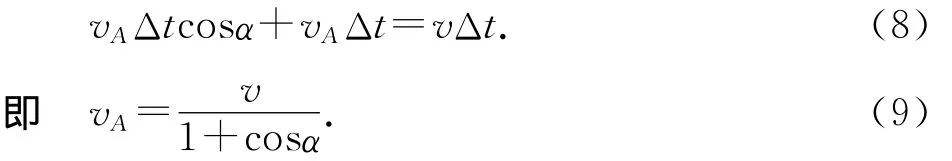
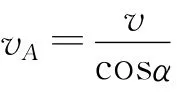
猜你喜欢
中学生数理化·自主招生(2024年1期)2024-05-29 03:43:56
中学生数理化(高中版.高考理化)(2024年1期)2024-01-27 10:18:38
体育科技文献通报(2022年3期)2022-05-23 13:46:52
初中生学习指导·提升版(2020年5期)2020-09-10 07:22:44
决策探索(2019年19期)2019-10-21 09:16:32
数学大王·趣味逻辑(2019年9期)2019-10-09 03:36:36
新世纪智能(教师)(2019年2期)2019-09-11 05:56:40
物理通报(2019年7期)2019-06-29 07:32:56
物理通报(2018年9期)2018-08-31 07:45:58
理科考试研究·高中(2017年7期)2017-11-04 22:09:06

