行星变速器杠杆分析法

黄宗益

（同济大学 上海200092）

前言

行星机构很难直观理解，行星轮系中各齿轮和各构件间的运动关系（各构件的速度和方向，机构的速比）、其传力情况（传力路线和传力比）很难表达，使得很多人感到困惑.过去主要采用数学解析法，将行星轮系转换成数学方程式（我们称为行星机构的数学表示），将行星机构运动学和动力学求解归结为解线性方程式，能很容易地编制程序，通过计算机来求解.但从数学上求得结果容易，理解却很困难，因为物理概念（运动关系和传力情况）不清楚、不直观.工程上问题除了数学表达外，还可以用和人的视觉直接相连的几何图形来表达，行星机构的几何表达就是杠杆分析法.将行星轮系转变为杠杆系来进行理解和分析，两者在运动学和动力学的数学关系式上是完全相同的，但将这些看不懂的行星轮系转换成能直观理解的杠杆系来进行分析，就比数学法来得直观、形象、快速、简单和明了，能一下子掌握其实质性的概念.为说明杠杆分析法的具体应用，在这里我们以一个具体复杂的轿车行星变速器（ZF公司新开发应用于轿车上的ZF8行星变速器）为例来介绍行星变速器杠杆解析法.

1 ZF8行星变速器的传动简图和杠杆图

ZF8行星变速器为4行星排组成的8挡变速器，仅采用5个结合元件（3个离合器2个制动器），结构简单紧凑挡位数多，挂挡時5个结合元件中3个结合元接合，仅2个结合元件空转，传动效率高，是个优秀設计产品，广泛用于新型轿车上。

1.1 首先将行星机构传动简图（图1）转换成杠杆图（图2）：

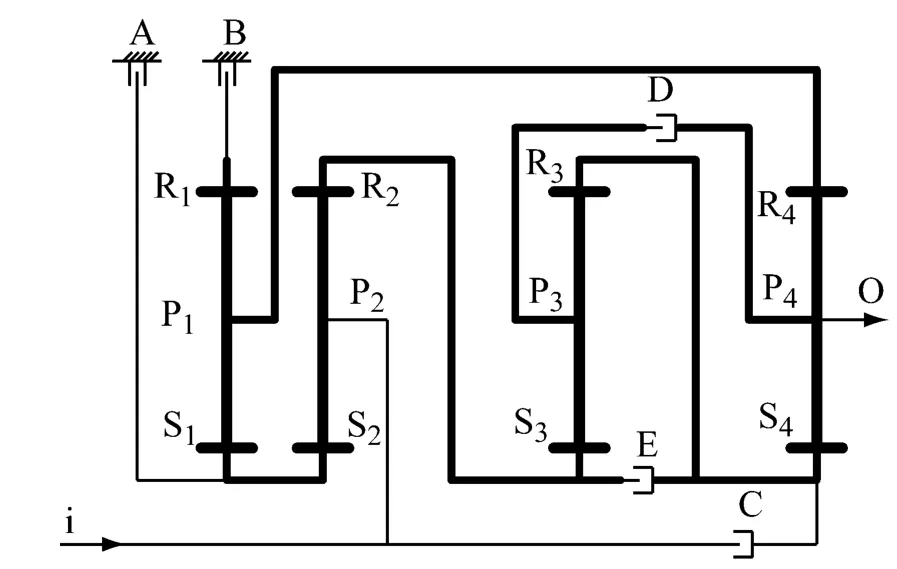
图1 行星机构传动简图Fig.1 Planetary transmission diagram

1）将每个行星排画成一个杠杆，杠杆上有三个点分別代表：R—齿圈；P—行星架；S—太阳轮.

2）画行星排构件间连接线：S1—S2；P1—R4；R2—S3；R3—S4.

3）画结合元件：制动器：A、B；离合器：C、D、E.注意：画行星变速器的杠杆图只要杠杆连接关係相同和结合元件布置位置相同，可以画成不同形式。因此为了便于理解变速器，我们就画成2种杠杆图形式（如图2所示）。

图2 行星变速器杠杆图Fig.2 Planetary transmission lever diagram

1.2 各档结合元件状态表：见表1

表1 各档位结合元件接合状态

2 各档传动杠杆图

为了清楚地表达各个档位的行星机构运动和传动情况，画出了各档传动杠杆图（在該档传动中不起作用的行星排在图中沒有表示）。

2 行星变速器转速分析

分析和设计行星变速器，需要知道各档位下行星齿轮机构中每一构件和每个行星轮的转速，处于分离状态各结合元件的相对转速.下面以最复杂的第5档为例说明转速分析作图方法：

（1）各档等效杠杆转速线图和各构件的转速

应該说明行星变速器挂挡接合时，整个行星变速器就合併成为1个杠杆，各构件的转速可用直角坐标系XOY来表示。挂第5档时行星机构合併成为6支点杠杆（6个节点分别代表行星变速器杠杆图上的6个独立构件.：①代表S2、S1构件，②代表P2、R3、S4构件，③代表 P3、P4构件，④代表 P1、R4构件，⑤代表R2、S3构件，⑥代表R1构件），如图4所示。

设X＝1平行Y轴的垂直线上输入构件①的转速点为＋1，在Y轴上构件⑥代表固定点，连接此两点得挂第5档时杠杆的转速线，我们称为等效杠杆转速线图。其上各支点的X坐标值的大小和正负分别代表该构件转速的大小和方向，X坐标为正表示该构件的转速与输入构件转向一致，为负则表示该构件转向相反.从等效杠杆转速线图我们就很容易知道了各构件大致的转速大小和方向。

（2）各档位下各结合元件相对转速

在某一档位下，分离状态的结合元件（制动器和离合器）的相对转速可由组成该结合元件的两个基本构件的转速差求得.

例如，挂5档时求离合器E的相对转速.离合器E布置在构件R2和构件R3之间，从图中可知5档时构件R2转速为a点X坐标值，构件R3转速为b点X坐标值，其相对转速的大小可用线段ab的长度来表示.

对于处于分离状态的制动器A，布置在构件S1和固定的箱体之间，所以其相对转速就是该构件的转速.其相对转速的大小可用线段cd的长度来表示.

图3 各档位等效杠杆图Fig.3 The equivalent lever diagram for each gear

图4 第5档等效杠杆转速线图Fig.4 5th gear lever equivalent speed chart

（3）各档位下各行星排行星轮的相对转速

以第5档求行星排1的行星轮（相对行星架）的转速为例，来说明求行星轮转速的作图方法：

作行星排1的行星轮PG1的转速线：过行星架（P1）构件点④的转速点作Y轴的平行綫，沿Y轴向上离④点距离为ZR1/ZPG1求得行星排1的行星轮构件转速点f（对于标准齿轮和高度变位齿轮传动，该距离可取2K1/（K1－1））.过f点作平行于X轴的线，与5档转速綫交于e点，则的长度代表了该档位下行星排1的行星轮PG1的相对转速的大小如与X轴方向一致则为正.

同理，可求得5档时其他各行星排行星轮的转速的大小和方向（分別为PG2、PG3、PG），如图4所示.

（4）以第5档为例来说明用杠杆法来求速比计算公式的方法：

用杠杆法来求速比实际上就是求几何杠杆比，我们可以直接在杠杆图上求得速比计算公式。选其中一个杠杆（例如以第4行星排为基准尺度，a＝1）作为起点，来统一传动杠杆图上各杠杆比例尺度，例中以第四行星排为起点，不用复杂计算，就可以依次推导求得第三、二、一行星排（各杠杆）上的各段尺寸（用包含行星排特性参数k的表达式来表示，标注在各杠杆的线段上.如图5和表2所示。

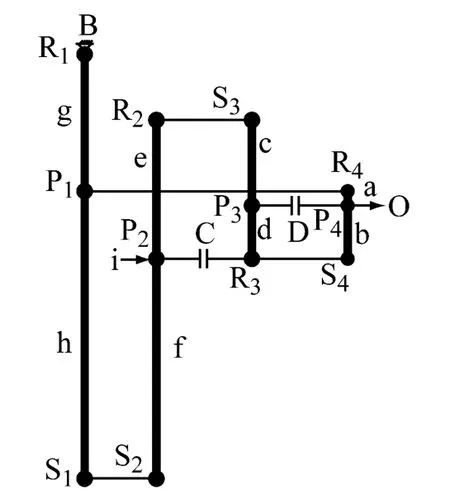
图5 杠杠法求速比图Fig.5 Ratio diagram of lever method

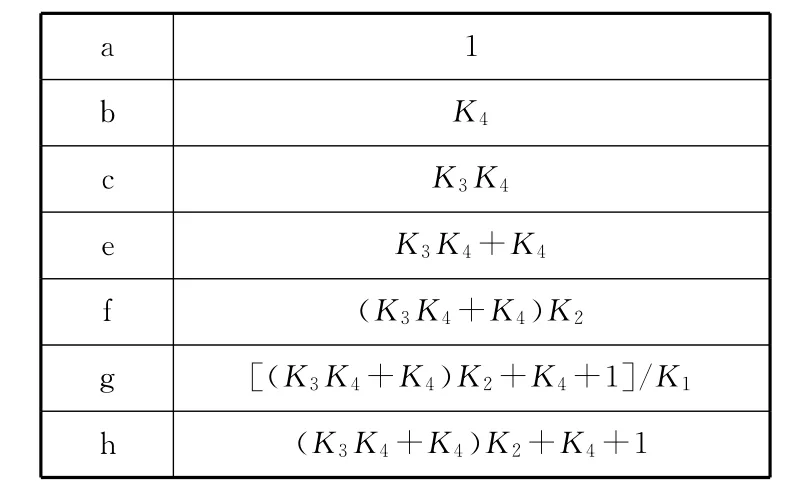
表2 用K值表示的各段长度

3 行星变速器力矩分析

杠杆法将变速器力矩分析简化为按平行力系平衡原理求解未知力的问题，使变速器的力矩分析变得形象直观.

（1）变速器行星机构外力矩

由力平衡原理可知：Mi＋MO＋MB＝0；且MO＝－iMi，可得 MB＝（i－1）Mi

由此得出5档时，输出力矩和制动力矩分别为：

（2）行星排内力矩

行星排内力矩是指各行星排的行星轮对该排的太阳轮，齿圈和行星架的作用力矩.可从外力矩已知并只受一个内力矩（即只参加一个行星排工作，不参与其他行星排工作）的构件出发.因该构件上的内力矩与此构件上的外力矩（已知）大小相等方向相反，故可求得该构件的内力矩.由行星排1可知：

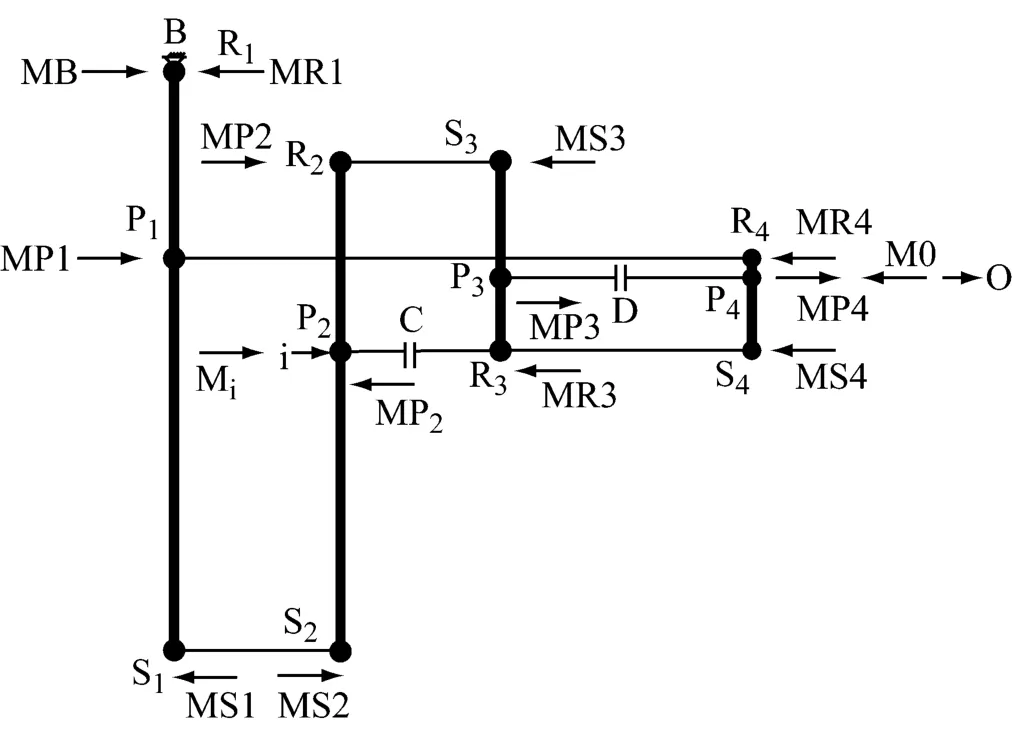
图6 等效杠杆法力矩分析Fig.6 Analysis of equivalent moment

齿圈所受的内力矩：MR1＝－MB＝－AMi；由杠杆的力平衡可求得太阳轮所受的内力矩：MS1＝－AMi/K1；

行星架的内力矩：MP1＝A（1＋K1）Mi/K1.如图6所示，S1和S2连接，可得太阳轮S2所受的内力矩：MS2＝－MS1＝AMi/K1；

由杠杆的力平衡可求得齿圈R2所受的内力矩：MR2＝AK2Mi/K1

行星架P2的内力矩：MP2＝－A（1＋K2）MI/K1.

S3和R2连接，可得太阳轮S3所受的内力矩：MS3＝－MR2＝－AK2Mi/K1；

由杠杆的力平衡可求得齿圈R3所受的内力矩：MR3＝－AK2K3Mi/K1

行星架P3的内力矩：MP3＝AK2（1＋K3）Mi/K1.P1和R4连接，可得齿圈R4所受的内力矩：MR4＝－MP1＝－A（1＋K1）Mi/K1；

由杠杆的力平衡可求得太阳轮S4所受的内力矩：MS4＝－A（1＋K1）Mi/（K1k4）；

行星架P4的内力矩：MP4＝A（1＋K1）（1＋K4）Mi/（K1K4）

其余档位也可以按此方法进行力矩分析.

（3）结合元件的接合力矩

① 一个结合元件只与一个构件连接，而不与其余构件连接

当某个构件作为制动点或作为输入点时，需要通过制动器或离合器来实现连接.其结合元件的接合力矩就等于输入力矩或制动力矩.

例如：5档时制动器B的接合力矩等于制动力矩Mb＝MB＝AMi.

②一个构件通过结合元件和另一个或多个构件连接

当两个构件通过结合元件连接时，两构件通过结合元件，使其具有相同的转速，结合元件两侧承受的力矩等值反向.而且与结合元件连接的构件力矩平衡，对构件进行力矩分析，可求出结合元件对该构件的力矩.

例如：5档时，构件P2、R3通过离合器C连接成一个整体，对构件P2进行力矩分析：

P2所受到的力矩有：输入力矩Mi；第二行星排行星轮对P2的力矩MP2；离合器C对P2的力矩Mc－p2。由三力矩平衡，可得离合器C对P2的接合力矩：Mc－p2＝－MP2－Mi＝［A（1＋K2）－K1］Mi/K1；离合器左侧承受的力矩：M C左＝－Mc－p2＝［K1－A（1＋K2）］Mi/K1；同理可得离合器C 右侧承受的力矩：MC右＝［A（1＋K2）－K1］Mi/K1.故离合器的接合力矩大小为MC＝｜MC左｜＝｜MC右｜.

由上述可求得离合器D的接合力矩：Md＝｜Md左｜＝｜Md右｜＝AK2（1＋K3）Mi/K1；

同理，可得各档位结合元件的接合力矩.

4 行星变速器效率分析

齿轮传动机构没有转速损失，其功率损失体现在力矩损失上，因此我们可以通过力矩来求效率.

效率为实际力传动比和理论力传动比（即机构μc为行星架固定时，从太阳轮至齿圈或从齿圈至太阳轮的传动效率（对单行星，可取μc＝0.97，对双行星，可取μc＝0.95）.

其余各档位效率可以按照该方法求得.传动比）之比，也即是实际输出力矩和理论输出力矩之比：

式中：机构传动比i＝f（K1，K2，…，Kl，…Kn）

式中各xl的正负可如下判断：

上式表示：

当为正时，xl＝＋1；当为负时，xl＝－1.

以5档为例，其速比为：

5 各档速比计算公式和效率汇总

其中：K1＝2.700，K2＝2.000，K3＝1.606，K4＝3.700

表3 各档速比、效率及其计算公式

6 结束语

利用杠杆法进行行星式变速器转速、转矩和效率分析，概念明确、直观和简单.能清楚地理解变速器设计者的意图.因篇幅所限，这里仅仅作简单介绍.应该说明杠杆分析法是应用面很广的普遍通用方法，适用于任何行星机构，不仅可用于行星机构解析；更适合用于行星机构设计，特别是用于开发出新型行星传动机构（变速器）的创新性的设计.因此我们认为很有必要在行业中推广应用此方法.

［1］ 黄宗益.现代轿车自动变速器原理和设计［M］.2006年9月.同济大学出版社.

［2］ 李 庆，黄宗益，李兴华.杠杆法在行星传动方案分析中的应用［J］.1999年10月同济大学学报.

［3］ 黄宗益，李兴华.轿车自动变速器杠杆分析法［J］.2002年第3期 传动技术.