调用不完全伽玛函数实现汽车传动轴强度的概率可靠性调优计算

张枫念

1 汽车传动轴的轴管

汽车传动轴是用在不同轴心的两轴间，甚至在工作过程中相对位置不断变化的两轴间传递动力。常见的汽车传动轴如图1所示。

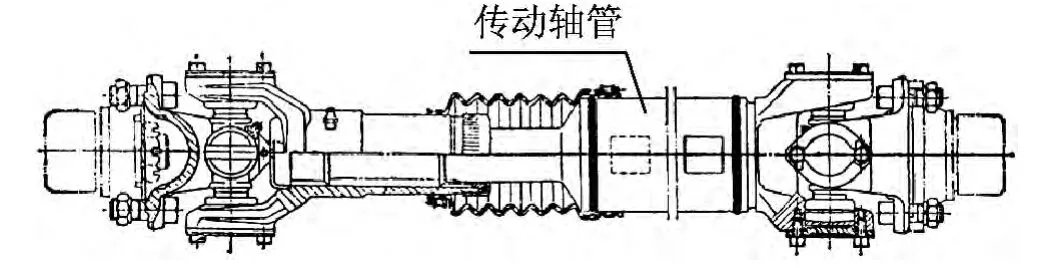
图1 汽车传动轴Fig.1 Drive shaft

在以往进行可靠性设计计算时，在计算得出可靠性系数后，还再要查表，才能得出可靠度值。因为直接计算时，其中的拉普拉斯函数是很麻烦的，为了手算方便，列出标准正态分布数值表供使用是很必要的，这样可减少许多计算工作量。然而这种做法在用计算机进行可靠性调优计算时是很不利的。因为它会阻碍计算机的自动高效的计算。现在我们通过编程，在计算机上采取调用不完全伽玛函数来实现传动轴可靠性调优计算。

传动轴管是采用钢板卷制再焊接而成的。采用不同厚度的钢板就能卷制出相同内径，不同的外径和管壁厚的轴管。这样在强度计算时可以只用变动管壁厚一个参数，即可计算出不同的强度。所以用它做例子来说明调用不完全伽玛函数实现传动轴可靠性的调优计算就比较容易理解。

汽车传动轴管一般由低碳钢板卷制的电焊钢管制成。壁厚比较均匀，一般壁厚仅为1.5～3.0mm，而管径相对较大，这是为了便于进行质量平衡，适用于高速旋转，管径相对较大，还能提高抗扭强度和弯曲刚度。传动轴上所受弯矩很小，可以忽略不计，而抗扭强度的安全系数是必须校核的。此外概率可靠性计算、疲劳强度的概率可靠性计算，也是经常验算的项目。也可用不完全伽玛函数对服从正态分布的概率可靠性进行调优计算，现对这些计算叙述于下。

2 传动轴抗扭强度安全系数的校核计算

已知某商用车传动轴所受的载荷、传动轴管的截面尺寸，现对其抗扭强度的安全系数作校核计算：如若传动轴管焊接管的钢板厚度δ＝0.0021～0.0025m范围内，传动轴管内径d2＝0.078m，传动轴管外径d1＝d2＋2δ，传动轴内外径比ae＝d2/d1，传动轴抗扭截面系数 wτ＝（1/16）×（π×d13）×（1－ae4），在发动机最大扭矩下传动轴的扭矩为Me时，传动轴管横截面上所承受的最大切应力可由下式算得：

τy＝ （Me/wτ）×10－6MPa

当发动机最大扭矩时传动轴上的扭矩Me＝1567.7 Nm，焊接钢管材料的许用切应力τx＝77MPa，传动轴抗扭强度的安全系数n＝τx/τy。以上校核计算的结果见表1所示。

3 服从正态分布的传动轴抗扭强度概率可靠性计算

若对上例进行概率可靠性计算则：因材料的许用切应力，与传动轴所受切应力，均为相互独立的随机变量。对机械耗损类失效概率一般都认是为服从正态分布，其变异系数不大时，也近似正态分布，其可靠性系数可采用联结方程求得：设发动机最大扭矩时传动轴管横截面上的切应力的均值为μτy，切应力的变异系数cστy＝0.03，切应力的标准差στy＝cστy×μτy，传动轴焊接管材料的许用切应力的均值为μτx，材料的许用切应力的变异系数cστx＝0.03，接管材料的许用切应力的标准差.στx＝cστx×μτx，安全系数n＝στx/στy ，

传动轴管可靠性系数u＝μy/σy，

例如传动轴管壁厚δ＝0.0023m可靠性系数u＝2.522954查表（即由可靠性系数查定可靠度表）且用插值法得可靠度R＝0.99413＋（0.9943－0.99413）×（2954/10000）＝0.9941802。

正态分布随机量标准差

4 用不完全伽玛函数实现传动轴抗扭强度的概率可靠性调优计算

从传动轴抗扭强度概率可靠性计算中知，要求在上述传动轴管壁厚δ范围内。计算它们各自的可靠度。并按照预先确定的可靠度R的要求即0.98≤R≤0.999，作为调优计算的选取目标。计算是在VB算法程序平台上，由所编制的专用程序来实现的，在运行中能进行无级的自动调优计算，从以下这些计算公式建立起的程序，即可知程序是具有不用查表就能算出可靠度的功能。

（1）调用不完全伽玛函数直接计算可靠度

采取调用一系列函数算法计算可靠度R。因为计算随机变量x的正态分布函数P（a，σ，x）值。正态分布函数的定义为；

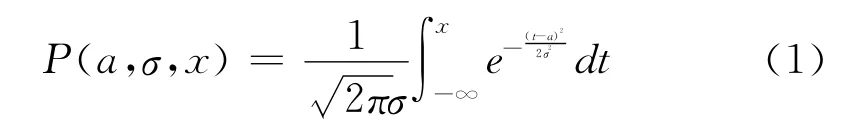
其中a为随机变量的数学期望（平均值）σ＞0，σ2为随机变量的方差。正态分布函数可以用误差函数来计算，即

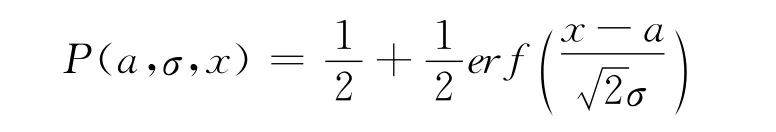
该函数返回一个实型函数值P（a，σ，x）.

该函数要调用误差函数，误差函数又要调用不完全伽玛函数。a实型变量，数学期望值，正态分布随机量均值；σ实型变量，σ2为方差值，σ＞0正态分布随机量标准差；x为—实型变量，随机变量值，为可靠性系数。

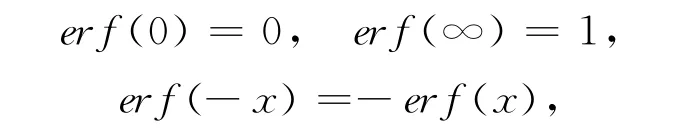
当x≥0时，可以用不完全伽玛函数计算误差函数，即

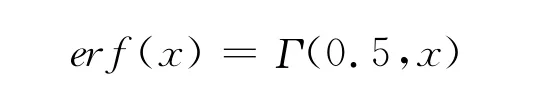
利用误差函数可以计算余误差函数

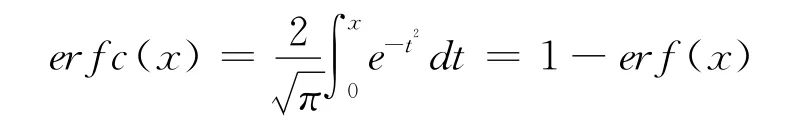
也可以计算正态概率积分

该函数返回一个实型的误差函数值。

该函数要调用不完全伽玛函数，

不完全伽玛函数定义为

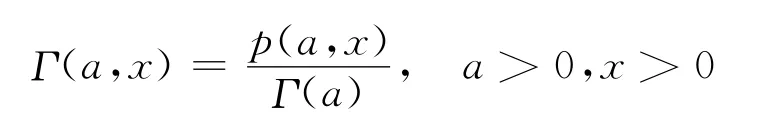
其中

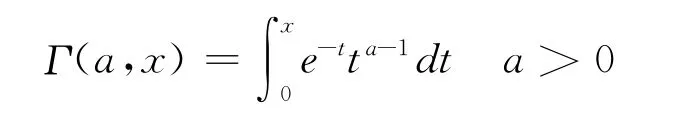
对于不完全伽玛函数有

Γ（a，x）＝0，Γ（a，∞）＝1

不完全伽玛函数也可表示为

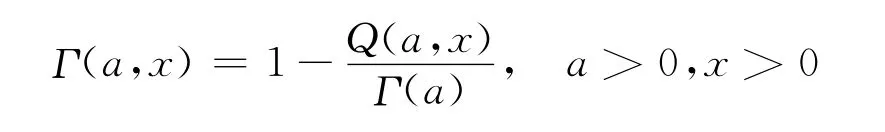
该函数返回一个实型的不完全伽玛函数值。

该函数要调用计算伽玛函数值的函数，采取调用一系列函数算法计算可靠度的最大好处是使程序在运行中成为一个完整的整体。如查表法，程序必须由于人机对话而断开。程序成为一个完整的整体它就能使参数在程序中实现自动调优。

（2）调优程序能很快计算出一组结果：如管壁厚度δ＝0.0021～0.0025m范围内，的可靠度，从以下一组可靠度值中可按优化的目标进行选取，这就被称为调优计算。

轴管壁厚δ＝.0021，调优所得可靠度Ru＝.6253688

轴管壁厚δ＝.0022，调优所得可靠度Ru＝.9260645

轴管壁厚δ＝.0023，调优所得可靠度Ru＝.9941679

轴管壁厚δ＝.0024，调优所得可靠度Ru＝.999805

轴管壁厚δ＝.0025，调优所得可靠度Ru＝.999997

由用不完全伽玛函数可直接调优计算的可靠度Ru与查表法所得的可靠度Rb作对比检验，所得的相对误差Δu见表1。

由于其最大相对误差Δu≤1.5%，即认为该调优软件可用，最后的计算书，可以将Ru、Rb同时列出。

若对子程序初始条件作适当的修正，可减少误差Δu，如若不进行修正，往往在计算的全程范围内，有部分的结果的相对误差将会≥1.5%。

由上述调优数据汇集可知，管壁厚度δ＝0.0023m的可靠度R，符合要求。该软件系统在调优计算的全程范围内，其最大相对误差Δu≤1.5%，认为合格可用。

5 传动轴疲劳强度的概率可靠性计算

以上是以传动轴最大切应力来进行概率可靠性计算，因传动轴也是经常承受着往复疲劳载荷，在实际损坏中也出现过疲劳损坏。在汽车传动轴台架试验方法及技术条件Q/T523标准中也要求做疲劳试验，它要求的工作循环数nxh＝1.5×105次工作循环，汽车传动轴不得出现任何损伤。以上面的参数为例，则可用以下方法进行计算：

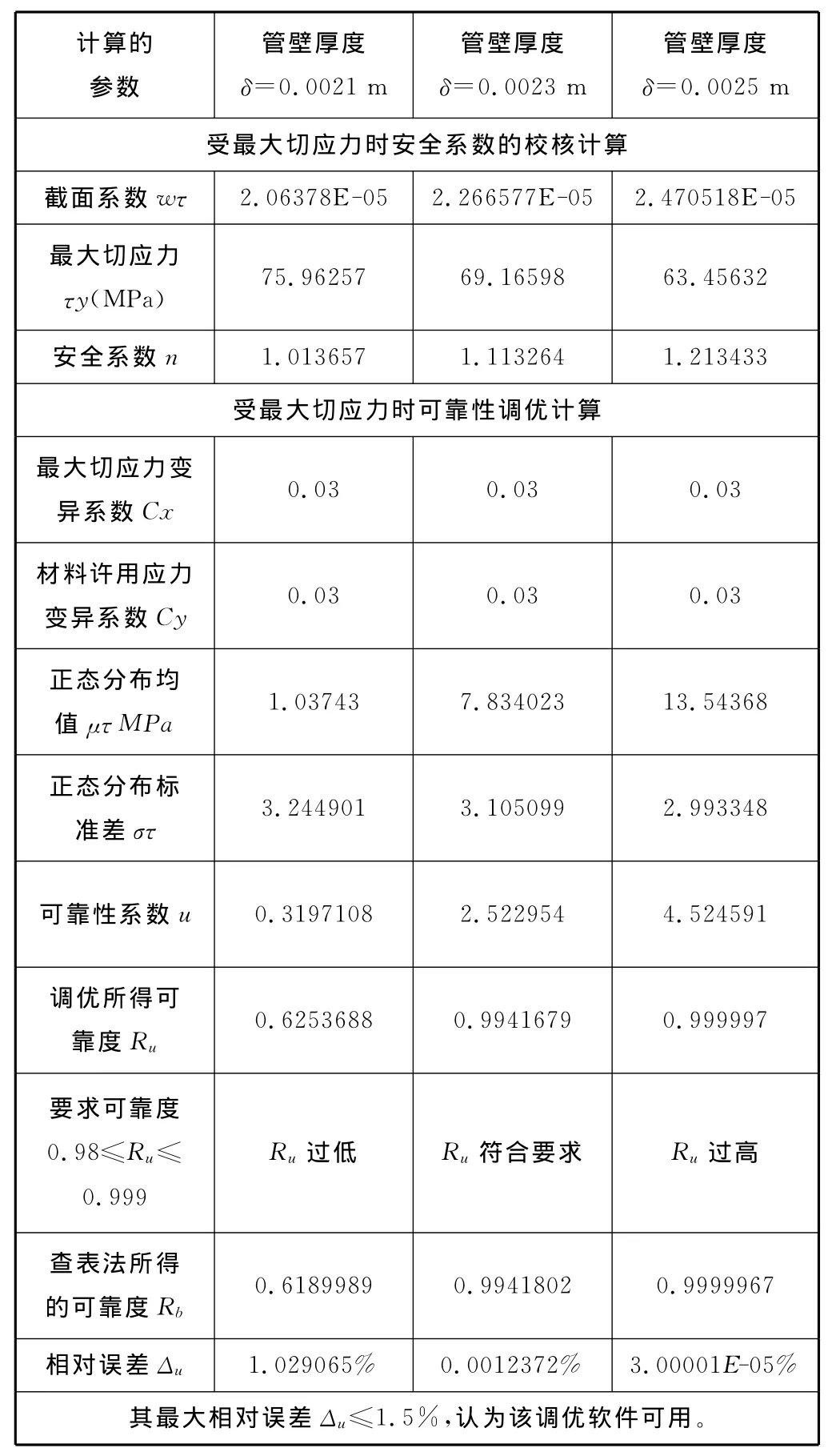
表1 传动轴强度安全系数校核及可靠性调优计算结果

已知传动轴管焊接管的钢板厚度δ＝0.0021、0.0023、0.0025m

传动轴内径d2＝0.078（m），其外径d1＝d2＋2δ，发动机最大扭矩时传动轴扭矩m，传动轴内外径比ae＝d2/d1，传动轴抗扭截面系数 w＝（1/16）×πd13×（1－ae4）疲劳试验工作循环数nxh＝1.5×105次循环，发动机最大扭矩时传动轴横截面所受切应力的均值μτy＝（m/w）×10－6（MPa）疲劳循环平均载荷导致的切应力均值μτm＝0.5×μτy（MPa），切应力的变异系数cστm＝0.04，所受切应力的标准差στm＝cστm×μτm，焊接钢管材料许用切应力的均值μτx＝77（MPa），焊接钢管材料许用切应力的疲劳极限均值假设为μτ－1＝0.8×μτx（MPa），焊接钢管材料许用切应力的变异系数cστ－1＝0.085材料许用切应力的标准差στ－1＝cστ－1×μτ－1。

因为疲劳失效概率可靠性的随机量分布服从对数正态分布；应力随机量均值μ＝μτ－1－μτm，标准差随机量，服从对数正态分布可靠性系数z＝（ln（nxh）－μ）/σ，若选管壁厚度δ＝0.0023m则z＝－1.545958查表后且用插值法得标准正态分布值φz＝0.06178＋（0.06178－0.06057）＊（5958/10000）＝0.006832147，而可靠度R＝1－φz＝0.993167853。

在上一节用不完全伽玛函数实现传动轴抗扭强度的概率可靠性调优计算，这是对服从正态分布可靠度计算为前提的，在此前提下是有效的，因为其计算程序是建立在正态分布函数子程序上的，而在计算疲劳强度的概率可靠性时，由于疲劳失效概率可靠性的随机量分布是服从对数正态分布的。

对于服从对数正态分布可靠度的计算，则在算法中的有关公式将有所不同如程序中原来的式（1）处，应选择式（2）

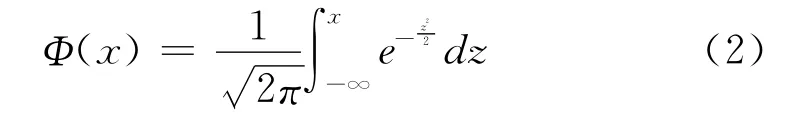
以式2来建立调优计算的程序。对服从对数正态分布的疲劳强度概率可靠度Rz进行计算，与查表法所得的可靠度Rb作对比检验，所得的计算结果及相对误差Δz见表2。

该软件在调优计算的范围内，其最大相对误差Δz≤1.5%，认为该调优软件可用，最后的计算书，可将Rz、Rb同时列出。

若对子程序初始条件作适当的修正，可减少误差Δz，如若不进行修正，往往在计算的全程范围内，有部分的结果的相对误差将会≥1.5%。

由上述调优数据汇集可知，管壁厚度δ＝0.0023m的可靠度Rz，符合疲劳可靠度要求。该软件系统在调优计算的全程范围内，其最大相对误差Δz≤1.5%，认为合格可用。

以上仅借用汽车传动轴强度的概率可靠性计算来说明调用不完全伽玛函数，实现汽车传动轴强度概率可靠性的调优计算。

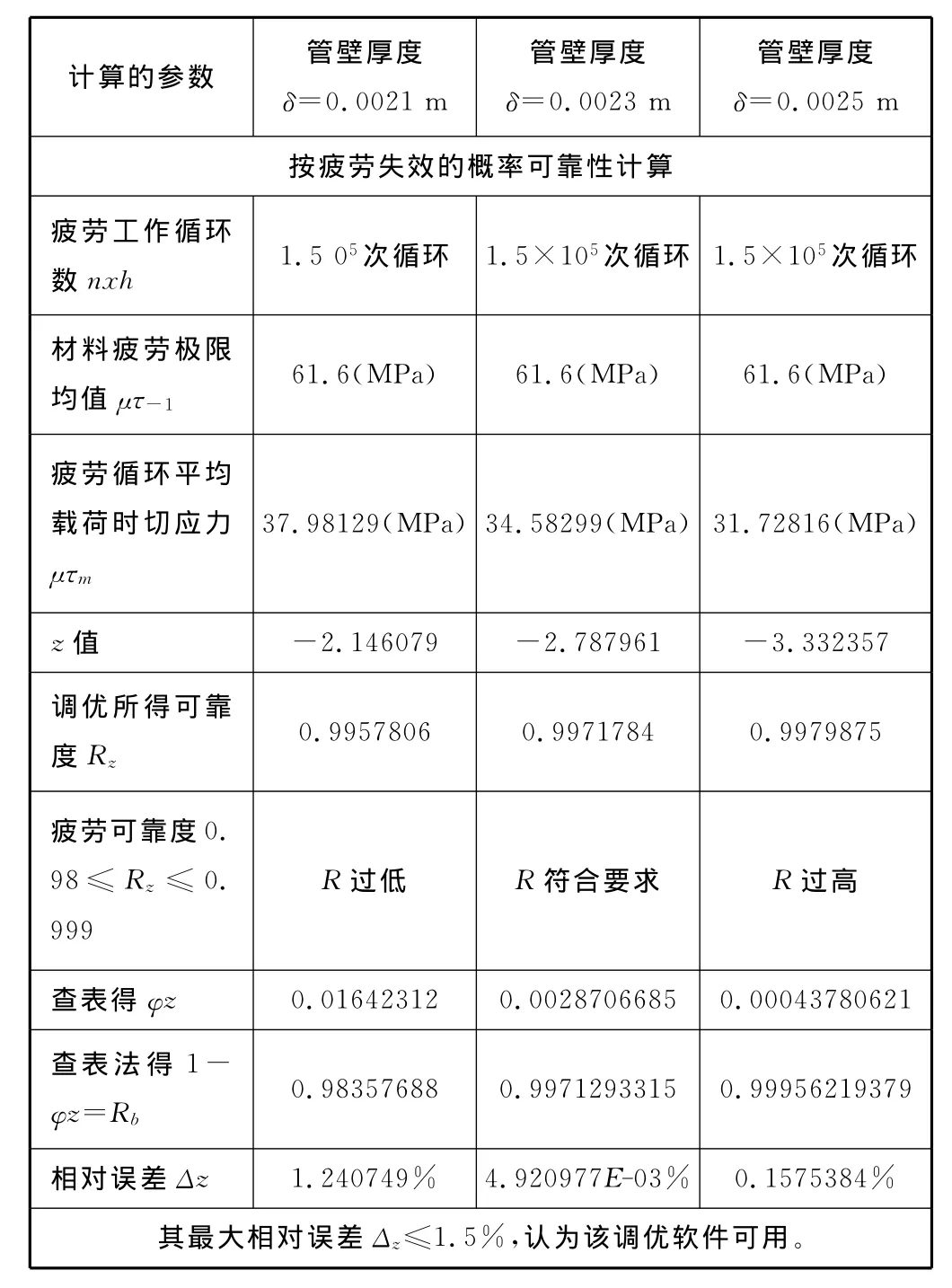
表2 传动轴疲劳失效概率可靠性的计算结果

籍此与业界探讨交流一种简便、实用的概率可靠性的调优方法。

［1］ 徐士良编著QBASIC常用算法程序集.北京：清华大学出版社1997

［2］ 何光渝编著Visual Basic常用算法程序集.北京：科学出版社2002

［3］ 张小虞 汽车工程手册 北京：认民交通出版社2000

［4］ 芮延年 现代可靠性设计.北京：国防工业出版社2007

［5］ 刘怀金 传动轴在整车中的布置设计 南京 轻型汽车技术2013.11/12

［6］ 张枫念 机械可靠性设计与VB编程实例 北京 化工出版社2010

［7］ 张枫念 实用机械设计VB编程及实例（第二版）.北京：化工出版社2012