2.5MW风电齿轮的设计及工艺研究

陈宗瑞 吴 刚

（南车戚墅堰机车车辆工艺研究所有限公司 江苏 常州 213011）

1 前言

随着国内风电技术的不断发展1.5MW级别的风机已经逐渐退出市场，2.5MW级别的风机将成为国内市场的主流机型。风电齿轮作为风电齿轮箱中的核心部件，对其承载能力和可靠性提出了更高的要求。我国大型风电齿轮箱的发展才刚刚起步，还缺乏系统深入的设计研究和对核心设计手段的掌握。在2.5MW风电齿轮箱的设计过程中，我们充分发挥了我公司在齿轮设计、新材料、新工艺及新技术等方面的综合优势，将设计、材料、热处理、锻造、制造等方面作为一个系统进行分析研究，寻找合理的齿轮设计方法来满足风电齿轮传动系统的设计要求和使用要求。

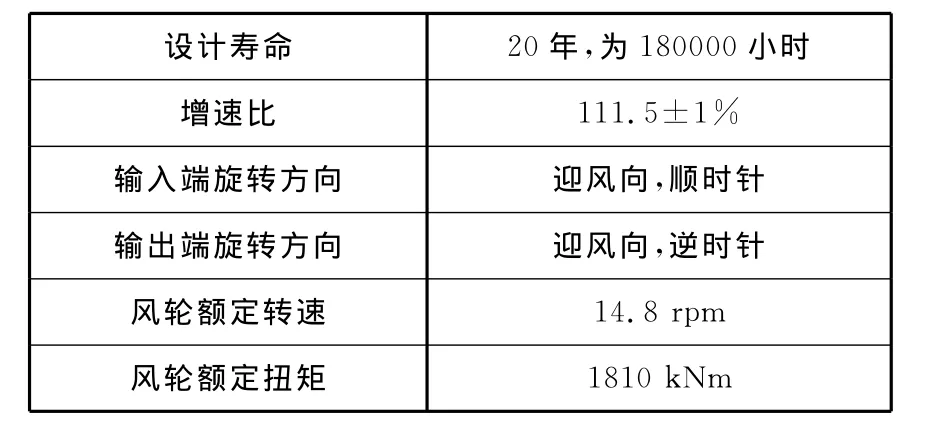
表1 2.5MW风电齿轮箱技术参数

2 设计输入

3 概念设计

2.5MW风电齿轮传动系统采用两级行星轮系加一级平行轴传动（如图1）。两级行星轮均采用NGW型，齿圈固定，行星架输入，太阳轮输出。为提高承载能力和啮合平稳性各级齿轮均采用斜齿轮设计，为将齿轮啮合产生的轴向力传递到下风向太阳轮的旋向采用左旋，行星轮和内齿圈为右旋。外齿轮设计精度ISO1328 5级，内齿圈设计精度为ISO1328 6级。材料性能和热处理需满足ISO6336－5中MQ级要求。

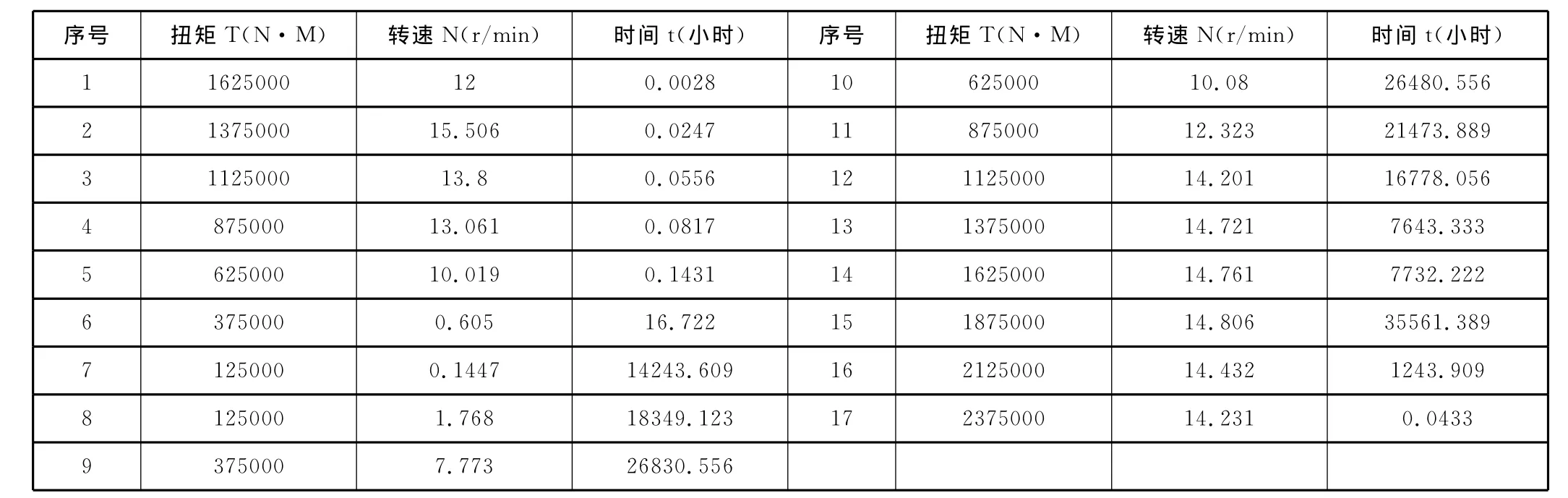
表2 2.5MW风电齿轮箱输入扭矩时间分布序列（LDD）

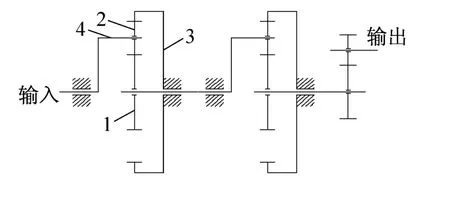
图1 两级NGW行星轮系加一级平行轴传动系统Fig.1 Transmission schematic

4 齿轮参数的详细设计

齿轮的主要啮合参数有模数、齿数、压力角、螺旋角、变位系数等。这些参数在中心距和传动比确定后，相互影响、相互制约，必须根据不同的使用场合和要求反复计算和多方案比较，根据各个啮合参数对齿轮传动质量和可靠性的影响，以及考虑所设计齿轮最有可能产生的失效形式，选取一组最佳的齿轮啮合参数。图2为Planetary＿NGW设计系统的操作界面，系统提供了概念设计、几何计算、变位系数选择、强度分析、载荷谱计算等模块。

图2 Planetary＿NGW设计系统操作界面Fig.2 The interface of Planetary＿NGW

（一）传动比分配

针对两级行星齿轮加一级平行轴（下面简称高速级）结构的风电齿轮箱，首先确定高速级的传动比，根据我们的设计经验高速级的传动比要求不能大于5。此外考虑到在配齿计算的过程中各级传动比会出现微调，所以我们在初分传动比的时候将高速级的传动比选在4左右。然后两级行星轮的传动比按各级之间等强度和获得经济的外廓尺寸为原则进行分配。最终得到各级传动比的初始值为：i1＝5，i2＝5.6，i3＝4。

（二）行星轮个数的选择

行星齿轮的个数将影响行星机构的均载性。提高行星传动均载性可以均衡各行星轮传递的载荷，补偿制造误差，提高齿轮的承载能力、啮合平稳性和可靠性，同时降低对齿轮的精度要求。GL中也提到：对于3个行星齿轮均载系数kHP＝1，4个行星齿轮均载系数kHP＝1.25，5个行星齿轮均载系数kHP＝1.35。因此，在选择行星轮个数的时考虑到行星齿轮的均载性和经济性我们首选np＝3，其次选np＝5。

（三）模数的选择

对于风电齿轮，在选取模数时必须首先保证齿轮轮齿具有足够高的齿根强度。见公式（1）：

公式（1）中：

Ktm为计算系数；

KFΣ为综合系数；

YFα1为小齿轮齿形系数；

σFlim为试验齿轮弯曲疲劳极限。

（四）配齿条件

在NGW行星传动机构配齿设计过程中，齿轮的齿数及行星轮个数必须满足邻接条件、同心条件、装配条件等三个基本约束条件。

1.同心条件：保证太阳轮、内齿圈与行星架轴线重合的条件下的正确啮合，由各对啮合齿轮间的中心距必须相等。见公式（2）：

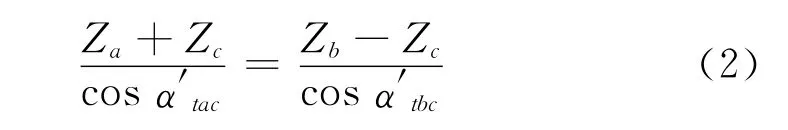
2.装配条件：保证各行星轮能均布地安装于内齿圈和太阳轮之间。为此，太阳轮、内齿圈的齿数与行星轮的个数必须满足装配条件，否则，当第一个行星轮装入啮合位置后，其他几个行星轮装不进去。见公式（3）：

3.邻接条件：保证相临两个行星轮的齿顶不相碰。见公式（4）：

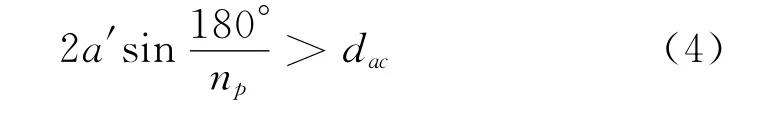
此外，为了减少振动噪声和提高工作平稳，各啮合齿轮的齿数之间应没有公约数，同时太阳轮和内齿圈的齿数不宜为行星轮个数的整数倍。对于高速级大齿轮尽量不选用大于100的质数（如101，103，…），因为加工大于100的质数齿轮时调整机床的挂轮比较困难。在实际的方案设计中还要了解改变齿数对轮齿强度及啮合质量等传动特性的影响。如果齿轮的承载能力主要取决于齿面接触疲劳强度，则选择较多齿数和较小模数方案是合理的。反之，如果齿轮承载能力取决于齿根弯曲强度，则选择较少齿数和较大模数方案是合理的。

（五）变位系数的选择

选择合理的变位系数可在不增加成本的基础上，最大限度地提高齿轮承载能力，如：齿轮的抗胶合性、齿根弯曲强度、齿面接触强度等。所以，在设计中为了提高齿轮传动的承载能力，外齿轮我们多采用正角变位，内齿轮我们多采用负角变位。此外，在设计中一般控制总变位系数Σx小于1.2。在Planetary＿NGW软件（如图3）中提供了4种变位系数分配方法：等滑动法、等弯曲B法、等弯曲C法、改变节点位置法，在实际应用中，可以根据不同的设计需求选择不同的变位系数分配方法。同时变位系数的选择还必须满足一定的限制条件：无根切限制条件、齿顶齿厚限制条件、重合度限制条件，图4为Planetary＿NGW软件中得出的变位系数限制条件曲线，无侧隙啮合曲线和等滑动曲线交点必须同时满足在“重合度＝1.2”曲线下方，以及在“Sa＞0.4 mn”曲线和“无根切”曲线上方的限制条件。

在风电齿轮的设计中，行星轮系的变位系数分配多采用等滑动原则，即通过变位系数的选择使太阳轮和行星轮的齿根处的滑动率相等。但在变位量较大时，节点会明显偏于啮合线的一侧。对于存在胶合危险的齿轮，应当采用改变节点位置法使得啮合线上的啮出段和啮入段差不多一样长，但考虑到齿轮在啮合过程中存在弹性变形总是提前啮入和延迟啮出，所以在实际设计中啮入长度要稍小于啮出长度。因为齿轮在啮入端工作时，轮齿总是挤进运动，边挤边刮，容易磨坏齿面；在啮出端工作时，轮齿之间总是滑出运动，齿面之间具有抛光和冷作硬化作用，可以提高齿面的疲劳强度，这对轮齿工作有利，摩擦也较小。

（六）其他啮合参数的选择

选择压力角时，大压力角有利于齿轮的强度（接触、弯曲和胶合），而小压力角有利于齿轮的动态特性（如噪声和振动）。对于低速级齿轮由于其动载荷大，在满足重合度等动态特性参数要求的条件下，可以采用大压力角来提高其承载能力。对于高速级齿轮由于其转速高，需要一个强度和动态特性的折中值，故高速级齿轮多采用20°压力角。

图3 变位系数分配计算Fig.3 Calculation of the modification coefficient distribution

图4 变位系数限制条件曲线Fig.4 The modification coefficient limits curve

选择螺旋角时，增大螺旋角可以提高轮齿的承载能力，提高工作的平稳性和降低噪声。但增大螺旋角后，轴承所受的轴向力将增大，同时使轴易发生倾斜，齿面的温升将增加，对齿面胶合不利。综上所述，对于第一级行星轮系转速低，轮齿啮合频率也低，噪声不大；但扭矩很大，如果采用大螺旋角，轴承上承受的轴向力就很大，轴承的选择很难足设计要求，所以第一级螺旋角一般采用6°～8°为宜。为了内齿圈的制造方便，第二级通常选择与第一级同样的螺旋角。对于高速级振动较大，而扭矩较小，通常采用12°～15°螺旋角。

（七）传动质量指标的验算

啮合参数初步确定之后，需要验算重合度、滑动率、几何压力系数和机械效率四大传动质量指标。一般情况下，要求重合度ε大于1.2，滑动系数η小于1.5，比压系数ξ小于1.4，机械效率大于98%。图5为使用Planetary＿NGW软件对传动质量指标进行验算。

（八）变载荷下齿轮强度的计算

对于变载荷下的齿轮强度计算，我们先利用Palmgren－Miner定则将载荷谱等效成为当量扭矩Teq，见公式（5）、（6）。再以此当量扭矩Teq代替名义扭矩T来校核齿轮的疲劳强度。图6为使用Planetary＿NGW对载荷谱进行处理后输出的结果。

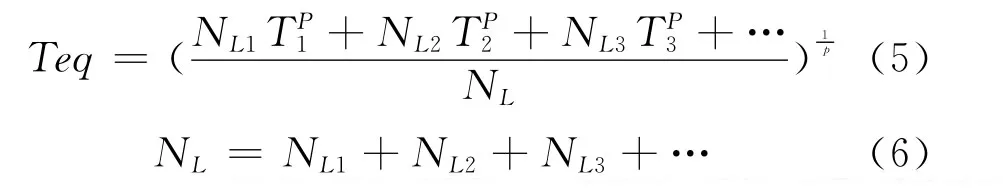
公式（4）中：p为材料的试验指数。

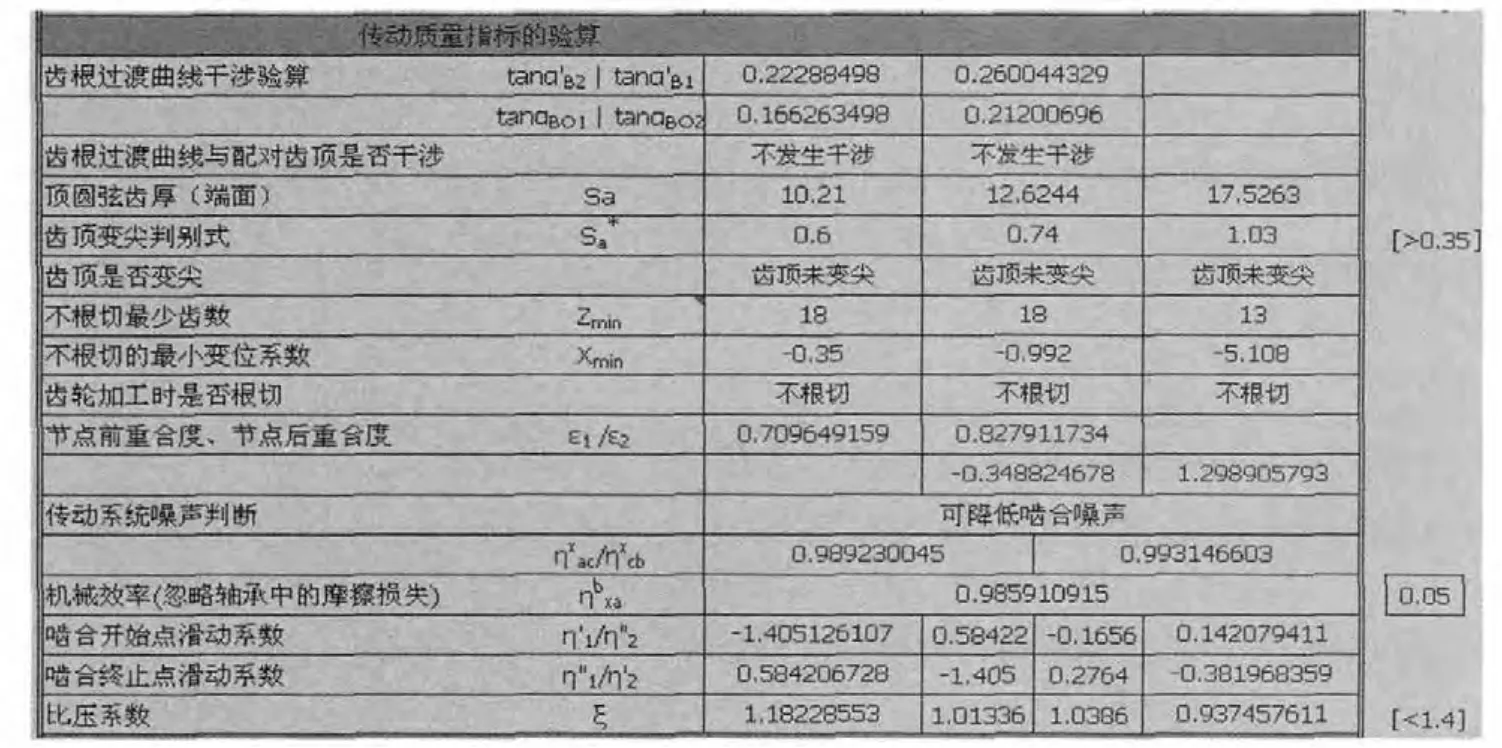
图5 传动质量指标验算Fig.5 Checking the transmission quality

图6 载荷谱处理计算Fig.6 Load spectrum calculation

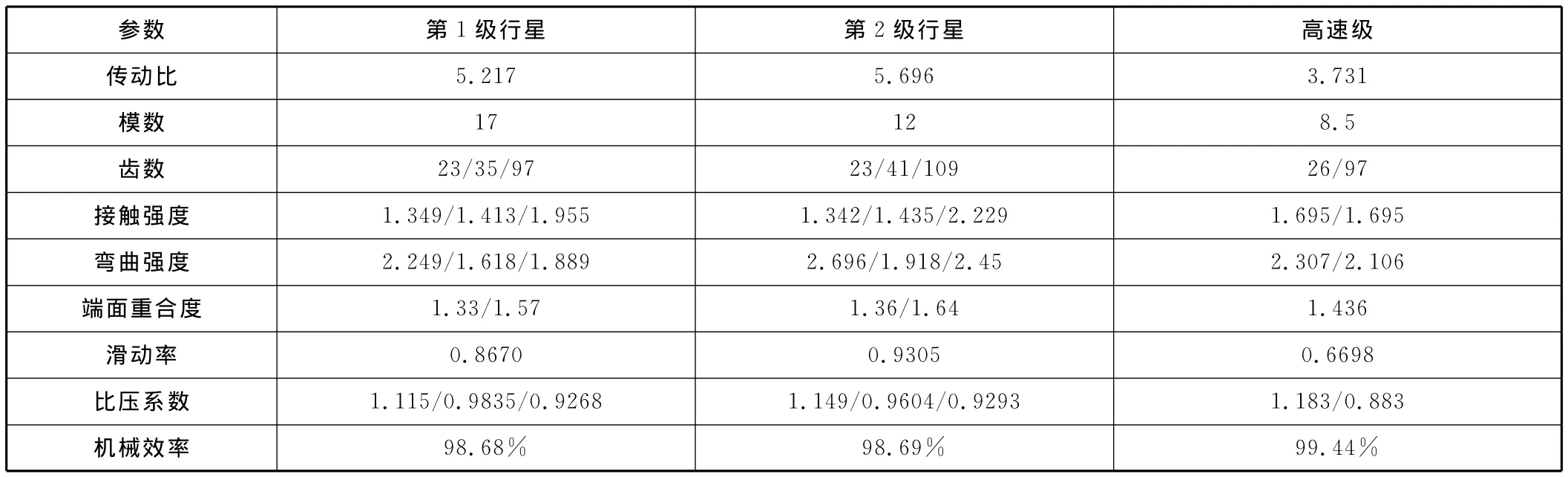
表3 风电齿轮参数表

同时，在计算过程中要求均载系数kHP取1.0，动载系数Kv不小于1.05，齿向载荷分配系数kHβ不小于1.15，接触安全系数SH要求不小于1.2，弯曲安全系数SF要求不小于1.5。根据我们公司现有的热处理工艺水平，外齿轮接触疲劳极限取1 450 N/mm2、弯曲疲劳极限取450N/mm2，内齿轮接触疲劳极限取1 200N/mm2、弯曲疲劳极限取370N/mm2。齿面粗糙度Ra取0.8，齿根粗糙度Ra取3.2。基本齿条的齿根圆角半径取0.38 mn。

（九）最终方案的确定

经过反复的计算和多方案的比较，综合考虑风电齿轮最有可能产生的失效形式，最终选取了下面一组齿轮啮合参数，参数方案的安全系数和传动指标均满足设计要求。

5 齿形设计优化

齿廓修形和齿向修形是不改变齿轮的啮合几何尺寸，仅仅是改善啮合过程和啮合部位，来提高齿轮传动的可靠性和强度。正确的修形可以补偿制造误差、安装误差和弹性变形，也可以提高传动运行的平稳性，减少噪声和振动，所以在风电齿轮设计中我们也采用齿廓修形和齿向修形进行齿形设计优化。由于齿轮、轴、轴承、行星架和箱体都是柔性部件，上述部件在受力后会产生弹性变形导致齿轮啮合错位，在修形计算过程中必须充分考虑风电齿轮箱系统变形对齿轮啮合的影响。我们在Ro－max软件中建立风电齿轮箱系统级分析模型（如图7），并将Planetary＿NGW软件根据弹性力学理论计算出的修形结果（如图8）带入Romax软件中进行分析计算。

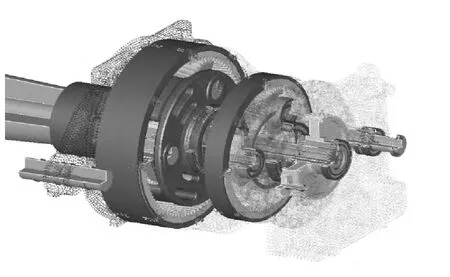
图7 系统及建模分析Fig.7 System modeling and analysis

图8 Planetary＿NGW中修形计算Fig.8 Gear modification calculation

在Romax软件中，应首先对行星轮进行齿廓修形和齿向修形。由于行星轮的两侧齿面分别参与内啮合和外啮合，我们对外啮合侧齿廓的采用齿顶修形，对内啮合侧齿廓采用齿顶和齿根修形，对行星轮两侧齿向采用修鼓、修边加螺旋角修形，螺旋角修形量的确定主要考虑抵消行星轮和内齿圈的啮合错位影响。对太阳轮两侧齿廓同时采用齿顶修形，太阳轮两侧齿向采用修鼓、修边加螺旋角修形。考虑齿轮加工的经济性，对内齿圈的齿廓不进行修形仅在节圆处减小齿形公差，要求磨齿时在公差范围内曲线圆滑过渡即可。

在Romax软件中反复调整微观修形参数和多方案的比较，直至两齿轮啮合产生的接触斑位于齿向中部为止，图9为行星轮与内齿圈啮合时产生的应力分布，图10为行星轮与太阳轮啮合时产生的应力分布。为了验证设计的正确性，我们在齿轮箱样机型式试验后将齿轮箱进行拆解，检查各齿面的实际啮合情况（如图11），确保齿轮达到最佳的工作状态。

图9 行星轮与内齿圈啮合应力分布Fig.9 Planetary gear and the ring gear stress distribution

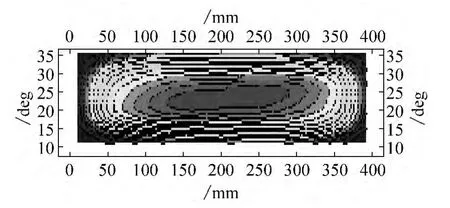
图10 行星轮与太阳轮啮合应力分布Fig.10 Planetary gear and the sun stress distribution

6 齿轮工艺的研究

（一）热处理工艺的优化

图11 行星轮实际啮合接触斑Fig.11 The planet wheel actual contact spot

材料的性能是齿轮承载能力的基础，合理选择材料和热处理工艺可以使齿轮在充分满足设计要求的同时，降低制造成本。风电齿轮在实际运行中多出现齿面疲劳点蚀，必须把提高齿轮抗疲劳点蚀能力作为选择齿轮材料和热处理工艺的一个重要性能指标。因此，外齿轮均采用18CrNiMo7－6（DIN 17210）低碳合金钢，采用渗碳淬火工艺。根据经验当齿面硬度低于57HRC时，齿面接触疲劳强度会显著下降，而当齿面硬度高于63HRC时，齿轮材料的脆性增加轮齿的弯曲疲劳强度将显著下降。国际著名齿轮专家温特提出了“当齿面硬度高于58HRC后，齿面硬度的提高对齿面接触强度的影响已不再明显。”，国内航空齿轮专家江甫炎认为“齿轮表面硬度的稍微下降并不影响耐磨性，而齿轮的综合机械性能反而得到提高。”，此外当硬度高于60HRC时，在磨削（磨内孔、端面和磨齿工序）加工过程中容易出现磨削烧伤，将严重影响齿轮的接触疲劳强度导致齿轮提前失效。故外齿轮的齿面硬度选择58～62HRC为最佳，芯部硬度一般控制在30～45HRC为宜。内齿圈采用42CrMo4（EN 10085）调质合金钢，采用调质加中频感应淬火工艺，齿面硬度为53～58HRC。

渗碳齿轮的抗疲劳点蚀能力与渗碳层的深度有很大关系。为避免点蚀剥落现象，渗碳层深度hc（磨齿之后的）至少应大于最大剪切深度的2倍，如图12为Planetary＿NGW软件中对有效硬化层深的计算结果。

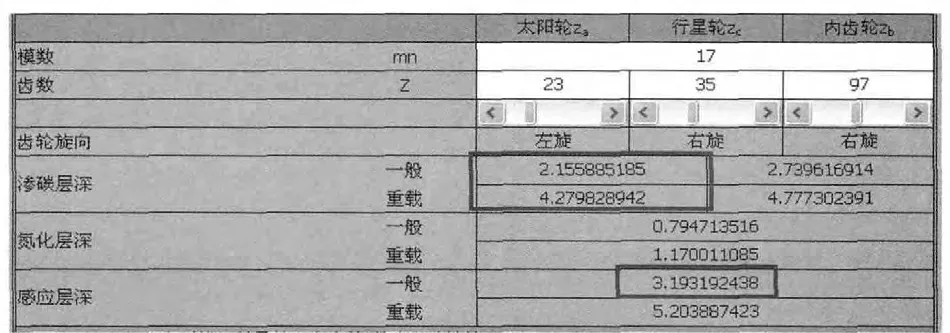
图12 Planetary＿NGW中有效硬化层深计算Fig.12 Effective hardened layer depth calculation

为了尽量减小热处理变形，以保证各齿面磨削余量一致，使各齿面最终获得一致的含碳量、金相组织和硬度，从而得到均匀的工作性能，外齿轮须在粗车和半精车之间增加一次预备热处理工序，消除组织的不均匀和内应力，改善切削性能，增强最终热处理的效果。为提高内齿圈的机械性能和轮齿强度，调质处理须放在粗铣齿和精铣齿两道工序中间；同时在感应淬火工序前增加去应力退火工序，消除加工过程中产生的残余应力，能够很好地避免淬火裂纹的产生。

（二）齿轮滚刀的选用

在产品制造阶段，为进一步提高齿轮抗弯曲疲劳强度，须选用专用的凸角留磨滚刀，它加工出的齿轮具有一定的根切量，对磨齿工艺来说起到了退刀槽的作用。在设计滚到刀时应尽量增大刀尖圆弧，以减小应力集中，增强齿根强度；同时滚刀设计必须保证刀具所加工出的齿轮具有足够的渐开线长度，即：渐开线起始点直径要小于最低啮合点直径。图13为滚刀模拟计算，凸台高度、凸台角度和凸台圆角半径是影响齿根圆弧及过渡曲线型线形状的关键参数：

1.凸台高度：凸台高度根据轮齿的单边磨削余量及附加挖人量确定，风电齿轮的磨削余量为0.4～0.5mm，凸台高度确定为0.45～0.55mm。

2.凸台圆角半径：设计时应尽量增大凸台圆角半径，将刀尖圆角圆心至刀齿对称线的距离E值越接近于零越好。

3.凸台角度：凸台角度过小会造成侧后角偏小，切削过程中滚刀容易磨损，但凸台角度过大时会使凸台圆角半径和凸台高度变小，设计时应综合考虑选取最佳值。

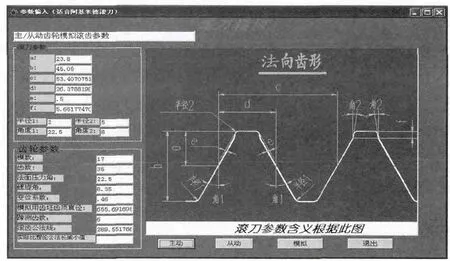
图13 滚刀模拟计算Fig.13 The simulation calculation of hob

根据滚刀的设计参数，在软件中对行星齿轮进行模拟滚齿加工（见图14）。由图13可见，在磨齿后齿轮的渐开线起始圆直径dc小于最低啮合圆直径dz，同时齿根过渡曲线处存在一定的沉割量。

图14 行星齿轮模拟加工图Fig.14 The simulation of planetary gear machining

7 结束语

为了保证2.5MW风电齿轮的安全性和可靠性，我们进行了大量的方案对比和试验验证，并将齿轮放在整个传动系统中进行设计和优化，使2.5 MW风电齿轮能够满足在相对恶劣环境下使用要求和寿命适应20年的设计寿命要求。

［1］ 陈宗瑞，吴刚，阙红波.1.65MW风电齿轮的设计及工艺研究［J］.机车车辆工艺，2011第1期：5－8.

［2］ 吴刚，陈宗瑞.机车牵引齿轮寿命预测方法探讨［J］.机车车辆工艺，2008第6期：7－8.

［3］ 吴刚.地铁牵引齿轮凸角留磨滚刀的设计［J］.机车车辆工艺，2005第8期：22－23.

［4］ 许洪基，陶燕光，雷光.齿轮手册第2版［M］.北京：机械工业出版社.2000.

［5］ G.尼曼.机械零件［M］.北京：机械工业出版社.1985.

［6］ 江甫炎.近代齿轮制造工艺［M］.北京：机械工业出版社.1994.