Ru掺杂MnO2电子结构的第一性原理浅析

罗 帆，王 欣，刘雪华，唐 电，

(1．福州大学材料科学与工程学院，福建福州 350116;2．福州大学材料研究所，福建福州 350116)

0 引言

二氧化锰具有储量丰富、价格低廉和对环境友好的特点，是重要的电化学工业电极材料［1］．二氧化锰最主要的用途之一是作为电池材料，并且已被大量应用于生产干电池．近十年来，作为新能源电极材料，包括超级电容器和锂电池等，二氧化锰也引起了人们极大的关注［2－4］．1999年，Lee等［5］将二氧化锰用作超级电容器材料，但是其比电容较低，电化学活性不高．为了提高二氧化锰电极材料的性能，研究人员采取向二氧化锰掺杂其他元素，如制备钛锰、钴锰、镍锰、钌锰和铱锰等复合氧化物电极材料［6－9］．其中，以钌锰和铱锰复合氧化物电极材料最受关注．这主要是因为二氧化钌和二氧化铱本身就具有非常优秀的电催化性和金属导电性，如将它们与二氧化锰混合制备成复合氧化物电极材料，不仅能明显提高电极的活性，还可以很好地控制电极材料的成本．文建国等［6］采用添加原子分数为10%的二氧化钌，制备出钌锰复合氧化物电极材料，比纯二氧化锰电极材料有更高的比电容和电化学可逆性．Chou等［10］制备的钌锰复合氧化物电极材料显示了良好的电化学稳定性以及高比电容．Kim等［11］采用软化学反应制备的钌锰复合氧化物电极材料能够很好地提高电导率，进而促进电容量的提升．刘志锋［12］采用湿化学法制备含有金红石型固溶体的钌锰复合氧化物电极材料，显示了其具有良好的电催化活性．当然，有关钌锰复合氧化物电极材料的报导都是实验研究，对于其活性提升的机理并未深入研究，也尚未见到钌锰复合氧化物电极的第一性原理的研究报导．鉴于采用第一性原理可以提供掺杂二氧化钌后材料的电子结构变化的特点，可以通过导电机理进而分析电极材料性能［13］，因此，拟引入基于密度泛函理论(DFT)的第一性原理方法，分析Ru掺杂金红石型 MnO2(β－MnO2)后形成 Mn0．875Ru0．125O2复合氧化物的晶体结构变化特点，对比Ru掺杂金红石型MnO2前后的能带以及态密度，进而分析钌锰复合氧化物电极材料的导电机理．

1 计算方法

采用基于密度泛函理论第一性原理方法的软件包Vienna ab－initio simulation package(VASP)［14］完成计算，详见文献［15－17］．价电子间的交换关联能采用广义梯度近似方法GGA［18］，价电子和离子间相互作用选用投影缀加平面波，系统的波函数通过平面波基组展开．经测试，本实验的平面波基函数的截断能参数设置为520 eV，并选用6×6×6个Monkhorst－Pack特殊点对布里渊区进行积分以获得更高精度的系统总能．采用周期性边界条件，并认为Ru在MnO2超胞中不同取代位置掺杂对计算结果无实质性的影响．体系总能量的收敛精度为每个原子总能变化小于2×10－5eV，原子间的作用力收敛标准小于0．5 eV·nm－1．

MnO2和RuO2均为金红石结构，空间群为P42/mnm，对称性D4h－14，属体心四方晶系．本实验的金红石型MnO2超胞由8个Mn原子和16个O原子构成，是在金红石型MnO2原胞的a、b基矢上分别扩展1个单位得到2×2×1个原晶胞大小的超胞，在金红石型MnO2超胞中，以Ru原子替换Mn原子，结构模型见图1．通过几何结构优化后，计算出掺杂前后的晶格常数，并利用三阶Birch Murnaghan［19］状态公式方程式对体系的体积和总能关系曲线进行E－V曲线的拟合，获得了平衡条件下的结构数据和总能．最后，计算掺杂前后的金红石型MnO2的能带结构和电子态密度，考虑的价电子有:O的2s2p态，Mn的3d4s3p态，Ru的4d5s4p态．

图1 计算结构模型Fig．1 Structure model for calculation

2 结果与讨论

2．1 晶体结构分析

图2表示金红石型MnO2和Ru掺杂金红石型MnO2的超胞体积与系统总能之间的关系．表1列出了经过三阶Birch Murnaghan拟合后的晶胞常数和相关文献的数值．尽管未查到采用密度泛函理论计算Mn0．875Ru0．125O2的数据，但为了证实数据的可靠性，将所计算的金红石型MnO2和RuO2数据与文献报道的数据进行比较．从表1可以看出，金红石型MnO2的晶胞常数a=b=0．445 nm，c=0．274 nm与Hu等［20］计算的晶胞常数基本吻合(a=b=0．445 nm，c=0．273 nm)．通过GGA的计算方法获得的金红石型MnO2的晶胞体积为0．054 nm3与标准卡片值(JCPDS24－0735 0．056 nm3)相对误差为－3．57%．Benyahia等［21］通过GGA方法计算得出的金红石型RuO2的晶胞体积为0．065 nm3，与标准卡片值(JCPDS 40－1290 0．063 nm3)相对误差为3．17%．Klug等［22］通过GGA方法计算得出的这一数值为0．065 nm3，相对误差为3．17%．本实验通过GGA的计算方法获得的金红石型RuO2的晶胞体积为0．064 nm3，与标准卡片数值0．063 nm3间的相对误差绝对值(1．59%)均小于以上两篇文献报导的数值，这说明此计算方法以及参数设置较为可靠．由表1还可以看出，金红石型MnO2掺杂少量Ru后，形成离子型固溶体［12］，晶胞常数a、c增大，晶胞体积也同样增大，相对而言，c值增大比例更高，说明Ru掺杂后出现一定程度畸变．这种现象的出现主要是由于Ru4+的离子半径(0．062 nm)比Mn4+(0．053 nm)的半径大，且相对而言，c值增大比例更高，Ru离子取代Mn离子后的Mn0．875Ru0．125O2晶胞结构的对称性遭到一定程度的破坏，与文［17］报导一致．

图2 超胞体积与总能关系曲线图Fig．2 Total energy as function of super sell volume

表1 研究对象的点阵常数Tab．1 Lattice parameters of studied materials

2．2 能带分析

对晶体结构进行几何结构优化后，晶体结构到达稳定状态．然后用广义梯度近似方法处理交换关联泛函，并在计算中选取费米能级作为能量零点，可得纯金红石型MnO2以及Ru掺杂金红石型MnO2晶体沿着第一布里渊区的能带结构图．图3(a)为计算获得的金红石型MnO2费米能级附近的能带结构．从图3(a)可见，未掺杂Ru的金红石型MnO2能带中存在禁带．金红石型MnO2导带最低点在布里渊区高对称性的中心Γ处，价带最高点也在布里渊区高对称性的中心Γ处，因此属于直接带隙．计算得到的带隙值为0．493 eV，说明金红石型MnO2是一个直接间隙半导体．其带隙值与Tompsett等［23］计算的数值0．4 eV基本相符，但低于实验值2．23 eV［24］，这是由于采用密度泛函理论会低估能量的带隙［25］，不影响对问题的定性分析．导带底部在布里渊区高对称性的中心Γ处呈现为二重简并．图3(b)为金红石型MnO2掺杂Ru后费米能级附近的能带结构．

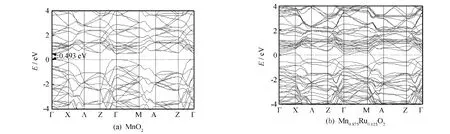
图3 能带图Fig．3 Energy band structures

从图3(b)可见，掺杂后导带和价带的位置都向低能方向发生了偏移，导带底由0．493 eV的位置降到了0．130 eV处，价带顶由0 eV的位置处降到了－1．018 eV处，价带的下降幅度大于导带的下降幅度，费米能级向导带偏移．导带底位于布里渊区高对称性的中心Γ处的简并度消失．对照图3(a)和(b)可知，未掺杂的金红石型MnO2难以导电．添加Ru后，在金红石型MnO2晶胞中形成了Ru离子取代掺杂，并且引入了施主型杂质能带，价带与导带发生部分交叠，说明材料的导电性能发生了改变，体现了出半金属特性［26］．杂质能带的出现，使得电子转移有了中转站更容易跃迁成功，因而提高了材料的导电性．由上可见，Ru原子添加后改变了金红石型MnO2的导电状态和性质．这从定性上解释了添加少量Ru就能获得性能良好的电极材料的原因．

2．3 电子态密度与电荷密度分析

为进一步了解金红石型MnO2掺杂Ru前后导电性质的变化，分别计算了 MnO2、Mn0．875Ru0．125O2总态密度和分态密度．纯金红石型MnO2的总态密度和O、Mn原子的分态密度如图4所示．其中，金红石型MnO2的总态密度可分为4个区域，位于价带的A、B区和位于导带的C、D区．图中沿着垂直方向的虚线代表费米能级位置．由图可见，能量范围处于－19．3～－17．1 eV的A区是由O2s轨道电子与Mn的3p轨道电子重叠产生，宽度约为2．2 eV，宽度较窄定域性强，属于深层能级处的轨道相互作用，对费米能级处附近的态密度分布影响较弱．B区域的能量范围为 －7．0～0 eV，主要为 O2p和Mn3d轨道电子占据，两者间的共振较为明显，由pd杂化形成了成键态．位于0．49～5．4 eV处的C区主要是由Mn3d和O2p杂化形成的反键态．处于8．3～25．0 eV的 D 区主要是由 O2p、Mn4s和 Mn3p轨道电子共同作用形成．

图4 MnO2电子态密度图Fig．4 Total DOSand PDOSof MnO2

Mn0．875Ru0．125O2的总态密度和 O、Ru、Mn 原子的分态密度如图5所示．对比可知，Mn0．875Ru0．125O2的态密度存在向低能方向移动的现象．Mn0．875Ru0．125O2的态密度在－0．53 eV处出现了尖峰．如图可见，能量范围位于－19．9～－17．4 eV的A区主要是由O2s轨道电子组成，Ru的4d，Mn的3d、3p轨道电子对其可忽略不计，宽度约为2．5 eV，属于深层能级处的轨道相互作用，对费米能级处附近的态密度分布影响较弱．在费米能级附近的B、C区，由于掺杂了Ru，引入了施主型的浅杂质能级，受Ru4d电子态影响，位于－0．7～－0．2 eV的区域出现了尖峰，并且尖峰与价带顶部只有0．3 eV能隙，此杂质能级尖峰突出，说明Ru4d电子态具有很强的局域特征．由于Ru的掺入，价带顶部和导带底部之间不再有间隙，出现了半金属特性．这一点也可以从图6看出．图6的(a)和(b)分别为金红石型MnO2掺杂Ru前后的(110)面的电荷密度分布图．通过对比可知，Ru原子周围的电荷密度较取代位的Mn原子周围的电荷密度显著变小，而且也没有之前的电荷密度对称，这是因为O原子得电子的能力比Ru原子强，Ru原子的价电子转移到O原子，Ru－O键呈现出离子键特征．

图 5 Mn0．875 Ru0．125 O2 电子态密度图Fig．5 Total DOSand PDOSof Mn0．875Ru0．125 O2

图6 研究体系的电荷密度分布图Fig．6 Plots of charge density contour of MnO2 and Mn0．875Ru0．125O2

2．4 载流子浓度分析

对电极材料而言，其导电的关键在于载流子的输运，它是由费米面附近的电子态决定的［13］．MnO2掺杂Ru前后的载流子输运能力的不同还需从量的变化方面进行分析．

根据半导体理论，Mn0．875Ru0．125O2的导带中的电子满足费米－狄拉克分布:

其中:EF为Fermi能级，Ei为导带底能级，kB为波尔兹曼常数，T为热力学温度．其导带电子浓度的计算公式为:

其中:gc(E)为导带底附近状态密度;V为超胞的体积，通过对总态密度(图4b)的积分计算可得(积分区间从导带底到费米能级);Mn0．875Ru0．125O2的电子浓度为5．86 ×1021cm－3，比添加 Ru 之前的2．99 ×1019cm－3增大了约200倍．根据载流子浓度的计算结果，同时结合图3和图4可以发现，掺杂Ru后的导电机制发生了显著变化，使得通过Ru添加后的材料导电性能显著增强．

3 结语

引入第一性原理的计算方法，采用密度泛函理论计算，获得了金红石型MnO2和Mn0．875Ru0．125O2晶体结构以及电子结构相关数据．计算结果表明:

1)金红石型的MnO2经Ru掺杂后，晶胞常数a、c增大，晶胞体积增大．相对而言，c值增大比例更高，说明Ru掺杂后使金红石型的MnO2出现一定程度畸变．

2)掺杂Ru后，金红石型MnO2的导带及价带向低能方向移动．导带底由0．493 eV的位置降到了0．130 eV处，价带顶由0 eV的位置处降到了－1．018 eV处，价带的下降幅度大于导带的下降幅度，费米能级向导带偏移．

3)掺杂Ru后，在金红石型MnO2晶胞中引入了施主型杂质能带，价带与导带发生部分交叠，导电性能发生了改变，出现了半金属特性，明显改善了MnO2电极材料的导电性能．

［1］Cheng F，Zhao J，Song W，et al．Facile controlled synthesis of MnO2nanostructures of novel shapes and their application in batteries［J］．Inorganic Chemistry，2006，45(5):2 038 －2 044．

［2］Tompsett D A，Parker SC，Bruce PG，et al．Nanostructuring ofβ －MnO2:the important role of surface to bulk ion migration［J］．Chemistry of Materials，2013，25(4):536 －541．

［3］Tompsett D A，Parker SC，Islam M S．Rutile(β－)MnO2surfaces and vacancy formation for high electrochemical and catalytic performance［J］．Journal of the American Chemical Society，2014，136(4):1 418 －1 426．

［4］Jiao F，Bruce P G．Mesoporous crystalline β － MnO2:a reversible positive electrode for rechargeable lithium batteries［J］．Advanced Materials，2007，19(5):657－660．

［5］Lee H Y，Goodenough JB．Supercapacitor behavior with KCl electrolyte［J］．Journal of Solid State Chemistry，1999，144(1):220－223．

［6］文建国，阮湘元，周震涛．Ru0．1Mn0．9Ox的制备与电化学赝电容特性研究［J］．稀有金属材料与工程，2009，38(5):930－934．

［7］Prasad K R，Miura N．Electrochemically synthesized MnO2－based mixed oxides for high performance redox supercapacitors［J］．Electrochemistry Communications，2004，6(10):1 004－1 008．

［8］Grupioni A A F，Arashiro E，Lassali T A F．Voltammetric characterization of an iridium oxide－based system:the pseudocapacitive nature of the Ir0．3Mn0．7O2electrode［J］．Electrochimica Acta，2002，48(4):407 － 418．

［9］Ye Z，Meng H，Sun D．New degradation mechanism of Ti/IrO2+MnO2anode for oxygen evolution in 0．5 m H2SO4solution［J］．Electrochimica Acta，2008，53(18):5 639－5 643．

［10］Chou J，Chen Y，Yang M，et al．RuO2/MnO2core－shell nanorods for supercapacitors［J］．Journal of Materials Chemistry A，2013，1(31):8 753－8 758．

［11］Kim S，Kim I Y，Patil SB，et al．Composition －tailored 2d Mn1－xRuxO2nanosheets and their reassembled nanocomposites:improvement of electrode performance upon Ru substitution［J］．Chemistry －A European Journal，2014，20(17):5 132 －5 140．

［12］刘志锋．钌锰二元涂层电极的电化学特性［D］．福州:福州大学，2011．

［13］刘雪华，邓芬勇，翁卫祥，等．Ru掺杂Sn基氧化物电极的第一性原理计算［J］．中国有色金属学报，2014，24(5):1 333－1 338．

［14］Kresse G，Furthmüller J．Efficient iterative schemes for ab initio total－energy calculations using a plane－wave basis set［J］．Physical Review B，1996，54(16):11 169－11 186．

［15］Zhu J，Wang X，Yi Z，et al．Stability of solid －solution phase and the nature of phase separation in Ru －Zr－Oternary oxide［J］．The Journal of Physical Chemistry C，2012，116(49):25 832－25 839．

［16］Wang X，Deng F，Tang Z，et al．The nature of phase separation in a Ru －Sn－O ternary oxide electrocatalyst［J］．Physical Chemistry Chemical Physics，2013，15(11):3 977 －3 984．

［17］王鑫，王欣，尹倩倩，等．Ru掺杂Zr基二元氧化物的第一性原理研究［J］．中国有色金属学报，2014，24(5):1327－1 332．

［18］Perdew J P，Burke K，Ernzerhof M．Generalized gradient approximation made simple［J］．Physical Review Letters，1996，77(18):3 865－3 868．

［19］Birch F．Finite elastic strain of cubic crystals［J］．Physical Review，1947，71(11):809 －824．

［20］Hu P，Huang Z，Hua W，et al．Effect of H2O on catalytic performance of manganese oxides in NO reduction by NH3［J］．Applied Catalysis A:General，2012，437/438:139 －148．

［21］Benyahia K，Nabi Z，Tadjer A，et al．Ab initio study of the structural and electronic properties of the complex structures of RuO2［J］．Physica B:Condensed Matter，2003，339(1):1 －10．

［22］Klug D D，Uehara K，Li Z Q，et al．Elastic properties of potential superhard phases of RuO2［J］．Physical Review B，2000，61(15):10 029－10 034．

［23］Tompsett D A，Middlemiss D S，Islam M S．Importance of anisotropic coulomb interactions and exchange to the band gap and antiferromagnetism ofβ －MnO2from DFT+U［J］．Physical Review B，2012，86(20):2 051 261－2 051 268．

［24］Sakai N，Ebina Y，Takada K，et al．Photocurrent generation from semiconducting manganese oxide nanosheets in response to visible light［J］．The Journal of Physical Chemistry B，2005，109(19):9 651 －9 655．

［25］Gunnarsson O，Lundqvist B I．Exchange and correlation in atoms，molecules，and solids by the spin－density－functional formalism［J］．Physical Review B，1976，13(10):4 274－4 298．

［26］黄昆，谢希德．半导体物理学［M］．北京:科学出版社．1958．