GM(1，1)模型在轨迹聚类中的应用

江艺羡，张岐山

(福州大学经济与管理学院，福建福州 350116)

0 引言

目前，移动对象轨迹数据的分析与研究应用在许多重要领域，如交通管理、气候监控等．移动对象轨迹聚类是移动对象轨迹分析的典型应用技术之一，其目标是寻找具有相同运动模式的轨迹，将相似度高的轨迹聚为一类［1］．

目前大多数轨迹聚类算法主要针对路网以及非路网形式的的移动对象．路网主要为受限的道路网络空间，分析移动对象的运行轨迹，有利于城市智能交通控制与决策［2］．非路网主要是自由空间，如进行台风监测与预报，或了解动物生活习性，迁徙特点等［3－5］．

到目前为止，基于移动对象轨迹的特殊性，为便于分析轨迹的局部信息，数据需要进行分割的预处理．自然界的大多数移动对象所产生的轨迹是相对平滑的曲线轨迹，因此，轨迹利用曲线表示更能符合实际意义．但由于曲线的函数表现形式比较复杂，因此现有轨迹分割方法主要采用基于线段的轨迹模型．轨迹数据在收集中出现的信息缺失或错误，使得到的数据为不确定数据，借鉴灰色GM(1，1)模型在‘贫数据’、‘小样本’数据中的优势，以及模型为平滑曲线的优越性，提出一种基于GM(1，1)模型的轨迹分段表示方法，实验结果表明本算法可以取得比线性拟合更好的结果．

1 GM(1，1)模型

灰色系统理论自建立以来，在生产、工程与科学等众多领域得到广泛的应用［6］．作为灰色预测理论的基本模型，GM(1，1)模型的应用也十分广泛．

定理1 设数据序列X(0)为非负序列，Y，B，r^=［a，b］T=(BTB)－1BTY，如定义2所述，则x^(0)k+1可由公式(2)求得．

GM(1，1)模型可以描述数据单调的变化过程，因此本文利用GM(1，1)模型的性质，通过拟合误差阀值限制轨迹压缩率，提取序列分段点，得到轨迹序列的分段表示．之后利用真实数据对本方法进行验证．

2 基于GM(1，1)模型的轨迹分段表示方法

定义3 (基于GM(1，1)模型的轨迹分段表示TR_GMPR)设有轨迹数据TR(0)={(x1(0)，y1(0))，(x2(0)，y2(0))，…，(x(n0)，y(n0))} ，在拟合误差阀值ε下，通过x坐标与y坐标的齐序列处理，它的分段函数表示为:

其中:［a1i，b1i］T与［a2i，b2i］T分别为x坐标与y坐标第i个子序列通过GM(1，1)模型所得到的参数列．(ti－1+1，ti)为x，y坐标第i个子序列第二个和最后一个数据在原序列的位置．

定义4 (轨迹分段表示的拟合误差［7］)设轨迹序列TR={(x1，y1)，(x2，y2)，…，(xn，yn)}，通过分段算法TR－GMPR得到轨迹的分段表示为:=(，，…，}．其中，={(，)，，)，…，()}，表示第 i个轨迹段．该 TR － GMPR 表示与原始时间序列之间的拟合误差定义为:

定义5 (轨迹分段表示压缩率［7］)设TR={(x1，y1)，(x2，y2)，…，(xn，yn)}，通过分段算法得到的轨迹为=(，，…，}，那么该算法的压缩率为 (1－×100%．

定义6 (轨迹平均方位向量TR［4］)设TR{(x1，y1)，(x2，y2)，…，(xm，ym)}为某一子轨迹，曲线中某点的速度方向为该曲线对应点的切线方向．根据该性质，定义子轨迹在点k处(k=1，2，…，m)的切向量为子轨迹在该点的方向向量TRk=(x'(k)，y'(k)) ，则子轨迹的平均方位向量为TR:

定义7 (轨迹簇平均方位向量CTR［4］)设轨迹集合为CTR，NCTR表示轨迹集合中轨迹的个数．簇中任一轨迹TRi(i=1，…，NCTR)的平均方位向量为TR，则轨迹簇的平均方位向量CTR定义如下:

3 实验及结果分析

采用两个实验验证算法的有效性(表1)．在实验1中，采用2012年的飓风［3］作为实验数据．分析本文TR_GMPR算法轨迹划分压缩率与拟合误差的情况．在实验2中，采用1950—2011年的飓风以及Deer［3］作为实验数据．分析TR－GMPR算法在基于密度的聚类分析中的可行性．

表1 实验数据集长度Tab．1 Length of the experimental databsets

3．1 实验1结果及分析

轨迹压缩率随误差阀值的变化情况见图1．轨迹拟合误差随压缩率的变化情况见图2．

图1 误差阀值与压缩率Fig．1 Error threshold and compression ratio

图2 压缩率与拟合误差Fig．2 Compression ratio and fitting error

从图1可见，误差阀值越大，压缩率越高．曲线在上升过程中，有出现上下波动的情况，主要原因是在进行分段过程中，误差阀值不同，曲线分割点亦不同，分割成的子轨迹长度的变化，引起子轨迹个数的变化，使得压缩率出现波动．从图2可见，随着压缩率逐渐变大，拟合误差的变化相对比较迅速．

飓风拟合图(见图3)随着压缩率的变大，拟合误差越明显．在压缩率为75．91%时，拟合数据(虚线)与原轨迹数据(实线)的重合率较高．当压缩率达到88．56%时，拟合图与原数据的重合率较低，但拟合图形的曲线性质依然能较好地表达原数据的变化情况．

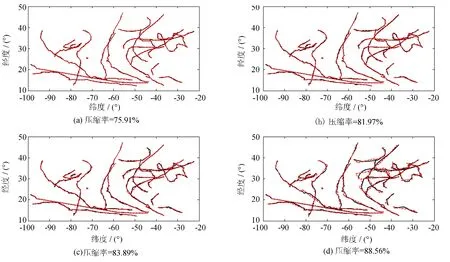
图3 2012飓风拟合图Fig．3 Fitting－ figures of hurricane in 2012

3．2 实验2结果及分析

实验2采用基于密度的聚类算法法DBSCAN［3］，算法的定义参考文献［3］．该算法需要输入三个参数(近邻半径Eps，近邻个数k，聚类个数class)．算法相关性见图4．

图4 DBSCAN算法参数相关性Fig．4 The correlation between parameters of the DBSCAN algorithm

图4显示，对于不同的紧邻个数k，飓风聚类个数class随着近邻半径Eps的变大，先变多后变少，而Deer则随着近邻半径的变大，聚类数变多．主要是动物运动的点相对比较没有规律．近邻半径较小时，一部分点被定义为噪声，近邻半径变大后，一部分噪声点参与聚类．下文聚类选择参数为:1)飓风:k=30，Eps=11，class=8;2)Deer:k=30，Eps=65，class=3．

飓风轨迹分段表示平均压缩率为84．54%．对压缩后的轨迹进行聚类，生成轨迹的特征轨迹［4］．为方便分析轨迹的变化情况，采用四个方向(东北EN，西北WN，西南WS，东南ES)对各个聚类结果进行细化．第i个聚类中，总轨迹数为Ni，各个方向轨迹数为NiEN，NiWN，NiWS，NiES，显示轨迹数超过10%的Ni方向特征轨迹，见图5．

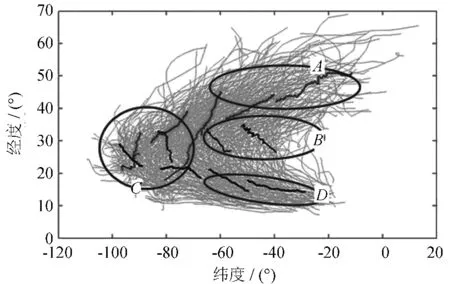
图5 1950－2011年飓风特征轨迹图Fig．5 Characteristic trajectories of hurricane between 1950 and 2011

图5中主要分成四个部分，D为飓风起点区域，B、C为飓风运动区域，A为飓风运动末端区域．

1)D区域为飓风运动起点区域，运动方向比较一致，因此主要代表轨迹比较单一．

2)D区域部分飓风直接通过B区域进入A区域，因飓风运动方向转变的角度，B区域理论上会出现多条代表轨迹．而本文B区域的两条相距较远的代表轨迹也验证了该假设．

3)C区域为，飓风运动至C区域或者停止，或者转换方向，在该区域运动情况比较复杂．本文方法结果显示，在C区域主要特征轨迹方向有东北，西北，西南三个方向，代表轨迹数量多，长度短，纵横交错，进一步显示飓风在该区域变化多端的特性．

4)A是飓风运动末端，从B或C区域运动方向转变后的轨迹区域，相对而言飓风风力较小，飓风数量远低于起点区域D．并且轨迹运动方向相对比较一致，红色曲线所代表的主要轨迹更是印证这点．

相关文献实验结果见图6．文献［1］在区域B中轨迹的运行方向不符合实际意义．文献［4］在B区域，特征轨迹较不明显，C区域不能体现飓风运动的复杂性．文献［4］在C部分能体现飓风运动的复杂性，但长轨迹1与轨迹3的运行方向在起始点区域有部分相似．文献［5］起始点区域特征轨迹与实际相差甚远．

图6 各参考文献实验结果(飓风)Fig．6 Experiment results of all references(hurricane)

动物Deer1995的实验结果见图7，图7(a)为聚类后采用四个方向(东北EN，西北WN，西南WS，东南ES)描述的聚类结果图．由此可见动物运动的复杂性．动物迁徙的特性，用热点区域的形式表示最佳，若以轨迹表示，则如图7(b)所示．文献［4］中，忽略A区域对动物迁徙轨迹的影响．文献［3］算法稳健性较好．能将动物活动比较频繁的地方聚为一类，但却忽略了局部区域的活动特征．本文方法能在区域A显示动物活动轨迹．但因为动物运动轨迹相对比较复杂，特征轨迹受平均运动方向的影响，在B、C区域的两端运动轨迹也稍微偏离实际情况．

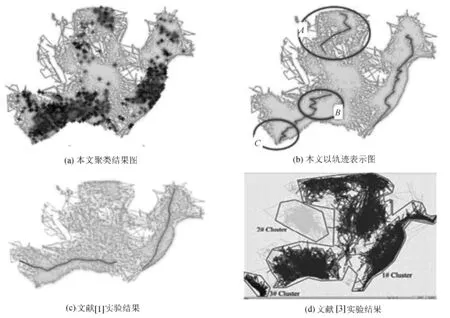
图7 聚类结果与参考文献结果Fig．7 Experiment results of clustering and references

4 结论

灰色系统具有所需样本数据少且基于计算的优点，已被广泛应用于各个领域，特别是在小样本、贫信息的不确定系统或缺乏数据的情况下，得到了较为成功的应用．移动对象轨迹数据因传输延迟或缺失而具有不确定性，或因实验成本或实验重复性使得获取的数据较少．基于这些情况，本文采用GM(1，1)模型对轨迹数据进行分段表示，之后利用密度聚类算法进行聚类分析，多组实验表明了本文方法的可行性与有效性．但该算法也存在一定的不足，GM(1，1)模型参数受初始值的影响较大，合适的初值才有更好的拟合结果;模型的单调性质，对于相对比较复杂的轨迹分割效果相对比较不理想．

［1］Lee J G，Han Jiawei，Whang K Y．Trajectory clustering:a partition－and－group framework［C］//Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data．New York:ACM Press，2007:593 －604．

［2］赵建军，陈滨，杨利斌，等．一种新的轨迹聚类及有效性评价方法［J］．系统仿真技术，2012，8(4):305－309．

［3］袁冠，夏士雄，张磊，等．基于结构相似度的轨迹聚类算法［J］．通信学报，2011(9):103－110．

［4］陈锦阳，宋加涛，刘良旭，等．基于改进Hausdorff距离的轨迹聚类算法［J］．计算机工程，2012，38(17):157－161．

［5］Zhang Lei，Yang Guang，Wang Zhichao，et al．Trajectory clustering based on spatial generalization［J］．Jouranl of Information＆ Computational Science，2012，9(2):315－321．

［6］刘思峰，党耀国，方志耕，等．灰色系统理论及其应用［M］．北京:科学出版社，2010．

［7］詹艳艳，徐荣聪，陈晓云．基于斜率提取边缘点的时间序列分段线性表示方法［J］．计算机科学，2006，33(11):139－142．