囚徒困境博弈策略在社团网络中的演化

陈雅姗，郭文忠

(1．福州大学数学与计算机科学学院，福建福州 350116;2．福州大学至诚学院，福建福州 350002)

0 引言

无论是自然界还是人类社会，合作现象都是普遍存在的［1］．但是根据自然选择的适者生存进化原理，生物个体是自私自利、追求利益最大化的，这将导致个体之间相互背叛，那么自然界中的合作现象是如何存在的?科学家们将进化博弈论与复杂网络相结合，深入探究合作行为的产生机理及演化情况．复杂网络是近年来兴起的一门交叉学科，可以准确描述许多自然界和社会中的系统，并已引起国内外专家学者们的研究兴趣，取得一定的研究成果［2－4］．但其平均路径却比较长;小世界网络虽然兼具小的平均路径和高聚类特性，但其度分布却不服从幂律分布．1999年Barabási和Albert在总结这些网络模型缺陷的基础上，构建了度分布服从幂律分布的无标度网络模型［5］(BA模型)，此模型能更好地刻画实际网络，因此在之后的复杂网络研究领域里，无标度网络占据了主导地位．

近年来大量的研究表明许多真实网络都有一个相同的特征——社团结构，而BA模型无此特性．社团结构就是一个大网络由多个小的“群”或者“社团”所组成，同一个“群”内的节点连接紧密，不同“群”之间的节点连接稀少［6］．社团结构在真实系统中代表着不同的含义:在社交网中，不同“群”代表着不同的领域、职业、年纪等［7］;在引文网中，不同“群”体现了不同的研究领域［8］．基于此，有专家提出了兼具无标度和社团结构特性的社团网络［9－10］．

目前关于社团网络的研究工作还比较少，本文基于社团网络，采用“囚徒困境”模型来模拟个体之间的合作演化情况，重点在于讨论社团网络中，具有什么特点的网络拓扑性质能更好地促进合作的涌现和维持，并深入探讨这些网络拓扑环境促进合作产生的内在机制．

1 模拟方法

1．1 网络模型

首先生成一个网络规模为N且具有社团结构的无标度网络［10］:先形成G(G≥2)个社团，每一个社团都包含m0(m0＞1)个节点．让初始的m0×G个节点彼此相互连接，在之后的每一时间步长里，每个社团都添加一个新节点和m条边(m＜m0，且网络平均度=2m)．先指定其中的n条边连接到同一个社团里(0≤n≤m)，剩下的m－n条边连接到随机选取的其它社团中．所有边的连接都按照BA无标度网络的度优先连接原则．定义了社团强度Q，它体现同一社团内部节点相互之间连接的紧密程度．其中Q与m和n具有简洁的关系形式:

1．2 “囚徒困境”模型

囚徒困境是博弈论中的经典模型．在该模型中，两个个体同时决定背叛或者合作，如果甲选择背叛而乙选择合作，那么甲得到的收益为T，而乙将获得收益为S;反之亦然，如果双方都合作获得R收益，都背叛获得P收益．该模型中T＞R＞S＞P，2R＞S+T［4］．显而易见，无论乙采用何种策略，甲认为采用背叛总是对本身最有利，相同的逻辑对对方同样适用．根据适者生存进化原理，这将导致个体之间相互背叛，但是在自然界合作现象仍普遍存在，生物个体似乎可以克服自身的私利，采取有利于所有个体的策略．

1．3 演化规则及参数设置

参考传统演化过程模拟的参数设置，具体参数取值为:R=1，T=b=1～2，P=S=0，N=10000，G=10，m=4，0≤n≤m，m0=5．网络中的每个节点代表参与博弈的每个个体，个体间如果发生交互关系就连接该两节点．初始化网络时，各节点合作和背叛策略的分布概率相同．为降低涨落引起的误差，每次的模拟都是先演化30 000代，再对之后的2 000代取平均，并模拟50次，最后对所得的50次结果进行平均处理．模拟过程进行的是同步演化规则，每一代的演化都包括如下两过程:

1)个体都与自身的所有邻居产生博弈，并获得收益值．令si代表个体i所选择的策略，其取值为:

和所有邻居产生博弈时，个体i都选择同一种策略，可得到经过每一代博弈后个体i的总收益值为:

其中:fi表示在博弈时个体i的邻居中采取合作策略的个体数目;ki表示个体i的度，即个体i有ki个邻居．

2)当个体i要更新策略时，从ki个邻居中随机选取邻居j，当Ei＜Ej时，在下一代个体i将以概率

采取邻居j的策略．其中k＞取ki和kj的较大者［11］．

为了定量分析合作行为的变化趋势，引入群体合作频率ρc，其定义为在进化博弈进入稳定状态后，合作个体占总群体数目的比例．

2 模拟结果及讨论

2．1 社团强度对合作演化的影响

不同社团强度对合作演化情况的影响如图1所示．由图1(a)可见，与BA无标度网络相比，具有社团结构的无标度网络更能促进合作行为的产生．同时，社团强度Q值的大小明显影响了群体的合作情况．当Q为0．9时，一直都保持着较高的合作率，而当Q为0．3时的合作情况却不如Q为0．1时的情况，因此本文固定了背叛诱惑b值的大小，考察群体合作频率随Q的变化关系．图1(b)是网络平均度=8，背叛诱惑b=1．8时，群体合作率随Q的变化曲线．图示表明，合作率并不随Q的改变成线性关系，而是当Q较小或较大时，有利于合作的产生，当Q在0．5左右时，大大降低了系统的合作率．为了更详尽地探究不同社团强度的网络拓扑环境如何影响系统合作的演化，本文考量了网络的另一个重要指标:聚类系数C．

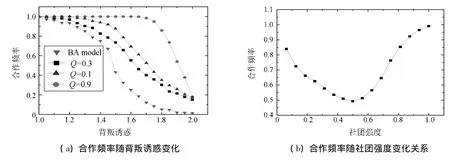
图1 社团强度对合作演化的影响Fig．1 Community strength influences the evolution of cooperation

2．2 网络聚类系数对合作演化的影响

网络聚类系数随社团强度的变化情况如图2(a)所示，曲线趋势与图1(b)相似，即Q较大或较小时，网络具有较大聚类系数，当Q为0．5左右时，聚类系数较小．聚类系数的其中一种定义为:C=(3×三角形数目)角形数目 (5)其中:角形是一个节点与另外两个节点相连形成的夹角形状．当Q在0．5左右时，表示刚产生的新节点所引入的m条边中，有一半是与节点所在的社团成员连接，另一半则与其他社团的成员连接，如此引进的m条边很难为网络增加新的三角形;而当引进的m条边都与节点所在的社团成员连接，或者只与其他社团成员连接时，将有利于新三角形的形成，也将提高网络的聚类系数．三角形是最稳定的几何结构单元，从公式(3)可知，当构成三角形的三个节点都是合作者时，它们彼此的收益达到最大，处于相对稳定状态，并将慢慢形成一棵越来越大越紧密的稳定合作树，共同抵制背叛者入侵;而当三个节点都是背叛者时，它们自身的收益降到最低，此时背叛者难以生存，很快又采取合作策略．无标度网络虽然具有度幂律分布的特点，但其网络聚类系数却接近于零，事实上，大量现实网络(如社会关系网络)都有较高的聚类系数．此属性较易理解，比如，一个成员的朋友关系网络中，他的朋友彼此之间也比较容易认识而成为朋友．

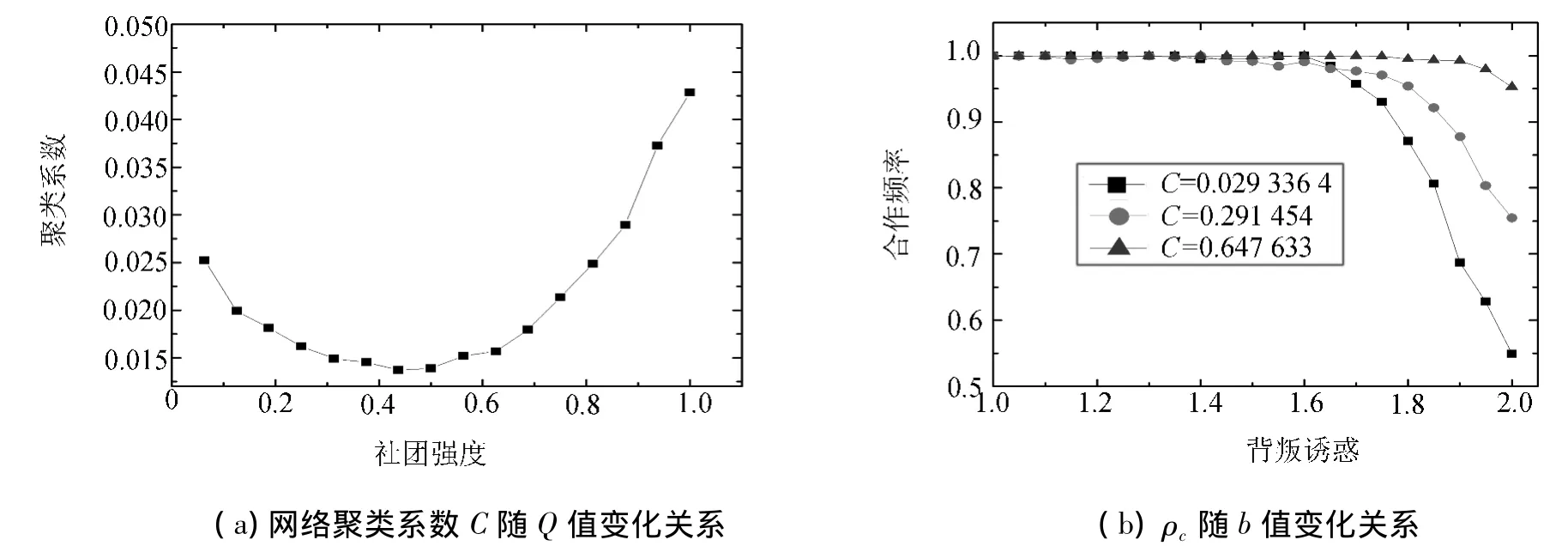
图2 网络聚类系数对合作演化的影响Fig．2 Clustering coefficient influences the evolution of cooperation．

为了更接近真实网络，本文按照文献［12］构建网络的方法，生成了能调节聚类系数的社团网络．具体的网络生长过程如下:引入一个新节点i，在完成一次优先连接后以几率POT(probability of triangle formation)组成一个三角连接，再以几率1－POT完成优先连接，直到连完m条边，继续重复此过程引入另一新节点，直到生成一个节点数目为N的网络．可见，能够通过调节POT概率来改变网络聚类系数．图2(b)是三种不同C的社团网络中，群体合作率ρc与背叛诱惑b值的关系图，网络的社团强度固定为0．9．由图可见:具有较大聚类系数C的网络，更能促进群体合作行为的涌现．

2．3 网络平均度对合作演化的影响

度是复杂网络研究当中的一个重要指标，网络中一般用ki表示节点i的度，即节点i与ki个邻居节点有直接的连线，网络平均度即为每一个节点度的平均值，一般用表示．图3是具有相同社团强度，却有不同平均度的社团网络中系统合作率ρc与背叛诱惑b值的关系图．由图3可见，在社团网络中，平均度越大，反而阻碍了群体合作行为的出现．主要是因为网络中的“中枢节点”(“中枢节点”指网络中度比较大的节点)之间的直接连线能提高系统合作率［13］．当网络平均度较小时，“中枢节点”的地位相对稳固，“中枢节点”之间的连线比例较高．随着平均度增加，将有更多的“老节点”(“老节点”指生成网络时较先引入的节点)开始加入“中枢节点”行列，并且在网络生成过程中，这些“老节点”之间没有连线，之后的演化中也无法再相互连线，必将降低“中枢节点”之间直接连线的比例，因此导致了网络平均度越大反而降低了群体合作率．

图3 不同平均度下ρc随b的变化Fig．3 ρc vsbon different values of k

3 结论

将囚徒困境博弈策略与社团网络相结合，探讨社团网络的拓扑环境怎样影响群体合作行为的演化．计算机模拟结果显示，社团强度Q明显影响了群体的合作情况，Q较小或较大时都能激励合作行为的涌现，维护合作现象的持续，当Q为0．5左右时，系统合作率明显降低;系统合作行为在不同聚类系数的社团网络中演化情况不同，有明显聚类效应的网络更有利于合作行为的演化;当网络平均度增大时，反而阻碍了合作行为的出现．

［1］Gintis H．Game theory evolving［M］．Princeton:Princeton University，2000．

［2］Hu Cheng，Yu Juan，Jiang Haijun，et al．Synchronization of complex community networks with nonidentical nodes and adaptive coupling strength［J］．Physics Letters A，2011，375(5):873 －879．

［3］荣智海，吴枝喜，王文旭．共演博弈下网络合作动力学研究进展［J］．电子科技大学学报，2013，42(1):10－19．

［4］陈雅姗．影响力异质性影响群体合作的演化［J］．福州大学学报:自然科学版，2010，38(5):653－656．

［5］Barabási A L，Albert R．Emergence of scaling in random networks［J］．Science，1999，286(5 439):509 －512．

［6］Kim Y，Son SW，Jeong H．Link rank:finding communities in directed networks［J］．Physical Review E，2010，81(1):95－102．

［7］李晓佳，张鹏，狄增如，等．复杂网络中的社团结构［J］．复杂系统与复杂性科学，2008，5(3):20－40．

［8］张聪，沈惠璋．网络自然密度社团结构模块度函数［J］．电子科技大学学报，2012，41(2):185－191．

［9］Kashtan N，Alon U．Spontaneous evolution of modularity and network motif［J］．Proceedings of the National Academy of Sciences of the United States of America，2005，102(39):13 773－13 778．

［10］邓智龙，淦文燕．复杂网络中社团结构发现方法［J］．计算机科学:2012，39(6A):103－108．

［11］Santos F C，Pacheco J M．Scale－free networks provide a unifying framework for the emergence of cooperation［J］．Physical Review Letters，2005，95(9):98－104．

［12］Holme P，Kim B J．Growing scale－free networks with tunable clustering［J］．Physical Review E，2002，65(2):1 －4．

［13］Chen Yashan，Lin Hai，Wu Chenxu．Evolution of prisoner＇s dilemma strategies on scale － free networks［J］．Physica A －Statistical Mechanics and its Applications，2007，385:379－384．