后张法预应力混凝土简支梁预应力摩擦损失的理论研究

黄 颖，房贞政，高 杰

(1．福建船政交通职业学院建筑工程系，福建福州 350007;2．福州大学土木工程学院，福建福州 350116)

0 引言

后张法预应力混凝土构件在正常使用极限状态设计计算中，预应力损失的计算与分析是十分重要的，各国规范对此都给出了详细的计算公式［1－3］，在分项预应力损失计算中，预应力钢筋与管道壁之间的摩擦损失约占总损失的20%［4］，多项实测试验表明［5－6］，预应力管道摩擦损失实测值相比按照现有规范计算的理论值大．规范中对于预应力钢筋弯曲孔道的摩擦损失得到的公式是基于赫兹(Hertz)理论中的光滑非协调接触［4］，认为弯曲孔道处对混凝土产生的径向压力是均匀的，预应力钢筋和混凝土接触面产生均布正应力或者球状分布应力，如图1(a)所示，得到的摩擦损失公式为:

但是事实上，预应力钢筋在张拉时，特别是在弯曲孔道处对混凝土产生较大的径向压力，使此处的混凝土产生局部变形，因此，此处的预应力钢筋和混凝土接触面之间接触正应力不能被简化为均布正应力或者球状分布应力，应该是一种非均匀分布应力［7－8］，如图1(b)所示．针对连续型布筋和分段型布筋两种型式，认为弯曲孔道处的径向压力p是非线性分布，也就是不均匀分布，利用库仑摩擦定律，预应力钢筋和孔道之间的摩阻力正比于接触应力，接触应力通过平面几何分析与径向压力p建立关系，因此推得预应力钢筋和孔道之间的摩阻力也是非线性的，以此推导出任意应力分布情况下弯曲孔道摩擦阻力公式．通过对比计算分析，利用本文推导的公式计算的摩擦损失值相比规范公式，精确度更高，与试验实测值［7－9］更接近．

图1 弯曲孔道正应力比较分布图Fig．1 Bending normal stress distribution comparison graph

1 连续型弯曲孔道预应力损失计算公式研究

如图2所示，在不均匀应力分布情况下，设混凝土和预应力钢筋接触面的接触应力为q(θ)，方向如图所示，指向圆心，则圆弧微圆段d l产生的轴向力为q(θ)d l，则根据库仑定律，管道摩擦力为μq(θ)d l，方向为圆弧切向方向．设圆弧的圆心角度为θ，圆弧半径为R，预应力钢筋一端的张拉力为F，另一端为接触内力F－Fs，Fs为管道摩擦造成的预应力损失，混凝土产生的径向压力为Fj，管道摩擦力为Fm，其中:

图2 弯曲孔道预应力钢束受力示意图Fig．2 Prestressed steel of bending force diagram

如图2(c)所示，建立直角坐标系，以预应力钢筋作为研究对象，建立受力平衡方程．沿x轴方向有:

沿y轴方向有:

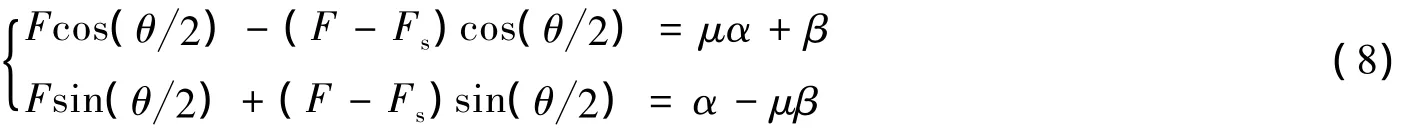
联立方程求解，得到关于x，y的耦合方程:

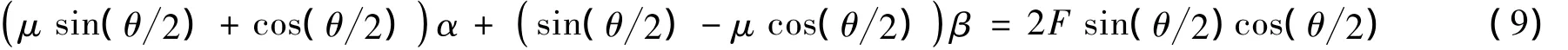
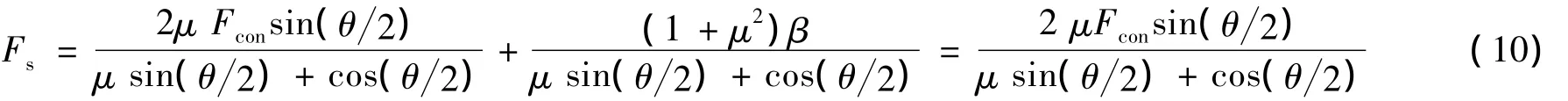
通过对比本文公式推导过程与规范公式推导过程可以看出，规范公式对管道摩擦损失的推导分析忽略了高阶微分段内张拉力对径向压力的影响，也近似地取2Fconsin(dθ2)≈2Fcon(dθ2)，而本文公式的推导没有忽略这两项的影响，精确地考虑了这两项的误差．

2 分段型弯曲孔道预应力损失计算公式研究

前述公式的推导是基于连续型圆弧，以弧段为单位进行分析，对于分段连续型弯曲孔道，需要对孔道进行分段讨论，如图3所示．设第一段起点的预应力值为F1，终点的预应力值为F'1，经过一段中间直线段后，第二段弧段起点的预应力值为F2，终点的预应力值为F'2，由公式(10)可知:

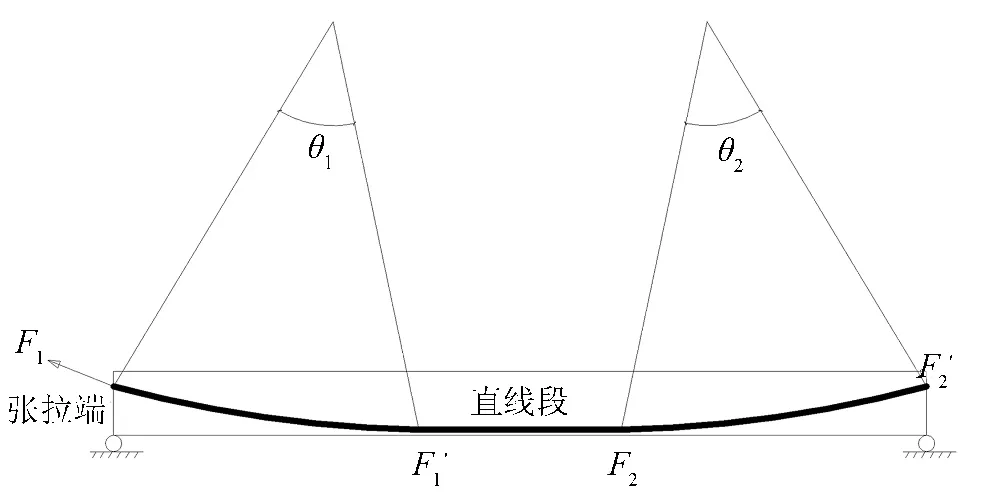
图3 分段型布筋示意图Fig．3 Sectional type reinforcement schematic diagram

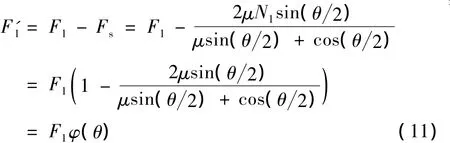
第一段终点的预应力值为:F'1=F1－Fs(θ1)=F1φ(θ1)，第二段终点的预应力值为F'2=F2－Fs(θ2)=N2φ(θ2)，经过第一段圆弧管道后，理论上有F1'=F2，则F2'=N1φ(θ1)φ(θ2)与连续型圆弧比较，若 θ= θ1+ θ2，连续型圆弧有:F'2=F1φ(θ);分段型圆弧有:F'2=F1φ(θ1)φ(θ2)．

在对患者进行采样之前，如果患者进行运动、饮食或者服用药物的话，那么就可能会对检验结果产生一定会的影响，导致检验数据出现偏差。因此，在对患者进行采样之前，应当要求患者不要进行运动、饮食以及服药，确保患者的状态稳定后再进行采样，确保样本采集质量，防止因样本问题而导致检验出现偏差。

由公式(11)可知:

所以，由公式(12)可知，在不考虑孔道偏差的情况下，分段型圆弧的剩余预应力大于连续型圆弧，说明分段型圆弧的预应力损失值小于连续型圆弧，即:Fs(θ)＞Fs(θ1)+Fs(θ2)．

对于规范［1］预应力摩擦损失公式，由于是指数型公式，当连续型圆弧的圆心角等于分段型圆弧各圆心角之和，分析结果如表1所示．

表1 分段型圆弧与连续型圆弧预应力损失比较Tab．1 The prestressing loss comparison of sectional type and continuous type

从表1可知，当连续型圆弧的圆心角等于分段型圆弧各圆心角之和时，对于规范［1］给定公式，两者计算的预应力摩擦损失值相等，但是对于本文推导公式，通过分析可知，连续型圆弧的预应力摩擦损失值大于分段型圆弧．

将以上分析结论汇总，管道摩擦损失采用本文推导数学公式，管道位置偏差的摩擦阻力计算仍然采用规范公式，即本文建立的预应力钢筋张拉摩阻损失计算公式为:

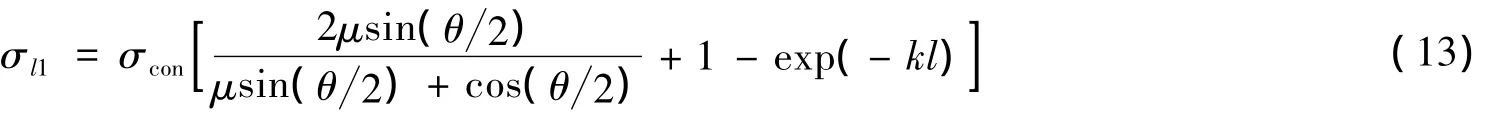
式中各参数意义与规范公式相同．

3 张拉摩擦预应力损失计算分析与比较

1)本文推导公式与规范公式的计算比较．为了证明本文推导公式的适用性，选取一系列的弯曲孔道圆心角，分别根据规范［1］公式和本文建立的弯曲孔道计算公式计算预应力损失值，取预应力钢筋与管道壁的摩擦系数μ为0．15，管道每米局部偏差对摩擦的影响系数k为0．001 5，φ(θ)为预应力钢筋经过管道摩擦后的预应力余值系数，定义预应力管道摩擦损失系数为γ，则γ=1－φ(θ)．根据表1中给出的规范和本文推导的预应力余值系数公式，计算预应力管道摩擦损失系数，计算结果如表2和图4所示．对于分段型圆弧，定义其分为两段，每段的圆心角为连续型圆弧圆心角一半．

2)有限元建模分析比较．利用有限元分析软件ANSYS分别建立预应力钢筋连续型和分段型张拉模型，定义不同的圆心角，利用实常数TAUMAX定义等效剪应力最大值，当等效剪应力达到最大值TAUMAX，预应力钢筋就会发生滑动［10］，以此进行预应力钢筋摩擦滑移控制．定义本文推导公式计算的预应力管道摩擦损失系数与规范公式计算值的误差为(γ本文－γ规范)/γ规范，将各项计算分析值汇总于表2．

表2 预应力管道摩擦损失系数γ计算比较分析表(γ无量纲)Tab．2 Comparative analysis of the friction loss coefficient in prestressed pipe

从表2和图4可以看出:

1)对于连续型圆弧孔道，当圆心角小于40°时，按照规范公式和本文推导公式的计算结果基本一致，但是当圆心角大于40°后，本文推导公式的计算结果明显大于规范计算公式，当圆心角为100°时，两者相差达到30%，而且这一数值随着圆心角的不断增大而增大．

2)根据规范公式计算的连续型圆弧和分段型圆弧孔道摩擦损失相同，但是对于本文推导公式，连续型圆弧的预应力摩擦损失值大于分段型圆弧，计算分析进一步验证了前述公式的推导．

3)根据本文推导的分段型孔道摩擦损失系数小于连续型，但是仍然大于根据规范公式计算的孔道摩擦损失系数，当圆心角为100°时，两者相差达到4%．

4)通过建立有限元模型进行对比分析，表明本文推导公式的计算结果与有限元建模分析结果更加接近．

从以上分析可以看出，当孔道圆心角较大时，规范公式推导中的高阶微分的影响是不能忽略的．

图4 预应力孔道摩擦损失系数γ比较图Fig．4 Comparison chart of the friction loss coefficientγ

4 结论

针对连续型预应力钢筋和分段型预应力钢筋两种布筋形式，在不考虑孔道偏差的情况下，推导了预应力钢筋孔道摩擦损失的计算公式，并且通过实例对本文推导公式和规范公式进行对比分析，最后通过有限元建模进行验证，得出如下4点结论．

1)根据本文推导公式计算的结果明显大于规范公式计算结果，而且随着预应力钢筋曲线布置圆心角的增大，两者计算结果差值不断加大．

2)从本文推导公式和有限元分析结果可以看出，连续型布筋和分段型布筋的摩擦损失不同，连续型圆弧的预应力摩擦损失值大于分段型圆弧，而规范计算公式两者并没有区别．

3)为了能准确估计预应力钢筋管道摩擦损失，特别是预应力钢筋布置圆心角较大的大跨度桥梁，在条件许可的情况下，尽可能地对摩擦系数和偏差系数进行实测．

4)为了保证实际施工中预应力钢筋发挥的有效程度，施工中可以采取两端张拉、采用超张拉程序［4］、预应力表面涂润滑剂等措施减少预应力管道摩擦损失．

［1］中华人民共和国交通部．JTGD62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．北京:人民交通出版社，2004．

［2］美国国家高速公路和交通运输协会．美国公路桥梁设计规范［S］．辛济平，译．北京:人民交通出版社，1998．

［3］Comite Euro－International du Beton and the Federation International de la Preconstrainte．Model code for concrete structures 1990［S］．Paris:［s．n．］，1990．

［4］房贞政．预应力混凝土结构［M］．2版．北京:中国建筑工业出版社，2014．

［5］王宏．预应力筋与孔道壁之间的摩擦引起的预应力损失［J］．暨南大学学报:自然科学版，2005，26(1):100－102．

［6］刘鹏飞，赵启林，江克斌，等．大跨度混凝土桥梁预应力摩擦损失的理论研究［J］．工业建筑，2011，41(10):64－67．

［7］张元海，刘世忠．后张法预应力混凝土梁钢束预应力损失研究［J］．中国公路学报，2002，15(2):76－78．

［8］Kim Y J，Green M F，Wight R G．Bond and short－term prestress losses of prestressed composites for strengthening PCbeams with integrated anchorage［J］．Journal of Reinforced Plastics and Composites，2010，29(9):1 277 － 1 294．

［9］Zhang Kaiyin，Cheng Chen．Analysis on prestress loss caused by friction in curved duct in the design of prestressed concrete structure［C］//The 4th International Symposium on Life Time Engineering of Civil Infrastructure．［s．l．］:Science Press，2009:701－705．

［10］王新敏．ANSYS工程结构数值分析［M］．北京:人民交通出版社，2007．