（u，v）幂等矩阵与本质（m，l）幂等矩阵

林志兴，杨忠鹏，陈梅香，2，陈智雄，陈少琼

（1．莆田学院数学学院，福建 莆田 351100；2．福建师范大学数学与计算机科学学院，福建 福州 350007；3．华南理工大学数学学院，广东 广州 510640）

0 引言

设Fn×n为数域F上n×n矩阵的集合，C为复数域，In为n×n单位矩阵．r（A）和mA（x）分别表示A∈Fn×n的秩和最小多项式．设N为非负整数集合且［p1，…，pk］为非零的p1，…，pk∈N的最小公倍数．使λk＝1，（λ∈C），成立的最小正整数k称为单位根λ的阶，记为．总约定ε0，ε1，…，εu－v－1为所有u－v次单位根，这里u，v∈N，u＞v．

若正整数u∈N使Au＝A，称A为u幂等的．文［1－7］研究了u幂等矩阵与秩的有关问题．若u，v∈N，u＞v，使Au＝Av，称A为（u，v）幂等矩阵［8－9］．记Pn（u，v）（F）＝ ｛AA∈Fn×n，Au＝Av｝．显然Pn（u，0）（F）、Pn（u，1）（F）分别是通常的u幂幺、u幂等矩阵集合．文［8］、［10］给出了（u，v）幂等矩阵秩的等式．

命题1［9］设A∈Fn×n，u，v∈N 且u ＞v，则

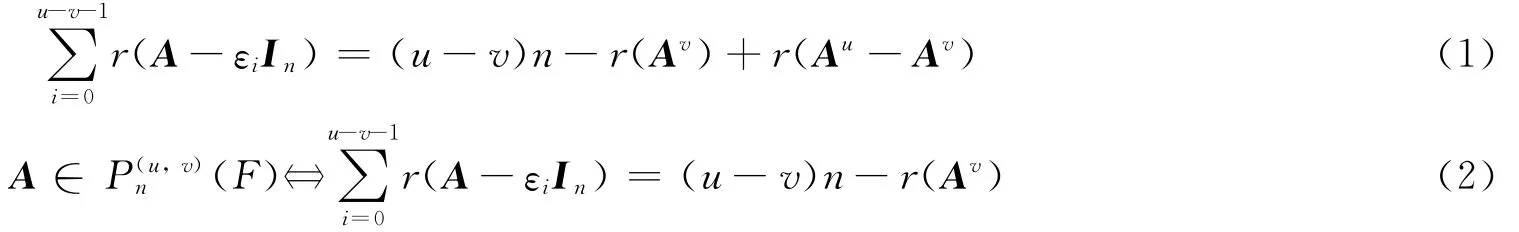
命题2［12］设A∈Pn（u，v）（F），则A相似于准对角矩阵diag（M，ε0In0，ε1In1，…，εu－v－1Inu－v－1），其中：M为由型Jordan块构成的准对角矩阵，且它们最大阶数不超过v；ni＝n－r（A－εiIn），i＝0，1，…，u－v－1．

由文［2］得到了3幂等矩阵的一个重要性质：

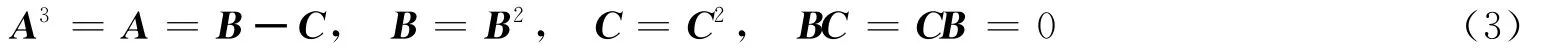
显然幂等矩阵是3幂等的．为了区别这种情况，文［13－14］给出了本质3幂等矩阵的定义，即满足A3＝A≠A2（即（3）式中B，C都非零）的A．

设A∈Fn×n，若有最小正整数m使m＞l（∈N）且Am＝Al成立，称A为本质（m，l）幂等矩阵，记A∈EPn（m，l）（F）．可 见 例1中A∈EP3（3，2）（F）为本质（3，2）幂等的．由文［15－16］知EPn（m，0）（F）、EPn（m，1）（F）分别为本质m幂幺矩阵、本质m幂等矩阵集合．

由文［9］知幂等性与数域扩大无关，因此当A∈Fn×n时，A∈Pn（u，v）（F）（EPn（m，l）（F））当且仅当A∈Pn（u，v）（C）（EPn（m，l）（C））．这样只要考虑A∈Cn×n．

以下总设A∈Cn×n的Jordan标准形满足

当ni＝1时，约定Jor dan块是1阶矩阵；因此1阶幂零的Jor dan块N1＝0∈C．

满足r（Al）＝r（Al＋1）的最小l∈N 称为矩阵A 的指数，记ind A［17－18］．文［15－16］证明当A∈Cn×n所有特征值为零时，A∈EPn（m，l）（C）⇔l＝n1且m＝l＋1；此时l＝n1＝ind A（由文［17］知ind A＝0⇔A是可逆的；当A∈Pn（u，v）（C）且r（A）＝n时，必有Au－v＝In．由于文［5］、［19］讨论了这种情况．因此只考虑非幂零且不可逆的情况，总有式（4）～（6）满足1≤t＜s且1≤ind A．

文［15－16］继承了文［13－14］严谨准确的优点，但宋小力［12］认为此时涉及Jordan标准形等计算是复杂的，实际使用不方便．为此 ［12］删除了对（u，v）幂等矩阵u最小性的限制．

众所周知，Jor dan标准形是矩阵理论及应用的有效工具．Horn和Johnson指出：“虽然推导Jordan标准形的过程是一个明确的算法，它在原则上可以用来计算一个已知矩阵的Jor dan标准形，但是绝对不能指望用计算机对它自动实施数值计算．实际上并没有一个计算Jor dan标准形的数值方法．”［20］

本文证明了（u，v）幂等矩阵与本质（m，l）幂等矩阵的互相确定关系．由此不依赖通常的Jor dan标准形的算法，只应用矩阵方幂的秩和u－v次单位根εi所确定的矩阵秩，完全准确地给出（u，v）幂等矩阵的Jor dan标准形；进而得到了以矩阵秩为基本工具的判定（u1，v1）幂等矩阵与（u2，v2）幂等矩阵相似的充分必要条件．

1 预备知识

引理1［21］设A ∈Cn×n，则

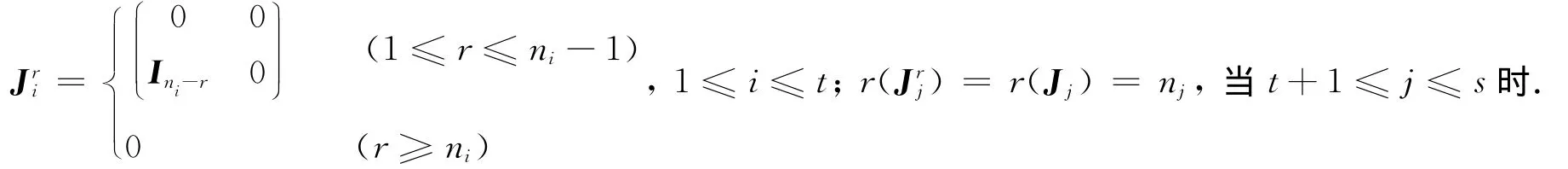
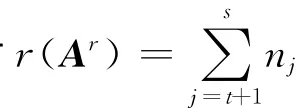
引理3 设A∈Cn×n，则ind A≥1⇔存在正整数l使得r（Al－1）＞r（Al），并且对任何r≥l，均有r（Ar）＝r（Al）．

证明 由矩阵指数的定义知必要性成立．

充分性：如果存在正整数l使得r（Al－1）＞r（Al），并且对任何r≥l，均有r（Ar）＝r（Al）．那么，显然有ind A＝l≥1．证毕．

引理2说明矩阵指数是其Jordan标准形中幂零Jordan块的最大阶数（由此可得文［21］的幂零矩阵结论）．

引理4 设A∈Cn×n所有不同特征值为μ1，μ2，…，μk，dj是μj的重数而pj是μj确定的Jordan块的个数，则r（A－μjIn）＝n－pj，j＝1，2，…，k．

证明 从已知可设A的Jor dan标准形

从式（7）、（8）知，r （J（μi－μj） ）＝r （J（μi）－μjIdi）＝di，当i≠j时；且由引理1得

当a∈C不为A∈Cn×n的特征值即r（A－a In）＝n时，约定由a∈C所确定的JA中Jor dan块的个数p＝0，于是由引理4可得．

引理5 设A∈Cn×n，a∈C，则a为A的特征值⇔r（A－a In）＜n；a不为A的特征值⇔r（A－a In）＝n；由a所确定的JA中Jor dan块的个数p＝n－r（A－a In）．

引理6［20］设A∈Cn×n所有不同特征值为μ1，μ2，…，μk，则mA（x）＝ （x－μi）ri，其中ri为特征值μi确定的JA中Jor dan块的最高阶数．

2 主要结论

定理1 设A ∈ EPn（m，l）（C），u，v∈N且u＞v．则A∈Pn（u，v）（C）⇔v≥l，且存在d∈N使得u＝d（m－l）＋v．

证明 必要性：由xv（xu－v－1）是A∈Pn（u，v）（C）的化零多项式，知A的非零特征值λ满足λu－v＝1且mA（x）整除xv（xu－v－1）．这样由A∈EPn（m，l）（C），由命题3和引理6得v≥l；再从命题3知A的所有非零特征值的阶的最小公倍数为m－l，因此存在（1≤）d∈N使得u－v＝d（m－l）即u＝d（m－l）＋v．

充分性：由v≥l，可设v＝l＋r，r∈N．从A∈EPn（m，l）（C）知Am－lAl＝Al．

对d作归纳法，当d＝1时，u＝（m－l）＋l＋r＝m＋r，此时Au＝Am＋r＝AlAr＝Av，结论成立．

假设对d－1成立，则有Au＝A（d－1）（m－l）＋v＝Av．对d，有Au＝A（d－1）（m－l）＋（m－l）＋v＝A（d－1）（m－l）＋vAm－l＝Al＋rAm－l＝ （Am－lAl）Ar＝Al＋r＝Av．证毕．

例2 设A＝diag（N4，I2，－I3），从A6＝A4＝diag（0，I2，I3）和命题3知A ∈EP9（6，4）（C）．当v＝132，d＝50时，由定理1知u＝232即A∈P9（232，132）（C）；这样由命题2得的JA中幂零Jor dan块的最大阶数≤v＝132．这对9×9矩阵没有任何实际意义．

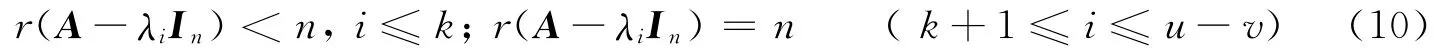
证明 从xv（xu－v－1）为A的化零多项式，知ε0，ε1，…，εu－v－1是A的所有可能两两不同非零特征值，由mA（x）整除xv（xu－v－1）和引理6知A的每个非零特征值确定的Jor dan块都是1阶的；由存在1≤l≤r∈N 使r（Al－1）＞r（Al）＝r（Ar）和引理3知ind A＝l．

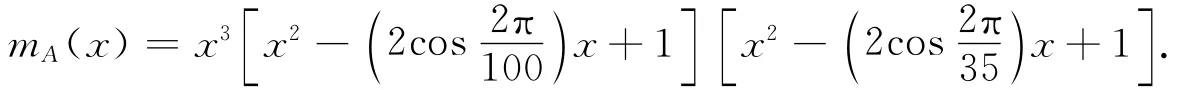
例3不仅说明应用（2）来判定A∈Pn（u，v）（C）计算量可能很大，而且知对给定的任意大的正整数m总存在A∈EPn（m，l）（C）．当A∈ （C）n×n且ind A＝l时，从引理2知式（4）～（6）中的幂零Jor dan块的不同阶数最多有l＝n1＝ind A个，这样可设

式（11）中的tl，…，t2，t1为JA中幂零Jor dan块的不同阶数的个数，ti∈N，i＝1，2，…，l．

定理3 设A∈EP（m，l）n（C），则

证明 由命题3和约定知1≤l＝ind A＝n1，1≤t；这样当1≤r≤l时，由式（11），引理1和引理2知：

即

由式（13）得

由和式（13）得，

可见式（14）对r＝1也成立，即

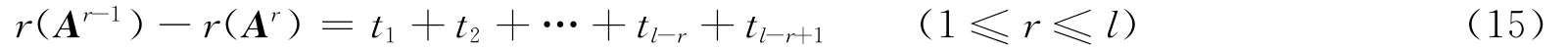
令l－r＋1＝f，则r＝l－f＋1，进而可得式（15）的等价形式

由式（16）得，tr＝ （t1＋t2＋ … ＋tr－1＋tr）－ （t1＋t2＋ … ＋tr－1）＝ （r（Al－r）－r（Al－r＋1））－ （r（Al－r＋1）－r（Al－r＋2）），即式（12）成立．证毕．

定理4 设A∈Pn（u，v）（C），r（Al－1）＞r（Al）并且对于任意r≥l，均有r（Ar）＝r（Al）．则必存在正整数k使式（9）、（10）成立且m＝［λ1，λ2，…，λk］＋l，此时A的Jor dan标准形为

式（18）中的J（0，r）∈Cr×r表示由特征值0确定的Jor dan块，tr由（12）确定．

证明：从定理1及其证明知ind A＝l且存在正整数k使式（9）、（10）成立且m－l＝［，，…，］，λ1，λ2，…，λk为A的所有非零特征值即A∈EPn（m，l）（C）．从命题3知，由λi确定的Jor dan块都是1阶的，再由引理4得λi的重数ni＝n－r（A－λiIn），因此JA＝diag（M，λ1In1，λ2In2，…，λkInk），其中M是由A的所有幂零的Jor dan块构成的．这样从式（12）知式（18）成立，进而可得式（17）．证毕．

从命题2不能准确给出A∈Pn（u，v）（C）的JA．我们不依赖通常的Jor dan标准形算法，可给出由（17）～（18）确定的JA．由定理1知（u，v）有很多种命名，因此不容易确定这类矩阵的相似关系．

定理5 设A∈Pn（u1，v1）（C），B∈Pn（u2，v2）（C），r（Al－1）＞r（Al）并且对于任意r≥l，均有r（Ar）＝r（Al）．如果u－v＝ ［u1－v1，u2－v2］且u＞v≥ max｛v1，v2｝，则

A与B 相似 ⇔r（Ar）＝r（Br），1≤r≤l；r（A－εiIn）＝r（B－εiIn），0≤i≤u－v－1．

证明 必要性是显然的．只证明充分性．从存在1≤l≤r∈N使r（Al－1）＞r（Al）＝r（Ar）和定理2知ind A＝l；由r（Ar）＝r（Br），1≤r≤l和引理3知ind A＝ind B＝l．由u－v＝［u1－v1，u2－v2］且u＞v≥max｛v1，v2｝知，存在f1，f2∈N使得u－v＝f1（u1－v1）＝f2（u2－v2），从u＞v知1≤f1∈N．

对（1≤）f1∈N用归纳法证明，Au＝Av；此时可设v＝v1＋r1，r1∈N．

当1＝f1即u＝（u1－v1）＋v1＋r1＝u1＋r1时，Au＝Au1 Ar1＝Av1 Ar1＝Av，即结论成立．

假设f1－1时，Au＝A（f 1－1）（u1－v1）＋v＝Av．这样当u＝ （f1－1）（u1－v1）＋v＋ （u1－v1）时，Au＝A（f 1－1）（u1－v 1）＋vAu1－v1＝AvAu1－v1＝Au1－v 1＋v1＋r 1＝Au1Ar 1＝Av1Ar 1＝Av 1＋r 1＝Av．

类似可证明当u－v＝f2（u2－v2）时，总有Bu＝Bv．这样可知A，B∈Pn（u，v）（C），因此ε0，ε1，…，εu－v－1是A，B的所有可能的非零特征值．由r（A－εiIn）＝r（B－εiIn），i＝0，1，2，…，u－v－1和引理4、5知存在正整数k使式（9）、（10）对A、B同时成立；因为ind A＝ind B＝l，所以m＝［，，…，］＋l，进而由定理2知A、B∈EPn（m，l）（C），同时λ1，λ2，…，λk为A、B的所有非零特征值且相应重数相同；这样再由r（Ar）＝r（Br），1≤r≤l；应用式（12）、（17）、（18）知JA＝JB即A、B相似．证毕．

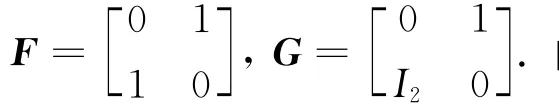
例4说明即使有相同的最小多项式的A，B∈EPn（m，l）（C）也未必总是相似的．

推论1 设A∈Pn（u1，v1）（C），B∈Pn（u2，v2）（C）且mA（x）＝mB（x）；如果u－v＝ ［u1－v1，u2－v2］且u＞v≥max｛v1，v2｝；则A与B相似 ⇔r（Ar）＝r（Br），1≤r≤n；r（A－εiIn）＝r（B－εiIn），i＝0，1，…，u－v－1．

证明 将引理2和引理6应用到mA（x）＝mB（x），就知ind A＝ind B＝l，这样从定理5知推论1成立．证毕．

由定理4和定理5可得文［23］幂零矩阵的Jor dan标准形的相应结果，当然文［1－7］和文［19］等涉及的m幂等、m幂幺矩阵的结论可在当v＝1，v＝0时给出．

［1］Baksalary O M，Trenkler G．On k－potent matrices［J］．Electronic Journal of Linear Algebra，2013，26：446－470．

［2］Mc Closkey J P．Characterizations of r－potent matrices［J］．Mathematical Proceedings of t he Cambridge Philosophical Society，1984，96：213－222．

［3］Chen Meixiang，Yang Zhongpeng，Feng Xiaoxia．Invariance of rank and nullity for the linear co mbination of m（≥3）－scalar－idempotent matrices［J］．International Journal of Applied Mathematics and Statistics，2011，21（11）：141－147．

［4］Ye Suhua，Chen Yizhi，Luo Hui．On generalized m－power matrices and tansfor mations［J］．International Journal of Mathematical Co mbinatorics，2012（2）：71－75．

［5］唐建国，严青云．幂幺矩阵的充要条件［J］．数学的实践与认识，2010，40（20）：172－176．

［6］陈益智．m次幂等矩阵的等价条件［J］．数学的实践与认识，2011，41（23）：190－193．

［7］杨忠鹏，林志兴．矩阵方幂的秩的一个恒等式及应用［J］．北华大学学报：自然科学版，2007，8（4）：294－298．

［8］杨忠鹏，陈梅香，林国钦．关于矩阵方幂的秩恒等式的注记［J］．福州大学学报：自然科学版，2009，37（1）：24－28．

［9］吕洪斌，杨忠鹏，冯晓霞，等．广义m对合矩阵和（m，l）幂等矩阵的充要条件及应用［J］．吉林大学学报：理学版，2012，50（6）：1 069－1 074．

［10］史及民．关于Schur补应用的一点注记［J］．应用数学学报，2002，25（2）：318－321．

［11］Styan G P H．Notes on the distribution of quadratic for ms in singular nor mal variates［J］．Bio metrika，1970，57：567－572．

［12］宋小力．关于（m，l）幂等矩阵的充要条件［J］．曲阜师范大学学报：自然科学版，2012，38（2）：37－40．

［13］Baksalar y J K，Backsalar y O M，Styan G P H．Idempotency of linear combinations of an idempotent matrix and tripotent matrix［J］．Linear Algebra and its Applications，2002，304：21－24．

［14］Ozdemir H，Sar duvan M，Ozban A Y，et al．On idempotency and tripotentcy of linear co mbinations of t wo co mmuting tripotent matrix［J］．Applied Mathematics and Co mputation，2009，207（1）：197－201．

［15］杨忠鹏，陈梅香，郭文静．本质（m，l）幂等矩阵的特征研究［J］．数学研究，2011，44（1）：86－94．

［16］Chen Meixiang，Lyu Hongbin，Feng Xiaoxia，et al．The essential（m，l）idempotent matrix and its mini mal polynomial［J］．Inter national Jour nal of Applied Mathematics and Statistics，2013，41（11）：31－41．

［17］Ber nstein D S．Matrix mathematics theor y，facts，and f or mulas［M］．2th ed．Princeton：Princeton University Press，2009．

［18］Nikuie M，Mirnia M K，Mahmoudi Y．Some results about the index of matrix and drazin inverse［J］．Mathematical Sciences，2010，4（3）：283－294．

［19］林大华，戴立辉．幂幺矩阵的幂幺指数［J］．数学的实践与认识，2012，42（18）：252－255．

［20］Hor n R A，Johnson C R．Matrix analysis［M］．New Yor k：Cambridge University Press，1985．

［21］Wu Yan，Linder D F．On the eigenstr uct ures of f unctional k－potent matrices and their integral for ms［J］．WSEAS Transactions on Mathematics，2010，4（9）：244－253．

［22］Gau H L，Wang C J，Wong N C．Invertibility and Fredhol mness of linear combinations of quadratic，k－potent and nilpotent operators［J］．Operators and Matrices，2008，2（2）：193－199．

［23］吕洪斌，杨忠鹏，冯晓霞，等．矩阵的秩与非零特征值个数差的确定［J］．吉林大学学报：理学版，2014，52（6）：1 210－1 214．