嫦娥3号软着陆轨道设计

袁训锋，李磊, 魏蕾

（商洛学院电子信息与电气工程学院,陕西商洛726000）

嫦娥3号软着陆轨道设计

袁训锋，李磊, 魏蕾

（商洛学院电子信息与电气工程学院,陕西商洛726000）

软着陆轨道设计是月球探测中的关键技术之一。基于2014高教社杯全国大学生数学建模竞赛A题，针对嫦娥3号软着陆轨道设计问题，运用开普勒定律和能量守恒定律准确获得近月点、远月点的位置和速度；根据软着陆的动力学方程，以消耗燃料量为最优化条件，利用Matlab对嫦娥3号的最优软着陆轨道进行仿真。结果表明，设计的最优轨道较好满足所要求的约束条件，能够为探测器软着陆轨道设计提供一定参考。

软着陆；轨道设计；能量守恒

随着现代航天科技的发展，月球探测研究不断深入，众多学者针对月球探测器着陆问题进行了大量的科学研究。林胜勇等[1]采用月球垂直着陆的数学模型仿真了不同推力条件下的着陆轨道运动特性。和兴锁等[2]在分析有限推力最省燃料直接软着陆轨道结果的基础上，获得开始制动高度越低越省能量的结论。王明光等[3]在优化软着陆轨道算法的基础上，使用伪光谱方法进行问题转化，乘子法处理约束条件，变尺度法求解。单永正等[4]详细探讨了如何选择初始点和软着陆轨道。郭景录[5]、曹涛[6]分别采用蛙跳算法和组合优化策略，对登月软着陆轨道进行了优化设计。罗宗富等[7]应用进化策略对月球的软着陆探测器轨道进行了设计，采用STK仿真验证了设计思路的有效性。

我国的月球探测计划“嫦娥工程”已经顺利开展，嫦娥3号是中国国家航天局嫦娥工程第二阶段的登月探测器。蒋瑞等[8]针对嫦娥3号着陆控制方案建立数学模型，并使用Simulink软件进行仿真，获得满意的仿真结果，从而为嫦娥3号着陆控制方案的最终确定提供依据。嫦娥3号于2013年12月2日成功发射，12月6日顺利抵达月球轨道，但是嫦娥3号的实际软着陆过程与预先设计的最优着陆轨道并不完全相同，该问题的核心是软着陆轨道的设计与控制策略。在2014年高教社杯全国大学生数学建模竞赛中，将“嫦娥三号软着陆轨道设计与控制策略”作为A题，引起众多学者的关注。杜剑平等[9]将软着陆的优化设计问题转化为主发动机推力的泛函极值问题，通过求解计算获得各阶段的最优控制函数和控制策略。冷建华[10]利用开普勒定律和能量守恒定律分析获得嫦娥3号着陆准备轨道的近月点、远月点的位置及速度。何悠等[11]采用函数逼近法确定嫦娥3号的软着陆轨迹，运用Matlab图像处理和改进的局部最优算法确定降落区域，获得燃料消耗最少的控制策略。李祥宇[12]、刘林林[13]对嫦娥3号探测器推动力和着陆控制过程进行敏感性分析。

基于2014高教社杯全国大学生数学建模竞赛A题，针对嫦娥3号软着陆轨道设计问题，运用开普勒定律和能量守恒定律计算近月点、远月点的位置和速度；根据软着陆的动力学方程，以消耗燃料量为最优化条件，利用Matlab仿真其软着陆轨道。

1 近月点与远月点速度确定

嫦娥3号在准备软着陆时，首先从圆形轨道变轨，进入一条远月点高度约为100 km，近月点高度约为15 km的椭圆形轨道。当到达近月点时，制动发动机点火，嫦娥3号进入减速下降段。当嫦娥3号在椭圆形轨道运行时，可以把嫦娥3号看做质点来研究，即可以利用开普勒行星运动第二定律来求解嫦娥3号所在轨道参数及着陆初始值。

嫦娥3号椭圆轨道如图1所示。根据开普勒第二定律，设轨道周期为T，嫦娥3号到月球的半径在每秒种扫过相等面积S1=abπ/T。近月点距离：h=15 km，远月点距离：H=100 km，月球平均半径：R=1737.013 km，椭圆长半轴：a=(h+H+2R)/2= 1794.513 km，椭圆半焦距：c=a-h-R=42.5 km，椭圆短半轴：b=(a2-c2)1/2=1794.010 km。

图1 椭圆轨道模型

嫦娥3号在近月点速度达到最大Vmax=lh，在远月点速度达到最小Vmin=lH。近似化处理过程如图2所示。易知S1=0.5(R+h)lh，嫦娥3号在近月点的相对速度为1.7 km·s-1，则：

故在近月点的速度为1.7 km·s-1。方向为此点的切线方向。在远月点的速度为1.62 km·s-1，方向为此点的切线方向。

图2 近月点和远月点速度近似化过程

2 近月点与远月点位置的确定

嫦娥3号将在近月点15 km处以抛物线下降，相对月球速度每秒1.7 km逐渐降为零。下降过程中在竖直方向分量的反推力克服月球重力做功，使得着陆时竖直方向速度为零，即能量守恒Mg0=Fnh。下降过程中在水平方向分量的反推力做功，使得着陆过程中水平速度从1.7 km·s－1变为零，即能量守恒0.5MV2max= FτS。从而求解出嫦娥3号从近月点到达着陆点时的水平位移，进而推算出近月点位置与远月点位置。

嫦娥3号软着陆过程简化如图3所示。由Mg0h=Fnh得：Fn≈4 000 N,即嫦娥3号在下降过程中受到的反推力在竖直方向上的平均分量为4 000 N。由于安装在嫦娥3号下部的主减速发动机能够产生1 500 N到7 500 N的可调节推力，经过粗略计算分析，选取6 000 N作为嫦娥三号在下降过程中受到的反推力在水平方向上的平均分量，即Fτ=6 000 N。由能量守恒得0.5MV2max=FτS。解得：S≈578 km，即ob段为578 km。(在此求解过程中忽略bc段对下降高度及水平位移的影响,由于采用能量守恒求解，所以结果不受软着陆轨道形状的影响，即不考虑ab段形状的影响)。

假设嫦娥3号轨道倾角为30°，运行方向自西向东，经纬度分析如图4所示。

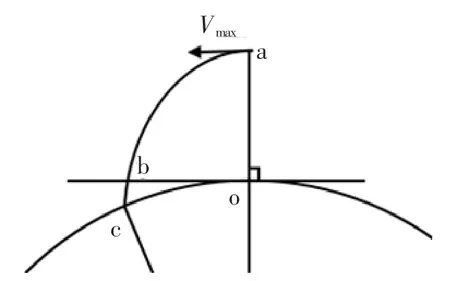
图3 嫦娥3号软着陆过程简化

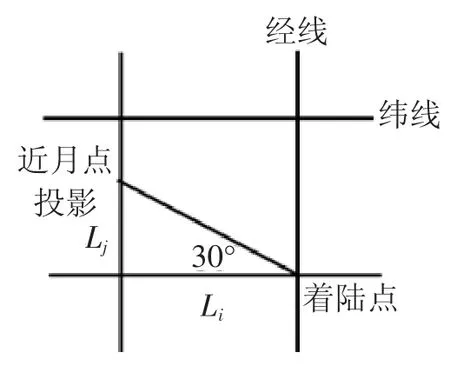
图4 经纬度分析

由图4解得：

所以近月点所在经度为19.51+16.51=36.02°W，近月点所在纬度为44.12+9.53=53.65°N，高度为15 km，与之对应的远月点的经纬度为180-36.02= 143.98°E,53.65°S,高度为100 km。

3 最优定点着陆问题描述

无量纲化后的软着陆动力学方程[14-15]为：

嫦娥3号的初始条件，位置约束：θ(τ0)=θ0，φ(τ0)=φ0，r(τ0)=RL+h0;速度约束：u(τ0)=0，v(τ0)=v0，w(τ0)=0。嫦娥3号的终端条件，位置约束：θ(τf)=θf，φ(τf)=φf，r(τf)=RL+hf；速度约束：u(τf)=0，v(τf)=0，w(τf)=0。推力方向角应满足：α∈[αmin,αmax],β∈[βmin,βmax]；着陆的过程中法向和侧向速度应满足：u∈[umin,umax],ω∈[ωmin,ωmax];飞行器着陆过程所消耗的燃料mu应满足：mu≤mmax，性能指标函数应选取燃料最省，即：

本文中取推力大小为常值，因此性能指标函数等价于着陆时间最短，即：

直接利用初始位置参数和着陆过程状态要求作为上述方法的初始值和约束条件。

4 仿真求解最优着陆轨道

动力下降初始及终端条件为：h0=15 km，θ0=36.02°，φ0=53.65°，u0=0，ν0=1.7 km·s-1，ω0=0；hf=-2.641 km，θf=19.5°，φf=44.12°，uf=0，νf=0，ωf=0。月球引力常数μ=4902.802 km3·s-2，自转角速度ω=2.6617×10-6rad·s－1，月球半径RL=1737.013 km，着陆器初始质量m0=2.4×103kg，初始轨道倾角i0=30°，制动发动机推力T=6 000 N，比冲Isp=2940 m·s－1。求解过程中约束推力方向角α∈[-50°,40°], β∈[130°,220°]，法向和侧向速度的取值范围为[-110,110]m·s－1，着陆过程燃料消耗mu≤300 kg。代入初始参数，通过Matlab仿真得到不同视角下最优着陆轨道如图5所示。从仿真结果可以看出，最优软着陆轨道具有良好的光滑性，即在实际工程当中具较高的可实现性与可操作性。

5 结论

针对嫦娥3号软着陆轨道设计问题，运用开普勒定律求得在近月点的速度为1.7 km·s-1，方向为此点的切线方向；在远月点的速度为1.62 km·s-1，方向为此点的切线方向。采用能量守恒定律计算获得近月点所在经度为19.51+16.51=36.02°W，近月点所在纬度为44.12+9.53=53.65°N,高度为15 km；与之对应的远月点的经纬度为180-36.02=143.98°E,53.65°S,高度为100 km。利用Matlab对嫦娥3号的最优软着陆轨道进行仿真，结果表明设计的最优轨道较好满足所要求的约束条件，能够为探测器软着陆轨道设计提供一定参考。

图5 不同视角下最优着陆轨道

[1]林胜勇,李珠基,和兴锁.月球垂直软着陆轨道初步设计[J].中国空间科学技术,2005(2)：47-51.

[2]林胜勇,李珠基,和兴锁.月球探测器直接软着陆最优轨道设计[J].宇航学报,2007,28(2)：409-413.

[3]王明光,裴听国,袁建平.基于伪光谱方法月球软着陆轨道快速优化设计[J].中国空间科学与技术,2007(5)：27-32.

[4]单永正,段广仁,张烽.月球精确定点软着陆轨道设计及初始点选取[J].宇通学报,2009,30(6)：2099-2104.

[5]郭景录,付平.登月着陆轨道优化算法研究[J].计算机仿真,2009,26(12)：70-73.

[6]曹涛,董长虹.基于组合优化策略的月球软着陆最优轨道设计[J].北京航空航天大学学报,2012,38(11)：1537-1541.

[7]罗宗富,孟云鹤,汤国建.基于进化策略的月球软着落探测轨道设计[J].空间科学学报,2012,32(1)：92-98.

[8]蒋瑞,韩兵.嫦娥三号着陆控制研究与软件仿真[J].微型电脑应用,2012,28(2)：17-19.

[9]杜剑平,韩中庚.嫦娥三号软着陆轨道设计与控制策略的优化模型[J].数学建模及其应用,2014,3(4)：39-53.

[10]冷建华.嫦娥三号软着陆轨道设计[J].山东工业技术, 2014,32(24)：3-4.

[11]何悠,罗琦,刘金华.嫦娥三号软着陆轨道设计与控制策略[J].硅谷,2014,13(23)：14-15.

[12]李祥宇,宋艺旋,吕晨,等.嫦娥三号软着陆轨道设计与控制策略[J].佳木斯大学学报,2015,33(1)：123-127.

[13]刘林林,刘裴倩,杨青,等.嫦娥三号软着陆轨道设计与控制策略[J].运城学院学报,2014,32(5)：27-30.

[14]彭祺擘,李海阳,沈红新,等.基于Gauss伪谱法和直接打靶法结合的月球定点着陆轨道优化[J].国防科技大学学报,2014,34(2)：120-123.

[15]雍恩米,唐国金,陈磊.基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J].宇航学报,2008,29 (6)：1766-1772.

（责任编辑：李堆淑）

Design of Chang'e-3 Soft Landing Orbit

YUAN Xun-feng,LI Lei,WEI Lei
（CollegeofElectronicInformationandElectricalEngineering,ShangluoUniversity,Shangluo726000,Shaanxi）

The soft landing orbital design is one of the key technologies in lunar exploration.Based on Problem A of Contemporary Undergraduate Mathematical Contest in Modeling 2014 for college students, for the Chang'e-3 soft landing orbital design's problem,using the Kepler's law and velocity of perilune and apolune,with the kinetic equation of soft landing,and the amount of fuel consumption as the optimization conditions,Matlab to Chang'e-3 optimization soft landing orbit is utilized to proceed simulation.The results show that the optimization orbit of the design can better meet the requivement of the constraint equation.It will bring about reference for the exploration of soft landing orbit.

soft landing;orbital design;energy conservation

V412.41

A

1674-0033（2015）02-0024-04

10.13440/j.slxy.1674-0033.2015.02.007

2014-12-18

陕西省教育科学“十二五”规划资助项目（SGH13401）

袁训锋，男，湖北神农架人，博士，讲师