离散正系统的静态输出反馈控制

黄丽琼

（商洛学院数学与计算机应用学院，陕西商洛726000）

离散正系统的静态输出反馈控制

黄丽琼

（商洛学院数学与计算机应用学院，陕西商洛726000）

通过分析标准离散时间正系统的稳定性条件，利用矩阵的奇异值分解方法，以线性规划的形式给出单输出离散时间正系统渐进稳定和鲁棒稳定的三个充分必要条件。其次，通过构造一个静态输出反馈控制器，给出多输出离散正系统稳定的一个充分必要条件。

正离散系统；稳定性；静态输出反馈

正系统是指系统从一个非负初始状态出发，系统的状态都保持在一个正象限中，这类系统几乎出现在所有的领域中，例如：生物系统，人口系统，经济系统，社会科学系统等，由于正系统的状态变量是定义在一个锥上而不是像其他系统的状态变量定义在一个线性空间上，所以正系统的研究更具有复杂性，文献[1-2]给出了正系统的正性刻画条件，文献[3-4]给出了离散正系统稳定的充要条件，文献[5-6]给出了离散正时滞系统稳定的充要条件，文献[7]给出了含有动态输出反馈控制的正系统稳定的充要条件，文献[8]利用线性矩阵不等式及矩阵等式给出了含静态或动态输出系统的反馈控制器存在的充要条件，文献[9]利用线性规划(LP)方法给出了单输入单输出正离散线性系统稳定的充要条件，文献[10]利用线性规划的方法给出了连续正线性系统存在静态输出反馈控制器使得闭环系统是正的且是渐进稳定的充要条件。本文主要利用奇异值分解法，以线性规划的形式讨论离散正线性系统的静态输出反馈控制问题。

1 定义与引理

考虑离散时间系统(1)

其中x(t)是变量，A是不变矩阵。

定义1[2]如果对每一个可容许初始状态x(0)≥0，系统(1)的状态轨迹都是非负的，即x(k)≥0，(k∈N)，则称系统(1)是正(非负)系统。

引理1[8]线性系统(1)是正(非负)的，当且仅当A∈Rn×n是正(非负)的。

定义2[2]矩阵A∈Rn×n是正的，当且仅当A∈Rn×n的所有元素都是正的。

引理2[8]线性系统(1)是渐进稳定的，当且仅当A∈Rn×n是渐进稳定的。

引理3[9]线性系统(1)是正的且是渐进稳定的，当且仅当存在一个λ∈R+n，使得(A-I)λ＜0。

引理4[9]矩阵A-，A+为给定的方阵，在区间A-≤A≤A+上的所有矩阵是非负的且是渐进稳定的，当且仅当A-是非负的，A+是渐进稳定的。

2 定理及其证明

2.1 单输出情况

考虑系统(2)

其中x(k)∈Rn是状态变量，u(k)∈Rr是输入变量，y(k)∈R是测量输出，A∈Rn×n，B∈Rn×r，C∈R1×n≥0为不变矩阵。

假设系统(2)存在一个静态输出反馈控制器(3)

则得到闭环系统(4)

其中K∈Rr×1是反馈增益矩阵。

定理1系统(2)中的矩阵C可分解为CVT= [σ，0，…，0]，其中σ为C的奇异值，V为正交矩阵，那么存在一个静态输出反馈控制器(3)使得闭环系统(4)是正的且是渐进稳定的，当且仅当存在向量p=[p1，p2，…，pn]T和z∈Rr×1使得

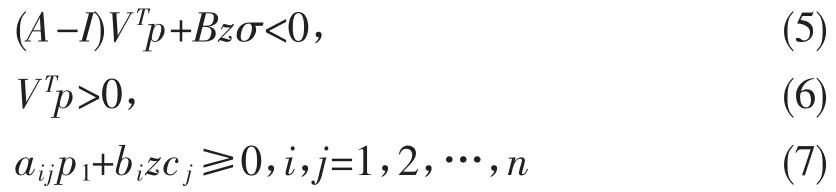
成立，其中A=[aij]，BT=[b1T，b2T，…，bnT]T，C=[c1，c2，…，cn]，增益矩阵K为

证明必要性：假设存在静态输出反馈(3)使得闭环系统(4)是正的且是稳定的，由引理2可得存在一个λ＞0使得

(A+BKC-I)λ＜0，

设λ=VTp＞0，其中V是正交矩阵，则p=Vλ= [p1，p2，…，pn]T，又因C=[σ，0，…，0]V，z=p1K，则

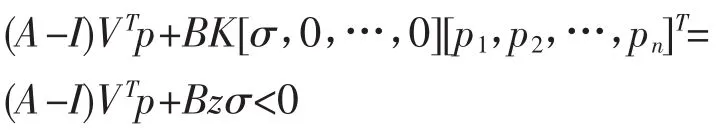
又由引理1可得A+BKC≥0，即aij+biKcj≥0，设V=[v1，v2，…，vn]T，由p=Vλ及CVT=[σ，0，…，0]，得λ，又因C＞0，σ＞0，λ＞0，则得p1＞0，对aij+biKcj≥0左右两端同乘p1，得aijp1+bizcj≥0，i，j=1，2…，n。

充分性：假设存在向量p=[p1，p2，…，pn]T∈Rn×1和z∈Rr×1使得(5)-(7)成立，由K=p1-1z，得z=p1K，从必要性的证明中得知p1＞0，由(7)式得aijp1+bizcj=(aijbiKcj)p1≥0，i，j=1，2…，n因此得A+BKC是非负矩阵，则闭环系统(4)是正系统。又因

则闭环系统(4)是稳定的。

定理2假设系统(2)对矩阵C存在定理1中的奇异值分解，设A=[aij]，BT=[b1T，b2T，…，bnT]T，C=[c1，c2…，cn]，则存在一个静态输出反馈控制器(3)使得闭环系统(4)是正的且是稳定的，当且仅当存在向量p=[p1，p2，…，pn]T∈Rn×1和z∈Rr×1使得(9)式的两个LP问题至少有一个成立。

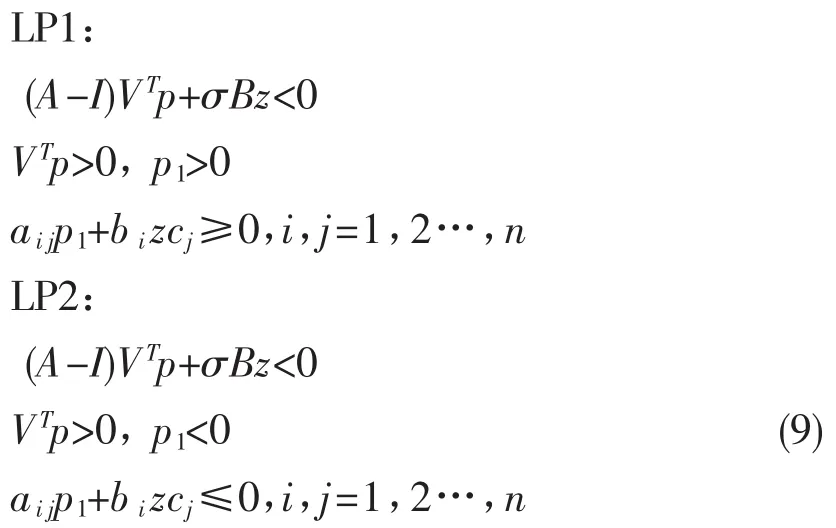
增益矩阵K有参数形式K=p1-1z。

2.2 鲁棒稳定

考虑区间正离散系统(10)

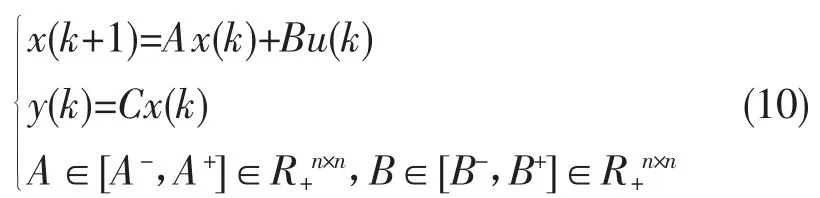
其中A-，A+，B-，B+是未知非负矩阵，C≥0。

定理3假设系统(10)对矩阵C≥0存在定理1中的奇异值分解，定义A-=[aij-]，[B-]T=[(b1-)T，(b2-)T]，…，(bn-)T，C=[c1，c2，…，cn]，则存在静态输出反馈控制器(3)使得闭环系统是正的且是鲁棒稳定的，当且仅当存在向量p=[p1，p2，…，pn]T∈Rn×1和z∈Rr×1满足

增益矩阵K有参数形式K=-p1-1z。

证明必要性：假设存在矩阵K=-p1-1z＜0使得闭环系统对于任意非负矩阵A，B是正的且是鲁棒稳定的，则知A+BKC是正的，又因A∈[A-，A+]，B∈[B-，B+]，取A=A-，B=B+有A-+B+KC是正的，由定理1必要性证明知p1＞0，可得aij-p1-bi+zcj≥0，又因(A+BKC-I)λ＜0取λ=VTp，得(A+-I)VTp-B-σz＜0。

充分性：由于A∈[A-，A+]，B∈[B-，B+]由定理1的必要条件知p1＞0，则K＜0得

由于aij-p1-bi+zcj=aij-p1+bi+p1Kcj=(aij-+bi+Kcj)p1≥0，则知A-+B+KC≥0，由引理4知A+BKC≥0，则知闭环系统是正的。设λ=VTp，又由于

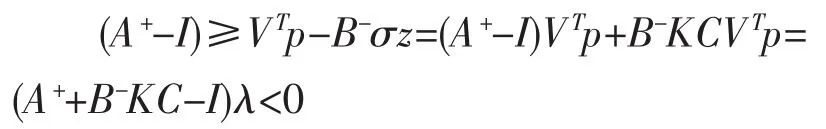
由引理4知(A+BKC-I)λ＜0，即闭环系统是渐进稳定的。

2.3 多输出情况

考虑多输出系统(11)

定理4假设存在固定参数v使得vC＞0，对vC进行奇异值分解vCVT=[σ，0，…，0]，其中σ＞0是vC的奇异值，V为正交矩阵，则存在静态输出反馈控制器u(k)=Kvy(k)使得闭环系统是正的且是渐进稳定的，当且仅当存在向量p=[p1，p2，…，pn]T∈Rr×1及z∈Rr×1使得LP问题(12)成立：

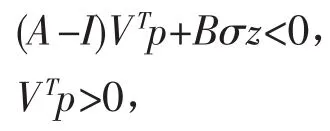
其中增益矩阵K为K=p1-1z。

[1]Farina L,Rinaldi S.Positive linear systems theory and applications[M].John Wiley and Sons,New York, 2000：165-221.

[2]Rumchev V G,Caccetta L,Kostova S.Positivelinear dynamic model of mobile source of pollution and problems of control[M].Coventry University Coventry, 2003：602-607.

[3]James G.Stability of linear discrete-time systems[J].Technical Sciences,2005,53(1)：1-8.

[4]Fornasini E,Valcher M E.Stability and stabilizability criteria for discrete-time positive switched systems[J].IEEE TransAciIons on Automatic Control,2011,57(5)：1208-1221.

[5]Liu X,Wang L,Zhong S.Constrained control of positive discrete-time systems with delays[J].Transition on Circuits and Systems-II,2008,55(1)：193-197.

[6]黄丽琼.离散正奇异切换系统的稳定性[J].商洛学院学报,2014,28(6)：16-18.

[7]Shu Z,Lam J.Positive observers and dynamic outputfeedback controlles for interval positive linear systems [J].IEEE Transactions Circuits System,2008,55(10)：3209-3222.

[8]Feng J,Lam J.Declay rate constrained stabilization of positive systems using static output feedback[J].International Journal of Rubust and Nonlinear Control, 2011,21(1)：44-54.

[9]Rami M A.Solvability of static output-feedback stabilization for LIM positive systems[J].Systems and Control,2011(60)：704-708.

[10]Meng M,Zhu S Q,Zhang C H.Static output feedback sontrol for positive systems via LP approach[C].The 31th Chinese Control Conference,2012：25-27.

（责任编辑：李堆淑）

Static Output Feedback Control for Discrete-time Positive Systems

HUANG Li-qiong
（College of Mathematics and Computer Application,Shangluo University,Shangluo726000,Shaanxi）

Through analysis of the stability conditions of the positive standard discrete-time system,by using the singular value decomposition approach,necessary and sufficient conditions for the stability, robust stability are established in term of standard linear programming problems(LP).Specifilly,through constructing the static output feedback controler,necessary and sufficient condition for the stability of the multi-output discrete-time positive systems is given.

positive discrete-time system;stability;static output feedback

O231

A

1674-0033（2015）02-0009-03

10.13440/j.slxy.1674-0033.2015.02.003

2015-01-26

商洛学院科研基金项目(14SKY008)

黄丽琼，女，陕西洛南人，硕士，助教