一种基于思维进化算法的极限学习机及其应用

刘俊

（商洛学院电子信息与电气工程学院，陕西商洛726000）

一种基于思维进化算法的极限学习机及其应用

刘俊

（商洛学院电子信息与电气工程学院，陕西商洛726000）

极限学习机（Extreme Learning Machine,ELM）是一种新型的单隐含层前馈神经网络，与传统神经网络训练方法相比，ELM具有泛化能力好、学习速率快等优点。但随机产生的输入权值和阈值，往往会出现一些作用很小或“无用”的值，为了达到理想精度，通常需要增加隐含层节点数。思维进化极限学习机使用思维进化算法MEA优化输入权值矩阵和阈值向量，再利用MP广义逆求出输出权值矩阵，从而减小隐含层节点数，增大网络预测精度。通过函数拟合仿真实验，并同ELM算法和BP神经网络算法比较，思维进化极限学习机算法可以用较少的隐含层节点数实现更高的精度。

思维进化；极限学习机；权值；阈值

随着智能信息的发展，具有良好系统辨识能力的神经网络得到了更广泛的应用，但传统神经网络（如BP、SVM神经网络）的固有缺陷，如收敛速度慢、易收敛到局部最优解、过拟合问题、网络隐含层节点数多且不能确定等，成为制约其发展的主要瓶颈。极限学习机（Extreme Learning Machine,ELM）是黄广斌等[1]提出一种新的单隐层前馈神经网络（Single-hidden Layer Feedforward Neural Network,SLFN）。该算法随机选取输入层与隐含层间的连接权值和隐含层节点的阈值，且在训练过程中无需调整，只需设置隐含层节点数目，再通过一步计算得到方程组的最小二乘解，即隐含层与输出层的连接权值。因此，ELM较传统网络模型具有更快的学习速度、更高的精度和更强的泛化能力，已经得到很多学者的应用研究[2-5]。但实际应用中，为了达到较好精度，隐含层节点数目需不断增加，增大了网络复杂度。从理论上已经证明输入层与隐含层的连接权值和隐含层的阈值的选择对网络精度有较大影响[6]。思维进化算法（Mind Evolutionary Algorithm，简称MEA）是由孙承意等[7]提出的一种新型进化算法，其思想来源于模仿人类思维进化过程，较遗传算法（Genetic Algorithms,GA）具有更快的收敛时间和更强的全局搜索能力。MEA在进化过程中每一代所有个体（潜在解）组成一个群体，并形成若干个子群体，子群体又分成优胜子群体和临时子群体两类，每个子群体内部执行“趋同”操作，得到局部最优解，每个子群体之间执行“异化”操作，得到全局最优解。由于MEA具有良好的扩充性、移植性和极强的全局优化能力，已经成功应用于图像处理、自动控制、经济预测等领域[8-10]。针对ELM随机产生的输入权值和阈值有时会出现0值或作用很小的值，对网络精度和复杂度有较大影响，本文提出思维进化极限学习机算法（MEAELM），采用思维进化算法优化极限学习机的输入权值和隐含层阈值，再利用MP广义逆得到输出权值矩阵。通过函数拟合应用实验，并与ELM算法、BP神经网络算法作比较，验证了MEAELM可使用更少的隐含层节点数目获得更高的精度，同时具有更强的泛化能力。

1 极限学习机

1.1 ELM基本原理

ELM属于单隐含层前馈神经网络，设输入层有m个神经元，隐含层有l个神经元，输出层有n个神经元。g(·)为隐含层神经元的激活函数。输入权值矩阵为ωj=[w1,w2,…,wl]T，其中第j个隐含层神经元的权值向量ωj=[wj1,wj2,…，wjm]，wj1为隐含层第j个神经元与第i个输入神经元的连接权值。隐含层阈值向量b=[b1,b2,…,bl]T。设k个不同样本（Xk,Yk），其中输入矩阵Xk=[x1,x2,…,xk]，第j个样本输入向量xj=[x1j,x2j,…xmj]T，xij为第j个样本的第i个输入神经元输入量。输出矩阵Yk=[y1, y2,…,yk]，第j个样本输出向量yj=[y1j,y2j,…ynj]T，yij为第j个样本的第i个输出神经元输出量。隐含层与输出层连接权值矩阵β=[β1,β2,…,βl]T，其中第j个隐含层神经元与输出神经元连接权值向量βj=[βj1,βj2,…,βjn]，βjl表示第j个隐含层神经元与第i个输出层神经元的连接权值。

隐含层输出矩阵可以用上述假设参量表示为H=[h1,h2,…,hl]，其中第j个隐含层神经元的输出矩阵hj=[g(wj·x1+bj),g(wj·x2+bj),…,g(wj·xk+bj)T。

网络输出矩阵T=Hβ。ELM的输入权值和阈值可以随机选取，且在训练过程中保持不变，当激活函数g(·)无限可微时，通过解范数方程的最小二乘解获得隐含层与输出层的连接权值β^=H+T，H+为H的MP伪逆。根据文献[11]的定理证明，β^是惟一的，使得训练误差最小，且使网络有最好的泛化能力。

1.2 ELM学习步骤

ELM学习算法主要实现步骤：

1）确定隐含层节点的数目l和无限可微激活函数g(·)；

2）随机产生输入权值矩阵Wl和隐含层阈值向量b；

3）计算隐含层输出矩阵H；

4）计算输出权值矩阵β。

2 思维进化算法

思维进化算法（MEA）是在遗传算法的基础进行了改进。MEA具有更强整体搜索效率，可以记忆多代的进化信息，通过趋同和异化操作实现信息向着有利方向进行。

在解空间中随机生成Q个个体，根据得分（即适应度函数值）选择得分最高的前M个优胜个体和N个临时个体。分别以所有优胜个体和临时个体为中心，随机生成M个优胜子群体和N个临时子群体。子群体内部个体通过得分高低进行局部竞争，若胜者（即最高分个体）不再发生变化，表示该子群体成熟，此过程为趋同操作。直到所有子群体全部成熟，并把各子群体最高得分及其个体公布到全局公告板上。根据全局公告板信息，子群体间为优胜者而进行全局竞争，完成子群体间的替换、废弃、个体释放等操作，此过程为异化操作，最后得到全局最优个体和得分。若最优个体没有满足要求，可以重复趋同和异化操作，直到运算收敛或满足设定要求。

3 思维进化极限学习机

实际应用及实验发现，极限学习机隐含层节点的数目对神经网络的辨识精度有较大影响，通常为了达到一定精度要求，采用的办法是增加隐含层节点数目，这不仅增大了网络的复杂度，还往往出现过拟合问题，即训练精度增大时，测试精度却在下降。同时，在文献[6]中已经证明，极限学习机输入权值的选择对网络结果也有很大的影响，随机选择的权值容易产生作用很小，甚至无用的节点。本文提出一种思维进化极限学习机算法（MEAELM）。该算法主要利用思维进化算法优化极限学习机的输入权值和阈值，从而得到隐含层节点数更少、精度更高的网络。

该算法的主要实现过程为：

1）参数初始化。设定种群的大小popsize，一般取100-400个；优胜子群体个数bestpopsize，临时子群体个数temppopsize，一般取5-10个；每个优胜子群体和临时子群体中个体的数目通常保持一致，且使两种子群体的所有个体的数量和为popsize。个体由输入权值矩阵和阈值向量构成，个体长度L=m·l+l，其中m为输入层神经元数目，l为隐含层神经元数目。根据测试精度要求设定迭代次数iterate，可取5-50。

2）参数优化。各子群体执行趋同和异化操作，趋同和异化过程中利用训练样本，根据ELM算法中公式计算输出矩阵β，再利用测试样本一计算出每个个体的均方根误差（RMSE），将RMSE作为进化得分，得分函数也可以是别的参数表示。经过不断趋同、异化、迭代，输出最优个体。解码最优个体，得到最优的输入权值矩阵和阈值向量。

3）结果输出。根据最优解码个体，按照ELM算法公式，并利用测试样本二的数据得到输出权值矩阵β。

4 仿真实验

为了验证MEAELM实际效果，本文利用回归拟合实验进行测试，拟合函数如式(1)，并与ELM和BP神经网络拟合效果进行比较。

评价网络性能主要考虑两个参数——时间和误差。本文采用训练时间来衡量网络计算速度，采用预测值的均方根误差（Root Mean Square Error,，ti为预测输出值，yi为实际输出值，k为预测样本总数）和预测值的平均绝对相对误差（Average Absolute Relative Error,来定量描述网络预测精度。

4.1 迭代次数对MEAELM的影响

根据式(1)选取2 000组数据，x1和x2在[-5,5]范围内均匀产生，再随机选择1 800组训练数据、剩余200组中的随机选取100组作为测试数据一，剩下100组为测试数据二。测试数据一的预测输出均方误差的倒数作为MEAELM的得分函数使用。测试数据二是为了验证网络性能。

设置MEAELM的隐含层节点数为10，迭代次数从1增大到9，测试网络性能。因随机值的选取容易使结果产生波动，所以为了减小测试误差，最终测试结果为连续15次操作的平均值（下同），测试结果如表1所示。

表1 迭代次数对MEAELM的性能影响

从表1可以看到，训练时间较长，且随着迭代次数增大不断增加。RMSE和AARE较小，也随着迭代次数增大不断减小，但误差减小幅度逐渐变慢。

4.2 隐含层节点数对MEAELM、ELM和BP神经网络的影响

不断增加隐含层节点数目，比较MEAELM、ELM和BP神经网络拟合非线性函数(1)的能力。

选取式（1）所采集的数据，随机选择1 800组数据作为MEAELM、ELM和BP神经网络的训练数据，剩余200组中的随机选取100组作为测试数据一，剩下100组测试数据二，测试数据一的预测输出误差的倒数作为MEAELM的得分函数使用，测试数据二用来验证MEAELM、ELM和BP神经网络的网络性能。固定MEAELM的迭代次数为5。BP神经网络采用MATLAB自带工具箱函数构建、训练和测试网络，节点传递函数为tansig。测试结果如表2所示。

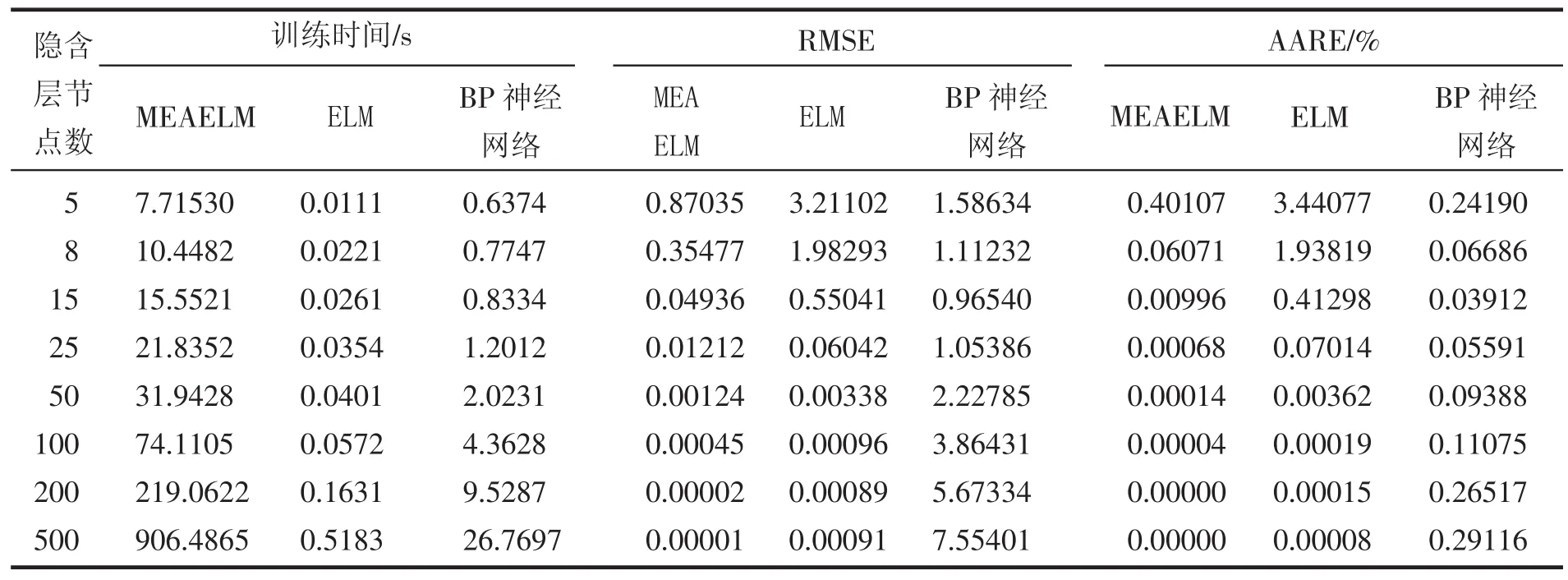
表2 隐含层节点数对MEAELM、ELM和BP神经网络的影响

从表2可以看到，MEAELM与ELM的RMSE和AARE随着隐含层节点数的增加而不断减小，BP神经网络的RMSE和AARE却呈现先减小后增大的结果。当隐含层节点数大于200时，MEAELM的AARE几乎为零。MEAELM的RMSE和AARE远远小于其他两种算法。同时也可以看到，MEAELM的训练时间较长，这主要由于输入权值和隐含层阈值参数的优化时间较长造成的。

4.3 其他函数拟合能力比较

为了进一步比较MEAELM在拟合方面的应用优势，利用其他函数比较MEAELM、ELM和BP神经网络的性能。函数如下：

对式(2)(3)(4)分别采集2000组数据，随机选取1800组作为训练数据，剩余200组中选取100组作为测试数据，对剩余100组数据进行预测，取所得预测结果的均方误差的倒数作为MEAELM的得分函数。设定目标预测AARE= 0.01%，测试三种算法所需隐含层节点数及训练时间。隐含层节点数从2开始增大，上限为300个。测试结果如表3所示。

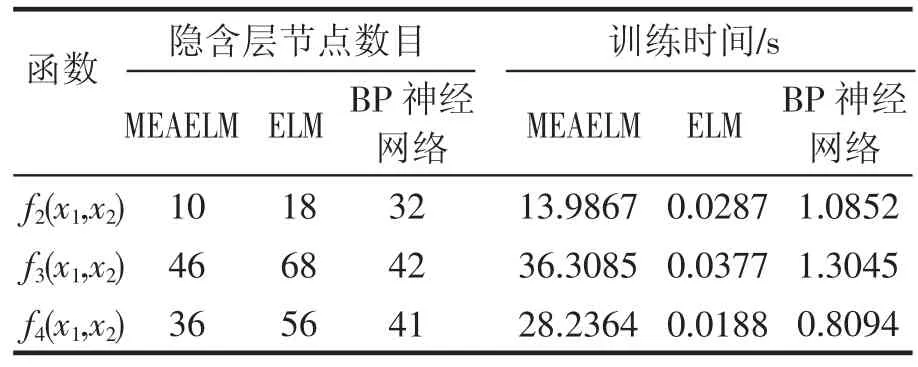
表3 三种算法对不同函数目标预测AARE=0.01%的性能比较

从表3可以看到，同一算法对不同函数拟合效果不同，但在同一AARE为0.01%下，MEAELM相对与ELM和BP神经网络所需隐含层节点数更少，网络更简单。仿真实验发现，对每个函数重复15次操作中，MEAELM和ELM所需隐含层节点数比较稳定，而BP神经网络所需隐含层节点数变化较大，甚至对式(3)仿真时出现隐含层节点数最多和最少相差211个的情况，非常不利于网络的合理建立。

5 结论

本文提出了一种思维进化极限学习机算法，该算法的基本思想是利用全局搜索能力极强的思维进化算法来优化极限学习机的输入层权值和隐含层阈值；最终目的是为了减少隐含层节点数，降低网络复杂度，提高网络预测精度。该算法结合了MEA和ELM的优点，具有参数调整简单、泛化能力强、全局优化能力强等特点。通过函数拟合仿真实验，并与ELM和BP神经网络算法比较，结果表明，该算法可以用较少的隐含层节点数取得更高的预测精度，达到了预期效果。

[1]Huang G B,Zhu Q Y,Siew.Extreme learning machine：a new learning scheme of feedforward neural networks[J].Neurocomputing,2004,2(2)：985-990.

[2]Deng W,Chen L.Color imagewatermarking using regularized extreme learning machine[J].Neural Network World,2010,20(3)：317-330.

[3]Zong W W,Huang G B.Face recognition based on extreme learning machine[J].Neurocomputing,2011,74 (16)：2541-2551.

[4]Huang G B,Zhu Q Y,Siew C K.Extreme learning machine Theory and applications[J].Neurocomputing, 2006,70：489-501.

[5]Huang G B,Wang D H,Lan Y.Extreme learning machines：a survey[J].International Journal of Machine Learning and Cybernetics,2011,2：107-122.

[6]杨易旻.基于极限学习的系统辨识方法及应用研究[D].长沙：湖南大学,2013：29-30.

[7]Sun C Y.Mind-Evolution-Based Machine Learning：Framework and the Implementation of Optimization[M]// Proceedings of IEEE International Conference on Intelligent Engineering Systems.Vienna,Austria, 1998,355-359.

[8]Sun Y,Sun C Y.Clustering and Reconstruction of Color images Using MEBML[M]//Proceedings of International Conference on Neural Networks&Brain.Beijing, China,1998,361-365.

[9]Cheng M Q.Gray image segmentation on MEBML frame[J].Intelligent Control and Automation,2000(1)：135-137.

[10]韩晓霞,谢克明.基于思维进化算法的模糊自寻优控制[J].太原理工大学学报,2004,35(5)：523-525.

[11]Huang G B.Learning capability and storage capacity of two-hidden-layer feedforward networks[J].IEEE Transactions on Neural Networks,2003,14(2)：274-281.

（责任编辑：李堆淑）

An Extreme Learning Machine Optimized by MEA and Its Applications

LIU Jun
(Cellege of Electronic Information and Electrical Engineering,Shangluo University,Shangluo726000, Shaanxi)

Extreme Learning Machine（ELM）is a new type of neural network with hidden layer feedforward.Compared with traditional neural network training method,ELM is endowed with good generalization ability,fast learning rate,etc.Input weights and thresholds randomly produced lead to useless number or number of little value.More often than not,hidden layer nodes are added to achieve the ideal accuracy.A new ELM learning algorithm,which was optimized by mind evolutionary algorithm(MEA),was proposed.In order to reduce the hidden layer nodes and increase network prediction accuracy,MEA was used to optimize input weight matrix and threshold vector,then the output weights could be calculated by Moore-Penrose generalized inverse.To test the validity of proposed method,the function fitting simulation experiments were drawn.Compared to ELM algorithm and BP neural network algorithm,experimental results showed that the proposed algorithm achieved better performance with less hidden layer nodes.

mind evolution;Extreme Learning Machine;weight;threshold

TP181

A

1674-0033（2015）02-0012-04

10.13440/j.slxy.1674-0033.2015.02.004

2014-12-27

刘俊，男，山西大同人，硕士，助教