基于椭球变换的高原矿区GPS控制网的建立方法*

王瑞祥，徐晓艳，王 坤，杨 亮

(1.云南能源职业技术学院 资源与环境工程学院，云南 曲靖 655000； 2.云南省地矿测绘院，云南 昆明 650218)

基于椭球变换的高原矿区GPS控制网的建立方法*

王瑞祥1，徐晓艳1，王 坤2，杨 亮2

(1.云南能源职业技术学院 资源与环境工程学院，云南 曲靖 655000； 2.云南省地矿测绘院，云南 昆明 650218)

阐述了在高原矿区建立独立GPS控制网时如何通过几种椭球变换的方法获得GPS控制网起算点坐标的方法，并通过某矿区D级GPS控制网的建立，比较几种椭球转换方法的特点及其对GPS网二维约束平差精度的影响。

GPS控制网；独立坐标系；椭球变换；起算点

0 引言

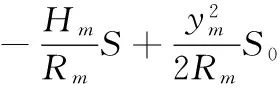
1 国家坐标系控制点转换为独立坐标系起算点的实现

1.1 椭球膨胀法

1.1.1 椭球膨胀法的基本思想

椭球膨胀的基本思想是保持椭球中心及椭球扁率不变，仅改变椭球的长半轴a，对椭球进行缩放，使缩放后的椭球面与独立坐标系的投影面相切。根据椭球大地测量学广义大地测量学微分公式可知[3]，变形前后的大地坐标和da的关系如下：

(1)

式中：da为椭球长半轴的变化量；M为子午圈曲率半径；N为卯酉圈曲率半径；H为大地高。

而椭球的长半轴da的缩放量可以通过以下常用的3种方法实现[4]：

1)将投影面的平均大地高直接加到国家椭球长半轴上，即da=Hm；

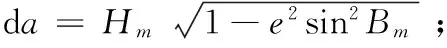
1.1.2 椭球膨胀法坐标转换的实现

在确定了大地坐标和椭球长半轴增量的关系后，可将原椭球下的大地坐标转换为新椭球下的大地坐标，然后以新椭球为基准利用高斯投影正算公式，求出独立坐标系坐标，作为独立坐标系的起算点，以1980西安坐标(简称西安80坐标)转换到独立坐标为例，转换过程如下：

1)确定测区中心基点在西安80坐标系下的大地坐标(B L H)西安80；

2)通过长半轴的增量计算独立坐标系的大地坐标增量(dB dL dH)得到独立坐标系下的大地坐标(B L H)独立；

3)仅改变原椭球的长半轴，得到新的椭球参数，在新椭球参数下利用高斯投影正算公式计算独立坐标系下的高斯平面直角坐标。

1.2 椭球平移法

1.2.1 椭球平移法的基本思想

如果不改变椭球形状和大小，即不改变椭球参数，而是将椭球沿测区中心所在的基点的法线方向平移，使参考椭球面与独立坐标系的投影面相重合，也可将国家坐标系的控制点成果换算到独立坐标系下。此时，测区中心的纬度B和经度L不变，大地高减小ΔH；由空间直角坐标同大地坐标的转换关系[5]：

(2)

得独立坐标系椭球中心在原国家坐标系椭球下的坐标为[6]：

(3)

式中：ΔH为平移后基准点的大地高变化量，取值为负；B0、L0为基准点的纬度和经度。根据椭球大地测量学广义大地测量学微分公式可知[7]，其数据特征如下：

(4)

1.2.2 椭球平移法坐标转换的实现

以1980西安坐标为例，将国家坐标转换为独立坐标的过程如下：

1)确定测区中心基准点在西安80坐标系下的大地坐标(B L H)西安80；

2)将西安80的大地坐标转换为地心坐标(X Y Z)西安80；

3)计算将椭球中心平移后的地心平移量(dX dY dZ)；

4)根据直角坐标增量与大地坐标的关系确定独立坐标下基准点的大地坐标增量(dB dL dH)得到独立坐标系下的大地坐标(B L H)独立；

5)利用高斯投影正算高斯，计算独立坐标系下的高斯平面直角坐标。

1.3 椭球变形法

1.3.1 椭球变形法的基本思想

对于椭球变形法，保持变形前后椭球中心、坐标指向、尺度参数不变，先将椭球面沿测区中心基准点法线方向膨胀到独立坐标系的投影面，然后改变椭球扁率f，使得基准点在法线处重合，基准点处的经纬度不发生改变[8]。计算公式为：

(5)

其大地坐标变化量为：

(6)

1.3.2 椭球变形法坐标转换的实现

椭球变形法坐标转换过程与椭球膨胀法类似，在此不再赘述。

2 椭球变换的几种方法在矿区GPS首级控制网中的应用

以云南某矿区为例，该矿区地处东经103° 58′～ 104°49′、北纬25°02′～ 25°58′之间，东西宽约4 km，南北长约7 km。地貌以滇东高山河谷地形为主，矿区平均海拔1 860 m，最大高差约200 m，位于河谷平缓区，东部及南部山势较高，西部稍显平缓。测区内有3个西安80国家二等点，测区大地水准面与参考椭球面的差距为29 m。为了限制长度综合变形，取标准中央子午线105°和1 430 m的抵偿高程面进行投影，建立矿区独立坐标系。矿区共布设了20个D级GPS控制点，并得到了合格的三维平差成果，现通过上述几种椭球转换的方法，分别对3个国家二等控制点坐标进行转换，并利用转换结果进行二维约束平差[9-10]，对椭球转换结果及二维平差结果进行对比分析，结果见表1、表2、表3。

从表1-3可知：虽然椭球长半轴的变化da选取的方法不同，但利用椭球膨胀的方法得到的椭球变换3组成果较为接近；对于不同的转换模型，得到的坐标成果有所差别，其中椭球膨胀法和椭球变形法得到的高斯平面坐标较为接近，椭球平移法与其他方法相比较其坐标在数值上差别较大，但3种方法投影后的距离及投影面坐标方位角及GPS二维约束平差结果基本一致。

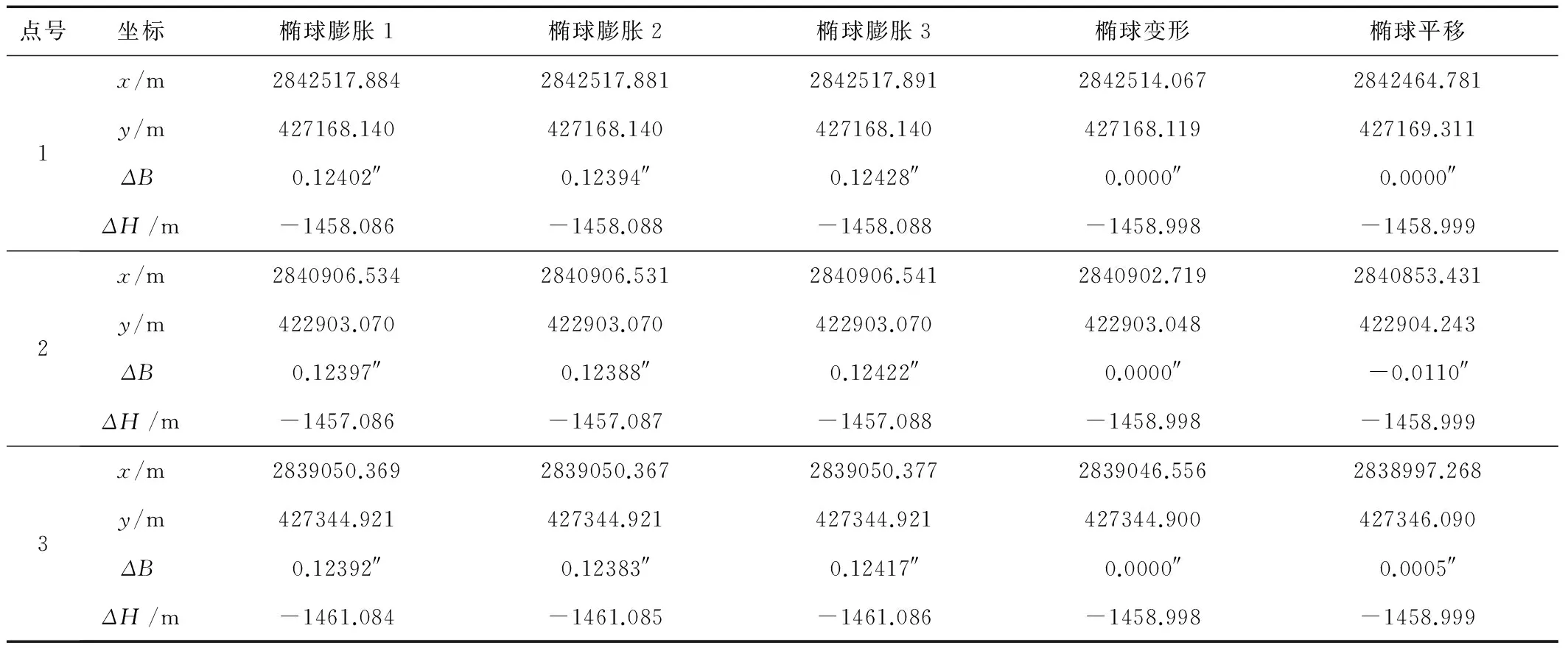
表1 几种椭球变换结果比较Tab.1 Comparison among several ellipsoid transformation results

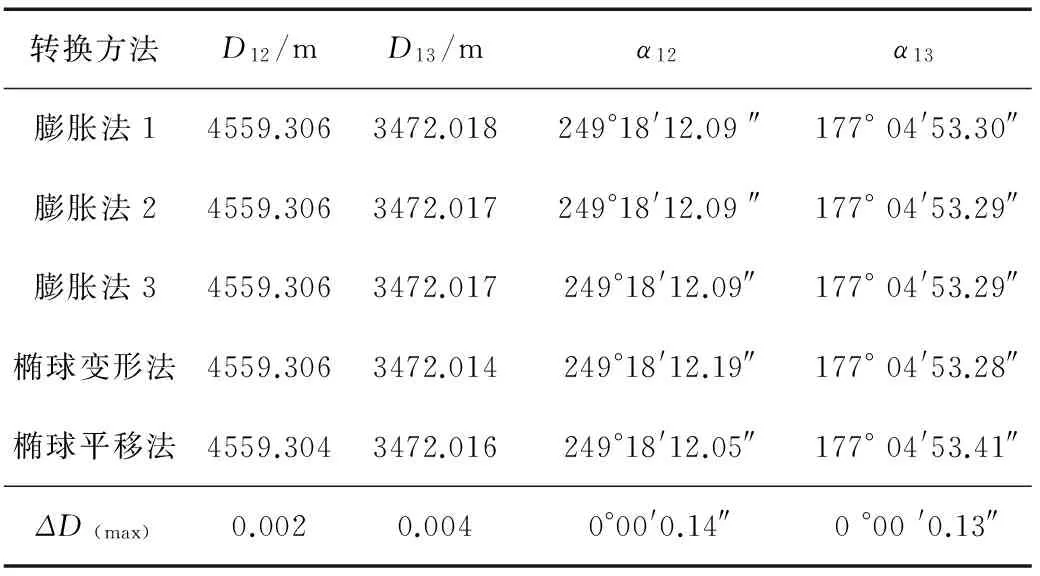
表2 几种椭球变换投影面边长及方位角比较Tab.2 Comparison of azimuth and projection plane side length among several ellipsoid transformations

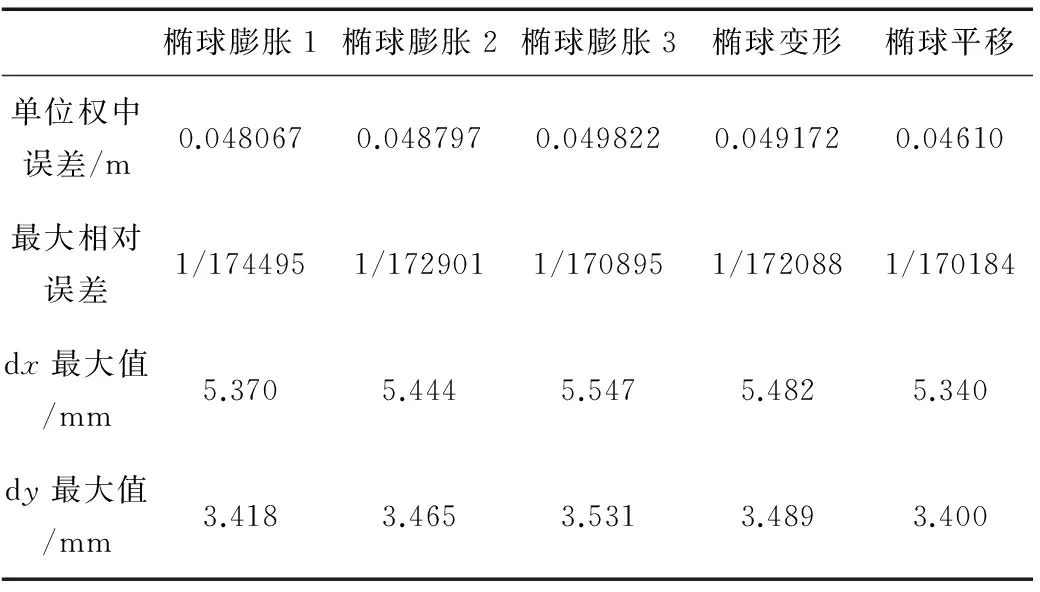
表3 几种椭球变换GPS二维平差结果比较Tab.3 Comparison of GPS two-dimensional adjustment results among several ellipsoid trasformations

3 结论

通过分析，笔者得出如下结论：

1)对于中小区域的矿区控制测量而言，如果利用椭球膨胀求起算点坐标，长半轴的变化直接取投影面大地高Hm最为方便。同时，由于在几种椭球变换方法中，椭球膨胀方法最为简单，所以可作为中小矿区工程应用的首选方法。

2)椭球变形法投影后的经纬度不发生改变，这对于独立坐标系与国家坐标系的衔接具有重要意义。虽然不改变参考椭球面原有的大地经纬度，从理论上来讲是不严密的，但对于中小矿区而言，其影响较小。所以，为了和国家坐标成果相联系，也可采用椭球变形法建立独立坐标系。

3)上述几种方法，均是基于单点进行转换，事实上，两个投影面之间尚存偏离，且离转换基点越远，其误差越大。所以对于转换基点应尽可能选择在测区中央，且高程和抵偿面高程接近。

[1] 孔祥元.控制测量学[M].武汉：武汉大学出版社，2009.

[2] 煤炭工业部生产司.煤矿测量手册[M].北京：煤炭工业出版社，1979：77-78.

[3] 熊介.椭球大地测量学[M].北京：解放军出版社，1988.

[4] 丁士俊，畅开蛳，高琐义.独立网椭球变换与坐标转换的研究[J].测绘通报，2008(2)：4-6.

[5] 张凤举.控制测量学[M].北京：煤炭工业出版社，1999.

[6] 李世安，刘经南，施闯.应用GPS建立区域独立坐标系中椭球变换的研究[J].武汉大学学报：信息科学版，2005(10)：888-891.

[7] 海清.通过椭球变换建立区域独立坐标系的方法[J].测绘与空间地理信息，2008，31(1)：168-169.

[8] 王国祥.基于工程椭球的地方坐标系坐标换算模型比较分析[J].铁道勘察，2014(3)：1-4.

[9] 刘大杰.全球定位系统(GPS)定位原理与数据处理[M].上海：同济大学出版社，1996.

[10] 马少君.GPS控制网数据处理方法[D].上海：同济大学，2008.

Methods of Establishing GPS Control Network in Plateau Mining Area Based on Ellipsoid Transformation

WANG Rui-xiang1，XU Xiao-yan1，WANG Kun2，YANG Liang2

(1.FacultyofResourcesandEnviromentEngineering，YunnanVocationalInstituteofEnergyTechnology，QujingYunnan655000； 2.YunnanInstituteofSurveyingandMappingofGeologyandMineralResources，KunmingYunnan650218，China)

This paper expounds how to obtain starting points’ coordinates of GPS control network by means of several ellipsoid transformation methods when setting up independent GPS control network in plateau mine area.By the estiblishment of a GPSD-level contral network，the characteristics of several ellipsoid transformation methods and their imfluence on the accuracy of two-dimensional constrained adjustment of GPS network are compared.

GPS control network；independent coordinate system；ellipsoid transformation；starting points

2015-06-17

P 226+.3； P 282.2

B

1007-9394(2015)04-0033-03

王瑞祥(1985～)，男，云南普洱人，助教，现主要从事控制测量、工程测量等方面的教学研究工作。