倾斜山坡地块面积的精确量算与精度分析*

程效军，程帆瑾

(1.同济大学 测绘与地理信息学院，上海 200092； 2.湖南大学 信息科学与工程学院，湖南 长沙 410082)

倾斜山坡地块面积的精确量算与精度分析*

程效军1，程帆瑾2

(1.同济大学 测绘与地理信息学院，上海 200092； 2.湖南大学 信息科学与工程学院，湖南 长沙 410082)

对于倾斜山坡上多边形地块，利用电子全站仪测定该地块中的转折点的三维坐标，先按其中3点求出初始平面方程；然后以此为基础，按最小二乘法的间接平差原理，解算出初始平面方程式系数的改正值，得到拟合的倾斜平面方程式；计算该平面与水平面的夹角，然后求出该地块投影到水平面上的面积，由该面积和夹角即可精确计算出地块的倾斜面积；最后对该地块的面积精度进行评定。

倾斜山坡；地块面积；精确量算；精度分析

0 引言

在实际工作中，往往会遇到如何精确量算倾斜山坡地块面积的问题。如对于山地中的绿化面积进行计量等。如图1所示，倾斜面上的地块为n边形(n>3)，利用电子全站仪测定该地块的转折点P1、P2、P3，…，Pn的三维坐标，先按P1、P2、P3三点求出其初始平面。然后以此为基础，按最小二乘法的间接平差原理，列出各点观测值的误差方程式，组成法方程式，解算出初始平面方程式系数的改正值，得到拟合的平面方程式[1]。计算该平面与水平面的夹角，然后求出该地块投影到水平面上的面积，由该面积和夹角即可精确计算出地块的倾斜面积。另外根据误差传播定律，可推出该地块在斜面上的面积中误差公式[2]。

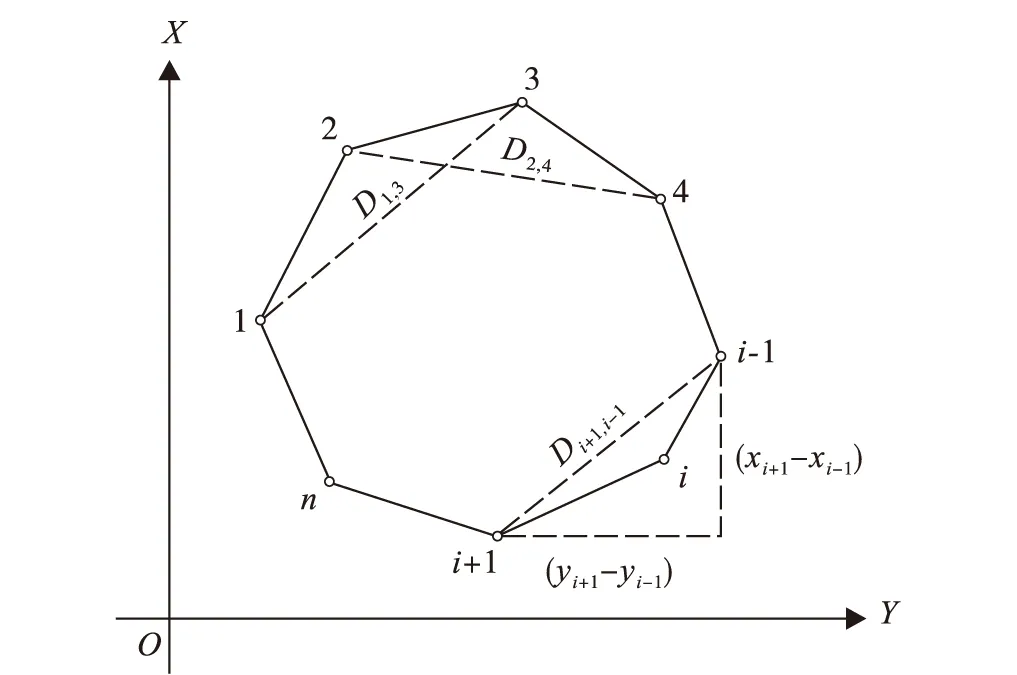
图1 n边形的倾斜地块Fig.1 N-gon’s tilt block

1 计算公式

如图1所示，设P1、P2、P3三点的坐标为(x1，y1，z1)，(x2，y2，z2)，(x3，y3，z3)，由这3点构成的平面，可用下式表示：

(1)

将式(1)展开，可得到包括P1、P2、P3三点的平面方程式：

A0x+B0y+C0z+D0=0

(2)

式(2)中：

(3)

设按测定的n点拟合出的平面方程式应为：

Ax+By+Cz+D=0

(4)

将式(4)同除以D可得：

(5)

令

(6)

则式(4)可改写为：

A′x+B′y+C′z+1=0

(7)

对于每个测定点的观测值可列出其误差方程式：

vi=A′xi+B′yi+C′zi+1 (i=1，2，…，m)

(8)

(9)

(10)

式(10)中，δA′，δB′，δC′为未知参数，右端括号内数值为常数项li。根据n个地面观测点的误差方程式组成法方程式，再按照平方根法对法方程式求逆，可解得未知数δA′，δB′，δC′，由此求得平面方程的系数：

(11)

根据倾斜平面方程与水平面方程，可计算出斜面的夹角，公式为：

(12)

将P1、P2、P3，…，Pn投影到水平面上，计算该地块在水平面上的面积，公式为：

(13)

最后按计算该地块在倾斜面上的面积，公式为：

(14)

根据误差传播定律，可推出该地块在倾斜面上的面积中误差公式：

(15)

式中：mc=mx=my；Di+1，i-1为图1中第i点的左、右相邻点的连线的长度。

2 应用实例

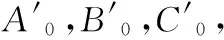
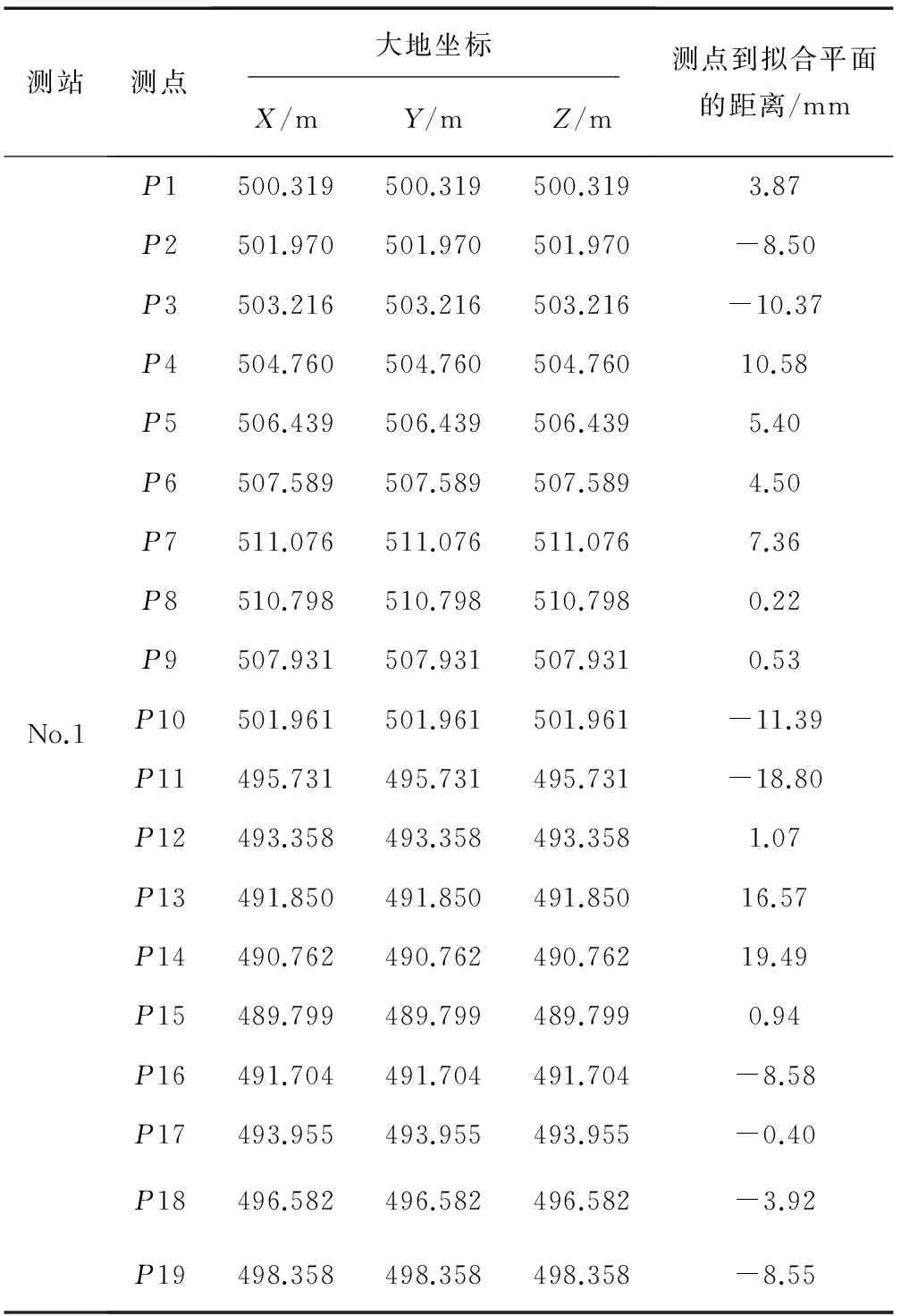
表1 倾斜地块各顶点坐标Tab.1 Coordinates of certain tilt block

表2 倾斜地块拟合平面计算结果Tab.2 Fitting plannar calculation results of certain tilt block

由表2可知该地块拟合出的平面方程为：

0.00016205X-0.00202449Y-0.01642770Z+1=0

按式(12)可计算出该倾斜平面的倾角为：

α=8°57′08″

按式(13)计算该地块投影在水平面上的面积为：

P=165.260 2 m2

按式(14)计算该地块在倾斜面上的面积：

P′ = 166.518 4 m2

可见，该地块在倾斜面上的面积与投影在水平面上的面积相差1.258 2 m2，相对精度达1/130。

用2秒级的电子全站仪在200 m范围内点位精度可达mc=mx=my=±0.010 m，按式(15)计算该地块在倾斜面上的面积中误差：

mP=±0.129 7 m2

则该地块的面积相对中误差为：

从表1可知，由于倾斜地块为草地，点位测定存在一定的误差，该地块的平面拟合精度为±10.35 mm，与实际情况相符。

3 结论

对于倾斜山坡上地块，可以利用电子全站仪测定该地块的各个转折点的三维坐标，拟合出该地块的平面方程式，求出该地块投影到水平面上的面积，由该面积和夹角即可精确计算出地块的倾斜面积及其中误差，从而使计算出面积更加符合实际情况。

[1] 潘正风，程效军，成枢，等.数字地形测量学[M].武汉：武汉大学出版社，2015.

[2] 顾孝烈，鲍峰，程效军.测量学 [M].第4版.上海：同济大学出版社，2011.

[3] 李杰，程效军.三维激光扫描仪在墙面平整度检测中的应用[J].井冈山大学学报：自然科学版，2014(4)：13-17.

Accurate Measurement and Calculation with Accuracy Analysis of Block Area on Tilt Hillside

CHENG Xiao-jun1，CHENG Fan-jin2

(1.CollegeofSurveyingandGeo-informations，TongjiUniversity，Shangshai200092，China； 2.CollegeofComputerScienceandElectronicEngineering，HunanUniversity，ChangshaHunan410082，China)

To the polygonal block on tilt hillside，we use electronic total station to determine the 3D coordinates of the block’s turning points.First，we use the three points of coordinates to obtain the initial plane equation.Second，according to the adjustment of observation equations of the least square method，the correcting value of initial plane equation’s coefficients is calculated，and the fitting tilt plane equation is obtained.Third，we calculate the angle between the plane and horizontal plane，and the projected area of the block to the horizontal plane is obtained.Then the tilt area of the block can be calculated out accurately by using the area and the angle.At last，the accuracy of the land area will be evaluated.

tilt hillside；land area；accurate measurement and calculation；accuracy analysis

2015-09-11

P 218

A

1007-9394(2015)04-0001-02

程效军(1964～)，男，江西乐平人，教授，博士生导师，工学博士，主要研究方向为三维数字仿真与精密工程测量。