基于改进支持向量机的深基坑变形预测*

吴 欢，周春波，秦 昆

(1.江西环境工程职业学院，江西 赣州 341000； 2.江西省水土保持科学研究院，江西 南昌 330029； 3.江西省煤田地质局测绘大队，江西 南昌 330029)

基于改进支持向量机的深基坑变形预测*

吴 欢1，周春波2，秦 昆3

(1.江西环境工程职业学院，江西 赣州 341000； 2.江西省水土保持科学研究院，江西 南昌 330029； 3.江西省煤田地质局测绘大队，江西 南昌 330029)

深基坑变形监测与预测是深基坑设计施工中的一个重要的环节，准确地预测深基坑未来的变形，是深基坑变形监测的最终目的。针对传统常用预测方法存在一定的局限性这个问题，结合支持向量机的研究现状，提出将能够有效地解决小样本、非线性、高维数、局部极小等问题的支持向量机模型应用于深基坑变形预测的方法。具体方法是：采用粒子群算法对支持向量机的相关参数进行寻优，得到改进支持向量机预测模型，然后将其预测结果与传统的支持向量机模型、Elman动态神经网络模型预测结果进行比较，最后采用均方误差、平方和误差、平均相对误差对预测效果进行评价。实验结果表明，基于改进支持向量机预测模型用于变形预测是可行的，且能更好地反映深基坑系统的动态非线性特点，具有一定的优越性与工程应用推广价值。

深基坑；变型预测；改进的支持向量机

0 引言

变形(Deformation)是指在各种影响因素的作用下，变形体的大小、形状、位置在时空域中的变化，是自然界普遍存在的现象[1]。当变形体的变形不超过一定允许的范围内，是不会造成危害的，但若超过这个允许值，则可能引发灾害，如地震、采矿塌陷、坝内蜂窝、火山爆发、滑坡、桥梁的垮塌等灾害。上述这些灾害的发生与变形息息相关，因此在变形监测这个领域，国内外学者已对其进行了广泛的关注与研究。

近年来，深基坑在数量以及难度上都有了大幅度的提升，由此带来的环境公害问题也十分突出，基坑事故时有发生，给社会造成了严重的影响。例如：1998年，广东省珠海市发生了一起深基坑坍塌特大事故；2005年，广州市海珠区发生了深基坑坍塌的重大生产安全事故；2008年，杭州地铁某站发生深基坑坍塌事故等。

为了避免工程事故的发生，人们已经认识到现场监测是十分重要的。因此，开展深基坑工程的监测分析，探讨深基坑开挖引起的变形特性，对进一步完善深基坑支护工程设计，减少事故发生频率具有十分重要的理论和现实意义[2-3]。由于深基坑工程现场监测数据序列中包含着系统信息的演化，所以设计施工人员希望能从这些数据中找出其蕴含的规律，并用这些观测数据来预测系统未来的发展动态，反馈于原设计，以便及时调整施工方案，或采取应急对策[4]。目前，基坑工程所采用的预测方法多种多样，如灰色预测、时间序列分析、BP神经网络等方法[4-7]。

关于以上这些预测模型，均有一定的局限性，由于深基坑受到外力作用，并且外力作用具有复杂性与不确定性，除此之外，还包括一些其它的不确定性因素，在这种情况下，想要建立适合的确定性模型来对深基坑变形进行预测变得十分困难，这个问题一直没有得到较好的解决。为此，通过揭示变形监测数据序列的结构与规律，建立动态预测模型，推断变化趋势，反映变形特性，是一种有效的方法[8]。而作为最近才发展起来的新型机器学习算法——支持向量机给建立深基坑变形预测模型提供了机会，为深基坑变形预测提供了一种新方法。

支持向量机进行建模预测过程中，如何选择合适的支持向量机核函数以及相关参数，是一个必须面临的重大问题。换句话说，上述参数的选取将直接影响利用支持向量机进行预测的结果，但到目前为止没有一种较为成熟的方法。针对此情况，本文结合优化算法来优选支持向量机的参数，并应用改进后的支持向量机模型对深基坑的变形进行预测。

1 SVM原理

支持向量机是一种基于结构风险最小化(SRM)准则的机器学习算法，具有很好的泛化能力，能够有效地解决小样本、非线性、高维数、局部极小等问题[9]。支持向量机也可以称为支持向量网络，且具有其他传统预测方法所没有的优越性。一些学者认为，统计学习理论(Statistical Learning Theory，简称SLT)和支持向量机(Support Vector Machine，简称SVM)正在成为继神经网络研究之后新的研究热点，并将有力地推动机器学习理论和技术的发展[10]。目前，SVM已成为国内外研究的热点。

支持向量机最开始是为了解决分类问题而提出的，支持向量机主要包括非线性回归和模式识别，两者之间有很多的相似性，但还是有细小的区别。模式识别主要用于分类和特征点的提取，它们的应用非常广泛。后来通过Vapnik引入ε不敏感损失函数，提出将SVM的分类推广至回归，其可应用于预测方面。

在支持向量机回归(Support Vector Machine for Regression，简称SVR)中，它的数学提法与分类问题相近，变量y(期望输出)的取值如下：

1)在分类问题中，变量y只是由两个数值所代表。

2)在回归问题中，变量y可以取任意数值。支持向量回归具有坚实的理论基础，是建立在SVM思想上的回归算法，分为线性回归和非线性回归[9]。

支持向量机回归模型能够很好地解决非线性回归问题。该方法具有学习速度快，全局最优和泛化能力强等优点，其学习结果明显好于其它传统的回归预测方法[11]。目前主要有ε-SVR和v-SVR两种方式，本文采用ε-SVR对深基坑变形预测问题进行研究。

2 深基坑变形分析

深基坑变形的影响因素有确定性因素和不确定性因素，而且每种影响因素对其作用情况是不相同的。其影响因素，如表1所示。

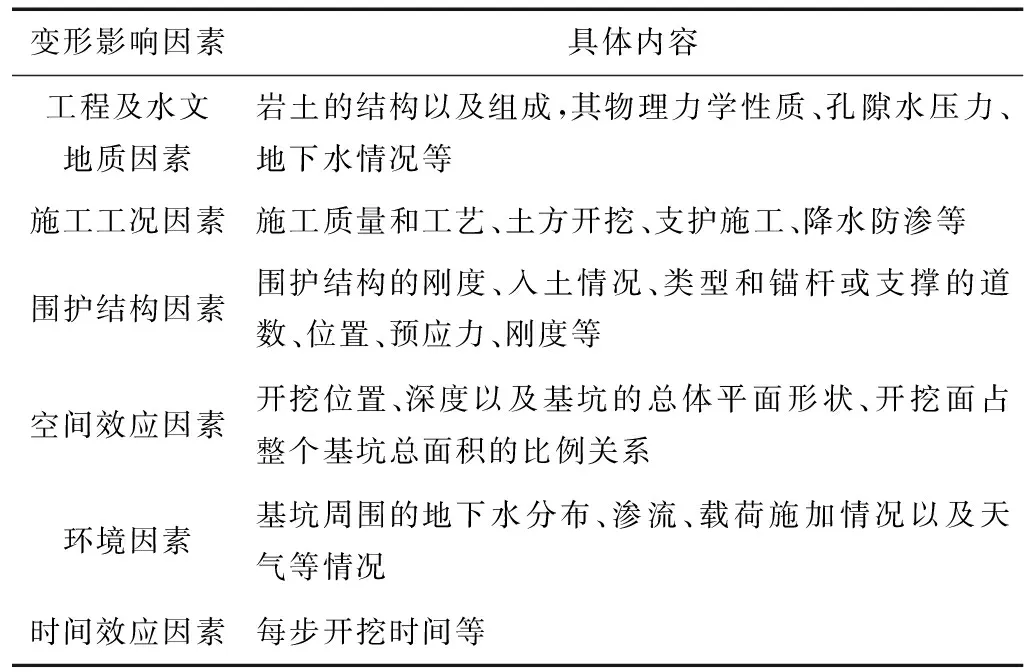
表1 基坑变形影响因素Tab.1 Influencing factors of deformation for deep foundation pit

3 深基坑变形预测对象

根据国家标准规范规定，深基坑变形监测项目主要为：桩顶水平位移及沉降、周边建筑物沉降及倾斜、立柱沉降、桩体测斜、支撑内力、周边地下水位和周边土体测斜等。

深基坑开挖变形主要有深基坑底部的隆起、围护结构的变形、周围地层的移动这3种变形，如果某种变形发生明显变化，则其它两种变形的变形量必然会变大。在整个基坑的施工过程中，根据相关研究发现，围护墙体水平位移和地表沉降会引起很大的危害，因此在施工中，它们是重点监测的对象。

本文根据以上情况，选取深基坑围护桩桩体测斜(深层水平位移)进行预测。在支护方案确定时，对于同一时间层面来说，桩体变形的影响因素可以总结如下：无支撑暴露时间、施工参数及开挖深度等。由于整个深基坑施工过程是处于一个不断变化的动态过程的状态，所以这些因素为串行变量，预测的结果决定了这些因素。对于本文中预测的深基坑围护桩桩体变形，采用的是与桩体变形有关的各类影响因素综合反映的前一段时间的位移观测数据，这里的位移观测数据就是串行变量。

所以，根据上面的分析，采用同一位置的前一段时间的位移观测值去预测后续的位移值，这符合预测的数学含义，又能使数据采集变得更容易，还可以提高预测的可信度、可操作性以及预测精度。

4 PSO 原理

Kennedy和Elberhart根据对鸟群觅食行为的研究，在1995年提出了粒子群算法(Particle Swarm Optimization，简称PSO)[14-15]，其思想来源于人工生命和演化计算理论。PSO采用简单的速度—位置搜索模型，用粒子的位置表示待优化问题的解，每个粒子性能的优劣程度由待优化问题的适应度函数值决定，每个粒子由一个速度矢量决定其飞行方向和速率大小[16]。粒子飞行速度和位置按式(1)、式(2)进行更新，公式如下：

vid(t+1)=wvid+c1*r1*(pbid-xid(t))+c2*r2* (pgd-xid(t))

(1)

xid(t+1)=xid(t)+vid(t+1)

(2)

式中：w为惯性权重；xid为粒子的位置；vid为粒子速度；c1，c2为学习因子，取值范围一般在区间[0，2]之间；pbid为粒子的个体最优位置；pgd为全局最优解；r1，r2为分布在区间[0，1]内的两个随机独立数。粒子群算法执行流程示意图，如图1所示。

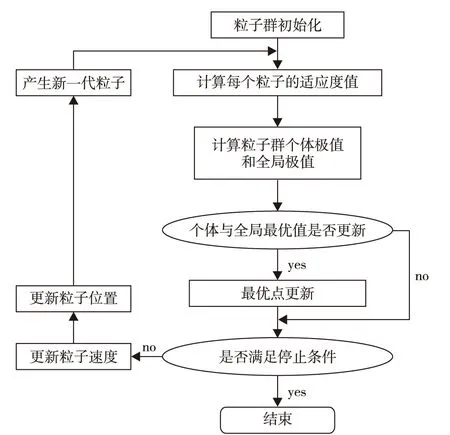
图1 粒子群算法流程示意图Fig.1 The flow of Particle Swarm Optimization

5 基于改进支持向量机的深基坑变形预测建模

基于改进的支持向量机的深基坑变形预测建模步骤如下：

第一步，建立训练学习样本集。选取嵌入维数为n，时间延迟为1，通过得到的嵌入维数以及时间延迟，建立输入相点Xi={xi，xi+1，…，xi+m-1}与输出相点Yi={xi+m}之间的映射关系，即相空间结构，进行单点单步预测。转换之后，变为学习样本。

第二步，根据交叉验证原理又将模型训练集分为训练集和验证集，采用PSO参数寻优算法对SVM模型的参数进行训练寻优。

第三步，设置PSO初始参数，包括种群大小、进化代数、学习因子c1和c2、粒子初始位置和速度、惯性权重因子、算法收敛精度等。

第四步，根据选取的RBF核函数，对待优化参数C、g、p，确定其约束范围，根据产生的实数编码初始化种群，这时每个粒子的维数为三维。

第五步，通过得到的训练样本集训练SVM模型，对训练集进行交叉验证，通过适应度函数即CV意义下的MSE来评价每一个粒子，计算它们的适应度值。比较每一个粒子当前适应度值，并与该粒子历经过的最优位置pbest进行比较，若优于pbest，则pbest被最好位置所代替。

第六步，对于种群中的每一个微粒子，将其适应度值与所有群体微粒子所经历过的最优位置的适应度值进行比较分析，如果小于所有种群微粒子经历过的最好位置的适应度值，则当前粒子的最优位置为全局最优位置gbest。

第七步，更新粒子的状态。利用式(1)、式(2)对每个粒子进行更新处理，以便产生下一代种群。

第八步，检查是否得到最优解，即判定终止条件。判断全局最优位置的适应度值是否能够满足设定的适应度值的最小目标精度值或者达到最大迭代次数与否，若满足的话，则寻优运算结束，便输出最优解C、g、p，然后对SVM模型进行重新训练学习，最后得到的模型为较好的改进SVM预测模型；否则返回到第二步。

第九步，利用预测集数据作为最优参数组合下的改进SVM模型的检验数据，计算出深基坑工程的变形预测值。

第十步，根据常用的预测精度评价指标对深基坑工程变形预测效果进行客观评价。

6 工程实例

本文选取广州某深基坑围护桩桩体作为研究对象，从布设的10个测斜孔中选取其测斜监测点CX6号孔6.5 m深度处的原始53期数据作为研究对象。利用本文提出的改进支持向量机预测模型与传统的支持向量机模型以及Elman动态神经网络模型的预测结果进行比较分析。实验中，选取前43期的深基坑围护结构桩体测斜数据用于建模，后面10期数据用于预测。

根据建立的SVM预测模型进行训练，对于嵌入维数n，由于不同的嵌入维数n对预测结果有一定的影响，分别取n为2，3，…，9，采用均方误差来评价预测的结果，根据建立的输入与输出之间的相空间结构映射关系，转换之后，成为学习样本。得出了当嵌入维数为3、时间延迟为1，核函数选用RBF函数时，预测精度最佳。

实验过程中，粒子群算法的相关参数设置，如表2 所示。利用MATLAB编写相关程序，实验程序在MATLAB7.14平台上编写，在台湾大学林智仁教授的libsvm工具箱函数基础上进行扩展编程计算，实验得到的最佳参数组合为：C=2.348 1，g=2.684 8，p=0.01。

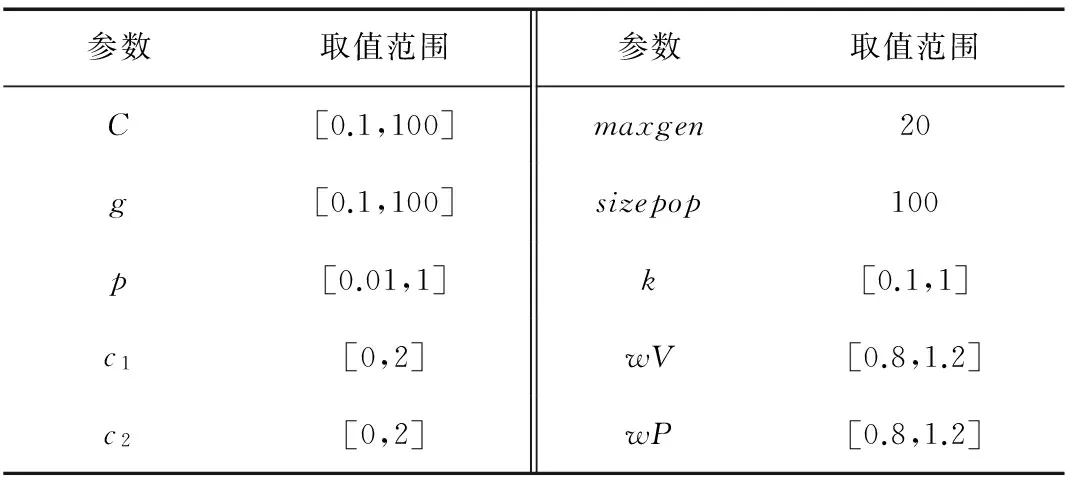
表2 PSO算法寻优实验条件Tab.2 The optimized experimental conditions of PSO algorithm

为了说明将粒子群优化算法和SVM理论相结合得到的改进支持向量机模型用于深基坑变形预测是完全可行的，利用本文提出的改进支持向量机预测模型与传统的支持向量机模型以及Elman动态神经网络模型的预测结果进行比较分析，结果见表3。

从表3可以看出，改进模型的预测精度要优于传统的支持向量机模型和Elman动态神经网络模型。其中，Elman动态神经网络的网络结构为 3 层，网络拓扑结构为3-9-1。L-M算法作为训练函数，采用tansig函数作为输入层至隐层的激励函数，采用纯线性函数Purelin作为隐层至输出层的激励函数。

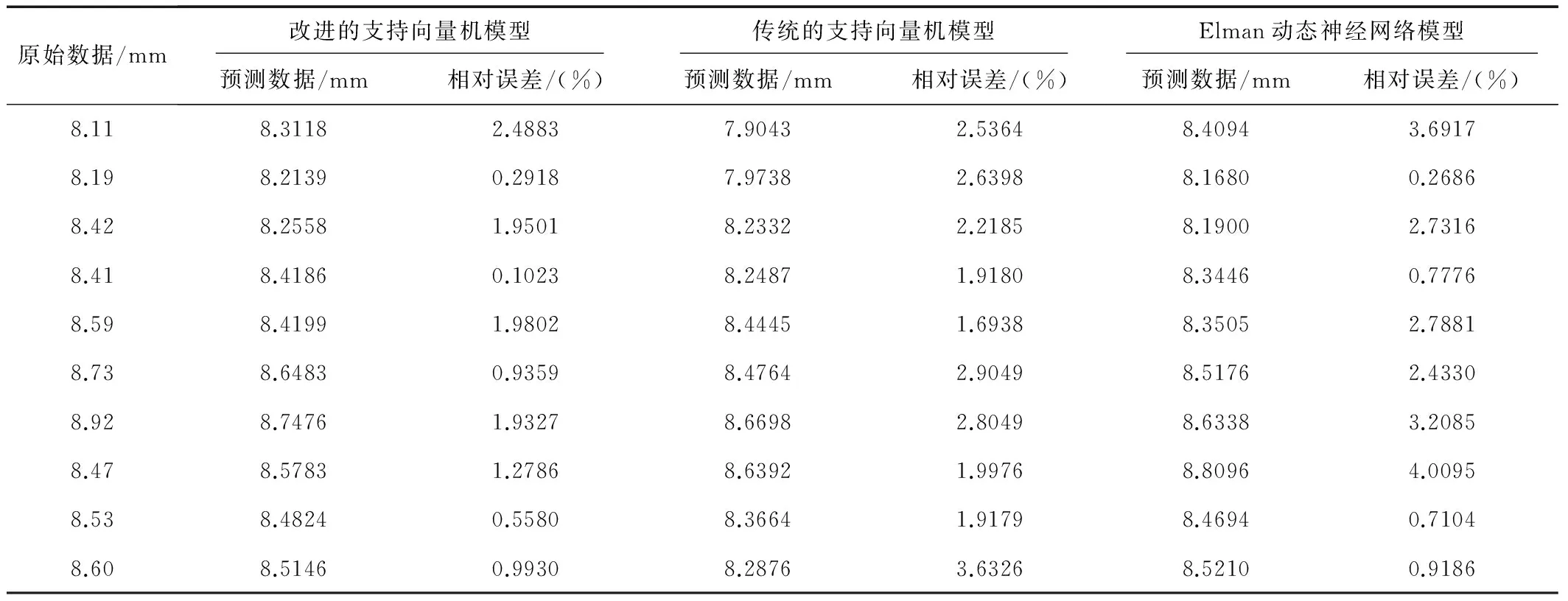
表3 原始数据与预测数据的对比Tab.3 Comparison between original and predicted data

为了更好的验证改进支持向量机预测模型的预测精度，本文再利用平方和误差SSE、平均相对误差MRE以及均方误差MSE这3种误差检验指标对预测集预测结果进行综合评价，结果见表4。

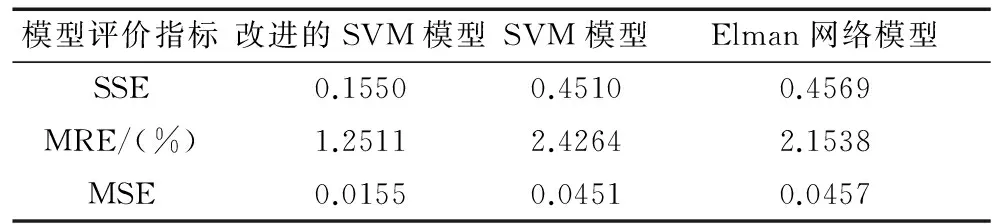
表4 CX6-6.5各模型预测结果综合评价Tab.4 The comprehensive evaluation of predicted results for CX6-6.5 in three models

通过各模型预测结果综合评价表4，比较平方和误差、平均相对误差以及均方误差的数值，然后综合表3比较结果，可以明显地得出：基于改进SVM模型的精度最高，各项检验指标都优于传统SVM模型以及Elman网络模型，稳定性较好。

7 结束语

利用PSO优选SVM模型的参数，得到了较优的改进SVM预测模型，改进SVM预测模型的预测精度各项误差指标都要优于传统SVM预测模型和Elman动态神经网络，具有更高的预测进度，避免了局部最优解，所以基于改进的SVM预测模型能更贴近深基坑系统的动态非线性特点，且不受样本数据大小的影响、泛化性能、稳定性、适应性均较好。证明了将粒子群优化算法和SVM理论相结合来用于深基坑变形预测是完全可行的，较好地验证了SVM模型的特点，且有较高的预测精度。

[1] 黄声享，尹晖，蒋征.变形监测数据处理[M].武汉：武汉大学出版社，2010.

[2] 吴庆令.南京地区基坑开挖的变形预警研究[D].南京：南京航空航天大学，2006.

[3] 高大钊.深基坑工程[M].第2版.北京：机械工业出版社，2002.

[4] Norwegian Public Roads Administration.Road Tannel[Z].Norwegian：Mpraprinting center，2004.

[5] 顾民.城市地下道路规划研究[D].上海：同济大学，2005.

[6] 何雄君，梁会，王建平，等.我国互通式立交变速车道长度的确定方法研究[J].武汉理工大学学报，2005，29(3)：370-373.

[7] 北京市市政设计研究院.CJJ 37—90 城市道路设计规范[S].北京：中国建筑工业出版社，1991.

[8] 张韬.深基坑变形预测模型研究及工程应用[D].长沙：中南大学，2009.

[9] 张学工.关于统计学习理论与支持向量机[J].自动化学报，2000，26(1)：32-42.

[10] He P，Wang Y，Gui W，et al.Chaotic time series analysis and SVM prediction of alumina silicon slag composition[C].Proceeding of Fourth International Conference，Beijing，China：2010，1273-1277.

[11] 方瑞明.支持向量机理论及其应用分析[M].北京：中国电力出版社，2007：47-49.

[12] 刘运荣.基于支持向量机的时间序列预测研究[D].哈尔滨：哈尔滨工程大学，2008.

[13] Baesens B，Viaene S，Gestel T Vetal.An empirical assessment of kernel type performance for least squares support vector machine classifiers[C].Proceeding of Fourth International Conference on Knowledge-Based Intelligent Engineering Systems and Allied Technologies，Brighton，UK2000：313-316.

[14] 纪震，廖惠连，吴青华.粒子群算法及应用[M].北京：科学出版社，2009.

[15] 王慧勤.基于支持向量机的短期风速预测方法[D].西安：西安科技大学，2009.

[16] 李丽，牛奔.粒子群优化算法[M].北京：冶金工业出版社，2010.

Deformation Prediction of Deep Foundation Pit Based on Improved Support Vector Machine

WU Huan1，ZHOU Chun-bo2，QIN Kun3

(1.JiangxiEnvironmentalEngineeringVocationalCollege，GanzhouJiangxi341000，China； 2.JiangxiInstituteofSoilandWaterConservation，NanchangJiangxi330029，China； 3.SurveyingandMappingBrigade，JiangxiProvincialCoalGeologyBureau，NanchangJiangxi330029，China)

Deep foundation pit deformation monitoring and prediction is an important link in the design and construction of the deep foundation pit.To accurately predict the deformation of the deep foundation pit in the future is the ultimate goal of the monitoring.In view of the traditional prediction method contains certain limitations，based on the current research situation of Support Vector Machine，the paper proposes a method of deformation prediction of deep foundation pit based on SVM to solve effectively such problems as small samples，nonlinear，high dimension and local minimum，etc.The method is as follows:firstly using the particle swarm algorithm to optimize the parameters of SVM，and then to obtains the improved SVM forecasting model，then compared with its prediction data and that of traditional SVM model and Elman dynamic neural network model，at last using the mean square error，the squares sum error，and the average relative error to evaluate the prediction effect.The experimental results show that the forecasting model based on improved SVM can better reflect the dynamic nonlinear characteristics of deep foundation pit system，and it has certain superiority and the engineering application promotion value.

deep foundation pit；deformation prediction；improved Support Vector Machine

2015-08-04

P 258

A

1007-9394(2015)04-0025-04

吴欢(1989～)，男，江西抚州人，硕士，讲师，工程师，现主要从事工程测量方面的教学工作。