异常值对非参数bootstrap法估计的影响分析

刘 薇，常振海

(天水师范学院 数学与统计学院，甘肃 天水 741001)

0 引言

若记 X=(X1，X2，…，Xn)为来自总体 F的样本,要估计的统计泛函为Tn=g(X),那么非参数bootstrap法[1]的思想可以描述为

因为bootstrap方法给每个样本点以同样的概率(均为1/n),因此,在样本中混入异常值时,其估计的效果如何并未见在文献中专门讨论过,本文讨论了这个问题。

1 方法步骤

为了能较好地进行分析,我们设计了如下的方法步骤,因为主要在小样本下进行探讨,所以文中固定样本容量n=20,总体分布为N(1.4，12)。

(1)产生容量为20的服从N(1.4，12)的样本,其一个样本的均值为=1.5161,标准差为σ=0.8774,这个均值将作为非参数bootstrap法的总体。

(2)生成含有单侧异常值的样本。

方法是产生容量为50的服从N(-5，12)的样本,去掉前后各20个值,保留中间的10个值,作为异常小值,用于逐个替换步骤(1)中的样本,得到5%、10%、20%、40%、50%等比例下的含有单侧异常小值情形的样本。

下面解释下为什么N(-5，12)的样本可以作为异常值。在正态分布中,由3σ 原则知,落于| x-μ |≤3σ 之外的x可能性仅有0.27%,我们产生一次样本,由实际推断原理,出现这样的x一般不可能,将被看做异常值。假设方差不变,从图1中能直观看出,这里产生的异常值是合理的。

从图1能看出,在方差相同(σ=1)情形下,μ1≤μ-6σ=1.4-6×1=-4.6 时,以分布 N(μ1，12)产生的点对分布N(1.4，12)的样本点来说是异常小值,所以本文中以N(-5，12)来产生异常小值是合理的。同理,以N(8，12)产生的点对分布N(1.4，12)的样本点来说是异常大值也是合理的。

(3)生成含有双侧异常值的样本。

方法是同时将步骤(2)中产生的异常小值和异常大值替换步骤(1)中的样本点,则得到10%、20%、40%、50%下的含有双侧异常值的样本。因为极小极大异常值各最少一个,故这种情形下含异常值比例最小为2/20=10%。

(4)在单侧和双侧异常值两种情形下,分别计算总体均值的非参数bootstrap法点估计、分布形态、区间估计等。

(5)在相应的评判标准下,进行比较分析。

2 模拟分析

序列中混入异常值一般有三种情形：混入异常小值、混入异常大值和同时混入异常小值和异常大值。鉴于单侧异常小值和单侧异常大值的类似性,下面仅从混入异常小值，同时混入异常小值和异常大值两个方面进行讨论。

赛事组织者与传播者之间的博弈与第一个博弈的结果密切相关：赛事组织者希望通过集中行使体育赛事转播权以提高自己的议价权，而传播者则希望存在多个议价对象，以便降低自己的传播成本。这一博弈主要引发了前文所提到的垄断问题：由赛事组织者统一行使体育赛事转播权是否构成垄断；将体育赛事转播权授予一个传播者专有又是否构成垄断。

2.1 单侧异常值对bootstrap法估计的影响分析

主要考察异常小值的影响，异常大值的类似，不再重复讨论。

(1)对点估计的影响。

表1 异常小值对样本均值非参数bootstrap法估计的影响

从表1能看出,在没有加入异常小值时,样本均值的非参数bootstrap法估计为1.5159,与样本均值1.5161几乎相等,但加入异常值后,bootstrap法估计就与样本均值相差较大,且随着异常值比例的增高,它们相差也越来越大,这点从绝对误差和相对误差数值上能很好的反映出来,这两者的值均逐渐增大,说明点估计距离真值渐远。从稳定性(标准差和CV)方面看,随着异常小值比例的提高,bootstrap法估计的稳定性逐渐变差,不过在异常小值的比例为50%时,波动稳定性又有点提高。

(2)对点估计分布形态的影响。

对B=3000个bootstrap法估计,绘制其直方图,同时考察反映分布形态的参数偏度和峰度,结果见图2。

图2 异常小值各比例下bootstrap法估计的直方图

从图2能看出,在没有异常小值的情形下,均值的bootstrap法估计很接近于正态分布,但在5%比例的异常小值影响下,分布的偏度和峰度都发生较大的变化,随着异常小值比例的增加,分布又回复到接近正态分布。说明异常小值的比例越低,对分布形态的影响越大。

(3)对区间估计的影响。

从图2中看到,尽管在异常小值比例较高的情形下,bootstrap法估计的分布形态接近于正态分布,但因其点估计与总体真值相差较大,故其区间估计不一定好。采用性质较好的BCa区间[8],bootstrap法估计结果见图3,每个比例下的区间均进行100次估计,为了能较清楚地显示,这里仅显示了前20个区间估计。

图3 异常小值各比例下bootstrap法区间估计

从图3能看出,没有异常值的bootstrap法区间估计几乎对称,但加入了5%比例的异常小值后,区间估计的上下限均不同程度地变小了,在10%比例情形下,变小的趋势进一步加剧,区间估计几乎覆盖不住真值了,而到了20%比例时,区间估计竟没一个能覆盖真值的,说明随着异常小值比例的增加,区间估计变得越来越不好。各个比例下100区间估计的上下限及区间长度平均值见表2。

表2 异常小值对样本均值bootstrap法区间估计的影响

从表2能看出,不仅在图3中反映的上下限随异常小值比例的增加逐渐减小的现象,并且区间的长度也越来越长,这都说明异常小值对区间估计的影响是非常不好的。

2.2 双侧异常值对bootstrap法估计的影响分析

(1)对点估计的影响。

在样本容量为20时,同时存在异常小值和异常大值,最少需要两个异常值,故考虑的最小异常值比例为2/20=10%,结果见表3。

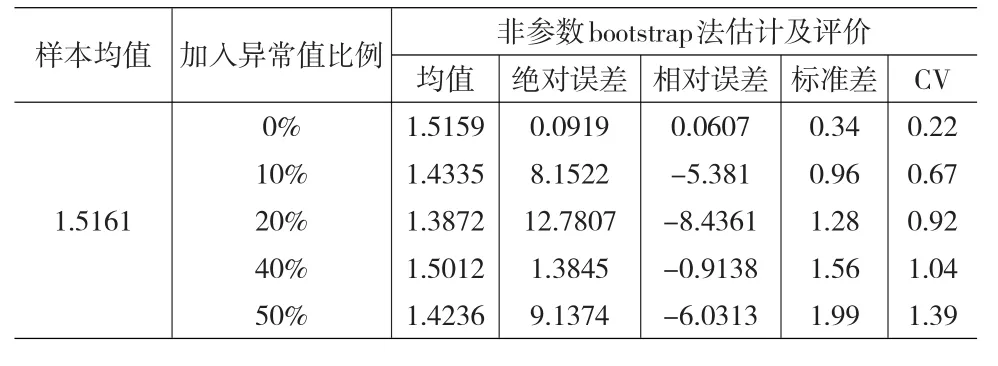
表3 双侧异常值对样本均值bootstrap法估计的影响

从表3能看出,和没有异常值相比,样本中混入了异常值后其估计的绝对误差和相对误差均明显偏大,并且相对误差均为负值,说明同时存在异常小值和异常大值的情形下,异常小值的影响更大些。从标准差和CV值上能看出,样本中加入了异常值后,稳定性逐渐变差。

如果将表3和表1相比,从相对误差的角度看,双侧异常值对bootstrap法点估计的影响比单侧的影响要小。

(2)对点估计分布形态的影响。

类似于单侧异常值情形,仍然计算B=3000个bootstrap法估计,绘制其直方图,同时考察反映分布形态的参数偏度和峰度,结果见图4。

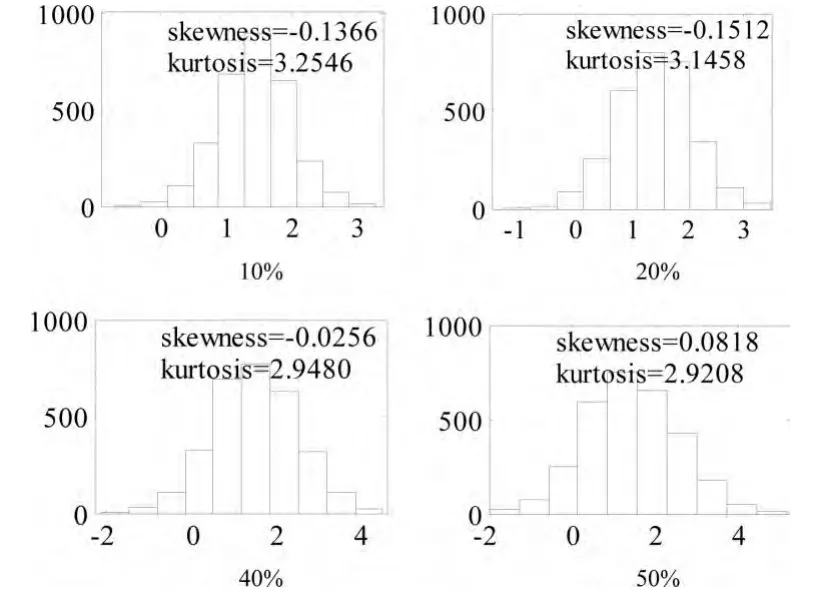
图4 异常小值各比例下bootstrap法估计的直方图

从图4能看出,这些估计的分布均近似于正态分布,这一点和单侧异常值情形不是很类似。分布形态的近似对称性将对区间估计的覆盖率很有好处,下面讨论这个问题。

(3)对区间估计的影响。

对各个异常值比例下的情形均计算了100个BCa区间,图5显示了前20个。

图5 双侧异常值各比例下bootstrap法区间估计

从图5能看出,各个比例情形下的区间估计覆盖率均为1,说明覆盖率比单侧异常值情形下好。100个区间估计的上下限及长度的平均值见表4。

表4 双侧异常值对样本均值bootstrap法区间估计的影响

从表4能看出,随着异常值比例的增加,区间的长度逐渐变长,甚至比单侧情形下的还要长,说明好的覆盖率是以牺牲区间长度为代价的,应该说区间估计并不好。

3 结论

综合上面单侧和双侧情形下模拟分析,我们可以得到下面的结论。

(1)在点估计方面,比较表1和表3,同样的异常值比例下,显然单侧异常值要比双侧异常值影响大;不同的异常值比例下,随着比例的增加,点估计逐渐变差,距离真值越来越远。

(2)在点估计的分布形态上,比较图2和图3,在同样的异常值比例下,单侧异常值的直方图比双侧异常值的左偏多一些,峰度则相差不是很大。不同的异常值比例下,随着比例的增加,分布均接近于正态分布,说明异常值的比例越低,对分布形态的影响越大。

(3)在区间估计上,双侧异常值情形下均能覆盖真值,但区间长度较长;单侧异常值情形下,在异常值比例较低时能覆盖真值,但比例增高时,区间估计就不能再覆盖真值,不过相比于双侧情形,区间估计长度短。

[1]Efron B,Tibshirani R J.An Introduction to The Bootstrap[M].New York:Chapman&Hall Ltd,1993.

[2]Hall P,Horowitz J.A Simple Bootstrap Method for Constructing Nonparametric Confidence Bands for Functions[J].The Annals of Statistics,2013,41(4).

[3]Fay M P,Brittain E H,Proschan M A.Pointwise Confidence Intervals for A Survival Distribution With Small Samples or Heavy Censoring Biostat[J].Biostatistics,2013,14(4).

[4]Thai1 H T,Mentré1 F,Holford N H G.A Comparison of Bootstrap Approaches forEstimating Uncertainty ofParametersIn Linear Mixed-effects Models[J].Pharmaceutical Statistics,2013,12(3).

[5]黎光明，张敏强.概化理论方差分量置信区间估计方法的比较[J].统计与决策,2013,(9).

[6]Romano J P,Shaikh A M.On The Uniform Asymptotic Validity of Subsampling and The Bootstrap[J].The Annals of Statistics,2012,40(6).

[7]DiCiccio J,Efron B.Bootstrap Confidence Intervals[J].Statistical Science,1996,11(3).