变分法应用条件的探索及其灵敏度分析

翁云华，杜　娟，王雪娇（成都理工大学管理科学学院，四川成都610059）

变分法应用条件的探索及其灵敏度分析

翁云华，杜娟，王雪娇
（成都理工大学管理科学学院，四川成都610059）

考虑和探究变分法中的各种条件，通过对极值必要条件的探索和对不固定的自然条件的端点进行分类讨论，以及对横截性条件的端点问题进行探究，最终得到对变分法应用条件的总结以及各种情形的分析讨论，使得变分法可以更好地拓展和运用到许多实际问题中.在此基础上对变分法的各类讨论情形进行了灵敏度分析，考察当参数变化时，原目标函数的最优解变化情况，以及变化率的高低，推导并得出可直接求变分法的灵敏度的公式.由此简化了获取灵敏度的难度，及复杂性，并将所得的灵敏度公式应用于实践.

欧拉拉格朗日方程；自然横截性条件；变分法；横截性条件；灵敏度分析

Weng YH,Du J,Wang XJ.The Exploration of the Condition of Variation Method and Sensityvity[J].Journal of Yibin University,2015,15（6）：117-120.

变分法是17世纪末叶开始发展起来的一个数学分支，它是为了解决实践问题中的极值问题而产生的.不过它所讨论的不是求普通函数的极值，而是泛函的极值问题.近年来，对变分问题各类条件的探索已经成为人们研究的热点.由老大中编写的《变分法基础》一书中对变分法的4类应用条件作了详细的描述和总结.本文在此基础上，考虑变分的每一个变量都与参数p有关，观察当参数改变时，目标函数相应的最优解的变化，推导出直接计算目标函数灵敏度的公式.主要意义在于，对给定的目标函数，可以直接利用公式计算其灵敏度，从而大大减小了计算量，节约了计算成本.

1　准备知识

问题[1]：设函数F（x）在[a,b]上连续，任意函数u（x）在区间[a,b]上具有n阶连续导数，考虑变分法在约束条件下的极值问题（泛函求极值问题）

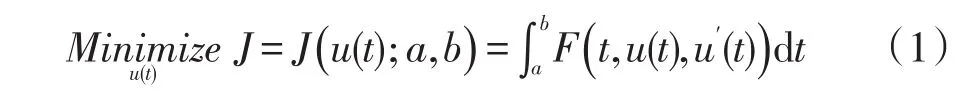
约束条件为向量

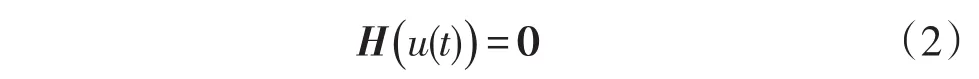
其中向量

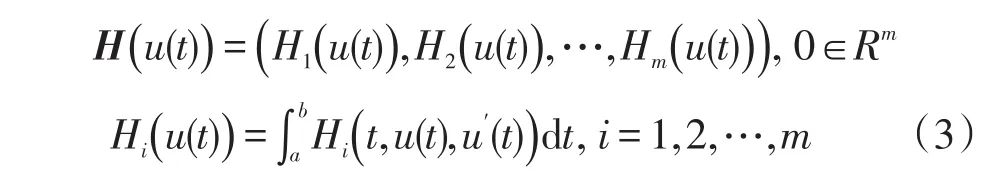
为了分析这个问题的平衡条件（目标函数取得极值时的条件），定义函数关于其参数变分，函数J与参数u,a,b有关.变分δJ定义为：

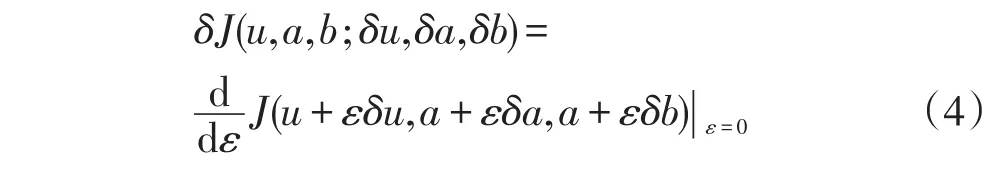
2　条件探索

定理1[2]若J和H定义如上，设u*（t）为问题（1）-（2）的局部极值，设集合G={u（t）|：H（u（t））=0}非空，并且设J,H在u*的一个领域内，J和Hi是弱连续的.如果对于G中的任一函数u（x）都有 δJ= ΔJ=J[u（x）]-J[u*（x）]=0，则泛函J[u（x）]在u*（x）出取得极值.

极值必要条件[3]：下述条件（I）和条件（II）必有一个成立.

条件（I）：对于所有增量 δu1,…,δum和增量δH1,…,δHm有：

条件（II）：对于u,a,b的任意增量δu,δa,δb，存在常数使得

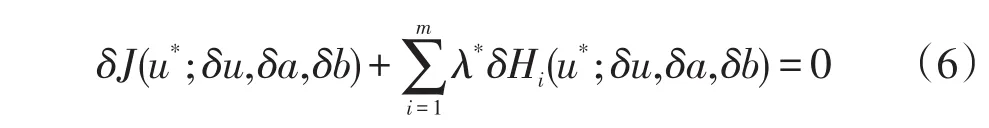
若（5）不成立，则（6）可化为

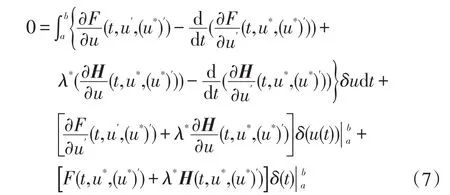
其中 δu（t）、δa、δb为u（t）、a、b各自的增量，λ*= （…,），H=（H1,…,Hm），δa=δ（t）|a.

以上等式要求F和H对u和u′的偏导数存在.在下面的讨论中，假设所有涉及到的函数充分光滑，在实际应用中通常会遇到以下四种情形：

情形1[4]：由于δu的任意性（7）式可化简为满足极值条件的欧拉－拉格朗日方程：

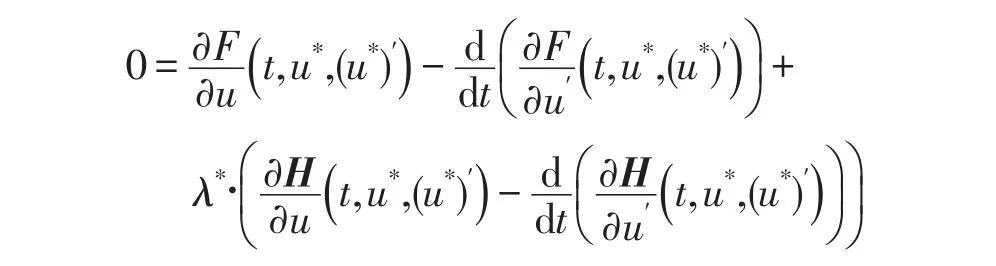
把这样定义的泛函变分是由拉格朗日泛函变分法得到的，称之为拉格朗日泛函变分，它与前面定义的变分是等价的，而且也便于计算泛函的变分.

为方便书写，引进符号：

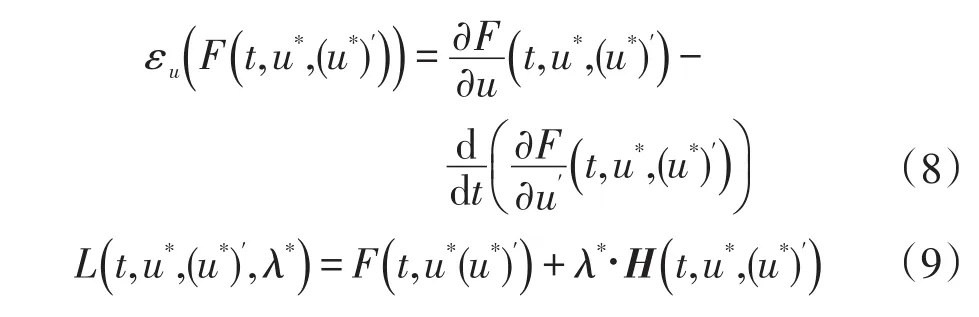
所以欧拉－拉格朗日方程可简记为：

情形2：如果u（a）或u（b）非定值，由δu（a）的任意性，可将（7）式化简得到关于u的边值不固定的自然边界条件：

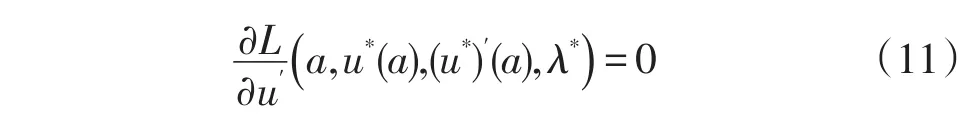
例1[5]：求泛函J[y]=[p（x）y′2+q（x）y2+2f（x）y]d x极值问题的自然边界条件，其中x0和x1均为自由边界，p（x）,q（x）和 f（x）均为已知函数，且p（x）≠0.

解：因为x0和x1均为自由边界，根据定理1及情形1、2的自然边界条件为

情形3：如果端点a或b为自由端点.则自由端点a或b满足泛函求驻值的必要条件，这种条件称之为端点不固定自然边界条件，同时把固定边边界条件称之为强制边界条件或本质边界条件，由于δ（a）或δ（b）的任意性，有：

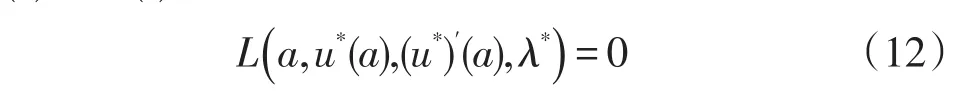
情形4[6]：如果右端点固定，而端点a在曲线Ψ（t）上滑动，由y=u（x）与已知曲线y=Ψ（x）交点处的u′与Ψ′的斜率关系，有横截性条件（斜截条件）：

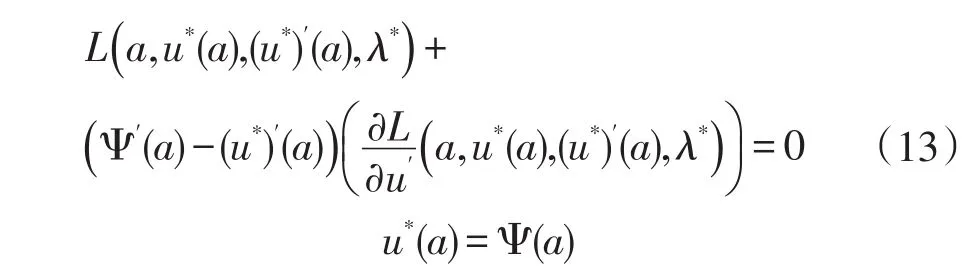
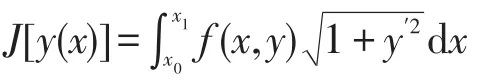
解：由以上横截性条件可得：

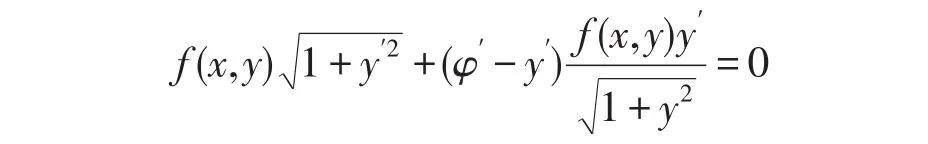
化简得：

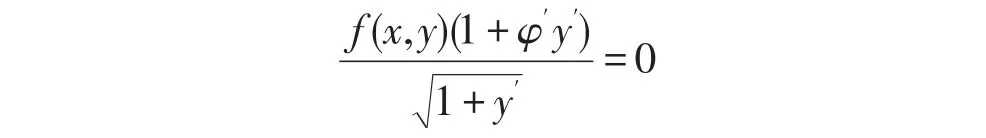
3　灵敏度分析

考虑带参数组的变分问题，分析当参数变化时相应的最优解的变化，为了方便起见，首先考虑有限个参数的情形，考虑问题[8]

约束条件为

其中

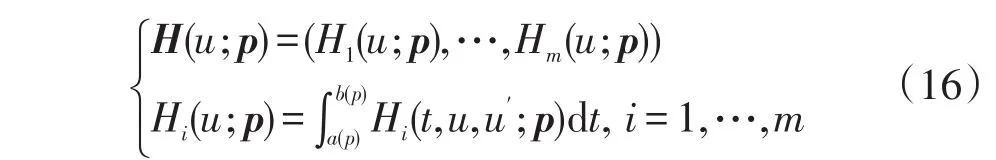
且0∈Rm,p=（p1,…,pm）∈Rk是参数向量.

这个问题能够取到最优解u*的必要条件已经通过欧拉拉格朗日方程（10）给出，现在假设约束条件（15）以及依赖于这个问题的等式（11）-（13）都与参数p有关.

为获得方程组的灵敏度，计算所有参数的变分.由（14）和（16）得（17）：

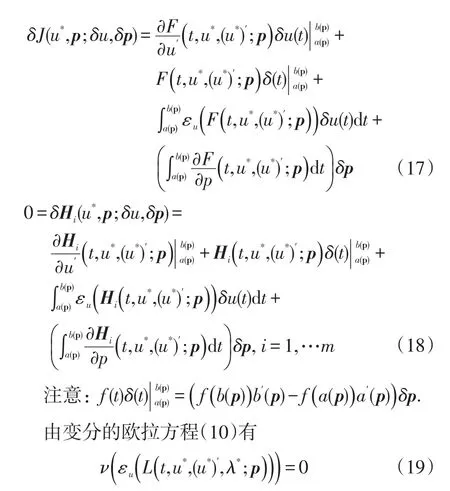
其中算子ν定义如下：

如果边界是固定的，由变分的边界条件得

在端点a处如果u（a）是不固定的，则有变分自然横截性条件[9]：

同样地，如果a是不固定的，则有变分的自然边界条件为：

如果在端点a处，若端点在曲线ϕ（t；p）（对比（13）式）上滑动，有变分的横截性条件：

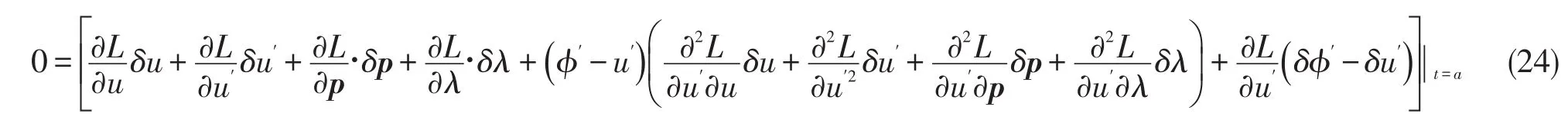
其中：

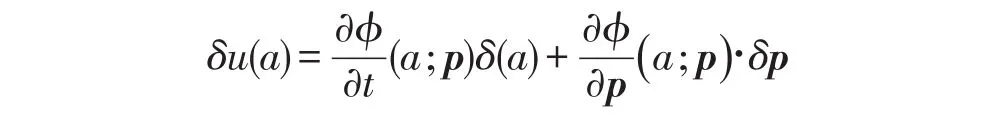
对于每一个λ,p,δλ,δp都在一个非齐次线性二阶积分方程中，和（24）一起构成边值问题，它的解结合（17）、（18）可获得关于J,u,λ及其相应的灵敏度.通常用单位矩阵来代替δp.需要注意的是（17）、（18）、（24）给出了关于δJ,δp,δλ的线性方程组.

所以原问题（14）-（16）的目标函数的关于参数p的灵敏度向量可给出如下：

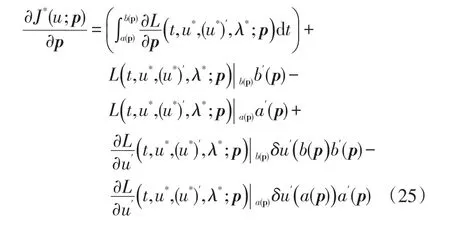
这是关于参数 p的拉格朗日函数在最优解u*,λ*处的梯度.

虽然原问题和双变量的灵敏度很难获得，以上实际结论却为提供了计算灵敏度的直接公式.

对于有无限个参数的目标函数的灵敏度也可以类似得到.下面简单看一下求灵敏度的实际应用

例3：考虑下面关于参数p的问题

约束条件为

由于已经给出灵敏度的公式，所以可以直接进行计算.

为了计算J,λ,u（t；p）的偏导数，首先解决关于p的参数问题，问题的欧拉方程为：

其解为：

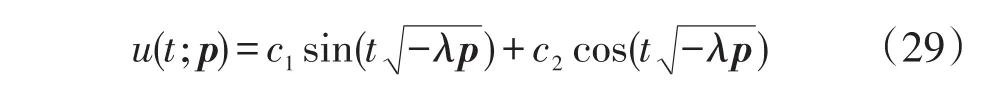
在（29）中应用边界条件，得到最优解

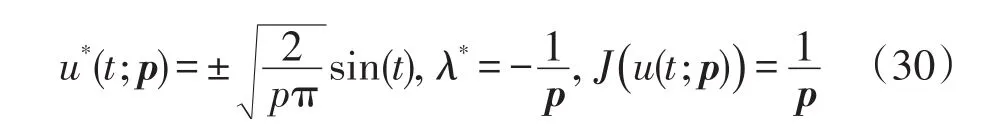
则u（t,p）,λ,J的偏导数为

由此便得到了目标函数的灵敏度.

4　结语

方程（10）-（13）是变分法求极值的著名的必要条件，对泛函求极值提供了事半功倍的作用.在自然科学和工程技术中所遇到的变分问题，有时要求极值函数除满足给定的边界条件外，还要满足一定的附约束加条件，这些附加条件也可直接在变分法的应用条件基础上再上附加条件，就可以直接应用各类条件即可，这就是泛函的求条件极值问题.泛函的条件极值的计算方法与函数的条件极值的计算方法类似，很多问题也可用拉格朗日乘数法来实现.

变分方法已经被越来越多的拓展和运用到许多实际问题中.（25）式给出了目标函数直接求灵敏度的公式，为在应用实践中求灵敏度提供了很大的方便，同时对于变分法的灵敏度分析方法也可适用于（线性和非线性）最优化问题，以及优化控制问题，其灵敏度的获取方法与求变分法的灵敏度相似.

[1]Bonnans JF,Shapiro A.Perturbation analysis ofoptimization prob⁃lems[M].NW：Springer,2000.

[2]Caillau JB,Noailles J.Sensitivity analysis for time optimal orbit transfer[J].Optimization：A Journal of Mathematical Programming and OperationsResearch,2001,49（4）：327-350.

[3]Castillo E,Conejo A,Pedregal P,etal.Building and solvingmathe⁃matical programming models in engineering and science[M].Pure ApplMath,2001.

[4]Conejo A,Castillo E,Mínguez R,et al.Decomposition techniques inmathematical programming engineering and science applications [M].NW：Springer,2011.

[5]Gelfand IM,Fomin SV.Calculus of Variations[M].NJ：Englewood Cliffs,1963.

[6]老大中.变分法基础[M].北京：国防工业出版社,2004.

[7]Castillo E,Conejo A J,Castillo C,et al.Perturbation approach to sensitivity analysis inmathematical programming[J].JOptim Theo⁃ry and Applications,（2006）[2015-02-14].http：//citeseerx.ist.psu.edu/viewdoc/summary？doi=10.1.1.378.3590.

[8]Castillo E,Conejo A,Castillo C.A closed formula for localsensitivi⁃ty analysis inmathematical programming[J].Engineering Optimiza⁃tion,2006（38）：93-112.

[9]Gal T,Greenberg H J.Advances in sensitivity analysis and para⁃metric programming[M].NW：Springer,1997.

（编校：许洁）

The Exploration of the Condition of Variation Method and Sensitivity Analysis

WENGYunhua,DU Juan,WANGXuejiao
（College ofManagementScience,Chengdu University ofTechnology,Chengdu,Sichuan 610059,China）

The various conditionsofvariationalmethod wasexplored through theexploration ofnecessary conditionsofex⁃treme and classified discussion on the endpoints of unfixed natural conditions.Endpoint issues of transversality condi⁃tionswere explored so as to eventually get the summary ofapplication conditions of variationalmethod,ensuring the bet⁃ter developmentand further application of variationalmethod in solving practical problems.Sensitivity analysiswere then carried outon the basis of the above research of variationalmethod to observe the shiftof optimal solution of original ob⁃jective function with parameters change,aswellas the rate of change.And a formula of directly getting the sensitivity rate ofvariationalmethod were derived.Thissimplifies complexity in accessing sensitivity issues.

Euler-Lagrange equations；natural and transversality conditions；calculus of variations；transversality condi⁃tions；sensitivity analysis

O29

A

1671-5365（2015）06-00117-04

2015-03-24修回：2015-04-08

翁云华（1991-），男，硕士研究生，研究方向为应用泛函分析

网络出版时间：2015-04-09 09：59网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20150409.0959.001.html

引用格式：翁云华，杜娟，王雪娇.变分法应用条件的探索及其灵敏度分析[J].宜宾学院学报,2015,15（6）：117-120.