一类分数阶微分方程的解及其应用

张　静，雍丹丹，眭方微（成都理工大学管理科学学院，四川成都610059）

一类分数阶微分方程的解及其应用

张静，雍丹丹，眭方微
（成都理工大学管理科学学院，四川成都610059）

通过应用分数阶导数的拉普拉斯变换和二项式展开系数，得出一类常系数齐次分数阶微分方程的精确解，实例展示了这一结果的有效性.

分数阶微分方程；Laplace变换；解析解

Zhang J,Yong DD,SuiFW.The Solution ofa Classof FractionalDifferential Equationsand its Applications[J].Journal of Yibin University,2015,15（6）：113-116.

分数阶微分方程具有深刻的物理学背景和丰富的理论内涵，顾名思义分数阶微分方程就是指含有非整数阶导数的方程.目前，分数阶导数和分数阶积分在物理、机械工程和控制理论等领域发挥越来越重要的作用，如有混沌动力行为的动力系统、拟混沌动力系统、复杂物质或者多孔介质的动力学、具有记忆的随机游走等.与整数阶微分方程相比，分数阶微分方程能更好地描述某些自然物理现象和动态系统过程.随着分数阶微积分的广泛应用，越来越多的学者对其有着极大的关注.

1　基本定义

定义函数 f（x）的分数阶导数为[1-2]：

函数 f（x）（0＜x＜∞）的Laplace变换：

由此不难得出[3]：

二项式系数定义为[4]：

其中n,k都是整数.0!=1

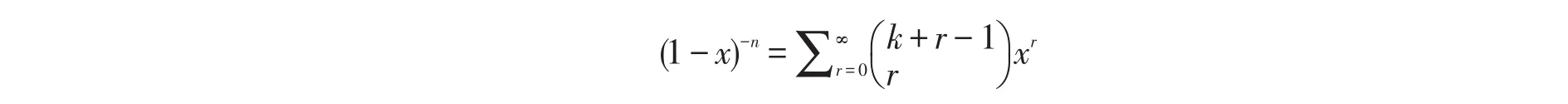
Mittag-Leffler函数的定义为[5]：

2　分数阶微分方程的解

通过应用Laplace变换研究：

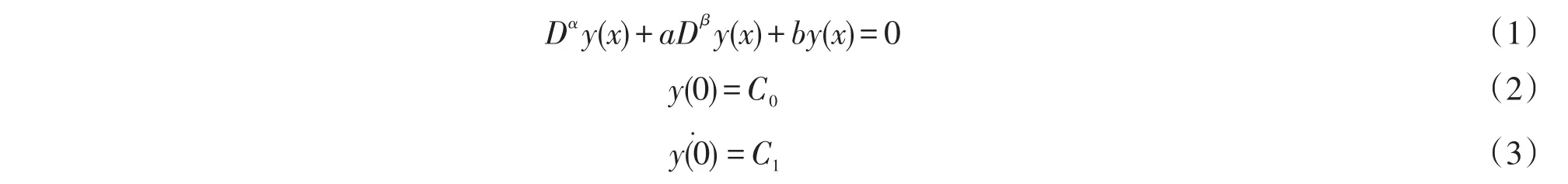
的解析解，其中α∈（1,2）,β∈（1,2）,a,b∈ℝ.

定理1若α∈[1,2],β∈[1,2],a,b∈ℝ，当α、β不同时为整数则定解问题（1）、（2）、（3）的解为：

证明：由定义2对方程（1）进行Laplace变换：

注记：①当α、β同时为整数时，则方程（1）就是通常意义下的常系数常微分方程.

②方程（1）中，当a=0时有：

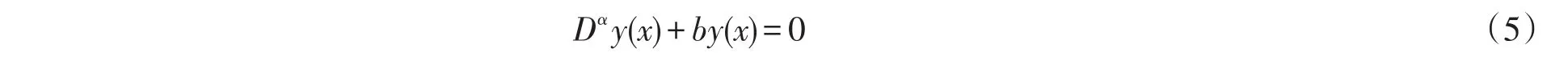
定解问题（2）、（3）、（5）的解为：

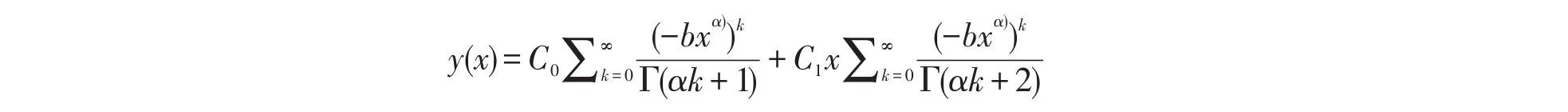
定理2若α∈[0,1],β∈[0,1],a,b∈ℝ,当α、β不同时为整数,则下列定解问题

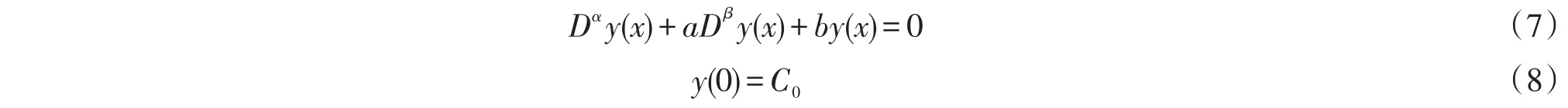
的解为：

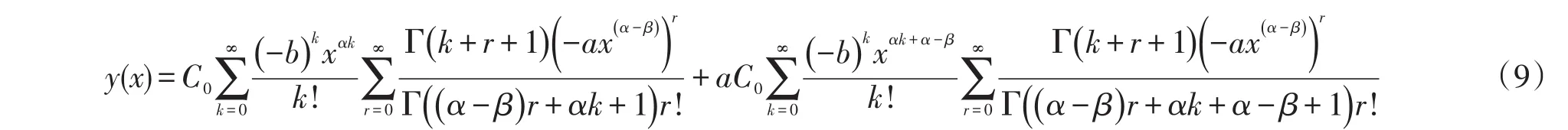
证明：对（7）进行Laplace变换得：

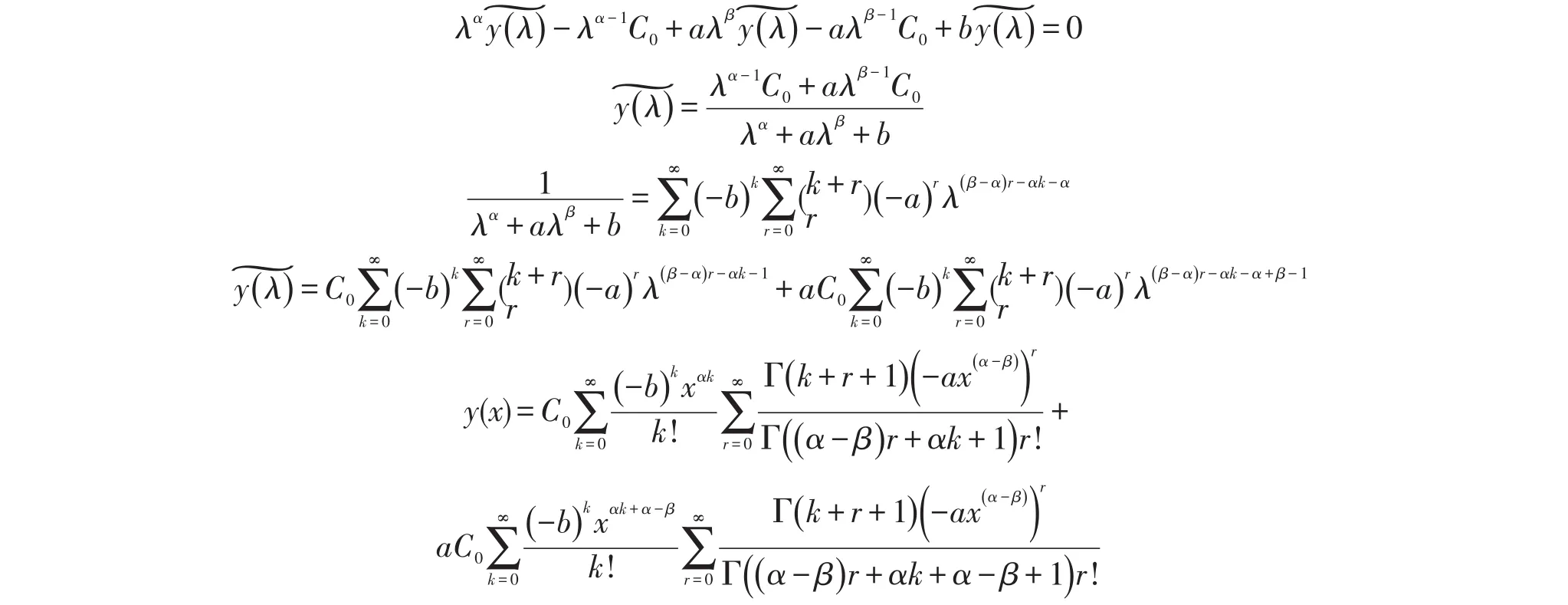
注记：③当α、β同时为整数时，则方程（7）就是通常意义下的常系数常微分方程.

④方程（7）中，当a=0时有：

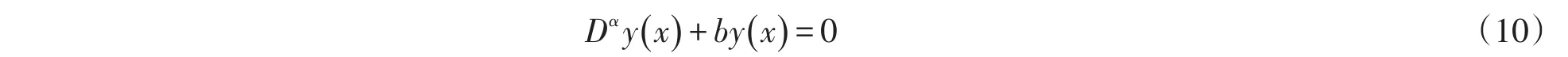
定解问题（8）、（10）的解为：

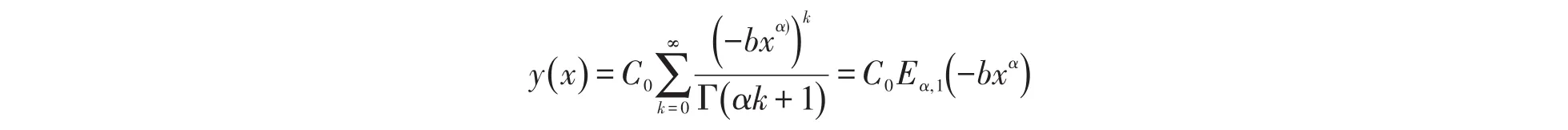
3　计算实例

例1：广义的粘性自由阻尼振荡分数阶微分方程[6]

例2：解下列分数阶微分方程：

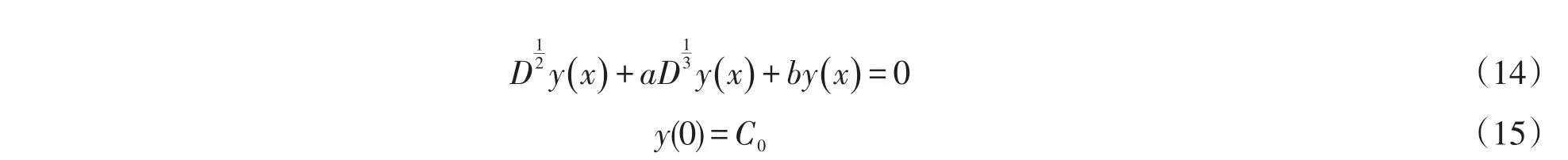
例3：求解下列简谐波方程[7].

解：①当α∈（1,2]时，由注记2可得问题（16）、（17）、（18）的解为y（x）=C0Eα,1（-bxα）+C1xEα,2（-bxα）.

②当α∈（0,1]时，由注记4可得问题（16）、（17）、（18）的解为y（x）=C0Eα,1（-bxα）.

4　结论

本文通过应用Laplace变换讨论得出了两类常系数分数阶微分方程的解析解，通过实例对文章结果的应用说明了要求解该类分数阶微分方程的精确解，可以直接采用定理1和定理2的结论.

[1]KilbasAA,Srivastava HM,Trujillo JJ.Theory and applicationsof fractionaldifferentialequations[J].Elsevier,Amsterdam（2006）：236-240.

[2]MainardiF.The fundamentalsolutions for the fractionaldiffusion-waveequation[J].ApplMath Lett,1996：23-28.

[3]郭柏灵,蒲学科,黄凤辉.分数阶偏微分方程及其数值解[M].北京：科学出版社,2011.

[4]陈纪修,於崇华,金路.数学分析[M].北京：高等教育出版社,2009.

[5]Vladimir V.Uchaikin.FractionalDerivatives for Physicistsand Engineers[M].Beingjing：Higher Education Press,2013.

[6]Gorenflo,R,Mainardi,F,Srivastava,HM.Special functions in fractional relaxation-oscillation and fractionaldiffusion-wave phenomena[C]//ainov D.Proceedingsof the Eighth InternationalColloquium on DifferentialEquations,Utrecht：VSPPublishers,1998：217-234.

[7]Lin SD,Lu C H.Laplace transform for solving some families of fractional differential equations and its applications[J].Advances in Difference Equations,2013：108-113.

（编校：许洁）

The Solution of a Class of Fractional Differential Equations and its App lications

ZHANG Jing,YONGDandan,SUIFangwei
（College ofAdministrative Science,Chengdu University ofTechnology,Chengdu,Sichuan 610059,China）

By using the fractional derivative of the Laplace transform and binomial expansion coefficient,the homoge⁃neous fractionaldifferentialequationswith constantcoefficientsofa classofexactsolutionswasobtained.Example shows the validity of the results.

fractionaldifferentialequation；Laplace transform；exactsolution

O177.91

A

1671-5365（2015）06-00113-04

2014-12-12修回：2014-12-30

张静（1989-），女，硕士研究生，研究方向为应用泛函分析

网络出版时间：2015-01-07 13：24网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20150107.1324.001.html

引用格式：张静，雍丹丹，眭方微.一类分数阶微分方程的解及其应用[J].宜宾学院学报,2015,15（6）：113-116.