粗糙集层次分析法在学生综合评价中的应用

卢　鹏，吴建乐（.西南交通大学峨眉校区基础课部，四川峨眉640；.西南交通大学数学学院，四川成都6003）

粗糙集层次分析法在学生综合评价中的应用

卢鹏1，吴建乐2
（1.西南交通大学峨眉校区基础课部，四川峨眉614202；2.西南交通大学数学学院，四川成都610031）

在对学生成绩综合评价中引入粗糙集理论和层次分析理论.利用粗糙集理论特有的属性约简和属性重要度原理能对有限的指标数据进行有效挖掘，具有客观性；而层次分析理论则从主观上进行补充，两种方法的结合能优化综合评价过程.通过实例分析，证实了该方法的可行性和有效性.

粗糙集理论；层次分析；学生综合评价；属性约简

Lu P,Wu JL.Application ofRough Setof Analytic Hierarchy Process in the Comprehensive Evaluation of Students[J].Journalof Yibin University,2015,15（6）：103-107.

随着经济、科学和技术的飞速发展，社会对人才的综合素质提出了更高的要求.大学生综合素质的培养已纳入高等教育的改革中，对学生的综合评价工作也是学校的重要工作内容之一.目前已有诸如主成分分析、聚类分析、数据包络分析、TOPSIS方法、灰色关联分析法、秩和比综合评价法、模糊综合评价等多种综合评价方法[1-3]，但这些方法都有其各自的局限性[4]，有时会出现模棱两可的评判结果（即多峰值），因此如何用科学的方法建立起学生综合素质的评价体系，一直是科研教育人员探索和关注的问题.本文基于对学生综合素质的特点，采用粗糙集评价法从客观方面进行属性约简，得到客观意义下的属性权重，然后再考虑各属性的实际意义，采用层次分析评价法得到主观意义下的属性权重，最后综合两种因素对学生进行合理评判，使结果更为准确，即避免了某些数据特殊造成的评价失真，又避免了人为原因造成的结果有误.

1　粗糙集基本理论[5]

粗糙集（Rough Set）理论[6]是数学家Pawlak在20世纪80年代初提出的.它建立在某个分类机制的基础之上，把分类看成特定空间上的等价关系，而该关系构成了对该空间的划分，空间中的一簇划分就是一个知识库.其主要思想就是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则.目前，该理论已被成功地应用于决策分析、模式识别、机械学习、数学挖掘与过程控制等领域.

1.1近似集[7]

设U是由感兴趣的对象组成的有限集合，称为论域，R是定义在U上的一个等价关系，U R表示其相应的分类，[x]R表示x所在的等价类，U的子集X称为概念，对于每个概念X可定义两个子集如下：

={x∈U|[x]R⊆U}

={x∈U|[x]R⋂U≠∅}

1.2信息系统

四元数组 S=（U,A,V,f）一个信息系统，其中U={u1,u2,…,u||U}是有限非空集；U中的元素称为对象；A={a1,a2,…,a||A}为属性的非空有限集合；f：U× A→V是一个信息函数，且∀x∈U,a∈A,f（x,a）∈Va.每个信息系统都可用一个信息表进行表示，当系统中没有重复元组时，此信息表就是一个关系数据库.

当 A=C⋃D,C⋂D=∅ 时，则称信息系统（U,A,V,f）为一个决策表.其中C与D中的属性分别称为条件属性和决策属性.

1.3属性约简

所谓信息系统的属性约简，就是在保持分类能力不变的前提下，按照一定原则，通过知识约简删除其中不重要或者不相关的属性，找到最小属性集确定的分类知识，这样便深化了对知识的认识.

设四元组S=（U,A,V,f）是一个信息系统，其中A为一簇等价关系，属性a∈A，假如满足ind（A-{a}）= ind（A），则称a为A中是不必要的；不满足则称a为A中是必要的.假如所有的a∈A都为A中必要的，则称A为独立的；否则称A为依赖的.对于依赖的属性集，其中必包含多余属性，可对其约简.

若B⊆A,B是独立的，且ind（B）=ind（A），则称B 是A的一个约简.A所有约简的交集称为A的核.

1.4属性的重要性

四元数组S=（U,A,V,f）是一个决策表，其中C与D分别称为条件、决策属性集.属性子集a∈C关于D重要性定义为：

其中|U|代表集合U的基数，σCD（a）越大说明属性a重要性高，反之重要性低.

2　层次分析法理论[8]

层次分析法是美国匹兹堡大学运筹学家Saaty 在20世纪70年代初提出的.它是一种定性分析与定量分析相结合的多目标决策分析方法.它是通过明确问题，建立层次结构，构造判定矩阵，层次单排序，层次总排序，一致性检验六个步骤来进行整个系统层次分析.

本文主要用层次分析理论进行属性的主观定权，通过检验后，再结合粗糙集方法得到的客观权进行组合，从而对学生进行综合评价.

3　粗糙集层次分析综合评价法流程

3.1评价信息系统的建立

从指标体系中找出最低一层指标，用来构成信息系统的属性集合，而评价的对象作为信息系统的对象集合，就可以建立起一个由所有对象和各指标值的信息系统.

3.2离散化指标数据

粗糙集方法只能处理离散化的数据，所以在评价中对每一个最低一层指标属性的评价结果用“1”“2”和“3”三个等级来衡量，并且根据实际情况分别用相应的数值来代替.当然在分级时也可用其它的离散化方法.

3.3信息系统属性约简

根据粗糙集属性约简原理进行属性约简，从指标体系中删除多余的属性，保留必要的属性，形成一个新的最小约简指标体系.粗糙集属性约简的算法有很多，有基于互信息的属性约简算法、区分矩阵约简算法、归纳属性约简算法、基于互信息的属性约简算法、基于搜索策略的属性约简算法和数据分析约简算法等[9].其中，以区分矩阵的约简算法[10]最有效率.本文利用区分矩阵来表达知识，在其基础上构造区分函数，运用吸收率[11]化简区分函数，最终得到约简后的属性集.

3.4粗糙集方法确定指标的客观权重

设S=（U,A,V,f）是一个信息系统，对化简后的A={a1,a2,…,am}，属性 ai在中的重要性为σCD（ai），则ai的权重定义为：

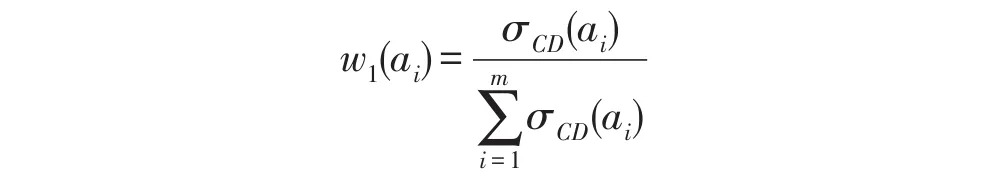
3.5层次分析法确定指标的主观权重

由粗糙集方法得到的信息系统约简后的属性集，再根据以往专家对各属性的之间的比较，建立各因素之间的成对比较阵A.

3.6综合评价合成

把主客观权重进行组合，可得：

其中α,β根据决策者对w1,w2的偏好程度进行调节.

利用上述结果，本文运用线性加权法进行计算：

其中：w（ai）为ai的组合权重；u（ai）为ai处理后的指标值；S为综合评价得分.

4　应用实例

表1是某学院抽取15名大四学生的综合成绩建立的信息系统，并且组织教授专家对各位同学进行了三个等级的评价.其中：条件属性集C={a1为课外实习，a2四六级通过情况，a3为社会参与（例如：竞赛获奖，担任职务，文体比赛等），a4为专业课成绩平均分，a5为基础课成绩平均分，a6为选修课成绩平均分}，决策属性集D={f为最后得分}.

表1　某学院学生各项指标数据信息表Table 1 A college student index data information table

4.1对表中个属性进行离散化处理

a1，a3，f：（1—优，2—中，3—差）；a2：（1—六级，2—四级，3—未通过）；

a4，a5，a6：（1—＞85，2—70～85，3—＜70）；

4.2信息系统属性约简

根据上面分段，对知识表达系统进行离散化处理，并且消去重复行后得到如下的知识表达系统简化表2.

表2　知识表达系统简化表Table 2　The simplify table of Know ledge expression system

再根据表2建立区分矩阵表3，而区分矩阵是对称矩阵，所以，在计算时只需计算矩阵的一半元素，并且对象自己和自己不区分.

表3　区分矩阵Table 3　Discernibilitymatrix

区分矩阵是一个14×14表格，因为篇幅有限，没有全部列举出来，然后把表格中数据先合取再析取得到区分函数为：

显然，{a1,a2,a3,a4,a5}是指标体系的唯一一个约简，a6为选修课成绩平均分不是关键指标，所以在评价时，不予考虑.

注：当出现多个约简时，任意选择一个约简往下计算即可.

4.3计算指标的客观权重

令C={a1,a2,a3,a4,a5}为新的条件属性，有

则：

可以求得：

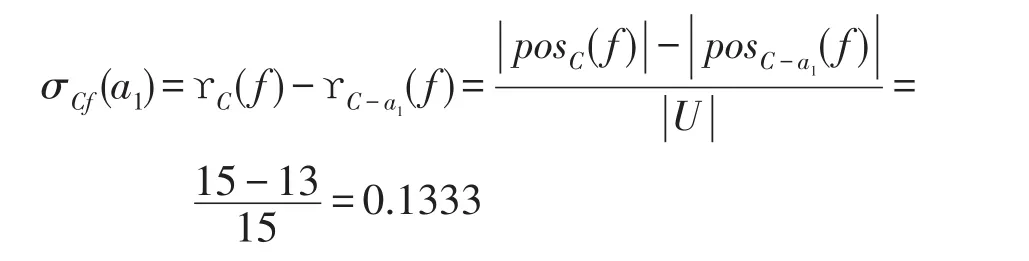
同理可得：

σCf（a2）=0.1333,σCf（a3）=0.2,

σCf（a4）=0.2667,σCf（a5）=0.2

经过归一化处理后，最后各指标权重为：

w1（a3）=w1（a5）=0.2143，w1（a4）=0.2856

4.4计算指标的主观权重

根据查阅相关资料[12]，通过两两比较，建立a1、a2、a3、a4、a5五个指标的1-9标度成对比较阵：

计算矩阵A最大特征值为：λ=5.0204；

最大特征值对应归一化的特征向量为：w2=（0.0663,0.1380,0.0669,0.4547,0.2742）；

因此，权向量（特征向量）可以作为最终决策的依据.

4.5对学生进行综合评价

取α=2,β=1，即在评价时，更偏重客观因素，可得：

为了更好地观察结果，将指标中的定性数据转化成相应的分值，如下：

a1，a3：（优—60，中—40，差—20）；

a2：（六级—60，四级—40，未通过—20）；

由此可由

计算得出表4.

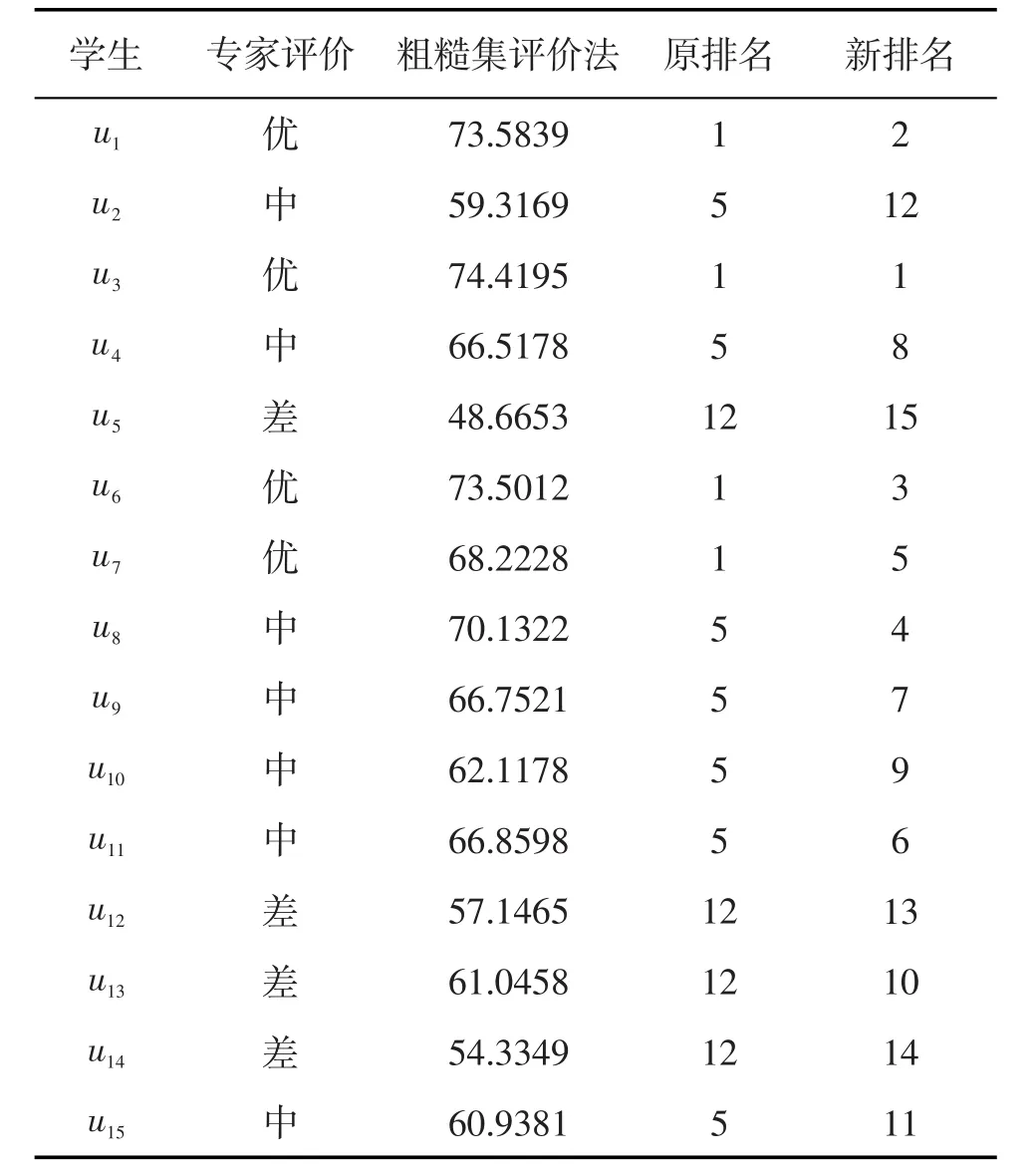
表4　两种评价法结果比较Table 4　Comparison of the resultsabout two kindsof evaluationmethod

5　结论

从表4可以看出，u7、u15与专家评价（即人为主观评价打分）稍有差距，主要原因在于u7虽然专业和基础成绩优秀，但是其他方面较差，而u15与u13几乎一样，但专家给的评价相差很大，其根源在于专家评价给出的结果本身不太准确.所以传统的专家评价法具有太大的主观性，而本文所提出的粗糙集层次分析法在属性约简和权重确定上，既考虑数据自身的特性，同时也考虑专家们的意见，从而得到更为细致准确的结果.

[1]韩中庚.数学建模方法及其应用[M].第二版.北京：高等教育出版社，2009.

[2]司守奎,孙玺菁.数学建模算法与应用[M].北京：国防工业出版社，2011.

[3]李远远,云俊.多属性综合评价指标体系理论综述[J].武汉理工大学学报,2009,31（2）：305-309.

[4]曾文才.模糊综合评判失效的分析于对策[J].系统工程理论方法应用，1995,4（2）：53-59.

[5]卢鹏,吴建乐.基于下近似的粗糙度不等式[J].西南民族大学学报（自然科学版）,2013,39（3）：357-361.

[6]Pawlak Z.Rough Set[J].International Journal of Computer and In⁃formation Science,1982（11）：341-356.

[7]张文修,吴志伟,梁吉业,等.粗糙集理论和方法[M].北京：科学出版社，2001.

[8]郭金玉,张忠彬,孙庆云.层次分析法的研究与应用[J].中国安全科学学报,2008,18（5）：148-153.

[9]王彪,段禅伦,吴昊,等.糊糙集与模糊集的研究及应用[M].北京：电子工业出版社,2008.

[10]Skowron A,Rauszer C.The discernibilitymatricesand functions in information system[C]∥Intelligent Decision Support：Handbook of Applicationsand AdvancesofRough Sets Theory.Dordrecht：Kluw⁃er Academic Publisher,1992：331-362.

[11]左孝凌,李为鑑,刘永才.离散数学[M].上海：上海科学技术文献出版社，1981.

[12]李庆利.高校学生综合评价体系的实证研究[J].经济研究导刊, 2014（25）：222-226.

（编校：许洁）

Application of Rough Set of Analytic Hierarchy Process in the Com prehensive Evaluation of Students

LUPeng1,WU Jianle2
（1.Division ofFoundation Courses,EmeiCampus,Southwest Jiaotong University,Emei,Sichuan 614202,China；2.College ofMathe⁃matics,Southwest Jiaotong University,Chengdu,Sichuan 610031,China）

The rough set theory and analytic hierarchy process（AHP）were introduced in the comprehensive evaluation of student,which can take advantage of rough set theory's particular functions of attribute-reduction and attribute-signifi⁃cance to realize in-depth analysisofdata and ensure objectivity,while AHP isa supplementon the subjective.The com⁃bination of the twomethods can optimize the comprehensive evaluation process.At the same time,rough setof AHP com⁃prehensive evaluation processwasestablished andmethodsofeach step were provided.An examplewasalso given to vali⁃date the feasibility and practicability of themethod.

rough set；analytic hierarchy process；comprehensive evaluation；attribute reduction

O159

A

1671-5365（2015）06-00103-05

2015-01-20修回：2015-03-12

中央高校基本科研业务费专项资金（2682014BR039）

卢鹏（1983-），男，讲师，硕士，研究方向为数学建模理论与方法、粗糙集理论与应用

网络出版时间：2015-03-13 15：10网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20150313.1510.001.html

引用格式：卢鹏，吴建乐.粗糙集层次分析法在学生综合评价中的应用[J].宜宾学院学报,2015,15（6）：103-107.